Ход Рейдемейстера
 |  |  |
| Тип I | Тип II | Тип III |
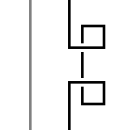 |
| Тип I' |
В математической области теории узлов — ход Райдемейстера это любой из трех локальных ходов на диаграмме связей . Курт Райдемайстер ( 1927 ) и независимо Джеймс Уоддел Александер и Гарланд Бэрд Бриггс ( 1926 ) продемонстрировали, что две диаграммы узлов, принадлежащие одному и тому же узлу, с точностью до планарной изотопии могут быть связаны последовательностью трех движений Райдемайстера.
Каждый ход действует на небольшой области диаграммы и относится к одному из трех типов:
- Скручивайте и раскручивайте в любом направлении.
- Переместите одну петлю полностью поверх другой.
- Переместите веревку полностью над или под пересечением.
Никакая другая часть диаграммы не участвует в картине хода, и плоская изотопия может исказить картину. Нумерация типов ходов соответствует количеству задействованных цепочек, например, ход типа II действует на двух цепочках диаграммы.
Одним из важных контекстов, в которых появляются движения Райдемейстера, является определение инвариантов узлов . Инвариант определяется путем демонстрации свойства диаграммы узла, которое не меняется при применении любого из движений Райдемейстера. Таким способом можно определить многие важные инварианты, включая полином Джонса .
Движение типа I — единственное движение, которое влияет на корчание диаграммы. Ход типа III — единственный, который не меняет номер пересечения диаграммы.
В таких приложениях, как исчисление Кирби , в которых желаемый класс эквивалентности диаграмм узлов является не узлом, а структурированной связью , необходимо заменить перемещение типа I на перемещение «модифицированного типа I» (тип I'), состоящее из двух типов: Я двигаюсь противоположного смысла. Движение типа I не влияет ни на структуру звена, ни на извилистость всей диаграммы узла.
Трэйс (1983) показал, что две диаграммы узлов для одного и того же узла связаны только с использованием движений типа II и III тогда и только тогда, когда они имеют одинаковое число изгибов и намоток . Более того, совместная работа Эстлунда (2001) , Мантурова (2004) и Хагге (2006) показывает, что для каждого типа узла существует пара диаграмм узлов, так что каждая последовательность движений Райдемейстера, переводящая один в другой, должна использовать все три типа. ходов. Александр Кауард продемонстрировал, что для диаграмм связей, представляющих эквивалентные ссылки, существует последовательность ходов, упорядоченная по типам: сначала ходы типа I, затем ходы типа II, типа III, а затем типа II. Ходы перед ходами типа III увеличивают количество пересечений, а ходы после ходов уменьшают количество пересечений.
Кауард и Лакенби (2014) доказали существование верхней границы экспоненциальной башни (в зависимости от числа пересечений) количества ходов Райдемейстера, необходимых для перехода между двумя диаграммами одного и того же звена. Подробно, пусть быть суммой чисел пересечений двух диаграмм, то верхняя граница равна где высота башни с (с одним вверху) есть
Лакенби (2015) доказал существование полиномиальной верхней границы (в зависимости от числа пересечений) количества ходов Райдемейстера, необходимых для изменения диаграммы узла на стандартный узел. Подробно, для любой такой диаграммы с пересечений, верхняя граница равна .
Хаяши (2005) доказал, что существует также верхняя граница, зависящая от числа пересечений, количества ходов Райдемейстера, необходимых для разделения ссылки .
Ссылки
[ редактировать ] СМИ, связанные с переездом Райдемайстера, на Викискладе?
СМИ, связанные с переездом Райдемайстера, на Викискладе? - Александр, Джеймс В.; Бриггс, Гарланд Б. (1926), «О типах кривых с узлами», Annals of Mathematics , 28 (1/4): 562–586, doi : 10.2307/1968399 , JSTOR 1968399 , MR 1502807
- Трус, Александр; Лакенби, Марк (2014), «Верхняя граница движений Райдемейстера» , American Journal of Mathematics , 136 (4): 1023–1066, arXiv : 1104.1882 , doi : 10.1353/ajm.2014.0027 , MR 3245186 , S2CID 55882290
- Галатоло, Стефано (1999), «О проблеме эффективной теории узлов» , Atti Accad. Нат. Линчеи Кл. Науч. Мэтт. Естественный. Возвращаться Линсианцы (9) Мат. Прил. , 9 (4): 299–306, МР 1722788
- Хагге, Тобиас (2006), «Каждое движение Райдемейстера необходимо для каждого типа узла», Proc. амер. Математика. Соц. , 134 (1): 295–301, doi : 10.1090/S0002-9939-05-07935-9 , MR 2170571
- Хасс, Джоэл ; Лагариас, Джеффри К. (2001), «Количество ходов Райдемейстера, необходимое для развязывания узлов», Журнал Американского математического общества , 14 (2): 399–428, arXiv : math/9807012 , doi : 10.1090/S0894-0347- 01-00358-7 , МР 1815217 , С2КИД 15654705
- Хаяши, Чуичиро (2005), «Количество ходов Райдемайстера для разделения ссылки», Mathematische Annalen , 332 (2): 239–252, doi : 10.1007/s00208-004-0599-x , MR 2178061 , S2CID 119728321
- Лакенби, Марк (2015), «Полиномиальная верхняя граница движений Райдемайстера», Annals of Mathematics , Second Series, 182 (2): 491–564, arXiv : 1302.0180 , doi : 10.4007/annals.2015.182.2.3 , MR 3418524 , S2CID 119662237
- Мантуров, Василий Олегович (2004), Теория узлов , Бока-Ратон, Флорида: Chapman & Hall/CRC, doi : 10.1201/9780203402849 , ISBN 0-415-31001-6 , МР 2068425
- Эстлунд, Олоф-Петтер (2001), «Инварианты диаграмм узлов и отношения между движениями Райдемейстера», J. Knot Theory Ramifications , 10 (8): 1215–1227, arXiv : math/0005108 , doi : 10.1142/S0218216501001402 , MR 187122 6 , S2CID 119177881
- Райдемайстер, Курт (1927), «Элементарное обоснование теории узлов», кафедра математики Univ. Гамбург , 5 (1): 24–32, doi : 10.1007/BF02952507 , MR 3069462 , S2CID 120149796
- Трейс, Брюс (1983), «О движениях Райдемейстера классического узла», Proceedings of the American Mathematical Society , 89 (4): 722–724, doi : 10.2307/2044613 , JSTOR 2044613 , MR 0719004





