Фрактальный пейзаж
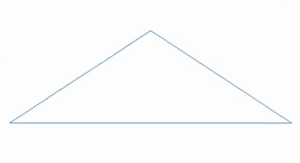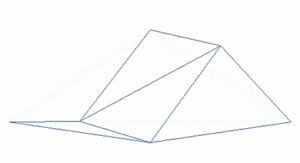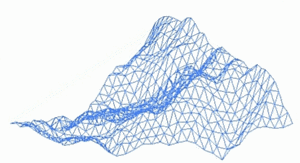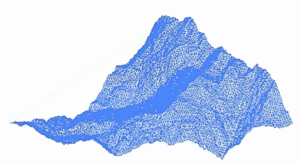
Фрактальный ландшафт или фрактальная поверхность создается с использованием стохастического алгоритма, предназначенного для создания фрактального поведения, имитирующего внешний вид естественной местности . Другими словами, поверхность, полученная в результате этой процедуры, является не детерминированной, а скорее случайной поверхностью, проявляющей фрактальное поведение. [1]
Многие природные явления демонстрируют некоторую форму статистического самоподобия , которую можно смоделировать с помощью фрактальных поверхностей . [2] Более того, различия в текстуре поверхности дают важные визуальные подсказки об ориентации и наклонах поверхностей, а использование почти самоподобных фрактальных узоров может помочь создать естественные визуальные эффекты. [3] Моделирование шероховатой поверхности Земли посредством дробного броуновского движения было впервые предложено Бенуа Мандельбротом . [4]
Поскольку предполагаемым результатом процесса является создание ландшафта, а не математической функции, к таким ландшафтам часто применяются процессы, которые могут повлиять на стационарность и даже общее фрактальное поведение такой поверхности в интересах создания более убедительной модели. пейзаж.
По мнению Р. Р. Ширера , создание естественно выглядящих поверхностей и пейзажей стало важным поворотным моментом в истории искусства, когда различие между геометрическими, созданными компьютером изображениями и естественным, искусственным искусством стало размытым. [5] Первое использование фрактального пейзажа в кино было в 1982 году в фильме « Звездный путь 2: Гнев Хана» . Лорен Карпентер усовершенствовала технику Мандельброта для создания инопланетного пейзажа. [6]
Поведение природных ландшафтов
[ редактировать ]


Вопрос о том, ведут ли природные ландшафты в целом фрактальный характер, был предметом некоторых исследований. Технически говоря, любая поверхность в трехмерном пространстве имеет топологическую размерность 2, и, следовательно, любая фрактальная поверхность в трехмерном пространстве имеет хаусдорфову размерность от 2 до 3. [7] Однако реальные ландшафты ведут себя по-разному в разных масштабах. Это означает, что попытка вычислить «общую» фрактальную размерность реального ландшафта может привести к получению показателей отрицательной фрактальной размерности или фрактальной размерности выше 3. В частности, многие исследования природных явлений, даже тех, которые обычно считаются демонстрирующими фрактальное поведение, , не делайте этого более чем на несколько порядков. Например, исследование Ричардсоном западного побережья Великобритании показало фрактальное поведение береговой линии всего на два порядка величины. [8] В общем, нет оснований предполагать, что геологические процессы, формирующие ландшафт в больших масштабах (например, тектоника плит ), демонстрируют такое же математическое поведение, как те, которые формируют ландшафт в меньших масштабах (например, ползучесть почвы ).
Реальные ландшафты также имеют различное статистическое поведение от места к месту, поэтому, например, песчаные пляжи не обладают такими же фрактальными свойствами, как горные хребты. Однако фрактальная функция статистически стационарна, а это означает, что ее основные статистические свойства везде одинаковы. Таким образом, любой реальный подход к моделированию ландшафтов требует способности пространственно модулировать фрактальное поведение. Кроме того, в реальных ландшафтах очень мало естественных минимумов (большинство из них — озера), тогда как фрактальная функция в среднем имеет столько же минимумов, сколько и максимумов. Реальные ландшафты также имеют особенности, обусловленные течением воды и льда по их поверхности, которые простые фракталы не могут смоделировать. [9]
Именно по этим соображениям простые фрактальные функции часто непригодны для моделирования ландшафтов. Более сложные методы (известные как «мультифрактальные» методы) используют разные фрактальные измерения для разных масштабов и, таким образом, могут лучше моделировать поведение частотного спектра реальных ландшафтов. [10]
Генерация фрактальных ландшафтов
[ редактировать ]Способ создания такого ландшафта — использовать алгоритм случайного смещения средней точки , в котором квадрат делится на четыре меньших равных квадрата, а центральная точка смещается по вертикали на некоторую случайную величину. Процесс повторяется на четырех новых квадратах и так далее, пока не будет достигнут желаемый уровень детализации . Существует множество фрактальных процедур (таких как объединение нескольких октав симплексного шума ), способных создавать данные о местности, однако термин «фрактальный ландшафт» со временем стал более общим.
Фрактальные растения
[ редактировать ]Фрактальные растения можно генерировать процедурно с использованием L-систем в компьютерных сценах. [11]
См. также
[ редактировать ]- Броуновская поверхность
- Брайс
- Алгоритм ромба-квадрата
- Программное обеспечение для генерации фракталов
- Гром
- Карта высот
- Аутерра
- Генератор пейзажей
- Терраген
- Октри
- Четырехдерево
Примечания
[ редактировать ]- ^ «Фрактальная геометрия природы» .
- ^ Достижения в области мультимедийного моделирования: 13-я Международная конференция по мультимедийному моделированию , Тат-Джен Чам, 2007 г. ISBN 3-540-69428-5 страница [1]
- ^ Восприятие симметрии человека и его вычислительный анализ Кристофера В. Тайлера, 2002 г. ISBN 0-8058-4395-7 страницы 173–177 [2]
- ^ Динамика фрактальных поверхностей, авторы Семьи Ферейдун и Тамас Вичек, 1991 г. ISBN 981-02-0720-4 стр. 45 [3]
- ^ Ронда Роланд Ширер «Переосмысление образов и метафор» в Языки мозга» книге Альберта М. Галабурды « , 2002 г. ISBN 0-674-00772-7 страниц 351–359 [4]
- ^ Бриггс, Джон (1992). Фракталы: закономерности хаоса: новая эстетика искусства, науки и природы . Саймон и Шустер. п. 84. ИСБН 978-0671742171 . Проверено 15 июня 2014 г.
- ^ Льюис
- ^ Ричардсон
- ^ Кен Масгрейв, 1993
- ^ Йост ван Лавик из Pabst et al.
- ^ де ла Ре, Армандо; Абад, Франциско; Камахорт, Эмилио; Хуан, MC (2009). «Инструменты для процедурной генерации растений в виртуальных сценах» (PDF) . Вычислительная наука – ICCS 2009 . Конспекты лекций по информатике. Том. 5545. стр. 801–810. дои : 10.1007/978-3-642-01973-9_89 . ISBN 978-3-642-01972-2 . S2CID 33892094 .
Ссылки
[ редактировать ]- Льюис, Дж. П. «Подходит ли фрактальная модель для местности?» (PDF) .
- Ричардсон, LF (1961). «Проблема непрерывности». Ежегодник общих систем. 6 : 139–187.
- ван Лавик ван Пабст, Йост; Йенсе, Ганс (2001). «Динамическое создание ландшафта на основе мультифрактальных методов» (PDF) . Архивировано из оригинала (PDF) 24 июля 2011 г.
- Масгрейв, Кен (1993). «Методы реалистичного изображения ландшафта» (PDF) .
Внешние ссылки
[ редактировать ]- «Мир Интернета» , Кен Перлин, 1998; Java-апплет, показывающий сферу с сгенерированным ландшафтом.