XaoS
 | |
| Оригинальный автор(ы) | Ян Губичка, Томас Марш |
|---|---|
| Разработчик(и) | Участники XaoS |
| Стабильная версия | 4.3.2 / 18 января 2024 г |
| Репозиторий | |
| Написано в | С , С++ |
| Операционная система | Кросс-платформенный |
| Доступно в | 16 языков |
Список языков | |
| Тип | Программное обеспечение для генерации фракталов |
| Лицензия | лицензия GPL |
| Веб-сайт | XAOS-проект |
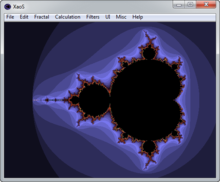
XaoS — это интерактивная программа фрактального масштабирования . Это позволяет пользователю непрерывно увеличивать или уменьшать масштаб фрактала в режиме реального времени.
XaoS распространяется под лицензией GPL . Программа является кроссплатформенной и доступна для множества операционных систем , включая Linux , Windows , Mac OS X , BeOS и другие. Недавно стала доступна автономная веб-версия XaoS, опубликованная на сайте xaos.
XaoS может отображать множество Мандельброта (степень 2, 3, 4, 5 и 6), фрактал Окто, три типа фракталов Барнсли , фрактал Ньютона (порядок 3 и 4), фрактал Феникса и Магнит (1 и 2). XaoS может отображать наборы Джулии из выбранных фрактальных частей. Xaos также позволяет пользователям вводить собственные формулы.
Более ранние версии XaoS способны отображать фракталы в виде ASCII-изображений с помощью AAlib , что в сочетании со свободно доступными инструментами GNU позволяет запускать его практически где угодно. В более новых версиях используется кроссплатформенная библиотека Qt .
Включены интерактивная помощь и анимированное введение в фракталы. Введение состоит из десяти глав, посвященных различным формулам, представленным в программном обеспечении, и их функциям.
Алгоритм сопла [ править ]
Изначально XaoS был просто «плохо написанной» программой просмотра Мандельброта, [1] пока Ян Губичка не добавил эффективное масштабирование, используя метод, который иногда называют алгоритмом XaoS или алгоритмом Губички.
В то время фильмы с фрактальным зумом создавались путем полного пересчета каждого кадра, хотя, естественно, большая часть их площади была общей. Это сделало интерактивное масштабирование невозможным без очень мощных компьютеров. [2] Более того, если для сглаживания не используется еще большая обработка , пересчет каждого кадра приводит к эффекту «мерцания», когда небольшие яркие области попадают, а затем исчезают между пикселями. [3]
Тем не менее, разрешение пользователю масштабировать изображение, а не прыгать, как во Fractint , казалось наиболее естественным способом взаимодействия с фракталами. Чтобы создать интерактивное масштабирование, Губичке нужно было найти способ сохранить уже сделанные расчеты. Для сохранения каждого когда-либо рассчитанного пикселя потребовалось бы слишком много памяти, поэтому алгоритм Губички сохраняет только предыдущий кадр, и вместо того, чтобы запоминать местоположение каждого пикселя, он может выровнять их по строкам и столбцам и вместо этого запоминать их.
Самой сложной частью алгоритма XaoS был выбор, какие сохраненные строки и столбцы где рисовать. Неправильное выполнение этого действия приводит к искажению изображений, однако, чтобы оно принесло пользу, оно должно быть сделано быстро. После того, как было опробовано несколько различных эвристик, в конечном итоге проблема была решена как задача оптимизации.
Остальные строки и столбцы окрашены в тот же цвет, что и ближайшая строка/столбец, и вычисляются заново, когда у ЦП появляется время для этого. Это тщательный баланс между сохранением масштаба и повышением уровня детализации. Вычислению областей, к которым изображение приближается, уделяется более высокий приоритет, поскольку они будут на экране дольше всего и, скорее всего, именно туда в любом случае смотрит пользователь. При уменьшении масштаба происходит обратный процесс, и приоритет оказывается на краях. [3]
Алгоритм Губички также может применяться для увеличения других изображений, где рассчитываются пиксели, и использовался в другом программном обеспечении, таком как rtzme («Математический механизм масштабирования в реальном времени»), программа построения графиков сложных функций, [4] и другие фрактальные зумеры.
Ссылки [ править ]
- ^ Справочная страница XaoS
- ^ CS and Dance (PDF) , заархивировано из оригинала 20 декабря 2005 г.
- ^ Jump up to: Перейти обратно: а б Губичка, Ян (1997), Алгоритмы XaoS , заархивировано из оригинала 28 марта 2014 г.
- ^ Визуализации на сложной плоскости , заархивировано из оригинала 17 октября 2006 г.
