Инверсия (музыка)

${#(set-global-staff-size 16) \new PianoStaff << \новый персонал << \ относительно с'' { \set Score.currentBarNumber = #21 \set Score.proportionalNotationDuration = #(ly:make-moment 1/8) \бар "" \clef treble \key d \minor \time 3/4 \once \override TextScript.script-priority = #-100 a4~^\mordent^\markup {\sharp } a16 g! откормленный \override NoteHead.color = #red \stemUp e8 e' d cis bd \override NoteHead.color = #black cis16 } >> \новый персонал << \ключ бас \клавиша ре \минор \тайм 3/4 \новый голос \relative c' { \override NoteHead.color = #red a8 a, b cis db \override NoteHead.color = #black cis16 a gis a f'4-. d\trill a'8 } \новый голос \relative c' { \stemUp \override NoteHead.color = #red a4 rr } >> >> }$

Пример мелодической инверсии из фуги ре минор из И. С. Баха , «Хорошо темперированного клавира» книга 1. ^[1] Хотя они начинаются с разных тонов (A и E), вторая выделенная мелодия представляет собой перевернутую версию первой выделенной мелодии. То есть, когда первый идет вверх , второй опускается на такое же количество диатонических ступеней (с некоторым хроматическим изменением); и когда первый опускается , второй поднимается на такое же количество ступенек.

В теории музыки инверсия — это перестановка верхних элементов интервала, аккорда, мелодии или группы контрапунктических линий музыки. ^[2] В каждом из этих случаев «инверсия» имеет отдельное, но связанное значение. Понятие инверсии также играет важную роль в теории музыкальных множеств .

Интервалы

Интервал так инвертируется путем повышения или понижения любой из нот на одну или несколько октав, что более высокая нота становится нижней и наоборот. Например, инверсия интервала, состоящего из ноты «до» с «ми» над ним (третий такт ниже), представляет собой «ми» с «до» над ним. или оба могут быть перемещены.

${\override Score.TimeSignature#'stencil = ##f\override Score.SpacingSpanner.strict-note-spacing = ##t\set Score.proportionalNotationDuration = #(ly:make-moment 1/4)\новый персонал << \ключ скрипичный \время 4/4 \новый голос \relative c' { \stemUp c2 c' c, c' c, c' c, c' } \новый голос \relative c' { \stemDown c2 cddeeff } \addlyrics { "P1" -- "P8" "M2" -- "m7" "M3" -- "m6" "P4" -- "P5" }>>}$

Номер интервала при инверсии
Унисон	↔	Октава
Второй	↔	Седьмой
Третий	↔	Шестой
Четвертый	↔	Пятый

Интервальное качество при инверсии
Идеальный	↔	Идеальный
Главный	↔	Незначительный
Дополненный	↔	Уменьшенный
Острый	↔	Могила

В таблицах справа показаны изменения качества интервала и номера интервала при инверсии. Таким образом, совершенные интервалы остаются совершенными, большие становятся второстепенными и наоборот, а увеличенные становятся уменьшенными и наоборот. (Двукратно уменьшенные интервалы становятся вдвое увеличенными, и наоборот.).

Традиционные интервальные числа в сумме дают девять: секунды становятся седьмыми и наоборот, терции становятся шестыми и наоборот и так далее. Таким образом, чистая кварта становится идеальной квинтой, увеличенная кварта становится уменьшенной квинтой, а простой интервал (то есть тот, который уже октавы) и его инверсия, сложенные вместе, равны октаве. См. также дополнение (музыка) .

Аккорды

${\override Score.SpacingSpanner.strict-note-spacing = ##t\set Score.proportionalNotationDuration = #(ly:make-moment 1/8) \new PianoStaff << \новый персонал << \новый голос \relative c' { \ключ скрипичный \время 4/4 \once \override NoteHead.color = #red <c g'>4 <c f> \once \override NoteHead.color = #red <c e> c \stemDown c4 b \once \override NoteHead.color = #red c2 } \addlyrics { К Его небесам -- мой приятель -- врата туза. } \новый голос \relative c' { s1 \stemUp d4. d8 \once \override NoteHead.color = #red c2 } >> \новый персонал << \новый голос \relative c, { \ключ бас \время 4/4 \once \override NoteHead.color = #red <e g'>4 <f a'> \once \override NoteHead.color = #red <g g'> <a e'> <f a'> \stemDown g \once \override NoteHead.color = #red c2 } \новый голос \relative c' { s1 s4 \stemUp g8 f \once \override NoteHead.color = #red e2 } \цифры { <6>2 <6 4>2 <6 5>4. <7>8 } >> >> }$

Заключительная фраза гимна « Растингтон» английского композитора Хьюберта Парри (1897 г.): ^[3] показаны все три позиции аккорда до мажор. ^[а] . на рисунке ниже. см Описание цифровых символов

Инверсия аккорда описывает отношение его самых низких нот к другим нотам аккорда. Например, трезвучие до мажор содержит тона C, E и G; его инверсия определяется тем, какой из этих тонов является самой низкой нотой (или басовой нотой ) в аккорде.

Термин «инверсия» часто категорически относится к различным возможностям, хотя он также может быть ограничен только теми аккордами, в которых самая низкая нота не является также основной нотой аккорда. В текстах, которые следуют этому ограничению, вместо этого может использоваться термин «позиция» , чтобы обозначить все возможности как категорию.

Основное положение и перевернутые аккорды

Аккорд находится в основной позиции, если его основной тон является самой нижней нотой. Иногда его называют родительским аккордом его инверсий. Например, основой до-мажорного трезвучия является C, поэтому до-мажорное трезвучие будет находиться в основной позиции, если C является самой нижней нотой, а ее третья и пятая (E и G соответственно) находятся над ней – или, случай, вообще не звучат.

Следующие трезвучия до-мажор находятся в основной позиции, поскольку самая нижняя нота является основной. Перестановка нот над басом в разные октавы (здесь нота ми) и удвоение нот (здесь соль) называется звонкостью – первая звонкость — закрытая , вторая — открытая .

${\override Score.TimeSignature#'stencil = ##f\override Score.SpacingSpanner.strict-note-spacing = ##t\set Score.proportionalNotationDuration = #(ly:make-moment 1/4)\время 4/4 \относительный с' { <ce g>1^\markup { \column { "Корневая" "позиция" } } <c g' e' g>^\markup { \column { "Корневая" "позиция" } } }}$

В перевернутом аккорде основной тон не является самой нижней нотой. Обращения нумеруются в том порядке, в котором их самые низкие ноты появляются в близком корневом аккорде (снизу вверх).

${\override Score.TimeSignature#'stencil = ##f\override Score.SpacingSpanner.strict-note-spacing = ##t\set Score.proportionalNotationDuration = #(ly:make-moment 1/4)\время 4/4 \относительный с' { <ce g>1^\markup { \column { "Корневая" "позиция" } } <eg c>1^\markup { \column { "Первая" "инверсия" } } <gc e>1^\markup { \column { "Вторая" "инверсия" } } }}$

Как показано выше, трезвучие до мажор (или любой аккорд с тремя нотами) имеет две инверсии:

В первой инверсии самая нижняя нота — это E — третья трезвучия — над ней расположена квинта и основной тон (теперь основной тон сдвинут на октаву выше), образуя интервалы минорной терции и минорной шестой над перевернутой. бас ми соответственно.
Во второй инверсии самой низкой нотой является соль — пятая часть трезвучия — с основным тоном и третьей над ней (обе снова сдвинуты на октаву выше), образуя четвертую и шестую над (перевернутым) басом соль соответственно. .

Аккорды с четырьмя нотами (например, септаккорды ) работают аналогичным образом, за исключением того, что у них есть три обращения вместо двух. Три обращения доминантного септаккорда G :

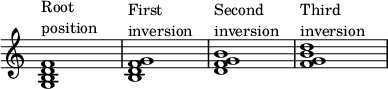
${\override Score.TimeSignature#'stencil = ##f\override Score.SpacingSpanner.strict-note-spacing = ##t\set Score.proportionalNotationDuration = #(ly:make-moment 1/4)\время 4/4 \относительный с' { <gbd f>1^\markup { \column { "Корневая" "позиция" } } <bdf g>1^\markup { \column { "Первая" "инверсия" } } <dfg b>1^\markup { \column { "Вторая" "инверсия" } } <fgb d>1^\markup { \column { "Третья" "инверсия" } } }}$

Обозначение положения корня и инверсий

Фигурный бас

Общие условные обозначения фигурного баса
Триады
Инверсия	Интервалы выше баса	Символ	Пример
Корневая позиция	⁵ ₃	Никто	${ \override Score.TimeSignature #'stencil = ##f \new PianoStaff << \новый персонал << \относительный с' { \ключ скрипичный \время 3/4 <eg c>4 <c g' c> <ce g> } >> \новый персонал << \ относительно с { \ключ бас \время 3/4 с4 например } \цифры { < _ >4 <6> <6 4> } >> >> }$
1-я инверсия	⁶ ₃	⁶
2-я инверсия	⁶ ₄	⁶ ₄
Седьмые аккорды
Инверсия	Интервалы выше баса	Символ	Пример
Корневая позиция	7 5 3	⁷	${ \override Score.TimeSignature #'stencil = ##f \new PianoStaff << \новый персонал << \относительный с' { \ключ скрипичный \время 4/4 <bd f>4 <g d' f> <b f' g > <bd g> } >> \новый персонал << \ относительно с { \ключ бас \время 4/4 g4 бдф } \цифры { <7>4 <6 5> <4 3> <4 2> } >> >> }$
1-я инверсия	6 5 3	⁶ ₅
2-я инверсия	6 4 3	⁴ ₃
3-я инверсия	6 4 2	⁴ ₂ или ²

Фигурный бас — это обозначение, в котором обращения аккордов обозначаются арабскими цифрами ( цифрами ) над или под басовыми нотами , что указывает на гармоническую последовательность . Каждая цифра выражает интервал, возникающий из голосов над ней (обычно предполагая октавную эквивалентность ). Например, в триаде C–E–G с основной позицией интервалы над басовой нотой C составляют третью и квинту, что дает цифры ⁵
₃ . Если бы эта триада находилась в первой инверсии (например, E–G–C), то фигура ⁶
₃ , поскольку интервалы в треть и шестую появляются над басовой нотой E.

При использовании фигурного баса существуют определенные общепринятые сокращения. Например, триады корневых позиций появляются без символов (т. ⁵
₃ понятен), а триады первой инверсии обычно обозначаются просто ⁶, скорее, чем ⁶
₃ . В таблице справа показаны эти соглашения.

Фигурные басовые цифры обозначают отдельные интервалы в аккорде только в том случае, если они относятся к басовой ноте. В них нет ссылки на тональность прогрессии (в отличие от римско-цифрового гармонического анализа ), они не выражают сами интервалы между парами верхних голосов - например, в трезвучии C–E–G фигурный бас не означает интервальное соотношение между E – G, и они не выражают ноты в верхних голосах, которые удваивают басовую ноту или находятся в унисон с ней.

Однако в теории музыки цифры часто используются сами по себе (без баса) просто для обозначения обращения аккорда. Это является основой для приведенных выше терминов, таких как « ⁶
₄ аккорда » для второго инверсионного трезвучия. Точно так же в гармоническом анализе термин I ⁶ относится к тоническому трезвучию в первом обращении.

Нотная запись популярной музыки

Обозначение обращения аккорда, часто используемое в популярной музыке, заключается в написании названия аккорда, за которым следует косая черта, а затем название басовой ноты. ^[4] Это называется слэш-аккорд . Например, аккорд до мажор в первом обращении (т. е. с E в басу) будет обозначаться как «C/E». Эта запись работает, даже если нота, отсутствующая в трезвучии, является басом; например, Ф/Г ^[5] это способ обозначить особый подход к озвучиванию причуды ⁹ аккорд (G–F–A–C). Это сильно отличается от аналитических обозначений функции ; обозначение «IV/V» представляет собой субдоминанту доминанты например , .

Строчные буквы

Строчные буквы могут быть помещены после символа аккорда, чтобы указать положение основного тона или инверсию. ^[6]^{[ нужна страница ]} Следовательно, в тональности до мажор аккорд до мажор в первом обращении может быть обозначен как Ib , что указывает на аккорд I, первое обращение . (Реже указывается корень аккорда, за которым следует строчная буква: Cb ). Если буква не добавлена, предполагается, что аккорд находится в инверсии основного корня, как если бы буква была вставлена .

История

В » Жана-Филиппа Рамо ( «Трактате о гармонии 1722 г.) аккорды в различных инверсиях считаются функционально эквивалентными, и он считается первым человеком, осознавшим их основное сходство. ^[7]^[8] Ранее теоретики говорили о разных интервалах, используя альтернативные описания, такие как regola delle terze e seste («правило шестых и третей»). Это требовало разрешения несовершенных созвучий в совершенные и не предполагало, например, сходства между ⁶
₄ и ⁵
₃ аккорда.

Контрапункт

${ \new PianoStaff << \новый персонал << \относительный с' { \clef treble \key a \minor \time 4/4 \set Score.currentBarNumber = #18 \бар "" r16 \override NoteHead.color = #red eacbe, b' d \override NoteHead.color = #blue c8 a gis e \override NoteHead.color = #black а16 } >> \новый персонал << \относительный с' { \ключ бас \клавиш ля \минор \тайм 4/4 \override NoteHead.color = #blue c8 a gis e \override NoteHead.color = #black a16 \override NoteHead.color = #red eacbe, b' d \override NoteHead.color = #black c } >> >> }$

Пример контрапунктической инверсии в одном такте Инвенции И.С. Баха № 13 ля минор, BWV 784 .

При контрапунктической инверсии две мелодии , ранее один раз сопровождавшие друг друга, снова сопровождают друг друга, но уже той мелодией, которая была в высоком голосе, теперь в низком, и наоборот. Действие по изменению голосов называется текстурной инверсией . Это называется двойным контрапунктом , когда участвуют два голоса, и тройным контрапунктом , когда участвуют три. Инверсия в двухчастном обратимом контрапункте также известна как rivolgimento . ^[9]

Обратимый контрапункт

Темы , которые можно развивать таким образом, не нарушая правил контрапункта, называются обратимыми контрапунктами . Обратный контрапункт может возникать на различных интервалах, обычно на октаве , реже на десятой или двенадцатой . Чтобы вычислить интервал инверсии, ^{[ нужны разъяснения ]} сложите интервалы, на которые переместился каждый голос, и вычтите единицу. Например: если мотив A в высоком голосе смещается на шестую вниз, а мотив B в низком голосе поднимается на квинту таким образом, что A и B поменялись регистрами, то они находятся в двойном контрапункте на уровне десятый (6+5 – 1=10).

В » И. С. Баха первый «Искусстве фуги канон находится на октаве, второй канон на десятой, третий канон на двенадцатой, а четвертый канон в увеличении и противоположном движении. Другие образцы можно найти в фугах соль минор и си ♭ мажор [внешние фильмы Shockwave] из книги И. С. Баха « Хорошо темперированный клавир» , книга 2, обе из которых содержат обратимый контрапункт в октаве, десятой и двенадцатой октаве.

Примеры

Например, в клавишной прелюдии ля мажор И. С. Баха из «Хорошо темперированного клавира» , книга 1, следующий отрывок из тактов 9–18 включает две строки, по одной в каждой руке:

Прелюдия Баха ля ♭ из тактов 9–18 WTC1.

Когда этот отрывок возвращается в тактах 25–35, эти строки меняются местами:

Прелюдия Баха ля ♭ из тактов 25–36 WTC1.

И.С. Баха Трехголосная инвенция фа минор , BWV 795, предполагает исследование сочетания трех тем. Два из них объявляются в первых двух тактах. Третья идея присоединяется к ним в тактах 3–4. Когда этот отрывок повторяется несколькими тактами позже в тактах 7–9, три части меняются местами:

Трехголосная инвенция Баха (Симфония) фа минор BWV 795, такты 1–9.

Далее в произведении исследуются четыре из шести возможных вариантов того, как эти три строки могут быть объединены в контрапункте.

Один из наиболее ярких примеров обратного контрапункта – финал Моцарта » Симфонии «Юпитер . Здесь одновременно прослушивается не менее пяти тем:

Симфония Моцарта № 41, финал, такты 389–396.

Весь отрывок завершает симфонию ярким оркестровым сочинением. По словам Тома Сервиса :

Сочинение Моцарта финала Симфонии «Юпитер» представляет собой палимпсест не только его собственной, но и истории музыки. В качестве музыкального достижения его наиболее очевидным предшественником на самом деле является фугальный финал его струнного квартета соль мажор К. 387 , но этот симфонический финал превосходит даже эту пьесу по своему масштабу и амбициям. Если история первой части этой оперной мелодии призвана превратить инстинктивные эмоции в контрапунктический опыт, то финал делает прямо противоположное, превращая самые сложные искусства композиционного мастерства в чистые, волнующие чувства. Его модели у Михаэля и Йозефа Гайдна неоспоримы, но Моцарт одновременно отдает им дань уважения – и превосходит их. Вот это я называю настоящей оригинальностью. ^[10]

Мелодии

${#(set-global-staff-size 18)\set Score.currentBarNumber = #1\бар ""\key g \major \time 6/8 \ относительно с'' { \ключ скрипичный g8 a16 g fis g a8 b16 ага b8 agd c'4 b8 аг фис e'4} }$

${#(set-global-staff-size 18)\set Score.currentBarNumber = #28\бар ""\key g \major \time 6/8\ относительно с { \ключ бас d8 c16 ded c8 b16 cdc b8 cdga,4 b8 cde fis,4} }$

Две строки из фуги соль мажор из » И. С. Баха , «Хорошо темперированного клавира книга 1. Самый низкий голос в мм. 28–30 — инверсия вступительной мелодии в мм. 1–3.

Мелодия инвертируется мелодии на противоположный путем переворачивания ее «вверх ногами», меняя контур . Например, если исходная мелодия имеет восходящую мажорную треть , то в перевернутой мелодии есть нисходящая мажорная треть (или, особенно в тональной музыке, возможно, нисходящая минорная треть ).

Согласно Гарвардскому музыкальному словарю , «Интервалы между последовательными тонами могут оставаться точными или, что чаще в тональной музыке, они могут быть эквивалентами в диатонической гамме . Следовательно, c'–d–e' может стать c'–b– a (где первый спуск происходит на полутон, а не на целый тон) вместо c' – b ♭ –a ♭ ». ^[11] Более того, инверсия может начинаться с той же высоты, что и исходная мелодия, но это не обязательно, как показано в примере справа.

Двенадцатитональная музыка

В двенадцатитоновой технике инверсия тонового ряда является одной из четырех ее традиционных перестановок (остальные — это простая форма , ретроградная и ретроградная инверсия ). Эти четыре перестановки (обозначенные как « простая», «ретроградная », « инверсия» и инверсия «ретроградная » ) для тонового ряда, используемого в Арнольда Шенберга «Вариациях для оркестра » , соч. 31 показаны ниже.

${\override Score.TimeSignature#'stencil = ##f\override Score.SpacingSpanner.strict-note-spacing = ##t \set Score.proportionalNotationDuration = #(ly:make-moment 3/1)\новая группа персонала << \новый персонал \ относительно с'' { \время 12/1 bes1^\markup { P } e, fis dis fad cis g aes bc c^\markup { R } b aes g cis daf dis fis e bes' } \новый персонал { \ относительно с'' { bes1^\markup { I } edf dis b fis g cis ca aes aes^\markup {RI } ac cis g fis b dis fde bis } }>> }$

В теории множеств обратную операцию иногда обозначают как $T_{n}I$ , где $I$ означает «инвертировать» и $T_{n}$ означает «транспонировать на некоторый интервал» $n$ "измеряется в количестве полутонов . Таким образом, инверсия представляет собой комбинацию инверсии с последующим транспонированием . Применить операцию инверсии $I$ , вы вычитаете класс высоты тона в целочисленной записи из 12 (по соглашению инверсия происходит вокруг класса тона 0). Затем применяем операцию транспонирования $T_{n}$ добавив $n$ . Например, чтобы вычислить $T_{5}I(3)$ , сначала вычтите 3 из 12 (получится 9), а затем прибавьте 5 (получится 14, что эквивалентно 2). Таким образом, $T_{5}I(3)=2$ . ^[12] Чтобы инвертировать набор тонов, просто инвертируйте каждый тон в наборе по очереди. ^[13]

Инверсионная эквивалентность и симметрия

Теория множеств

В теории множеств инверсионная эквивалентность — это концепция, согласно которой интервалы , аккорды и другие наборы высот одинаковы при инвертировании. ^{[ нужна ссылка ]} Это похоже на энгармоническую эквивалентность , октавную эквивалентность и даже транспозиционную эквивалентность . Инверсионная эквивалентность мало используется в теории тонов , хотя предполагается, что множества, которые можно инвертировать друг в друга, имеют отдаленное общее. Однако в теории музыкальных множеств они считаются идентичными или почти идентичными.

Множества называются инверсионно-симметричными, если они отображаются сами на себя при инверсии. Шаг, вокруг которого должны быть инвертированы множества, называется осью симметрии (или центром). Ось может находиться либо на определенной высоте, либо на полпути между двумя высотами (при условии, что микротона не используются). Например, набор C–E ♭ –E–F ♯ –G–B ♭ имеет ось в F и ось, расположенную на расстоянии тритона, в B, если набор указан как F ♯ –G–B ♭ –C. –Э ♭ –Э. Другой пример: набор C–E–F–F ♯ –G–B имеет ось в диаде F/F ♯ и ось в B/C, если он указан как F ♯ –G–B–C–E. –Ф. ^[14]

Теория джаза

${ #(set-global-staff-size 15)\set Score.tempoHideNote = ##t \tempo 4 = 120\key c \major \time 4/4 \set Score.proportionalNotationDuration = #(ly:make-moment 1/2)\относительный с' { \ключ скрипичный \once \override NoteHead.color = #red c4^\markup { Melody } \once \override NoteHead.color = #red c g' g \once \override NoteHead.color = #red a \once \override NoteHead.color = # красный a g2 f4 подан c2 \bar "||"} }$

${ #(set-global-staff-size 15)\set Score.tempoHideNote = ##t \tempo 4 = 120\key c \major \time 4/4 \set Score.proportionalNotationDuration = #(ly:make-moment 1/2)\относительный с' { \ключ бас \once \override NoteHead.color = #red c4^\markup { Диатоническая инверсия относительно оси тангажа C } \once \override NoteHead.color = #red cf, Fee f2 g4 gaabb c2 \bar "||"} }$

${ #(set-global-staff-size 15)\set Score.tempoHideNote = ##t \tempo 4 = 120\key c \major \time 4/4 \set Score.proportionalNotationDuration = #(ly:make-moment 1/2)\относительный с' { \ключ бас \once \override NoteHead.color = #red c4^\markup { Хроматическая инверсия относительно оси основного тона C } \once \override NoteHead.color = #red cf, f es es f2 g4 g aes aes bes bes c2 \bar "|| "} }$

${ #(set-global-staff-size 15)\set Score.tempoHideNote = ##t \tempo 4 = 120\key c \major \time 4/4 \set Score.proportionalNotationDuration = #(ly:make-moment 1/2)\ относительно с'' { \ключ скрипичный fis4^\markup { Хроматическая инверсия относительно оси шага A } fis b, b \once \override NoteHead.color = #red a \once \override NoteHead.color = #red a b2 cis4 cis ddee fis2 \bar "||"} }$

${ #(set-global-staff-size 15)\set Score.tempoHideNote = ##t \tempo 4 = 120\key c \major \time 4/4 \set Score.proportionalNotationDuration = #(ly:make-moment 1/2)\ относительно с'' { \ключ скрипичный f4^\markup { Диатоническая инверсия относительно оси основного тона A } fb, b \once \override NoteHead.color = #red a \once \override NoteHead.color = #red a b2 c4 cddee f2 \bar "||"} }$

Инверсия оси тангажа песни " Twinkle, Twinkle, Little Star " относительно C и A.

В теории джаза ось высоты звука — это центр, вокруг которого инвертируется мелодия. ^[15]

«Ось тангажа» работает в контексте составной операции транспозиционной инверсии, где транспонирование выполняется после инверсии. Однако, в отличие от теории множеств, транспозиция может быть хроматической или диатонической транспозицией. Таким образом, если DAG (P5 вверх, M2 вниз) инвертируется в DGA (P5 вниз, M2 вверх), «ось тангажа» равна D. Однако, если она инвертируется в CFG, ось тангажа равна G, а если ось тангажа равна A , мелодия изменится на EAB.

Обозначение положения октавы может определять, сколько строк и пробелов разделяют одну ось. Ось тона DAG и его инверсии ADE либо находится между C/B ♮, либо между одинарной высотой тона F.

См. также

Примечания

^ Триада корневых позиций в конце не имеет пятой части над корнем. Это обычное явление при каденции из-за голосового ведения .

Ссылки

^ Шуйер (2008), с. 66. ^{[ неполная короткая цитата ]}
^ «Инверсия | Джаз, импровизация и гармония | Британника» . www.britanica.com . Проверено 26 января 2024 г.
^ Адаптировано из тактов 14–16, Парри Х (1897) «Растингтон». В: Сборник австралийских гимнов: издание гармонии , 1977, стр. 492. Кристофер Вордсворт «Смотрите, победитель торжествует».
^ Вятт, Кейт; Шредер, Карл (1998). Гармония и теория: всеобъемлющий источник для всех музыкантов . Корпорация Хэла Леонарда . п. 74. ИСБН 978-0-7935-7991-4 .
^ Таблица аккордов F/G - Хордсология
^ Лавлок, Уильям (1981), Основы музыки , Лондон: Bell & Hyman, стр. ^{[ нужна страница ]}, ISBN 0-7135-0744-6 .
^ Кристенсен, Томас. 1994. Рамо и музыкальная мысль в эпоху Просвещения, стр. 51–61. Кембридж
^ Скоулз, Перси А. (1954). История музыки слушателя . Том. 1 (7-е изд.). Лондон: Издательство Оксфордского университета. п. 95.
^ «Ривольджименто (итал.)». Гроув Музыка онлайн . 2001. doi : 10.1093/gmo/9781561592630.article.23544 . Обращение частей в двухчастном Обратном контрапункте.
^ Сервис, Том . (2014) «Симфонический гид: 41-я песня Моцарта ( Юпитер )», The Guardian , 27 мая.
^ Рэндел, Дон Майкл , изд. (2003). Гарвардский музыкальный словарь (четвертое изд.). Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. стр. 418 . ISBN 0674011635 . OCLC 52623743 .
^ Штраус, Джозеф Н. (1990). Введение в посттональную теорию . Энглвуд Клиффс, Нью-Джерси: Прентис Холл. стр. 34–35. ISBN 0136866921 . OCLC 20012239 .
^ Штраус 1990 , с. 36.
^ Уилсон, Пол (1992), Музыка Белы Бартока , издательство Йельского университета, стр. 10–11, ISBN 0-300-05111-5
^ Пиз, Тед (2003). Джазовая композиция: теория и практика , стр.152. ISBN 0-87639-001-7 .

Внешние ссылки

Обращения аккордов и упражнения для джазовой гитары

[4] Триада корневых позиций в конце не имеет пятой части над корнем. Это обычное явление при каденции из-за голосового ведения .

[1] Шуйер (2008), с. 66. ^{[ неполная короткая цитата ]}

[2] «Инверсия | Джаз, импровизация и гармония | Британника» . www.britanica.com . Проверено 26 января 2024 г.

[3] Адаптировано из тактов 14–16, Парри Х (1897) «Растингтон». В: Сборник австралийских гимнов: издание гармонии , 1977, стр. 492. Кристофер Вордсворт «Смотрите, победитель торжествует».

[5] Вятт, Кейт; Шредер, Карл (1998). Гармония и теория: всеобъемлющий источник для всех музыкантов . Корпорация Хэла Леонарда . п. 74. ИСБН 978-0-7935-7991-4 .

[6] Таблица аккордов F/G - Хордсология

[7] Лавлок, Уильям (1981), Основы музыки , Лондон: Bell & Hyman, стр. ^{[ нужна страница ]}, ISBN 0-7135-0744-6 .

[8] Кристенсен, Томас. 1994. Рамо и музыкальная мысль в эпоху Просвещения, стр. 51–61. Кембридж

[9] Скоулз, Перси А. (1954). История музыки слушателя . Том. 1 (7-е изд.). Лондон: Издательство Оксфордского университета. п. 95.

[10] «Ривольджименто (итал.)». Гроув Музыка онлайн . 2001. doi : 10.1093/gmo/9781561592630.article.23544 . Обращение частей в двухчастном Обратном контрапункте.

[11] Сервис, Том . (2014) «Симфонический гид: 41-я песня Моцарта ( Юпитер )», The Guardian , 27 мая.

[12] Рэндел, Дон Майкл , изд. (2003). Гарвардский музыкальный словарь (четвертое изд.). Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. стр. 418 . ISBN 0674011635 . OCLC 52623743 .

[13] Штраус, Джозеф Н. (1990). Введение в посттональную теорию . Энглвуд Клиффс, Нью-Джерси: Прентис Холл. стр. 34–35. ISBN 0136866921 . OCLC 20012239 .

[FOOTNOTEStraus199036-14] Штраус 1990 , с. 36.

[15] Уилсон, Пол (1992), Музыка Белы Бартока , издательство Йельского университета, стр. 10–11, ISBN 0-300-05111-5

[16] Пиз, Тед (2003). Джазовая композиция: теория и практика , стр.152. ISBN 0-87639-001-7 .

[1]

[2]

[3]

[а]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

v т и Двенадцатитоновая техника и сериализм
Fundamentals	Combinatoriality Complementation Derivation Hexachord Interval class Invariance Partition Cross partition Tone row Aggregate List
Permutations	Prime row Retrograde Inversion Retrograde inversion Multiplication
Notable composers	Milton Babbitt Pierre Boulez Josef Matthias Hauer Second Viennese School Alban Berg Arnold Schoenberg Anton Webern Charles Wuorinen ...more...
Related articles	All-interval twelve-tone row All-trichord hexachord Atonality Chromatic scale Duration series Equivalence Formula composition Modernism (music) Punctualism Semitone Set theory Time point Trope
List of dodecaphonic and serial compositions