Квантование (обработка сигналов)

Самый простой способ квантования сигнала — выбрать значение цифровой амплитуды, наиболее близкое к исходной аналоговой амплитуде. В этом примере показаны исходный аналоговый сигнал (зеленый), квантованный сигнал (черные точки), сигнал, восстановленный из квантованного сигнала (желтый) и разница между исходным сигналом и восстановленным сигналом (красный). Разница между исходным сигналом и восстановленным сигналом представляет собой ошибку квантования и в этой простой схеме квантования является детерминированной функцией входного сигнала.

Квантование в математике и цифровой обработке сигналов — это процесс преобразования входных значений из большого набора (часто непрерывного набора) в выходные значения в (счетном) меньшем наборе, часто с конечным числом элементов . Округление и усечение являются типичными примерами процессов квантования. Квантование в той или иной степени участвует практически во всех процессах цифровой обработки сигналов, поскольку процесс представления сигнала в цифровой форме обычно включает округление. Квантование также составляет основу практически всех алгоритмов сжатия с потерями .

Разница между входным значением и его квантованным значением (например, ошибкой округления ) называется ошибкой квантования . Устройство или алгоритмическая функция , выполняющая квантование, называется квантователем . Аналого -цифровой преобразователь является примером квантователя.

Пример

Например, округление действительного числа $x$ до ближайшего целого значения образует очень простой тип квантователя – унифицированный . Типичный ( средний шаг ) равномерный квантователь с размером шага квантования, равным некоторому значению. $\Delta$ может быть выражено как

$Q(x)=\Delta \cdot \left\lfloor {\frac {x}{\Delta }}+{\frac {1}{2}}\right\rfloor$,

где обозначение $\lfloor \ \rfloor$ обозначает функцию пола .

В качестве альтернативы тот же квантователь может быть выражен через функцию потолка , как

$Q(x)=\Delta \cdot \left\lceil {\frac {x}{\Delta }}-{\frac {1}{2}}\right\rceil$.

(Обозначение $\lceil \ \rceil$ обозначает функцию потолка).

Существенным свойством квантователя является наличие счетного набора возможных членов выходных значений, меньшего, чем набор возможных входных значений. Члены набора выходных значений могут иметь целые, рациональные или действительные значения. Для простого округления до ближайшего целого числа размер шага $\Delta$ равен 1. При $\Delta =1$ или с $\Delta$ равный любому другому целочисленному значению, этот квантователь имеет вещественные входы и целочисленные выходы.

Когда размер шага квантования (Δ) мал по сравнению с изменением квантованного сигнала, относительно просто показать, что среднеквадратическая ошибка, возникающая в результате такой операции округления, будет примерно равна $\Delta ^{2}/12$. Среднеквадратическую ошибку также называют мощностью шума квантования . Добавление одного бита к квантователю уменьшает вдвое значение Δ, что снижает мощность шума в раз. ⁠ 1/4 ​ ⁠ ​ . В децибелах изменение мощности шума равно $\scriptstyle 10\cdot \log _{10}(1/4)\ \approx \ -6\ \mathrm {dB} .$

Поскольку набор возможных выходных значений квантователя счетен, любой квантователь можно разложить на два отдельных этапа, которые можно назвать этапом классификации (или этапом прямого квантования ) и этапом реконструкции (или этапом обратного квантования ), где этап классификации отображает входное значение в целочисленный индекс квантования $k$ и этап реконструкции отображает индекс $k$ к стоимости реконструкции $y_{k}$ это выходное приближение входного значения. Для примера однородного квантователя, описанного выше, этап прямого квантования может быть выражен как

$k=\left\lfloor {\frac {x}{\Delta }}+{\frac {1}{2}}\right\rfloor$,

и этап реконструкции для этого примера квантователя просто

$y_{k}=k\cdot \Delta$.

Такое разложение полезно для проектирования и анализа поведения квантования и иллюстрирует, как квантованные данные могут передаваться по каналу связи : исходный кодер может выполнять этап прямого квантования и отправлять индексную информацию по каналу связи, а декодер — может выполнить этап реконструкции для получения выходной аппроксимации исходных входных данных. В общем, этап прямого квантования может использовать любую функцию, которая отображает входные данные в целочисленное пространство данных индекса квантования, а этап обратного квантования может концептуально (или буквально) представлять собой операцию поиска в таблице для сопоставления каждого индекса квантования с соответствующее значение реконструкции. Это двухэтапное разложение одинаково хорошо применимо как к векторным, так и к скалярным квантователям.

Математические свойства

Поскольку квантование представляет собой отображение «многие к немногим», это по своей сути нелинейный и необратимый процесс (т. е., поскольку одно и то же выходное значение используется несколькими входными значениями, в общем случае невозможно восстановить точное входное значение, когда задано только выходное значение).

Набор возможных входных значений может быть бесконечно большим и, возможно, непрерывным и, следовательно, неисчислимым (например, набор всех действительных чисел или всех действительных чисел в некотором ограниченном диапазоне). Набор возможных выходных значений может быть конечным или счетным . Входные и выходные наборы, участвующие в квантовании, можно определить довольно общим способом. Например, векторное квантование — это применение квантования к многомерным (векторным) входным данным.

Типы

2-битное разрешение с четырьмя уровнями квантования по сравнению с аналогом.

3-битное разрешение с восемью уровнями.

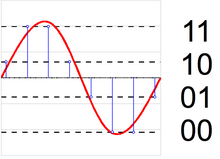
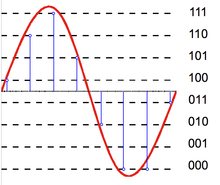
Аналого-цифровой преобразователь

Аналого -цифровой преобразователь (АЦП) можно смоделировать как два процесса: выборку и квантование. Выборка преобразует изменяющийся во времени сигнал напряжения в сигнал дискретного времени , представляющий собой последовательность действительных чисел. Квантование заменяет каждое действительное число приближением из конечного набора дискретных значений. Чаще всего эти дискретные значения представляются в виде слов с фиксированной точкой. Хотя возможно любое количество уровней квантования, обычная длина слова составляет 8 бит (256 уровней), 16 бит (65 536 уровней) и 24 бита (16,8 миллиона уровней). Квантование последовательности чисел приводит к последовательности ошибок квантования, которую иногда моделируют как аддитивный случайный сигнал, называемый шумом квантования, из-за его стохастического поведения. Чем больше уровней использует квантователь, тем ниже мощность его шума квантования.

Оптимизация скорости и искажений

Квантование , оптимизированное по скорости искажения, встречается при исходном кодировании для алгоритмов сжатия данных с потерями, целью которых является управление искажениями в пределах скорости передачи данных , поддерживаемой каналом связи или носителем данных. Анализ квантования в этом контексте включает изучение объема данных (обычно измеряемого в цифрах, битах или скорости передачи данных ), который используется для представления выходного сигнала квантователя, и изучение потери точности, вносимой процессом квантования (который называется искажением ) .

Равномерные квантователи со средним подступенком и средним протектором

Большинство унифицированных квантователей для входных данных со знаком можно отнести к одному из двух типов: промежуточный и промежуточный . Терминология основана на том, что происходит в области вокруг значения 0, и использует аналогию рассмотрения функции ввода-вывода квантователя как лестницы . Квантизаторы средней ступени имеют нулевой уровень реконструкции (соответствует ступени лестницы), тогда как квантователи средней ступени имеют порог классификации с нулевым значением (соответствует подступенку лестницы ).

Квантование в середине протектора включает округление. Формулы для равномерного квантования в середине протектора представлены в предыдущем разделе.

$Q(x)=\Delta \cdot \left\lfloor {\frac {x}{\Delta }}+{\frac {1}{2}}\right\rfloor$,

Квантование среднего уровня включает усечение. Формула ввода-вывода для равномерного квантователя среднего уровня определяется следующим образом:

$Q(x)=\Delta \cdot \left(\left\lfloor {\frac {x}{\Delta }}\right\rfloor +{\frac {1}{2}}\right)$,

где правило классификации определяется выражением

$k=\left\lfloor {\frac {x}{\Delta }}\right\rfloor$

и правило реконструкции

$y_{k}=\Delta \cdot \left(k+{\tfrac {1}{2}}\right)$.

Обратите внимание, что однородные квантователи со средней высотой не имеют нулевого выходного значения — их минимальная выходная величина составляет половину размера шага. Напротив, квантователи средней ступени имеют нулевой уровень выходного сигнала. Для некоторых приложений может оказаться необходимым наличие нулевого представления выходного сигнала.

В общем, квантователь со средним подступенком или средней ступенью на самом деле может не быть однородным квантователя квантователем, т. е. не все размеры классификационных интервалов могут быть одинаковыми или расстояние между его возможными выходными значениями может не быть одинаковым. . Отличительной характеристикой квантователя средней ступени является то, что он имеет пороговое значение классификации, которое равно нулю, а отличительной характеристикой квантователя средней ступени является то, что он имеет значение восстановления, которое точно равно нулю.

Квантизаторы мертвой зоны

Квантизатор мертвой зоны — это тип квантователя в середине шага с симметричным поведением вокруг 0. Область вокруг нулевого выходного значения такого квантователя называется мертвой зоной или зоной нечувствительности . Мертвая зона иногда может служить той же цели, что и шумоподавитель или функция шумоподавления . Специально для приложений сжатия мертвая зона может иметь другую ширину, чем ширина для других ступеней. Для однородного в остальном квантователя ширина мертвой зоны может быть установлена ​​на любое значение. $w$ используя правило прямого квантования

$k=\operatorname {sgn}(x)\cdot \max \left(0,\left\lfloor {\frac {\left|x\right|-w/2}{\Delta }}+1\right\rfloor \right)$,

где функция $\operatorname {sgn}$( ) — знаковая функция (также известная как функция Signum ). Общее правило восстановления для такого квантователя мертвой зоны определяется выражением

$y_{k}=\operatorname {sgn}(k)\cdot \left({\frac {w}{2}}+\Delta \cdot (|k|-1+r_{k})\right)$,

где $r_{k}$ — значение смещения реконструкции в диапазоне от 0 до 1 в виде доли размера шага. Обычно $0\leq r_{k}\leq {\tfrac {1}{2}}$ при квантовании входных данных с помощью типичной функции плотности вероятности (PDF), которая симметрична относительно нуля и достигает своего пикового значения в нуле (например, гауссиан , лапласиан или обобщенный гауссиан PDF). Хотя $r_{k}$ может зависеть от $k$ в общем случае и может быть выбран для выполнения условия оптимальности, описанного ниже, часто ему просто присваивается константа, например ${\tfrac {1}{2}}$. (Обратите внимание, что в этом определении $y_{0}=0$ из-за определения $\operatorname {sgn}$( ) функция, поэтому $r_{0}$ не имеет никакого эффекта.)

Очень часто используемый частный случай (например, схема, обычно используемая в финансовом учете и элементарной математике) состоит в том, чтобы установить $w=\Delta$ и $r_{k}={\tfrac {1}{2}}$ для всех $k$. В этом случае квантователь мертвой зоны также является однородным квантователем, поскольку центральная мертвая зона этого квантователя имеет ту же ширину, что и все его другие шаги, и все его значения восстановления также расположены на одинаковом расстоянии друг от друга.

Характеристики шума и ошибок

Модель аддитивного шума

Распространенным предположением при анализе ошибки квантования является то, что она влияет на систему обработки сигналов аналогично аддитивному белому шуму – имея незначительную корреляцию с сигналом и примерно плоскую спектральную плотность мощности . Модель аддитивного шума обычно используется для анализа эффектов ошибок квантования в системах цифровой фильтрации и может быть очень полезна в таком анализе. Было показано, что эта модель действительна в случаях квантования с высоким разрешением (небольшие размеры). $\Delta$ относительно уровня сигнала) с гладкими PDF-файлами.

Поведение аддитивного шума не всегда является верным предположением. Ошибка квантования (для квантователей, определенных, как описано здесь) детерминированно связана с сигналом и не полностью от него независима. Таким образом, периодические сигналы могут создавать периодический шум квантования. А в некоторых случаях это может даже привести к появлению предельных циклов в системах цифровой обработки сигналов. Одним из способов обеспечить эффективную независимость ошибки квантования от исходного сигнала является выполнение со сглаживанием квантования (иногда с формированием шума ), которое включает добавление случайного (или псевдослучайного ) шума к сигналу перед квантованием.

Модели ошибок квантования

В типичном случае исходный сигнал намного больше одного младшего бита (LSB). В этом случае ошибка квантования незначительно коррелирует с сигналом и имеет приблизительно равномерное распределение . Когда для квантования используется округление, ошибка квантования имеет среднее значение , равное нулю, а среднеквадратичное значение (RMS) представляет собой стандартное отклонение этого распределения, определяемое выражением $\scriptstyle {\frac {1}{\sqrt {12}}}\mathrm {LSB} \ \approx \ 0.289\,\mathrm {LSB}$. При использовании усечения ошибка имеет ненулевое среднее значение. $\scriptstyle {\frac {1}{2}}\mathrm {LSB}$ и среднеквадратичное значение $\scriptstyle {\frac {1}{\sqrt {3}}}\mathrm {LSB}$. Хотя округление дает меньшую среднеквадратическую ошибку, чем усечение, разница обусловлена ​​только статическим (DC) членом $\scriptstyle {\frac {1}{2}}\mathrm {LSB}$. Среднеквадратические значения ошибки по переменному току в обоих случаях одинаковы, поэтому нет особого преимущества округления перед усечением в ситуациях, когда член ошибки по постоянному току можно игнорировать (например, в системах, связанных по переменному току). В любом случае стандартное отклонение, выраженное в процентах от полного диапазона сигнала, изменяется в 2 раза при каждом изменении количества бит квантования на 1 бит. Таким образом, потенциальное отношение мощности сигнала к шуму квантования изменяется на 4, или $\scriptstyle 10\cdot \log _{10}(4)$, примерно 6 дБ на бит.

При более низких амплитудах ошибка квантования становится зависимой от входного сигнала, что приводит к искажениям. Это искажение создается после фильтра сглаживания, и если эти искажения превышают половину частоты дискретизации, они возвращаются в интересующую полосу. Чтобы сделать ошибку квантования независимой от входного сигнала, сигнал подвергается сглаживанию путем добавления к сигналу шума. Это немного снижает соотношение сигнал/шум, но позволяет полностью устранить искажения.

Модель шума квантования

Сравнение квантования синусоиды до 64 уровней (6 бит) и 256 уровней (8 бит). Аддитивный шум, создаваемый 6-битным квантованием, на 12 дБ больше, чем шум, создаваемый 8-битным квантованием. Когда спектральное распределение плоское, как в этом примере, разница в 12 дБ проявляется как измеримая разница в минимальном уровне шума.

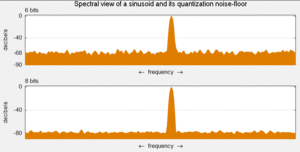
Шум квантования — это модель ошибки квантования, вносимой квантованием в АЦП. Это ошибка округления между аналоговым входным напряжением АЦП и выходным цифровым значением. Шум нелинейный и зависит от сигнала. Его можно смоделировать несколькими различными способами.

В идеальном АЦП, где ошибка квантования равномерно распределена между −1/2 LSB и +1/2 LSB, а сигнал имеет равномерное распределение, охватывающее все уровни квантования, отношение сигнал/шум квантования (SQNR) может рассчитываться из

$\mathrm {SQNR} =20\log _{10}(2^{Q})\approx 6.02\cdot Q\ \mathrm {dB} \,\!$

где Q — количество битов квантования.

Наиболее распространенными тестовыми сигналами, отвечающими этому требованию, являются треугольные волны полной амплитуды и пилообразные волны .

Например, 16-битный АЦП имеет максимальное отношение сигнал/шум квантования 6,02 × 16 = 96,3 дБ.

Когда входной сигнал представляет собой синусоидальную волну полной амплитуды , распределение сигнала больше не является равномерным, и вместо этого соответствующее уравнение имеет вид

$\mathrm {SQNR} \approx 1.761+6.02\cdot Q\ \mathrm {dB} \,\!$

Здесь снова предполагается , что шум квантования распределен равномерно. Это тот случай, когда входной сигнал имеет большую амплитуду и широкий частотный спектр. В этом случае 16-битный АЦП имеет максимальное отношение сигнал/шум 98,09 дБ. Разница в соотношении сигнал-шум в 1,761 возникает только из-за того, что сигнал представляет собой полномасштабную синусоидальную волну, а не треугольник или пилообразную форму.

Для сложных сигналов в АЦП высокого разрешения это точная модель. Для АЦП с низким разрешением, сигналов низкого уровня в АЦП с высоким разрешением и для простых сигналов шум квантования распределяется неравномерно, что делает эту модель неточной. В этих случаях на распределение шума квантования сильно влияет точная амплитуда сигнала.

Расчеты относятся к полномасштабным входным данным. Для сигналов меньшего размера относительное искажение квантования может быть очень большим. аналоговое компандирование Чтобы обойти эту проблему, можно использовать , но это может привести к искажениям.

Дизайн

Гранулярные искажения и искажения от перегрузки

Часто конструкция квантователя предполагает поддержку только ограниченного диапазона возможных выходных значений и выполнение ограничения для ограничения выходного сигнала этим диапазоном всякий раз, когда входной сигнал превышает поддерживаемый диапазон. Ошибка, вызванная этим ограничением, называется искажением перегрузки . В крайних пределах поддерживаемого диапазона величина интервала между выбираемыми выходными значениями квантователя называется его степенью детализации , а ошибка, вносимая этим интервалом, называется гранулярным искажением. Обычно при проектировании квантователя необходимо определить правильный баланс между гранулярными искажениями и искажениями из-за перегрузки. Для заданного поддерживаемого количества возможных выходных значений уменьшение среднего гранулярного искажения может привести к увеличению среднего искажения от перегрузки, и наоборот. Метод управления амплитудой сигнала (или, что то же самое, размером шага квантования). $\Delta$) для достижения соответствующего баланса используется автоматическая регулировка усиления (АРУ). Однако в некоторых конструкциях квантователей концепции гранулярной ошибки и ошибки перегрузки могут не применяться (например, для квантователя с ограниченным диапазоном входных данных или со счетным бесконечным набором выбираемых выходных значений).

Конструкция квантователя скорости-искажения

Скалярный квантователь, выполняющий операцию квантования, обычно можно разбить на два этапа:

Классификация

Процесс, который классифицирует диапазон входного сигнала на $M$ непересекающиеся интервалы $\{I_{k}\}_{k=1}^{M}$, определив $M-1$ решения граничные значения $\{b_{k}\}_{k=1}^{M-1}$, такой, что $I_{k}=[b_{k-1}~,~b_{k})$ для $k=1,2,\ldots ,M$, с крайними пределами, определяемыми $b_{0}=-\infty$ и $b_{M}=\infty$. Все входы $x$ которые попадают в заданный интервал интервала $I_{k}$ связаны с одним и тем же индексом квантования $k$.

Реконструкция

Каждый интервал $I_{k}$ представлено значением реконструкции $y_{k}$ который реализует отображение $x\in I_{k}\Rightarrow y=y_{k}$.

Эти два этапа вместе составляют математическую операцию $y=Q(x)$.

Методы энтропийного кодирования могут применяться для передачи индексов квантования от исходного кодера, который выполняет этап классификации, в декодер, который выполняет этап реконструкции. Один из способов сделать это — связать каждый индекс квантования $k$ с двоичным кодовым словом $c_{k}$. Важным фактором является количество битов, используемых для каждого кодового слова, обозначенное здесь как $\mathrm {length} (c_{k})$. В результате конструкция $M$Квантизатор двухуровневого уровня и связанный с ним набор кодовых слов для передачи значений его индекса требуют нахождения значений $\{b_{k}\}_{k=1}^{M-1}$, $\{c_{k}\}_{k=1}^{M}$ и $\{y_{k}\}_{k=1}^{M}$ которые оптимально удовлетворяют выбранному набору конструктивных ограничений, таких как скорость передачи данных $R$ и искажение $D$.

Предполагая, что источник информации $S$ производит случайные величины $X$ со связанным PDF-файлом $f(x)$, вероятность $p_{k}$ что случайная величина попадает в определенный интервал квантования $I_{k}$ дается:

$p_{k}=P[x\in I_{k}]=\int _{b_{k-1}}^{b_{k}}f(x)dx$.

Результирующая скорость передачи данных $R$, в единицах среднего количества битов на квантованное значение, для этого квантователя можно получить следующим образом:

$R=\sum _{k=1}^{M}p_{k}\cdot \mathrm {length} (c_{k})=\sum _{k=1}^{M}\mathrm {length} (c_{k})\int _{b_{k-1}}^{b_{k}}f(x)dx$.

Если предположить, что искажение измеряется среднеквадратичной ошибкой, искажение D определяется выражением:

$D=E[(x-Q(x))^{2}]=\int _{-\infty }^{\infty }(x-Q(x))^{2}f(x)dx=\sum _{k=1}^{M}\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx$.

Ключевое наблюдение заключается в том, что скорость $R$ зависит от границ решения $\{b_{k}\}_{k=1}^{M-1}$ и длины кодовых слов $\{\mathrm {length} (c_{k})\}_{k=1}^{M}$, тогда как искажение $D$ зависит от границ решения $\{b_{k}\}_{k=1}^{M-1}$ и уровни реконструкции $\{y_{k}\}_{k=1}^{M}$.

После определения этих двух показателей производительности для квантователя типичная формулировка коэффициента искажений для задачи проектирования квантователя может быть выражена одним из двух способов:

1. Учитывая максимальное ограничение искажений $D\leq D_{\max }$, минимизировать битрейт $R$
2. Учитывая ограничение максимальной скорости передачи данных $R\leq R_{\max }$, минимизировать искажения $D$

Часто решение этих проблем может быть эквивалентно (или приближенно) выражено и решено путем преобразования формулировки к задаче без ограничений. $\min \left\{D+\lambda \cdot R\right\}$ где множитель Лагранжа $\lambda$ — неотрицательная константа, устанавливающая соответствующий баланс между скоростью и искажениями. Решение задачи без ограничений эквивалентно поиску точки на выпуклой оболочке семейства решений эквивалентной постановки задачи с ограничениями. Однако найти решение – особенно решение в закрытой форме – для любой из этих трех формулировок проблемы может быть сложно. Решения, не требующие методов многомерной итеративной оптимизации, были опубликованы только для трех PDF-файлов: унифицированного, экспоненциальный , и лапласиан распределения. Итерационные подходы к оптимизации можно использовать для поиска решений и в других случаях.

Обратите внимание, что значения реконструкции $\{y_{k}\}_{k=1}^{M}$ влияют только на искажения – они не влияют на скорость передачи данных – и что каждый отдельный $y_{k}$ вносит отдельный вклад $d_{k}$ к общему искажению, как показано ниже:

$D=\sum _{k=1}^{M}d_{k}$

где

$d_{k}=\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx$

Это наблюдение можно использовать для облегчения анализа – учитывая набор $\{b_{k}\}_{k=1}^{M-1}$ ценности, ценность каждого $y_{k}$ может быть оптимизирован отдельно, чтобы минимизировать вклад в искажения $D$.

Для критерия искажения среднеквадратической ошибки можно легко показать, что оптимальный набор значений реконструкции $\{y_{k}^{*}\}_{k=1}^{M}$ задается путем установки значения реконструкции $y_{k}$ внутри каждого интервала $I_{k}$ к условному ожидаемому значению (также называемому центроидом ) в пределах интервала, определяемому формулой:

$y_{k}^{*}={\frac {1}{p_{k}}}\int _{b_{k-1}}^{b_{k}}xf(x)dx$.

Использование достаточно хорошо разработанных методов энтропийного кодирования может привести к использованию скорости передачи данных, близкой к истинному информационному содержанию индексов. $\{k\}_{k=1}^{M}$, такой, что эффективно

$\mathrm {length} (c_{k})\approx -\log _{2}\left(p_{k}\right)$

и поэтому

$R=\sum _{k=1}^{M}-p_{k}\cdot \log _{2}\left(p_{k}\right)$.

Использование этого приближения может позволить отделить проблему проектирования энтропийного кодирования от проектирования самого квантователя. Современные методы энтропийного кодирования, такие как арифметическое кодирование, могут обеспечить скорость передачи данных, очень близкую к истинной энтропии источника, с учетом набора известных (или адаптивно оцененных) вероятностей. $\{p_{k}\}_{k=1}^{M}$.

В некоторых проектах вместо оптимизации для определенного количества областей классификации $M$, проблема проектирования квантователя может включать оптимизацию значения $M$ также. Для некоторых вероятностных моделей источников наилучшая производительность может быть достигнута, когда $M$ приближается к бесконечности.

Пренебрежение ограничением энтропии: квантование Ллойда – Макса.

В приведенной выше формулировке, если ограничением скорости передачи данных пренебречь, установив $\lambda$ равное 0, или, что то же самое, если предполагается, что для представления квантованных данных будет использоваться код фиксированной длины (FLC) вместо кода переменной длины (или какой-либо другой технологии энтропийного кодирования, такой как арифметическое кодирование, которая лучше, чем FLC в смысле скорости–искажений), задача оптимизации сводится к минимизации искажений $D$ один.

Индексы, производимые $M$Квантизатор двухуровневого уровня может быть закодирован с использованием кода фиксированной длины, используя $R=\lceil \log _{2}M\rceil$ биты/символ. Например, когда $M=$256 уровней, битрейт FLC $R$ составляет 8 бит/символ. По этой причине такой квантователь иногда называют 8-битным квантователем. Однако использование FLC исключает улучшение сжатия, которое можно получить за счет использования лучшего энтропийного кодирования.

Предполагая FLC с $M$ На разных уровнях проблема минимизации скорости-искажения может быть сведена только к минимизации искажений. Сведенную задачу можно сформулировать следующим образом: задан источник $X$ с PDF $f(x)$ и ограничение, согласно которому квантователь должен использовать только $M$ классификация регионов, найти границы решения $\{b_{k}\}_{k=1}^{M-1}$ и уровни реконструкции $\{y_{k}\}_{k=1}^{M}$ чтобы минимизировать возникающие искажения

$D=E[(x-Q(x))^{2}]=\int _{-\infty }^{\infty }(x-Q(x))^{2}f(x)dx=\sum _{k=1}^{M}\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx=\sum _{k=1}^{M}d_{k}$.

Поиск оптимального решения вышеуказанной проблемы приводит к появлению квантователя, который иногда называют решением MMSQE (минимальная среднеквадратическая ошибка квантования), а полученный в результате квантователь, оптимизированный для PDF (неравномерный), называется квантователем Ллойда – Макса , названным в честь два человека, которые независимо друг от друга разработали итеративные методы решить две системы одновременных уравнений, возникающих в результате ${\partial D/\partial b_{k}}=0$ и ${\partial D/\partial y_{k}}=0$, следующее:

${\partial D \over \partial b_{k}}=0\Rightarrow b_{k}={y_{k}+y_{k+1} \over 2}$,

который помещает каждый порог в среднюю точку между каждой парой значений реконструкции, и

${\partial D \over \partial y_{k}}=0\Rightarrow y_{k}={\int _{b_{k-1}}^{b_{k}}xf(x)dx \over \int _{b_{k-1}}^{b_{k}}f(x)dx}={\frac {1}{p_{k}}}\int _{b_{k-1}}^{b_{k}}xf(x)dx$

который помещает каждое значение реконструкции в центроид (условное ожидаемое значение) соответствующего классификационного интервала.

Алгоритм Ллойда I , первоначально описанный в 1957 году, можно легко обобщить для применения к векторным данным. Результатом этого обобщения являются методы оптимизации классификатора Линде – Бьюзо – Грея (LBG) или k-средних . Более того, этот метод можно дополнительно обобщить, включив в него также ограничение энтропии для векторных данных.

Равномерное квантование и приближение 6 дБ/бит

Квантизатор Ллойда-Макса на самом деле является равномерным квантователем, когда входной PDF равномерно распределен по диапазону $[y_{1}-\Delta /2,~y_{M}+\Delta /2)$. Однако для источника, который не имеет равномерного распределения, квантователь с минимальными искажениями может не быть равномерным квантователем. Анализ однородного квантователя, примененного к равномерно распределенному источнику, можно резюмировать следующим образом:

Симметричный источник X можно смоделировать с помощью $f(x)={\tfrac {1}{2X_{\max }}}$, для $x\in [-X_{\max },X_{\max }]$ и 0 в другом месте.Размер шага $\Delta ={\tfrac {2X_{\max }}{M}}$ а отношение сигнал/шум квантования (SQNR) квантователя равно

${\rm {SQNR}}=10\log _{10}{\frac {\sigma _{x}^{2}}{\sigma _{q}^{2}}}=10\log _{10}{\frac {(M\Delta )^{2}/12}{\Delta ^{2}/12}}=10\log _{10}M^{2}=20\log _{10}M$.

Для кода фиксированной длины, используя $N$ биты, $M=2^{N}$, в результате чего ${\rm {SQNR}}=20\log _{10}{2^{N}}=N\cdot (20\log _{10}2)=N\cdot 6.0206\,{\rm {dB}}$,

или приблизительно 6 дБ на бит. Например, для $N$=8 бит, $M$=256 уровней и SQNR = 8×6 = 48 дБ; и для $N$= 16 бит, $M$=65536 и SQNR = 16×6 = 96 дБ. Свойство улучшения SQNR на 6 дБ для каждого дополнительного бита, используемого при квантовании, является хорошо известным показателем качества. Однако его следует использовать с осторожностью: этот вывод применим только для однородного квантователя, примененного к однородному источнику. Для других исходных PDF-файлов и других конструкций квантователей SQNR может несколько отличаться от прогнозируемого на 6 дБ/бит, в зависимости от типа PDF-файла, типа источника, типа квантователя и диапазона скорости передачи данных.

Однако принято предполагать, что для многих источников крутизна функции квантования SQNR может быть приблизительно равна 6 дБ/бит при работе на достаточно высокой скорости передачи данных. При асимптотически высоких скоростях передачи данных сокращение размера шага вдвое увеличивает скорость передачи данных примерно на 1 бит на выборку (поскольку 1 бит необходим для указания того, находится ли значение в левой или правой половине предыдущего интервала двойного размера) и уменьшает среднеквадратическую ошибку в 4 раза (т. е. 6 дБ) на основе $\Delta ^{2}/12$ приближение.

При асимптотически высоких скоростях передачи данных приближение 6 дБ/бит подтверждается для многих исходных PDF-файлов строгим теоретическим анализом. Более того, структура оптимального скалярного квантователя (в смысле скорости-искажения) в этих условиях приближается к структуре однородного квантователя.

В других областях

См. Также: Квантовый шум и квантовый предел.

Многие физические величины фактически квантуются физическими объектами. Примеры областей, в которых применяется это ограничение, включают электронику (из-за электронов ), оптику (из-за фотонов ), биологию (из-за ДНК ), физику (из-за пределов Планка ) и химию (из-за молекул ).

См. также

• Бета-кодер
• Квантование цвета
• Объединение данных
• Дискретизация
• Ошибка дискретизации
• Постеризация
• Импульсно-кодовая модуляция
• Квантиль
• Квантование (обработка изображений)
• Разбавление регрессии - смещение в оценках параметров, вызванное такими ошибками, как квантование объясняющей или независимой переменной.

Ссылки

• Саюд, Халид (2005), Введение в сжатие данных, третье издание , Морган Кауфманн, ISBN  978-0-12-620862-7
• Джаянт, Никил С.; Нолл, Питер (1984), Цифровое кодирование сигналов: принципы и приложения к речи и видео , Прентис-Холл, ISBN  978-0-13-211913-9
• Грегг, В. Дэвид (1977), Аналоговая и цифровая связь , Джон Уайли, ISBN  978-0-471-32661-8
• Штейн, Сеймур; Джонс, Дж. Джей (1967), Современные принципы коммуникации , МакГроу – Хилл , ISBN  978-0-07-061003-3

Дальнейшее чтение

• Бернард Уидроу; Иштван Коллар (2007). Шум квантования в цифровых вычислениях, обработке сигналов и управлении . Издательство Кембриджского университета. ISBN  9780521886710 .

См. также

• Наименьшее количество