Закон Кулона

Величина электростатической силы F между двумя точечными зарядами q ₁ и q ₂ прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Аналогичные заряды отталкиваются, а противоположные заряды притягиваются.

Закон обратных квадратов Кулона , или просто закон Кулона , является экспериментальным законом. физики , которая вычисляет величину силы между двумя электрически заряженными частицами в состоянии покоя. Эту электрическую силу условно называют электростатической силой или силой Кулона . Хотя закон был известен и раньше, впервые его опубликовал в 1785 году французский физик Шарль-Огюстен де Кулон . Закон Кулона сыграл важную роль в развитии теории электромагнетизма и, возможно, даже в ее отправной точке. поскольку это позволило осмысленно обсуждать количество электрического заряда в частице.

Закон гласит, что величина или абсолютная величина электростатической силы притяжения или отталкивания между двумя точечными зарядами прямо пропорциональна произведению величин их зарядов и обратно пропорциональна квадрату расстояния между ними. Кулон обнаружил, что тела с одинаковыми электрическими зарядами отталкиваются:

Таким образом, из этих трех испытаний следует, что сила отталкивания, которую два шара, [которые были] наэлектризованы одинаковым видом электричества, оказывают друг на друга, обратно пропорциональна квадрату расстояния.

Кулон также показал, что противоположно заряженные тела притягиваются по закону обратных квадратов: $$|F|=k_{\text{e}}{\frac {|q_{1}||q_{2}|}{r^{2}}}$$

Здесь k _e — константа, q ₁ и q ₂ — величины каждого заряда, а скаляр r — расстояние между зарядами.

Сила действует вдоль прямой линии, соединяющей два заряда. Если заряды имеют одинаковый знак, электростатическая сила между ними заставляет их отталкиваться; если у них разные знаки, сила между ними заставляет их притягиваться.

Будучи законом обратных квадратов , этот закон аналогичен Исаака Ньютона закону обратных квадратов всемирного тяготения , но гравитационные силы всегда заставляют предметы притягиваться, а электростатические силы заставляют заряды притягиваться или отталкиваться. Кроме того, гравитационные силы намного слабее электростатических сил. Закон Кулона можно использовать для вывода закона Гаусса и наоборот. В случае покоящегося точечного заряда эти два закона эквивалентны и выражают один и тот же физический закон по-разному. Закон был тщательно проверен , и наблюдения подтвердили закон по шкале от 10. ⁻¹⁶ м до 10 ⁸ м.

История

Шарль Огюстен де Кулон

Древние культуры Средиземноморья знали , что некоторые предметы, такие как янтарные палочки , можно натереть кошачьей шерстью, чтобы притянуть к себе легкие предметы, такие как перья и кусочки бумаги. Фалес Милетский сделал первое письменное описание статического электричества около 600 г. до н. э. когда он заметил, что трение может заставить кусок янтаря притягивать мелкие предметы.

В 1600 году английский учёный Уильям Гилберт тщательно изучил электричество и магнетизм, отличив эффект магнита от статического электричества, возникающего при трении янтаря. Он придумал неолатинское слово electricus («янтарный» или «подобный янтарю», от ἤλεκτρον [ электрон ], греческого слова «янтарь») для обозначения свойства притягивать мелкие предметы после трения. Эта ассоциация породила английские слова «электрический» и «электричество», которые впервые появились в печати в Томаса Брауна в «Эпидемической эпидемии» 1646 году.

Среди первых исследователей XVIII века, которые подозревали, что электрическая сила уменьшается с расстоянием так же, как и сила гравитации (т. е. как обратный квадрат расстояния), был Даниэль Бернулли. и Алессандро Вольта , оба измерившие силу между пластинами конденсатора , и Франц Эпин, который предположил закон обратных квадратов в 1758 году.

Основываясь на экспериментах с электрически заряженными сферами, Джозеф Пристли из Англии был одним из первых, кто предположил, что электрическая сила подчиняется закону обратных квадратов , подобному закону всемирного тяготения Ньютона . Однако он не обобщал и не уточнял это. В 1767 году он предположил, что сила между зарядами изменяется обратно пропорционально квадрату расстояния.

Кулона Торсионные весы

В 1769 году шотландский физик Джон Робисон объявил, что, согласно его измерениям, сила отталкивания между двумя сферами с зарядами одного знака изменяется как x ^−2.06 .

В начале 1770-х годов зависимость силы между заряженными телами от расстояния и заряда уже была открыта, но не опубликована Генри Кавендишем из Англии. В своих заметках Кавендиш писал: «Поэтому мы можем заключить, что электрическое притяжение и отталкивание должны быть обратно пропорциональны некоторой степени расстояния между расстояниями 2 + ⁠ 1/50 - ⁠ й й и 2- ⁠ 1/50 " . ⁠ th , и нет оснований думать, что оно вообще отличается от обратного коэффициента дублирования

Наконец, в 1785 году французский физик Шарль-Огюстен де Кулон опубликовал свои первые три отчета об электричестве и магнетизме, в которых сформулировал свой закон. Эта публикация имела важное значение для развития теории электромагнетизма . Он использовал крутильные весы для изучения сил отталкивания и притяжения заряженных частиц и определил, что величина электрической силы между двумя точечными зарядами прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними.

Торсионные весы состоят из стержня, подвешенного к его середине на тонком волокне. Волокно действует как очень слабая торсионная пружина . В эксперименте Кулона торсионные весы представляли собой изолирующий стержень с металлическим прикрепленным к одному концу шариком с покрытием, подвешенным на шелковой нити. Шар зарядили известным зарядом статического электричества , и к нему поднесли второй заряженный шар той же полярности. Два заряженных шарика отталкивались друг от друга, скручивая волокно под определенным углом, который можно было прочитать по шкале на приборе . Зная, какая сила потребуется, чтобы скрутить волокно на заданный угол, Кулон смог вычислить силу между шариками и вывести свой закон пропорциональности обратных квадратов.

Математическая форма

На изображении вектор F ₁ представляет собой силу, испытываемую q ₁ , а вектор F ₂ представляет собой силу, испытываемую q ₂ . При q ₁ q ₂ > 0 силы отталкивания (как на изображении), а при q ₁ q ₂ < 0 силы притяжения (напротив изображения). Величина сил всегда будет одинаковой.

Закон Кулона гласит, что электростатическая сила ${\textstyle \mathbf {F} _{1}}$ испытал заряд, $q_{1}$ на позиции $\mathbf {r} _{1}$, вблизи другого заряда, $q_{2}$ на позиции $\mathbf {r} _{2}$, в вакууме равна $$\mathbf {F} _{1}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{{\hat {\mathbf {r} }}_{12} \over {|\mathbf {r} _{12}|}^{2}}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{\mathbf {r} _{12} \over {|\mathbf {r} _{12}|}^{3}}$$

где ${\textstyle \mathbf {r_{12}=r_{1}-r_{2}} }$ – вектор смещения между зарядами, ${\textstyle {\hat {\mathbf {r} }}_{12}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{12}}{|\mathbf {r} _{12}|}}}$ единичный вектор, указывающий из ${\textstyle q_{2}}$ к ${\textstyle q_{1}}$, и $\varepsilon _{0}$ электрическая постоянная . Здесь, ${\textstyle \mathbf {\hat {r}} _{12}}$ используется для векторной записи. Электростатическая сила ${\textstyle \mathbf {F} _{2}}$ опытный $q_{2}$, согласно третьему закону Ньютона , ${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$.

Если оба заряда имеют одинаковый знак (как заряды), то произведение $q_{1}q_{2}$ положительно, а направление силы, действующей на $q_{1}$ дается ${\textstyle {\widehat {\mathbf {r} }}_{12}}$; заряды отталкиваются друг от друга. Если заряды имеют противоположные знаки, то произведение $q_{1}q_{2}$ отрицательно, а направление силы, действующей на $q_{1}$ является ${\textstyle -{\hat {\mathbf {r} }}_{12}}$; заряды притягиваются друг к другу.

Система дискретных зарядов

Закон суперпозиции позволяет распространить закон Кулона на любое количество точечных зарядов. Сила, действующая на точечный заряд со стороны системы точечных зарядов, представляет собой просто векторное сложение отдельных сил, действующих отдельно на этот точечный заряд со стороны каждого из зарядов. Результирующий вектор силы параллелен вектору электрического поля в этой точке, при этом точечный заряд удален.

Сила ${\textstyle \mathbf {F} }$ за небольшую плату $q$ на позиции $\mathbf {r}$, благодаря системе ${\textstyle n}$ дискретные заряды в вакууме

$$\mathbf {F} (\mathbf {r} )={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}}={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{\mathbf {r} _{i} \over {|\mathbf {r} _{i}|}^{3}},$$

где $q_{i}$ - величина i -го заряда, ${\textstyle \mathbf {r} _{i}}$ вектор от его положения до $\mathbf {r}$ и ${\textstyle {\hat {\mathbf {r} }}_{i}}$ — единичный вектор в направлении $\mathbf {r} _{i}$.

Непрерывное распределение заряда

принцип линейной суперпозиции В этом случае также используется . Для непрерывного распределения заряда интеграл по области, содержащей заряд, эквивалентен бесконечному суммированию, рассматривающему каждый бесконечно малый элемент пространства как точечный заряд. $dq$. Распределение заряда обычно линейное, поверхностное или объемное.

Для линейного распределения заряда (хорошее приближение заряда в проводе), где $\lambda (\mathbf {r} ')$ дает заряд на единицу длины в позиции $\mathbf {r} '$, и $d\ell '$ является бесконечно малым элементом длины, $$dq'=\lambda (\mathbf {r'} )\,d\ell '.$$

Для распределения поверхностного заряда (хорошее приближение заряда на пластине в конденсаторе с параллельными пластинами ), где $\sigma (\mathbf {r} ')$ дает заряд на единицу площади в позиции $\mathbf {r} '$, и $dA'$ бесконечно малый элемент площади, $$dq'=\sigma (\mathbf {r'} )\,dA'.$$

Для объемного распределения заряда (например, заряда в объеме металла), где $\rho (\mathbf {r} ')$ дает заряд на единицу объема в позиции $\mathbf {r} '$, и $dV'$ представляет собой бесконечно малый элемент объема, $$dq'=\rho ({\boldsymbol {r'}})\,dV'.$$

Сила на небольшом испытательном заряде $q$ на позиции ${\boldsymbol {r}}$ в вакууме определяется интегралом по распределению заряда $$\mathbf {F} (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}\int dq'{\frac {\mathbf {r} -\mathbf {r'} }{|\mathbf {r} -\mathbf {r'} |^{3}}}.$$

Версия закона Кулона о «непрерывном заряде» никогда не должна применяться к местам, для которых $|\mathbf {r} -\mathbf {r'} |=0$ потому что это местоположение будет напрямую перекрываться с местоположением заряженной частицы (например, электрона или протона), что не является допустимым местоположением для классического анализа электрического поля или потенциала. В действительности заряд всегда дискретен, и предположение о «непрерывном заряде» — это всего лишь приближение, которое не должно допускать $|\mathbf {r} -\mathbf {r'} |=0$ быть проанализированы.

Постоянная Кулона

Константа пропорциональности, ${\frac {1}{4\pi \varepsilon _{0}}}$, в законе Кулона: $$\mathbf {F} _{1}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{{\hat {\mathbf {r} }}_{12} \over {|\mathbf {r} _{12}|}^{2}}$$является следствием исторического выбора единиц измерения. Константа $\varepsilon _{0}$ – электрическая проницаемость вакуума . Использование CODATA 2018. рекомендованного значения для $\varepsilon _{0}$, постоянная Кулона является $$k_{\text{e}}={\frac {1}{4\pi \varepsilon _{0}}}=8.987\,551\,792\,3\,(14)\times 10^{9}\ \mathrm {N{\cdot }m^{2}{\cdot }C^{-2}} .$$

Ограничения

Для справедливости закона обратных квадратов Кулона необходимо выполнение трех условий:

1. Заряды должны иметь сферически-симметричное распределение (например, точечные заряды или заряженная металлическая сфера).
2. Начисления не должны перекрываться (например, это должны быть отдельные точечные начисления).
3. Заряды должны быть стационарными относительно неускоряющейся системы отсчета.

Последнее из них известно как электростатическое приближение . Когда происходит движение, вводится дополнительный фактор, который изменяет силу, действующую на два объекта. Эта дополнительная часть силы называется магнитной силой. При медленном движении магнитная сила минимальна, и закон Кулона все еще можно считать приблизительно правильным. Однако более точным приближением в этом случае является сила Вебера . Когда заряды движутся быстрее относительно друг друга или возникают ускорения, уравнения Максвелла и Эйнштейна теорию относительности необходимо учитывать .

Электрическое поле

Основная статья: Электрическое поле

Если два заряда имеют одинаковый знак, электростатическая сила между ними отталкивает; если они имеют разные знаки, сила между ними притягивается.

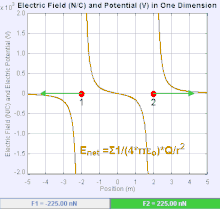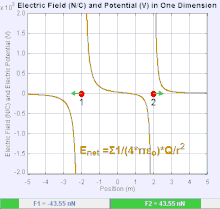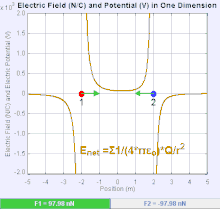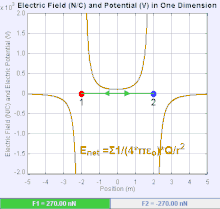
Электрическое поле — это векторное поле , которое связывает с каждой точкой пространства кулоновскую силу, действующую на единичный пробный заряд . Сила и направление силы Кулона. ${\textstyle \mathbf {F} }$ за плату ${\textstyle q_{t}}$ зависит от электрического поля ${\textstyle \mathbf {E} }$ установлено другими обвинениями, в которых он оказался, так что ${\textstyle \mathbf {F} =q_{t}\mathbf {E} }$. В простейшем случае считается, что поле создается исключительно одним точечным зарядом источника . В более общем смысле, поле может быть создано распределением зарядов, которые вносят вклад в общее состояние по принципу суперпозиции .

Если поле создается положительным точечным зарядом источника ${\textstyle q}$, направление электрического поля указывает вдоль линий, направленных радиально наружу от него, т. е. в направлении, в котором положительный точечный пробный заряд ${\textstyle q_{t}}$ будет двигаться, если его поместить в поле. Для отрицательного заряда точечного источника направление направлено радиально внутрь.

Величину электрического поля E можно получить из закона Кулона. Выбрав один из точечных зарядов в качестве источника, а другой в качестве пробного заряда, из закона Кулона следует, что величина электрического поля E, создаваемого одиночным точечным зарядом источника Q на определенном расстоянии от него r в вакуум определяется выражением $$|\mathbf {E} |=k_{\text{e}}{\frac {|q|}{r^{2}}}$$

Система n дискретных зарядов $q_{i}$ размещен в ${\textstyle \mathbf {r} _{i}=\mathbf {r} -\mathbf {r} _{i}}$ создает электрическое поле, величина и направление которого по суперпозиции равны $$\mathbf {E} (\mathbf {r} )={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}}={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{\mathbf {r} _{i} \over {|\mathbf {r} _{i}|}^{3}}$$

Атомные силы

Смотрите также: Кулоновский взрыв

Закон Кулона действует даже внутри атомов , правильно описывая силу между положительно заряженным атомным ядром и каждым из отрицательно заряженных электронов . Этот простой закон также правильно объясняет силы, которые связывают атомы вместе, образуя молекулы , и силы, которые связывают атомы и молекулы вместе, образуя твердые тела и жидкости. Обычно по мере увеличения расстояния между ионами сила притяжения и энергия связи приближаются к нулю, и ионная связь становится менее благоприятной. По мере увеличения величины противоположных зарядов энергия увеличивается, и ионная связь становится более благоприятной.

Связь с законом Гаусса

Вывод закона Гаусса из закона Кулона.

Этот раздел представляет собой отрывок из закона Гаусса § Вывод закона Гаусса из закона Кулона . [ редактировать ]

Строго говоря, закон Гаусса не может быть выведен только из закона Кулона, поскольку закон Кулона дает электрическое поле только за счет отдельного электростатического точечного заряда . Однако закон Гаусса можно доказать из закона Кулона, если дополнительно предположить, что электрическое поле подчиняется принципу суперпозиции . Принцип суперпозиции гласит, что результирующее поле представляет собой векторную сумму полей, создаваемых каждой частицей (или интеграл, если заряды равномерно распределены в пространстве).

Схема доказательства

Закон Кулона гласит, что электрическое поле, создаваемое неподвижным точечным зарядом , равно: $$\mathbf {E} (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}{\frac {\mathbf {e} _{r}}{r^{2}}}$$где

• e _r — радиальный единичный вектор ,
• r — радиус, | р | ,
• ε ₀ — электрическая постоянная ,
• q — заряд частицы, которая предполагается находящейся в начале координат .

Используя выражение из закона Кулона, мы получаем полное поле в точке r , используя интеграл для суммирования поля в точке r из-за бесконечно малых зарядов в каждой точке s в пространстве, чтобы получить $$\mathbf {E} (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho (\mathbf {s} )(\mathbf {r} -\mathbf {s} )}{|\mathbf {r} -\mathbf {s} |^{3}}}\,\mathrm {d} ^{3}\mathbf {s}$$где ρ — плотность заряда. Если взять расходимость обеих частей этого уравнения по r и воспользоваться известной теоремой

$$\nabla \cdot \left({\frac {\mathbf {r} }{|\mathbf {r} |^{3}}}\right)=4\pi \delta (\mathbf {r} )$$где δ (r) — дельта-функция Дирака , результат: $$\nabla \cdot \mathbf {E} (\mathbf {r} )={\frac {1}{\varepsilon _{0}}}\int \rho (\mathbf {s} )\,\delta (\mathbf {r} -\mathbf {s} )\,\mathrm {d} ^{3}\mathbf {s}$$

Используя « свойство просеивания » дельта-функции Дирака, мы приходим к $$\nabla \cdot \mathbf {E} (\mathbf {r} )={\frac {\rho (\mathbf {r} )}{\varepsilon _{0}}},$$что является дифференциальной формой закона Гаусса, как и хотелось.

Поскольку закон Кулона применим только к стационарным зарядам, нет оснований ожидать, что закон Гаусса будет справедливым и для движущихся зарядов, основываясь только на этом выводе. Фактически закон Гаусса справедлив для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.

Доказательство (без Дельты Дирака)

Позволять $\Omega \subseteq R^{3}$ быть ограниченным открытым множеством и $$\mathbf {E} _{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }\rho (\mathbf {r} '){\frac {\mathbf {r} -\mathbf {r} '}{\left\|\mathbf {r} -\mathbf {r} '\right\|^{3}}}\mathrm {d} \mathbf {r} '\equiv {\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$$ быть электрическим полем, причем $\rho (\mathbf {r} ')$ непрерывная функция (плотность заряда).

Это верно для всех $\mathbf {r} \neq \mathbf {r'}$ что $\nabla _{\mathbf {r} }\cdot \mathbf {e} (\mathbf {r,r'} )=0$.

Рассмотрим теперь компакт $V\subseteq R^{3}$ имеющий кусочно гладкую границу $\partial V$ такой, что $\Omega \cap V=\emptyset$. Отсюда следует, что $e(\mathbf {r,\mathbf {r} '} )\in C^{1}(V\times \Omega )$ и так, для теоремы о расходимости:

$$\oint _{\partial V}\mathbf {E} _{0}\cdot d\mathbf {S} =\int _{V}\mathbf {\nabla } \cdot \mathbf {E} _{0}\,dV$$

Но потому что $e(\mathbf {r,\mathbf {r} '} )\in C^{1}(V\times \Omega )$,

$$\mathbf {\nabla } \cdot \mathbf {E} _{0}(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega }\nabla _{\mathbf {r} }\cdot e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}=0$$ для аргумента выше ( $\Omega \cap V=\emptyset \implies \forall \mathbf {r} \in V\ \ \forall \mathbf {r'} \in \Omega \ \ \ \mathbf {r} \neq \mathbf {r'}$ а потом $\nabla _{\mathbf {r} }\cdot \mathbf {e} (\mathbf {r,r'} )=0$)

Следовательно, поток через замкнутую поверхность, создаваемый некоторой плотностью заряда снаружи (поверхности), равен нулю.

Теперь рассмотрим $\mathbf {r} _{0}\in \Omega$, и $B_{R}(\mathbf {r} _{0})\subseteq \Omega$ как сфера с центром в $\mathbf {r} _{0}$ имея $R$ как радиус (он существует, потому что $\Omega$ является открытым множеством).

Позволять $\mathbf {E} _{B_{R}}$ и $\mathbf {E} _{C}$ быть электрическим полем, созданным внутри и снаружи сферы соответственно. Затем,

$\mathbf {E} _{B_{R}}={\frac {1}{4\pi \varepsilon _{0}}}\int _{B_{R}(\mathbf {r} _{0})}e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$, $\mathbf {E} _{C}={\frac {1}{4\pi \varepsilon _{0}}}\int _{\Omega \setminus B_{R}(\mathbf {r} _{0})}e(\mathbf {r,\mathbf {r} '} ){\mathrm {d} \mathbf {r} '}$ и $\mathbf {E} _{B_{R}}+\mathbf {E} _{C}=\mathbf {E} _{0}$

$$\Phi (R)=\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{0}\cdot d\mathbf {S} =\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{B_{R}}\cdot d\mathbf {S} +\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{C}\cdot d\mathbf {S} =\oint _{\partial B_{R}(\mathbf {r} _{0})}\mathbf {E} _{B_{R}}\cdot d\mathbf {S}$$

Последнее равенство следует из наблюдения, что $(\Omega \setminus B_{R}(\mathbf {r} _{0}))\cap B_{R}(\mathbf {r} _{0})=\emptyset$и аргумент выше.

RHS — это электрический поток, создаваемый заряженной сферой, поэтому:

$$\Phi (R)={\frac {Q(R)}{\varepsilon _{0}}}={\frac {1}{\varepsilon _{0}}}\int _{B_{R}(\mathbf {r} _{0})}\rho (\mathbf {r} '){\mathrm {d} \mathbf {r} '}={\frac {1}{\varepsilon _{0}}}\rho (\mathbf {r} '_{c})|B_{R}(\mathbf {r} _{0})|$$ с $r'_{c}\in \ B_{R}(\mathbf {r} _{0})$

Где последнее равенство следует из теоремы о среднем значении для интегралов. Используя теорему сжатия и непрерывность $\rho$, получаем:

$$\mathbf {\nabla } \cdot \mathbf {E} _{0}(\mathbf {r} _{0})=\lim _{R\to 0}{\frac {1}{|B_{R}(\mathbf {r} _{0})|}}\Phi (R)={\frac {1}{\varepsilon _{0}}}\rho (\mathbf {r} _{0})$$

Вывод закона Кулона из закона Гаусса.

Строго говоря, закон Кулона не может быть выведен только из закона Гаусса, поскольку закон Гаусса не дает никакой информации относительно ротора Е ( разложение см. Гельмгольца и закон Фарадея ). Однако закон Кулона можно доказать из закона Гаусса, если дополнительно предположить, что электрическое поле от точечного заряда сферически симметрично (это предположение, как и сам закон Кулона, в точности верно, если заряд стационарен, и приблизительно верно если заряд находится в движении).

Схема доказательства

Принимая S в интегральной форме закона Гаусса за сферическую поверхность радиуса r с центром в точечном заряде Q , мы имеем $$\oint _{S}\mathbf {E} \cdot d\mathbf {A} ={\frac {Q}{\varepsilon _{0}}}$$

В предположении сферической симметрии подынтегральная функция является константой, которую можно вынести из интеграла. Результат $$4\pi r^{2}{\hat {\mathbf {r} }}\cdot \mathbf {E} (\mathbf {r} )={\frac {Q}{\varepsilon _{0}}}$$где r̂ — единичный вектор, направленный радиально от заряда. Опять же, согласно сферической симметрии, E указывает в радиальном направлении, и поэтому мы получаем $$\mathbf {E} (\mathbf {r} )={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {\hat {\mathbf {r} }}{r^{2}}}$$что по сути эквивалентно закону Кулона. Таким образом, зависимость электрического поля по закону обратных квадратов в законе Кулона следует из закона Гаусса.

В теории относительности

Закон Кулона можно использовать, чтобы понять форму магнитного поля, создаваемого движущимися зарядами, поскольку согласно специальной теории относительности в некоторых случаях можно показать, что магнитное поле представляет собой преобразование сил, вызванных электрическим полем . Когда в истории частицы не участвует никакое ускорение, закон Кулона можно принять для любой пробной частицы в ее собственной инерциальной системе отсчета, подкрепленный аргументами симметрии при решении уравнения Максвелла , показанного выше. Закон Кулона можно расширить, чтобы заставить пробные частицы иметь ту же форму. Это предположение подтверждается законом сил Лоренца , который, в отличие от закона Кулона, не ограничивается стационарными испытательными зарядами. Учитывая, что заряд инвариантен для наблюдателя, электрические и магнитные поля равномерно движущегося точечного заряда могут, следовательно, быть получены путем преобразования Лоренца четырех сил, действующих на пробный заряд в системе отсчета заряда, заданной законом Кулона и приписывающей магнитные и электрические поля по их определениям, данным в виде Сила Лоренца . Таким образом, найденные поля для равномерно движущихся точечных зарядов имеют вид: $$\mathbf {E} ={\frac {q}{4\pi \epsilon _{0}r^{3}}}{\frac {1-\beta ^{2}}{(1-\beta ^{2}\sin ^{2}\theta )^{3/2}}}\mathbf {r}$$$$\mathbf {B} ={\frac {q}{4\pi \epsilon _{0}r^{3}}}{\frac {1-\beta ^{2}}{(1-\beta ^{2}\sin ^{2}\theta )^{3/2}}}{\frac {\mathbf {v} \times \mathbf {r} }{c^{2}}}={\frac {\mathbf {v} \times \mathbf {E} }{c^{2}}}$$где $q$ – заряд точечного источника, $\mathbf {r}$ - вектор положения от источника точки до точки в пространстве, $\mathbf {v}$ – вектор скорости заряженной частицы, $\beta$ представляет собой отношение скорости заряженной частицы к скорости света и $\theta$ это угол между $\mathbf {r}$ и $\mathbf {v}$.

Эта форма решений не обязательно подчиняется третьему закону Ньютона , как это имеет место в рамках специальной теории относительности (но без нарушения закона сохранения импульса релятивистской энергии). Обратите внимание, что выражение для электрического поля сводится к закону Кулона для нерелятивистских скоростей точечного заряда и что магнитное поле в нерелятивистском пределе (приближающемся $\beta \ll 1$) можно применить к электрическим токам, чтобы получить закон Био-Савара . Эти решения, выраженные в запаздывающем времени, также соответствуют общему решению уравнений Максвелла , заданному решениями потенциала Льенара – Вихерта , из-за справедливости закона Кулона в пределах его конкретной области применения. Также обратите внимание, что сферическая симметрия закона Гаусса для стационарных зарядов недействительна для движущихся зарядов из-за нарушения симметрии при указании направления скорости в задаче. Согласие с уравнениями Максвелла также можно проверить вручную для двух приведенных выше уравнений.

Кулоновский потенциал

Смотрите также: Электрический потенциал

Квантовая теория поля

Самая основная диаграмма Фейнмана для взаимодействия КЭД между двумя фермионами.

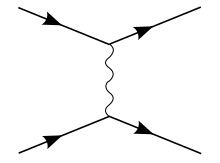
Кулоновский потенциал допускает состояния континуума (с E > 0), описывающие электрон-протонное рассеяние , а также дискретные связанные состояния, представляющие атом водорода. Его также можно получить в нерелятивистском пределе между двумя заряженными частицами следующим образом:

В борновском приближении в нерелятивистской квантовой механике амплитуда рассеяния ${\textstyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )}$ является: $${\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )-1=2\pi \delta (E_{p}-E_{p'})(-i)\int d^{3}\mathbf {r} \,V(\mathbf {r} )e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r} }$$Это следует сравнить с: $$\int {\frac {d^{3}k}{(2\pi )^{3}}}e^{ikr_{0}}\langle p',k|S|p,k\rangle$$где мы смотрим на (связанную) запись S-матрицы для двух электронов, рассеивающихся друг от друга, рассматривая один с «фиксированным» импульсом как источник потенциала, а другой рассеивается от этого потенциала.

Используя правила Фейнмана для вычисления элемента S-матрицы, в нерелятивистском пределе получаем $m_{0}\gg |\mathbf {p} |$$$\langle p',k|S|p,k\rangle |_{conn}=-i{\frac {e^{2}}{|\mathbf {p} -\mathbf {p} '|^{2}-i\varepsilon }}(2m)^{2}\delta (E_{p,k}-E_{p',k})(2\pi )^{4}\delta (\mathbf {p} -\mathbf {p} ')$$

Сравнивая с рассеянием КМ, приходится отбросить $(2m)^{2}$ поскольку они возникают из-за различных нормировок собственного состояния импульса в QFT по сравнению с QM, и получают: $$\int V(\mathbf {r} )e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r} }d^{3}\mathbf {r} ={\frac {e^{2}}{|\mathbf {p} -\mathbf {p} '|^{2}-i\varepsilon }}$$где Фурье преобразует обе части, решает интеграл и принимает $\varepsilon \to 0$ в конце даст $$V(r)={\frac {e^{2}}{4\pi r}}$$как кулоновский потенциал.

Однако эквивалентные результаты классических выводов Борна для задачи Кулона считаются строго случайными.

Кулоновский потенциал и его происхождение можно рассматривать как частный случай потенциала Юкавы , который представляет собой случай, когда обменный бозон – фотон – не имеет массы покоя.

Проверка

Эксперимент для проверки закона Кулона.

Проверить закон Кулона можно с помощью простого эксперимента. Рассмотрим две небольшие сферы массы. $m$ и одноименный заряд $q$, подвешенный на двух веревках ничтожной массы длины $l$. На каждую сферу действуют три силы: вес $mg$, натяжение каната $\mathbf {T}$ и электрическая сила $\mathbf {F}$. В равновесном состоянии:

$$\mathbf {T} \sin \theta _{1}=\mathbf {F} _{1}$$ ( 1 )

и

$$\mathbf {T} \cos \theta _{1}=mg$$ ( 2 )

Разделив ( 1 ) на ( 2 ):

$${\frac {\sin \theta _{1}}{\cos \theta _{1}}}={\frac {F_{1}}{mg}}\Rightarrow F_{1}=mg\tan \theta _{1}$$ ( 3 )

Позволять $\mathbf {L} _{1}$ — расстояние между заряженными сферами; сила отталкивания между ними $\mathbf {F} _{1}$, если предположить, что закон Кулона верен, равен

$$F_{1}={\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}$$ ( закон Кулона )

так:

$${\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}$$ ( 4 )

Если теперь разрядить одну из сфер и соприкоснуть ее с заряженной сферой, каждая из них приобретет заряд. ${\textstyle {\frac {q}{2}}}$. В состоянии равновесия расстояние между зарядами будет равно ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ а сила отталкивания между ними будет:

$$F_{2}={\frac {{({\frac {q}{2}})}^{2}}{4\pi \varepsilon _{0}L_{2}^{2}}}={\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}$$ ( 5 )

Мы знаем, что $\mathbf {F} _{2}=mg\tan \theta _{2}$ и: $${\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}=mg\tan \theta _{2}$$Разделив ( 4 ) на ( 5 ), получим:

$${\frac {\left({\cfrac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Rightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}$$ ( 6 )

Измерение углов $\theta _{1}$ и $\theta _{2}$ и расстояние между зарядами $\mathbf {L} _{1}$ и $\mathbf {L} _{2}$ достаточно, чтобы убедиться в справедливости равенства с учетом погрешности эксперимента. На практике углы может быть трудно измерить, поэтому, если длина веревок достаточно велика, углы будут достаточно малы, чтобы можно было сделать следующее приближение:

$$\tan \theta \approx \sin \theta ={\frac {\frac {L}{2}}{\ell }}={\frac {L}{2\ell }}\Rightarrow {\frac {\tan \theta _{1}}{\tan \theta _{2}}}\approx {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}$$ ( 7 )

Используя это приближение, соотношение ( 6 ) становится гораздо более простым выражением:

$${\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}$$ ( 8 )

Таким образом, проверка ограничивается измерением расстояния между зарядами и проверкой того, соответствует ли деление теоретическому значению.

См. также

• Закон Био – Савара
• Дарвин Лагранжиан
• Электромагнитная сила
• Закон Гаусса
• Метод оплаты имиджа
• Молекулярное моделирование
• Закон всемирного тяготения Ньютона , в котором используется аналогичная структура, но вместо заряда используется масса.
• Статические силы и обмен виртуальными частицами
• Эффект Казимира

Ссылки

Спавиери, Г., Гиллис, Г.Т., и Родригес, М. (2004). Физические последствия закона Кулона. Метрология, 41(5), С159–С170. дои: 10.1088/0026-1394/41/5/s06 

Связанное чтение

• Кулон, Шарль Огюстен (1788) [1785]. «Первая диссертация по электричеству и магнетизму» . История Королевской академии наук . Королевская полиграфическая компания. стр. 569–577.
• Кулон, Шарль Огюстен (1788) [1785]. «Вторая диссертация по электричеству и магнетизму» . История Королевской академии наук . Королевская полиграфическая компания. стр. 578–611.
• Кулон, Шарль Огюстен (1788) [1785]. «Третья диссертация по электричеству и магнетизму» . История Королевской академии наук . Королевская полиграфическая компания. стр. 612–638.
• Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Прентис Холл. ISBN  978-0-13-805326-0 .
• Тамм, Игорь Евгеньевич (1979) [1976]. Основы теории электричества (9-е изд.). Москва: Мир. стр. 23–27 .
• Типлер, Пол А.; Моска, Джин (2008). Физика для ученых и инженеров (6-е изд.). Нью-Йорк: WH Freeman and Company. ISBN  978-0-7167-8964-2 . LCCN   2007010418 .
• Янг, Хью Д.; Фридман, Роджер А. (2010). Университетская физика Сирса и Земанского: с современной физикой (13-е изд.). Аддисон-Уэсли (Пирсон). ISBN  978-0-321-69686-1 .

Внешние ссылки

• Закон Кулона в проекте PHYSNET
• Электричество и атом. Архивировано 21 февраля 2009 г. в Wayback Machine — глава из онлайн-учебника.
• Игра-лабиринт для изучения закона Кулона — игра, созданная с помощью программного обеспечения Molecular Workbench.
• Электрические заряды, поляризация, электрическая сила, закон Кулона Уолтер Левин, 8.02 Электричество и магнетизм, весна 2002 г.: Лекция 1 (видео). MIT OpenCourseWare. Лицензия: Creative Commons с указанием авторства, некоммерческое распространение.