Ректифицированные 5-кубики
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Октябрь 2022 г. ) |
 5-куб | 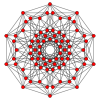 Ректифицированный 5-куб |  Биректифицированный 5-куб Биректифицированный 5-ортоплекс | ||
 5-ортоплекс |  Выпрямленный 5-ортоплекс | |||
| Ортогональные проекции в A 5 плоскости Кокстера | ||||
|---|---|---|---|---|
В пятимерной геометрии выпрямленный 5-куб — это выпуклый однородный 5-многогранник , являющийся спрямлением правильного 5-куба .
Существует 5 степеней ректификации 5-многогранника, нулевая здесь — 5-куб , а 4-я и последняя — 5-ортоплекс . Вершины выпрямленного 5-куба расположены в центрах ребер 5-куба. Вершины биректифицированного 5-куба расположены в центрах квадратных граней 5-куба.
Ректифицированный 5-куб
[ редактировать ]| Ректифицированный 5-куб пентеракт ректификованный (рин) | ||
|---|---|---|
| Тип | однородный 5-многогранник | |
| Символ Шлефли | г {4,3,3,3} | |
| Диаграмма Кокстера | ||
| 4-ликий | 42 | 10 32 |
| Клетки | 200 | 40 160 |
| Лица | 400 | 80 320 |
| Края | 320 | |
| Вершины | 80 | |
| Вершинная фигура |  Тетраэдральная призма | |
| Группа Коксетера | Б 5 , [4,3 3 ], заказать 3840 | |
| Двойной | ||
| Базовая точка | (0,1,1,1,1,1)√2 | |
| Окружность | кврт(2) = 1,414214 | |
| Характеристики | выпуклый , изогональный | |
Альтернативные названия
[ редактировать ]- Ректифицированный пентеракт (аббревиатура: рин) (Джонатан Бауэрс)
Строительство
[ редактировать ]Выпрямленный 5-куб можно построить из 5-куба , обрезав его вершины в середине ребер.
Координаты
[ редактировать ]Декартовы координаты вершин выпрямленного 5-куба с длиной ребра задается всеми перестановками:
Изображения
[ редактировать ]| Самолет Коксетера | Б 5 | Б 4 / Д 5 | Б 3 / Д 4 / А 2 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [10] | [8] | [6] |
| Самолет Коксетера | BБ2 | AА3 | |
| График | 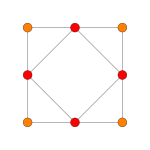 |  | |
| Двугранная симметрия | [4] | [4] |
Биректифицированный 5-куб
[ редактировать ]| Биректифицированный 5-куб биректифицированный пентеракт (нит) | ||
|---|---|---|
| Тип | однородный 5-многогранник | |
| Символ Шлефли | 2р{4,3,3,3} | |
| Диаграмма Кокстера | ||
| 4-ликий | 42 | 10 32 |
| Клетки | 280 | 40 160 80 |
| Лица | 640 | 320 320 |
| Края | 480 | |
| Вершины | 80 | |
| Вершинная фигура |  {3}×{4} | |
| Группа Коксетера | Б 5 , [4,3 3 ], заказать 3840 Д 5 , [3 2,1,1 ], приказ 1920 г. | |
| Двойной | ||
| Базовая точка | (0,0,1,1,1,1)√2 | |
| Окружность | кврт(3/2) = 1,224745 | |
| Характеристики | выпуклый , изогональный | |
ЭЛ Эльте идентифицировал его в 1912 году как полуправильный многогранник, определив его как Cr 5. 2 как второе исправление 5-мерного перекрестного многогранника .
Альтернативные названия
[ редактировать ]- Биректифицированный 5-куб/пентеракт
- Биректифицированный пентакросс/5-ортоплекс/триаконтидитерон
- Пентерактитриаконтидитерон (аббревиатура: нит) (Джонатан Бауэрс)
- Ректифицированный 5-демикуб/демипентеракт
Конструкция и координаты
[ редактировать ]Биректифицированный 5-куб можно построить путем биректификации вершин 5-куба в точках длины ребра.
Все декартовы координаты вершин биректифицированного 5-куба с длиной ребра 2 являются перестановками:
Изображения
[ редактировать ]| Самолет Коксетера | Б 5 | Б 4 / Д 5 | Б 3 / Д 4 / А 2 |
|---|---|---|---|
| График |  |  | 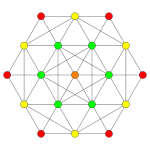 |
| Двугранная симметрия | [10] | [8] | [6] |
| Самолет Коксетера | BБ2 | AА3 | |
| График |  | 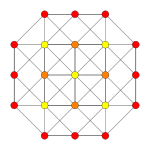 | |
| Двугранная симметрия | [4] | [4] |
Связанные многогранники
[ редактировать ]| Дим. | 2 | 3 | 4 | 5 | 6 | 7 | 8 | н |
|---|---|---|---|---|---|---|---|---|
| Имя | т{4} | г{4,3} | 2т{4,3,3} | 2р{4,3,3,3} | 3т{4,3,3,3,3} | 3р{4,3,3,3,3,3} | 4т{4,3,3,3,3,3,3} | ... |
| Коксетер диаграмма | ||||||||
| Изображения |  |   |   |   |   |   |   | |
| Фасеты | {3} {4} | т{3,3} т{3,4} | г {3,3,3} г {3,3,4} | 2т{3,3,3,3} 2т{3,3,3,4} | 2р{3,3,3,3,3} 2р{3,3,3,3,4} | 3т{3,3,3,3,3,3} 3т{3,3,3,3,3,4} | ||
| Вертекс фигура | ( )v( ) |  { }×{ } |  { }v{ } |  {3}×{4} |  {3}v{4} | {3,3}×{3,4} | {3,3}v{3,4} |
Связанные многогранники
[ редактировать ]Эти многогранники являются частью 31 однородного политера, порожденного из правильного 5-куба или 5-ортоплекса .
| Многогранники B5 |
|---|
Примечания
[ редактировать ]Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «5D однородные многогранники (политеры)» . о3х3о3о4о - рин, о3о3х3о4о - нит

































