Алгебра Гейтинга

В математике алгебра Гейтинга (также известная как псевдобулева алгебра) ) представляет собой ограниченную решетку (с операциями соединения и встречи, записанными ∨ и ∧, а также с наименьшим элементом 0 и наибольшим элементом 1), оснащенную бинарной операцией a → b импликации такой , что ( c ∧ a ) ≤ b эквивалентно c ≤ ( а → б ). С логической точки зрения, A → B по этому определению является самым слабым утверждением, для которого modus ponens , правило вывода A → B , A ⊢ B , является правильным. Подобно булевым алгебрам , алгебры Гейтинга образуют аксиоматизируемое многообразие с конечным числом уравнений. Алгебры Гейтинга были введены Арендом Хейтингом ( 1930 ) для формализации интуиционистской логики .

Гейтинговые алгебры являются дистрибутивными решетками . Каждая булева алгебра является гейтинговой алгеброй, когда a → b определяется как ¬ a ∨ b , как и любая полная дистрибутивная решетка, удовлетворяющая одностороннему бесконечному дистрибутивному закону, когда a → b считается супремумом множества всех c для который c ∧ a ≤ b . В конечном случае каждая непустая дистрибутивная решетка, в частности каждая непустая конечная цепь , автоматически является полной и вполне дистрибутивной и, следовательно, является алгеброй Гейтинга.

Из определения следует, что 1 ≤ 0 → a , что соответствует интуитивному предположению, что любое предложение a подразумевает противоречие 0. Хотя операция отрицания ¬a не является частью определения, ее можно определить как a → 0. Интуитивно понятное Содержание ¬a — это утверждение, что предположение о приведет к противоречию. Из определения следует, что a ∧ ¬ a = 0. Далее можно показать, что a ≤ ¬¬ a , хотя обратное, ¬¬ a ≤ a , в общем случае неверно, то есть исключение двойного отрицания в общем случае не выполняется. в алгебре Гейтинга.

Алгебры Гейтинга обобщают булевы алгебры в том смысле, что булевы алгебры - это в точности алгебры Гейтинга, удовлетворяющие условию a ∨ ¬ a = 1 ( исключенное среднее ), что эквивалентно ¬¬ a = a . Эти элементы гейтинговой алгебры H формы ¬a составляют булеву решетку, но, вообще говоря, это не ( см подалгебра H . ниже ).

Алгебры Гейтинга служат алгебраическими моделями пропозициональной интуиционистской логики точно так же, как булевы алгебры моделируют пропозициональную классическую логику. . Внутренняя логика элементарного топоса основана на алгебре Гейтинга подобъектов терминального объекта 1, упорядоченных по включению, что эквивалентно морфизмам от 1 к классификатору подобъектов Ω.

Открытые множества любого топологического пространства образуют полную алгебру Гейтинга . Таким образом, полные алгебры Гейтинга становятся центральным объектом изучения бессмысленной топологии .

Любая алгебра Гейтинга, набор ненаибольших элементов которой имеет наибольший элемент (и образует другую алгебру Гейтинга), является подпрямо неприводимой , следовательно, каждую алгебру Гейтинга можно сделать подпрямо неприводимой путем присоединения нового наибольшего элемента. Отсюда следует, что даже среди конечных алгебр Гейтинга существует бесконечно много подпрямо неприводимых, из которых никакие две не имеют одинаковой эквациональной теории . Следовательно, ни одно конечное множество конечных алгебр Гейтинга не может предоставить все контрпримеры к незаконам алгебры Гейтинга. Это резко контрастирует с булевыми алгебрами, у которых единственной подпрямо неприводимой является двухэлементная алгебра, которая, следовательно, сама по себе достаточна для всех контрпримеров к незаконам булевой алгебры, основы для метода решения простой таблицы истинности . Тем не менее, можно решить , справедливо ли уравнение для всех алгебр Гейтинга.

Алгебры Гейтинга реже называют псевдобулевыми алгебрами . или даже решетки Брауэра , хотя последний термин может обозначать двойное определение, или иметь несколько более общий смысл.

Формальное определение

Алгебра Гейтинга H — это ограниченная решетка такая, что для всех a и b в H существует наибольший элемент x из H такой, что

$a\wedge x\leq b.$

Этот элемент является относительным псевдодополнением a b относительно и обозначается a → b . Мы пишем 1 и 0 для самого большого и самого маленького элемента H соответственно.

В любой алгебре Гейтинга псевдодополнение ¬ a любого элемента a определяется установкой ¬ a = ( a → 0). По определению, $a\wedge \lnot a=0$, а ¬a — самый большой элемент, обладающий этим свойством. Однако в целом не верно, что $a\vee \lnot a=1$, таким образом, ¬ является лишь псевдодополнением, а не истинным дополнением , как это было бы в булевой алгебре.

Полная алгебра Гейтинга — это алгебра Гейтинга, которая представляет собой полную решетку .

Подалгеброй 0 гейтинговой алгебры H называется подмножество H1 _{содержащее} в H, и 1 и замкнутое относительно операций ∧, ∨ и →. Отсюда следует, что оно замкнуто и при ¬. Подалгебра превращается в алгебру Гейтинга с помощью индуцированных операций.

Альтернативные определения

Теоретико-категорное определение

Алгебра Гейтинга $H$ представляет собой ограниченную решетку, в которой есть все экспоненциальные объекты .

Решетка $H$ рассматривается как категория , в которой встретиться, $\wedge$, это продукт . Экспоненциальное условие означает, что для любых объектов $Y$ и $Z$ в $H$ экспоненциальная $Z^{Y}$ однозначно существует как объект в $H$.

Импликация Хейтинга (часто записываемая с использованием $\Rightarrow$ или $\multimap$ во избежание путаницы, такой как использование $\to$ для обозначения функтора ) является просто экспонентой: $Y\Rightarrow Z$ является альтернативным обозначением для $Z^{Y}$. Из определения экспоненты мы получаем следующее следствие ( $\Rightarrow :H\times H\to H$) правосопряжён к пересечению ( $\wedge :H\times H\to H$). Это дополнение можно записать как $(-\wedge Y)\dashv (Y\Rightarrow -)$ или более полно как: $$(-\wedge Y):H{\stackrel {\longrightarrow }{\underset {\longleftarrow }{\top }}}H:(Y\Rightarrow -)$$

Теоретико-решеточные определения

Эквивалентное определение гейтинговых алгебр можно дать, рассматривая отображения:

${\begin{cases}f_{a}\colon H\to H\\f_{a}(x)=a\wedge x\end{cases}}$

для некоторого фиксированного a в H . Ограниченная решетка H является гейтинговой алгеброй тогда и только тогда, когда каждое отображение f _a является нижним сопряжением монотонной связности Галуа . В этом случае соответствующее верхнее сопряженное g _a задается выражением g _a ( x ) = a → x , где → определяется, как указано выше.

Еще одно определение — это остаточная решетка , моноидная операция которой равна ∧. Тогда единица моноида должна быть верхним элементом 1. Коммутативность этого моноида подразумевает, что два остатка совпадают при a → b .

Ограниченная решетка с операцией импликации

Учитывая ограниченную решетку A с наибольшими и наименьшими элементами 1 и 0 и бинарную операцию →, они вместе образуют алгебру Гейтинга тогда и только тогда, когда выполняются следующие условия:

1. $a\to a=1$
2. $a\wedge (a\to b)=a\wedge b$
3. $b\wedge (a\to b)=b$
4. $a\to (b\wedge c)=(a\to b)\wedge (a\to c)$

где уравнение 4 представляет собой закон распределения →.

Характеристика с использованием аксиом интуиционистской логики

Эта характеристика алгебр Гейтинга делает немедленным доказательство основных фактов, касающихся связи между интуиционистским исчислением высказываний и алгебрами Гейтинга. (Эти факты см. в разделах « Доказуемые тождества » и « Универсальные конструкции ».) Следует подумать об элементе $\top$ как интуитивно означающее «доказуемо верно». Сравните с аксиомами в Интуиционистской логике#Аксиоматизация ).

Дан набор A с тремя двоичными операциями →, ∧ и ∨ и двумя выделенными элементами. $\bot$ и $\top$, то A является гейтинговой алгеброй для этих операций (и отношение ≤ определяется условием, что $a\leq b$ когда а → б = $\top$ выполняются следующие условия ) тогда и только тогда, когда для любых элементов x , y и z из A :

1. ${\mbox{If }}x\leq y{\mbox{ and }}y\leq x{\mbox{ then }}x=y,$
2. ${\mbox{If }}\top \leq y,{\mbox{ then }}y=\top ,$
3. $x\leq y\to x,$
4. $x\to (y\to z)\leq (x\to y)\to (x\to z),$
5. $x\land y\leq x,$
6. $x\land y\leq y,$
7. $x\leq y\to (x\land y),$
8. $x\leq x\lor y,$
9. $y\leq x\lor y,$
10. $x\to z\leq (y\to z)\to (x\lor y\to z),$
11. $\bot \leq x.$

Наконец, мы определяем ¬ x как x → $\bot$.

Условие 1 говорит о том, что должны быть идентифицированы эквивалентные формулы. Условие 2 гласит, что доказуемо истинные формулы замкнуты относительно modus ponens . условия 3 и 4 являются Тогда условиями. Условия 5, 6 и 7 являются и условиями. Условия 8, 9 и 10 являются или условиями. Условие 11 является ложным .

Конечно, если бы для логики был выбран другой набор аксиом, мы могли бы соответствующим образом изменить наш.

Примеры

алгебра Свободная Гейтинга над одним образующим (она же решетка Ригера – Нисимуры)

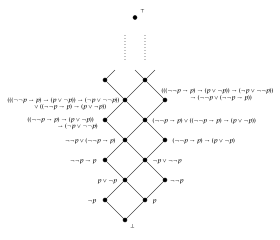
• Каждая булева алгебра является гейтинговой алгеброй, где p → q задано формулой ¬ p ∨ q .
• Каждое полностью упорядоченное множество , имеющее наименьший элемент 0 и наибольший элемент 1, является алгеброй Гейтинга (если рассматривать его как решетку). В этом случае p → q равно 1, когда p≤q , и q в противном случае.
• Простейшая алгебра Гейтинга, которая еще не является булевой алгеброй, — это полностью упорядоченное множество {0, ⁠ 1 / 2 ⁠ , 1} (рассматривается как решетка), что дает операции:

  $a\land b$ б а 0 ⁠ 1 / 2 ⁠ 1 0 0 0 0 ⁠ 1 / 2 ⁠ 0 ⁠ 1 / 2 ⁠ ⁠ 1 / 2 ⁠ 1 0 ⁠ 1 / 2 ⁠ 1

  $a\lor b$ б а 0 ⁠ 1 / 2 ⁠ 1 0 0 ⁠ 1 / 2 ⁠ 1 ⁠ 1 / 2 ⁠ ⁠ 1 / 2 ⁠ ⁠ 1 / 2 ⁠ 1 1 1 1 1

  a → b б а 0 ⁠ 1 / 2 ⁠ 1 0 1 1 1 ⁠ 1 / 2 ⁠ 0 1 1 1 0 ⁠ 1 / 2 ⁠ 1

  а ¬ a 0 1 ⁠ 1 / 2 ⁠ 0 1 0

  В этом примере это ⁠ 1 / 2 ⁠ ∨¬ ⁠ 1 / 2 ⁠ = ⁠ 1 / 2 ⁠ ∨( ⁠ 1 / 2 ⁠ → 0) = ⁠ 1 / 2 ⁠ ∨0 = ⁠ 1/2 ⁠ фальсифицирует . закон исключенного третьего

• Каждая топология представляет собой полную алгебру Гейтинга в форме решетки открытых множеств . В этом случае элемент A → B является внутренностью объединения A ^с и B , где A ^с обозначает дополнение открытого множества A . Не все полные алгебры Гейтинга имеют такую ​​форму. Эти вопросы изучаются в бессмысленной топологии , где полные алгебры Гейтинга также называются фреймами или локалями .
• Каждая внутренняя алгебра представляет собой алгебру Гейтинга в виде решетки открытых элементов. Каждая алгебра Гейтинга имеет такую ​​форму, поскольку алгебра Гейтинга может быть дополнена до булевой алгебры, если взять ее свободное булево расширение как ограниченную дистрибутивную решетку и затем рассматривать ее как обобщенную топологию в этой булевой алгебре.
• Алгебра Линденбаума пропозициональной интуиционистской логики является алгеброй Гейтинга.
• Глобальные элементы классификатора подобъектов Ω элементарного топоса образуют алгебру Гейтинга; это алгебра Гейтинга истинностных значений интуиционистской логики высшего порядка, индуцированной топосом. В более общем смысле, набор подобъектов любого объекта X в топосе образует алгебру Гейтинга.
• Алгебры Лукасевича–Мойсила (LM _n ) также являются алгебрами Гейтинга для любого n (но они не являются MV-алгебрами при n ≥ 5 ).

Характеристики

Общие свойства

Порядок $\leq$ на гейтинговой алгебре H можно восстановить с помощью операции → следующим образом: для любых элементов a , b из H , $a\leq b$ тогда и только тогда, когда a → b = 1.

В отличие от некоторых многозначных логик , алгебры Гейтинга разделяют следующее свойство с булевыми алгебрами: если отрицание имеет фиксированную точку (т. е. ¬ a = a для некоторого a ), то алгебра Гейтинга является тривиальной одноэлементной алгеброй Гейтинга.

Доказуемые личности

Учитывая формулу $F(A_{1},A_{2},\ldots ,A_{n})$ исчисления высказываний (с использованием, помимо переменных, связок $\land ,\lor ,\lnot ,\to$и константы 0 и 1), это факт, доказанный на ранних этапах любого исследования алгебр Гейтинга, что следующие два условия эквивалентны:

1. Формула F доказуемо верна в интуиционистском исчислении высказываний.
2. Личность $F(a_{1},a_{2},\ldots ,a_{n})=1$ верно для любой гейтинговой алгебры H и любых элементов $a_{1},a_{2},\ldots ,a_{n}\in H$.

Мета-импликация 1 ⇒ 2 чрезвычайно полезна и является основным практическим методом доказательства тождеств в гейтинговых алгебрах. На практике в таких доказательствах часто используют теорему дедукции .

Поскольку для любых a и b в гейтинговой алгебре H имеем $a\leq b$ тогда и только тогда, когда a → b следует = 1, из 1 ⇒ 2 , что всякий раз, когда формула F → G доказуемо истинна, мы имеем $F(a_{1},a_{2},\ldots ,a_{n})\leq G(a_{1},a_{2},\ldots ,a_{n})$ для любой алгебры Гейтинга H и любых элементов $a_{1},a_{2},\ldots ,a_{n}\in H$. (Из теоремы о дедукции следует, что F → G доказуемо (безусловно) тогда и только тогда, когда G доказуемо из F , то есть если G является доказуемым следствием F .) В частности, если F и G доказуемо эквивалентны, затем $F(a_{1},a_{2},\ldots ,a_{n})=G(a_{1},a_{2},\ldots ,a_{n})$, поскольку ≤ — отношение порядка.

1 ⇒ 2 можно доказать, исследовав логические аксиомы системы доказательства и проверив, что их значение равно 1 в любой алгебре Гейтинга, а затем проверив, что применение правил вывода к выражениям со значением 1 в алгебре Гейтинга приводит к выражения со значением 1. Например, давайте выберем систему доказательства, имеющую modus ponens в качестве единственного правила вывода и чьи аксиомы являются аксиомами в стиле Гильберта, приведенными в Интуиционистская логика # Аксиоматизация . Тогда факты, подлежащие проверке, непосредственно следуют из аксиомного определения гейтинговых алгебр, данного выше.

1 ⇒ 2 также обеспечивает метод доказательства того, что некоторые пропозициональные формулы, хотя и являются тавтологиями в классической логике, не могут быть доказаны в интуиционистской логике высказываний. Чтобы доказать, что некоторая формула $F(A_{1},A_{2},\ldots ,A_{n})$ недоказуемо, достаточно указать гейтингову алгебру H и элементы $a_{1},a_{2},\ldots ,a_{n}\in H$ такой, что $F(a_{1},a_{2},\ldots ,a_{n})\neq 1$.

Если же хочется избежать упоминания о логике, то на практике возникает необходимость доказать в виде леммы вариант теоремы о дедукции, справедливый для гейтинговых алгебр: для любых элементов a , b и c гейтинговой алгебры H имеем $(a\land b)\to c=a\to (b\to c)$.

Подробнее о метаимпликации 2 ⇒ 1 см. ниже в разделе « Универсальные конструкции ».

Дистрибутивность

Гейтинговые алгебры всегда дистрибутивны . В частности, у нас всегда есть тождества

1. $a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)$
2. $a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c)$

Закон распределения иногда называют аксиомой, но на самом деле он следует из существования относительных псевдодополнений. Причина в том, что, будучи нижним сопряженным связности Галуа , $\wedge$ сохраняет все существующие супремы . Дистрибутивность, в свою очередь, — это всего лишь сохранение бинарных супремумов посредством $\wedge$.

По аналогичному аргументу следующий бесконечный дистрибутивный закон в любой полной алгебре Гейтинга выполняется :

$x\wedge \bigvee Y=\bigvee \{x\wedge y\mid y\in Y\}$

для любого элемента x в H и любого подмножества Y из H . И наоборот, любая полная решетка, удовлетворяющая указанному выше бесконечному дистрибутивному закону, является полной алгеброй Гейтинга с

$a\to b=\bigvee \{c\mid a\land c\leq b\}$

являющаяся его относительной операцией псевдодополнения.

Обычные и дополненные элементы

Элемент x гейтинговой алгебры H называется регулярным , если выполняется любое из следующих эквивалентных условий:

1. х = ¬¬ х .
2. x = ¬ y для некоторого y из H .

Эквивалентность этих условий можно просто сформулировать как тождество ¬¬¬x = ¬x , для всех x в H. действительное

Элементы x и y гейтинговой алгебры H называются дополнениями друг к другу, если x ∧ y = 0 и x ∨ y = 1. Если он существует, любой такой y уникален и фактически должен быть равен ¬ x . Мы называем элемент x дополненным, если он допускает дополнение. Это правда, что если x дополняется, то и ¬x дополняется , и тогда x и ¬x дополняют друг друга. Однако, что сбивает с толку, даже если x не дополняется, ¬ x , тем не менее, может иметь дополнение (не равное x ). В любой алгебре Гейтинга элементы 0 и 1 являются дополнениями друг к другу. Например, возможно, что ¬ x равен 0 для каждого x, отличного от 0, и 1, если x = 0, и в этом случае 0 и 1 являются единственными правильными элементами.

Любой дополняемый элемент гейтинговой алгебры регулярен, хотя обратное, вообще говоря, неверно. В частности, 0 и 1 всегда регулярны.

Для любой гейтинговой алгебры H следующие условия эквивалентны:

1. H — булева алгебра ;
2. каждый x в H регулярен;
3. каждый x в H дополняется.

В этом случае элемент a → b равен ¬ a ∨ b .

Регулярные (соответственно дополняемые) элементы любой гейтинговой алгебры H образуют булеву алгебру H _reg (соответственно H _comp ), в которой операции ∧, ¬ и →, а также константы 0 и 1 совпадают с операциями H . В случае H _comp операция ∨ также та же самая, следовательно, H _comp является подалгеброй H . Однако в общем случае H _reg не будет подалгеброй H , поскольку ее операция соединения ∨ _reg может отличаться от ∨. Для x , y ∈ H _reg . имеем x ∨ _reg y = ¬(¬ x ∧ ¬ y ) Ниже приведены необходимые и достаточные условия для _{∨ reg} совпадения с ∨.

Законы де Моргана в алгебре Гейтинга

один из двух законов Де Моргана В каждой алгебре Гейтинга выполняется , а именно

$\forall x,y\in H:\qquad \lnot (x\vee y)=\lnot x\wedge \lnot y.$

Однако другой закон Де Моргана не всегда выполняется. Вместо этого мы имеем слабый закон де Моргана:

$\forall x,y\in H:\qquad \lnot (x\wedge y)=\lnot \lnot (\lnot x\vee \lnot y).$

Следующие утверждения эквивалентны для всех гейтинговых алгебр H :

1. H удовлетворяет обоим законам Де Моргана:
2. $\lnot (x\wedge y)=\lnot x\vee \lnot y{\mbox{ for all }}x,y\in H,$
3. $\lnot (x\wedge y)=\lnot x\vee \lnot y{\mbox{ for all regular }}x,y\in H,$
4. $\lnot \lnot (x\vee y)=\lnot \lnot x\vee \lnot \lnot y{\mbox{ for all }}x,y\in H,$
5. $\lnot \lnot (x\vee y)=x\vee y{\mbox{ for all regular }}x,y\in H,$
6. $\lnot (\lnot x\wedge \lnot y)=x\vee y{\mbox{ for all regular }}x,y\in H,$
7. $\lnot x\vee \lnot \lnot x=1{\mbox{ for all }}x\in H.$

Условие 2 — это еще один закон Де Моргана. Условие 6 гласит, что операция соединения ∨ _reg на булевой алгебре H _reg регулярных элементов группы H совпадает с операцией ∨ группы H . Условие 7 гласит, что каждый регулярный элемент дополняем, т. е. H _reg = H _comp .

Докажем эквивалентность. Очевидно, что мета-импликации 1 ⇒ 2, 2 ⇒ 3 и 4 ⇒ 5 тривиальны. Более того, 3 ⇔ 4 и 5 ⇔ 6 просто следуют из первого закона Де Моргана и определения регулярных элементов. Мы покажем, что 6 ⇒ 7 , взяв ¬ x и ¬¬ x вместо x и y в 6 и воспользовавшись тождеством a ∧ ¬ a = 0. Заметим, что 2 ⇒ 1 следует из первого закона Де Моргана, а 7 ⇒ 6. является результатом того, что операция соединения ∨ на подалгебре H _comp является не чем иным, как ограничением ∨ на H _comp с учетом данных нами характеристик условий 6 и 7. Мета-импликация 5 ⇒ 2 является тривиальным следствием слабого Закон де Моргана, берущий ¬x и ¬y вместо x и y в 5.

Алгебры Гейтинга, удовлетворяющие указанным выше свойствам, связаны с логикой Де Моргана так же, как алгебры Гейтинга в целом связаны с интуиционистской логикой.

Морфизмы алгебры Гейтинга

Определение

Учитывая две алгебры Гейтинга H ₁ и H ₂ и отображение f : H ₁ → H ₂ , мы говорим, что ƒ является морфизмом алгебр Гейтинга, если для любых элементов x и y из H ₁ имеем:

1. $f(0)=0,$
2. $f(x\land y)=f(x)\land f(y),$
3. $f(x\lor y)=f(x)\lor f(y),$
4. $f(x\to y)=f(x)\to f(y),$

Из любого из трех последних условий (2, 3 или 4) следует, что f — возрастающая функция, то есть f ( x ) ⩽ f ( y ) всякий раз, когда x ⩽ y .

Предположим, что H ₁ и H ₂ — структуры с операциями →, ∧, ∨ (и, возможно, ¬) и константами 0 и 1, а f — сюръективное отображение из H ₁ в H ₂ со свойствами с 1 по 4, указанными выше. Тогда если H ₁ является гейтинговой алгеброй, то и H ₂ тоже является гейтинговой . Это следует из характеристики гейтинговых алгебр как ограниченных решеток (которые рассматриваются как алгебраические структуры, а не как частично упорядоченные множества) с операцией →, удовлетворяющей определенным тождествам.

Характеристики

Тождественное отображение f ( x ) = x из любой алгебры Гейтинга в себя является морфизмом, а композиция g ∘ f любых двух морфизмов f и g является морфизмом. Следовательно, алгебры Гейтинга образуют категорию .

Примеры

Для гейтинговой алгебры H и любой подалгебры H ₁ отображение включения i : H ₁ → H является морфизмом.

Для любой гейтинговой алгебры H отображение x ↦ ¬¬x определяет морфизм из H на булеву алгебру ее регулярных Hreg _{элементов} . В общем, это не морфизм H в себя, поскольку операция соединения H _reg может отличаться от операции H .

Коэффициенты

Пусть H — гейтинговая алгебра F ⊆ H. и Мы называем F фильтром если на H, он удовлетворяет следующим свойствам:

1. $1\in F,$
2. ${\mbox{If }}x,y\in F{\mbox{ then }}x\land y\in F,$
3. ${\mbox{If }}x\in F,\ y\in H,\ {\mbox{and }}x\leq y{\mbox{ then }}y\in F.$

Пересечение любого набора фильтров на H снова является фильтром. Следовательно, для любого подмножества S из H существует наименьший фильтр, S. содержащий фильтром сгенерированным S. , Мы называем это Если S пусто, F = {1}. В противном случае F равно множеству x в H таких, что существуют y ₁ , y ₂ , ..., y _n ∈ S такие, что y ₁ ∧ y ₂ ∧ ... ∧ y _n ≤ x .

Если H — алгебра Гейтинга, а F — фильтр на H , мы определяем отношение ~ на H следующим образом: мы пишем x ~ y всякий раз, когда x → y и y → x оба принадлежат F . Тогда ~ — отношение эквивалентности ; мы пишем H / F для фактормножества . существует уникальная структура алгебры Гейтинга На H / F такая, что каноническая сюръекция p _F : H → H / F становится морфизмом алгебры Гейтинга. Гейтинга H / F фактор H F. по мы называем Алгеброй

Пусть S — подмножество гейтинговой алгебры H и пусть F — фильтр, порожденный S. , Тогда H / F удовлетворяет следующему универсальному свойству:

Для любого морфизма гейтинговых алгебр f : H → H ′, удовлетворяющего f ( y ) = 1 для каждого y ∈ S , f факторизуется однозначно через каноническую сюръекцию p _F : H → H / F . То есть существует единственный морфизм f ′ : H / F → H ′, такой, что f ′ p _F = f . морфизм f , Говорят индуцирован f что .

Пусть f : H ₁ → H ₂ — морфизм гейтинговых алгебр. Ядро представляет f f , обозначаемое ker , собой множество f ⁻¹ [{1}]. Это фильтр на H ₁ . (Следует проявлять осторожность, поскольку это определение, если оно применяется к морфизму булевых алгебр, двойственно тому, что можно было бы назвать ядром морфизма, рассматриваемого как морфизм колец.) Согласно вышесказанному, f индуцирует морфизм f ′ : H ₁ /(ker f ) → ЧАС ₂ . Это изоморфизм H ₁ /(ker f ) на подалгебру f [ H ₁ ] в H ₂ .

Универсальные конструкции

Гейтинговая алгебра пропозициональных формул от n переменных с точностью до интуиционистской эквивалентности

Мета-импликация 2 ⇒ 1 в разделе « Доказуемые тождества » доказывается, показывая, что результат следующей конструкции сам является гейтинговой алгеброй:

1. Рассмотрим множество L пропозициональных формул от переменных A ₁ , A ₂ ,... An _, .
2. Наделите L предварительным порядком ≼, определив F ≼ G, G является (интуиционистским) логическим следствием F если , то есть если G доказуемо из F . Сразу видно, что ≼ — это предзаказ.
3. Рассмотрим отношение эквивалентности F ~ G, индуцированное предпорядком F≼G. (Оно определяется как F ~ G тогда и только тогда, когда F ≼ G и G ≼ F . Фактически, ~ является отношением (интуиционистской) логической эквивалентности.)
4. Пусть H0 _/ — фактормножество L ~. Это и будет искомая алгебра Гейтинга.
5. Обозначим через [ F класс эквивалентности формулы F. ] Операции →, ∧, ∨ и ¬ определяются очевидным образом на L . Убедитесь, что для данных формул F и G классы эквивалентности [ F → G ], [ F ∧ G ], [ F ∨ G ] и [¬ F ] зависят только от [ F ] и [ G ]. Это определяет операции →, ∧, ∨ и ¬ на фактормножестве H ₀ = L /~. Далее определим 1 как класс доказуемо истинных утверждений и установим 0=[⊥].
6. Убедитесь, что H ₀ вместе с этими операциями является гейтинговой алгеброй. Мы делаем это, используя аксиоматическое определение алгебр Гейтинга. H ₀ удовлетворяет условиям THEN-1 через FALSE, поскольку все формулы данных форм являются аксиомами интуиционистской логики. MODUS-PONENS следует из того факта, что если формула ⊤→ F доказуемо истинна, где ⊤ доказуемо истинна, то F доказуемо истинна (путем применения правила вывода modus ponens). Наконец, EQUIV вытекает из того факта, что если F → ​​G и G → F оба доказуемо истинны, то F и G доказуемы друг из друга (путем применения правила вывода modus ponens), следовательно, [ F ]=[ G ] .

Как всегда при аксиоматическом определении алгебр Гейтинга, мы определяем ⩽ на H ₀ условием, что x ⩽ y тогда и только тогда, когда x → y =1. Поскольку по теореме о дедукции формула F → G доказуемо истинна тогда и только тогда, когда G доказуема из F , отсюда следует, что [ F ]≤[ G ] тогда и только тогда, когда F≼G. Другими словами, ≤ — это отношение порядка на L индуцированное предпорядком ≼ на L. /~ ,

Свободная алгебра Гейтинга на произвольном наборе образующих

Фактически предыдущую конструкцию можно провести для любого набора переменных { A _i : i ∈ I } (возможно, бесконечного). Таким образом получается свободная алгебра Гейтинга переменных { Ai _} мы снова обозначим через H0 _{, которую} . Она свободна в том смысле, что для любой гейтинговой алгебры H, заданной вместе с семейством ее элементов 〈 a _i : i ∈ I 〉, существует единственный морфизм f : H ₀ → H, удовлетворяющий f ([ A _i ]) = a _я . Единственность f нетрудно увидеть, и ее существование, по существу, вытекает из мета-импликации 1 ⇒ 2 из раздела « Доказуемые тождества » выше, в форме ее следствия, что всякий раз, когда F и G являются доказуемо эквивалентными формулами, F (〈 a _i 〉)= G (〈 a _i 〉) для любого семейства элементов 〈 a _i 〉 в H .

Гейтинговая алгебра формул, эквивалентных относительно теории T

Учитывая набор формул T в переменных { A _i }, рассматриваемых как аксиомы, ту же конструкцию можно было бы провести по отношению к отношению F ≼ G, определенному на L, чтобы означать, что G является доказуемым следствием F и множества аксиом Т. ​Обозначим HT _через полученную таким образом алгебру Гейтинга . Тогда HT ₍ удовлетворяет тому же универсальному свойству, что и H ₀ выше, но относительно гейтинговых алгебр H и семейств элементов 〈 a _i 〉, удовлетворяющих свойству, что J (〈 a _i 〉)=1 для любой аксиомы J 〈 A _i 〉 в Т. ) (Заметим, что , _HT взятый вместе с семейством своих элементов 〈[ ] _Ai 〉, сам удовлетворяет этому свойству.) Существование и единственность морфизма доказывается так же, как и для , _H0 за исключением того, что необходимо модифицировать мета-импликация 1 ⇒ 2 в « Доказуемые тождества », так что 1 читается как «доказуемо истинно из T », а 2 читается как «любые элементы a ₁ , a ₂ ,..., an _{удовлетворяющие} в H, формулам T ».

Алгебру Гейтинга HT _, фактор свободной алгебры Гейтинга H ₀ по тому же набору переменных, применяя универсальное свойство H ₀ по отношению к HT _{которую мы только что определили, можно рассматривать как} и семейству ее элементов 〈[ А _я ]〉.

Каждая алгебра Гейтинга изоморфна одной из форм H _T . Чтобы убедиться в этом, пусть H — любая гейтинговая алгебра и пусть 〈 a _i : i ∈I〉 — семейство элементов, порождающее H (например, любое сюръективное семейство). Теперь рассмотрим множество T формул J (〈 A _i 〉) от переменных 〈 A _i : i ∈I〉 таких, что J (〈 a _i 〉)=1. Тогда мы получаем морфизм f : HT _{сюръективен} → H по универсальному свойству HT _. , который, очевидно, Нетрудно показать, что f инъективно.

Сравнение с алгебрами Линденбаума

Только что приведенные нами конструкции играют по отношению к алгебрам Гейтинга совершенно аналогичную роль алгебры Линденбаума по отношению к булевым алгебрам . Фактически, алгебра Линденбаума B _T в переменных { A _i } относительно аксиом T — это просто наш H _{T ∪ T 1} , где T ₁ — множество всех формул вида ¬¬ F → F , поскольку дополнительные аксиомы T ₁ — единственные, которые необходимо добавить, чтобы сделать все классические тавтологии доказуемыми.

Алгебры Гейтинга в применении к интуиционистской логике

Если интерпретировать аксиомы интуиционистской пропозициональной логики как термины алгебры Гейтинга, то их результат будет равен наибольшему элементу, 1, в любой алгебре Гейтинга при любом присвоении значений переменным формулы. Например, ( P ∧ Q )→ P по определению псевдодополнения является наибольшим элементом x таким, что $P\land Q\land x\leq P$. Это неравенство выполняется для любого x , поэтому наибольший такой x равен 1.

правило modus ponens позволяет вывести формулу Q из формул P и P → Q. Более того , Но в любой алгебре Гейтинга, если P имеет значение 1, а P → Q имеет значение 1, то это означает, что $P\land 1\leq Q$, и так $1\land 1\leq Q$; может быть только так, что Q имеет значение 1.

Это означает, что если формула выводится из законов интуиционистской логики, будучи выведена из ее аксиом по правилу modus ponens, то она всегда будет иметь значение 1 во всех алгебрах Гейтинга при любом присвоении значений переменным формулы. . Однако можно построить алгебру Гейтинга, в которой значение закона Пирса не всегда равно 1. Рассмотрим 3-элементную алгебру {0, ⁠ 1/2 1} , ⁠ , как указано выше. Если мы назначим ⁠ 1/2 и 0 ⁠ для P для Q , то значение закона Пирса (( P → Q )→ P )→ P равно ⁠ 1/2 ​ ⁠ ​ . Отсюда следует, что закон Пирса не может быть выведен интуиционистски. см . в разделе «Изоморфизм Карри–Ховарда». Общий контекст того, что это подразумевает в теории типов ,

Обратное также можно доказать: если формула всегда имеет значение 1, то она выводится из законов интуиционистской логики, поэтому интуиционистски действительными формулами являются именно те, которые всегда имеют значение 1. Это аналогично понятию что классически действительные формулы - это те формулы, которые имеют значение 1 в двухэлементной булевой алгебре при любом возможном присвоении значений true и false переменным формулы, то есть это формулы, которые являются тавтологиями в обычном смысле таблицы истинности. Алгебра Гейтинга с логической точки зрения является тогда обобщением обычной системы значений истинности, и ее наибольший элемент 1 аналогичен «истинному». Обычная система двузначной логики представляет собой частный случай гейтинговой алгебры, причем наименьший нетривиальный, в котором единственными элементами алгебры являются 1 (истина) и 0 (ложь).

Проблемы с решением

в 1965 году показал, что проблема о том, выполняется ли данное уравнение во всех алгебрах Гейтинга Сол Крипке . Точная вычислительная сложность задачи была установлена ​​Ричардом Статманом в 1979 году, который показал, что она PSPACE-полна. и, следовательно, по крайней мере так же сложно, как решение уравнений булевой алгебры (показано Стивеном Куком в 1971 году как coNP-полное ) и предположительно значительно сложнее. Элементарная теория гейтинговых алгебр первого порядка неразрешима. Остается открытым вопрос, разрешима ли универсальная теория Хорна гейтинговых алгебр или проблема слов . Что касается проблемы слов, то известно, что алгебры Гейтинга не являются локально конечными (ни одна алгебра Гейтинга, порожденная конечным непустым множеством, не является конечной), в отличие от булевых алгебр, которые локально конечны и проблема слов которых разрешима. Неизвестно, существуют ли свободные полные алгебры Гейтинга, за исключением случая с одним генератором, когда свободная алгебра Гейтинга на одном генераторе тривиально дополняется присоединением новой вершины.

Топологическое представление и теория двойственности

Любая гейтинговая алгебра H естественно изоморфна ограниченной подрешетке L открытых множеств топологического пространства X , где импликация $U\to V$ L частью задается внутренней $(X\setminus U)\cup V$. Точнее, X — спектральное пространство простых идеалов ограниченной решетки H , а L — решетка открытых и квазикомпактных подмножеств X .

В более общем смысле, категория гейтинговых алгебр дуально эквивалентна категории гейтинговых пространств. Эту двойственность можно рассматривать как ограничение классической двойственности Стоуна ограниченных дистрибутивных решеток на (неполную) подкатегорию гейтинговых алгебр.

Альтернативно, категория алгебр Гейтинга дуально эквивалентна категории пространств Эсакиа . Это называется двойственностью Эсакии .

См. также

• Топология Александрова
• Суперинтуиционистская (или промежуточная) логика
• Список тем по булевой алгебре
• Алгебра Оккама

Ссылки

• Резерфорд, Дэниел Эдвин (1965). Введение в теорию решеток . Оливер и Бойд. OCLC   224572 .
• Ф. Борсо, Справочник по категорической алгебре 3 , В энциклопедии математики и ее приложений , Vol. 53, Издательство Кембриджского университета, 1994. ISBN   0-521-44180-3 ОСЛК   52238554
• Г. Гирц, К. Х. Хоффманн, К. Кеймель, Дж. Д. Лоусон, М. Мислов и Д. С. Скотт , Непрерывные решетки и области , В энциклопедии математики и ее приложений , Vol. 93, Издательство Кембриджского университета, 2003.
• С. Гиларди. Свободные алгебры Гейтинга как би-гейтинговые алгебры , Матем. член палаты представителей акад. наук. Канада XVI., 6: 240–244, 1992.
• Гейтинг А. (1930), «Формальные правила интуиционистской логики. I, II, III», протоколы заседаний Акад. Берлин : 42–56, 57–71, 158–169, JFM   56.0823.01 .
• Дикманн, Макс; Шварц, Нильс; Трессл, Маркус (2019). Спектральные пространства . Новые математические монографии. Том. 35. Кембридж: Издательство Кембриджского университета . дои : 10.1017/9781316543870 . ISBN  9781107146723 . S2CID   201542298 .

Внешние ссылки

• Алгебра Гейтинга в PlanetMath .