5-куб
| 5-куб пентеракт (пентеракт) | ||
|---|---|---|
| Тип | однородный 5-многогранник | |
| Символ Шлефли | {4,3,3,3} | |
| Диаграмма Кокстера | ||
| 4-ликий | 10 | тессеракты |
| Клетки | 40 | кубики |
| Лица | 80 | квадраты |
| Края | 80 | |
| Вершины | 32 | |
| Вершинная фигура | 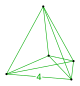 5-клеточный | |
| Группа Коксетера | Б 5 , [4,3 3 ], заказать 3840 | |
| Двойной | 5-ортоплекс | |
| Базовая точка | (1,1,1,1,1,1) | |
| Окружность | кврт(5)/2 = 1,118034 | |
| Характеристики | выпуклый , изогональный правильный , многогранник Ханнера | |
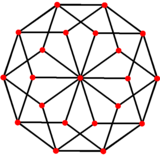
В пятимерной геометрии 5 -куб — это название пятимерного гиперкуба с 32 вершинами , 80 ребрами , 80 квадратными гранями , 40 кубическими ячейками и 10 тессеракта 4-гранями .
Он представлен символом Шлефли {4,3,3,3} или {4,3. 3 }, построенный как 3 тессеракта {4,3,3} вокруг каждого кубического гребня .
Связанные многогранники
[ редактировать ]Это часть бесконечного семейства гиперкубов . Двойственным бесконечного 5-кубу является 5-ортоплекс семейства ортоплексов .
Применение операции чередования , удаляющей чередующиеся вершины 5-куба, создает еще один однородный 5-многогранник , называемый 5-демикубом , который также является частью бесконечного семейства, называемого демигиперкубами .
5-куб можно рассматривать как тессерактическую соту 3-го порядка на 4-сфере . Это связано с евклидовой 4-пространственной (порядка 4) тессерактической сотой и паракомпактной гиперболической сотой тессерактической соты 5-го порядка .
В качестве конфигурации
[ редактировать ]Эта матрица конфигурации представляет собой 5-куб. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам и 4-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем 5-кубе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. [1] [2]
Декартовы координаты
[ редактировать ]Декартовы координаты вершин 5-куба с центром в начале координат и длиной ребра 2 равны
- (±1,±1,±1,±1,±1),
в то время как внутренняя часть этого 5-куба состоит из всех точек ( x 0 , x 1 , x 2 , x 3 , x 4 ) с -1 < x i < 1 для всех i .
Изображения
[ редактировать ]Проекции на плоскость n -куба Кокстера в группах B k Кокстера проецируются в графы k-кубов со степенью двух вершин, перекрывающихся в проективных графах.
| Самолет Коксетера | Б 5 | Б 4 / Д 5 | Б 3 / Д 4 / А 2 |
|---|---|---|---|
| График |  |  | 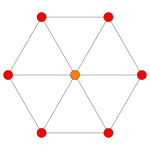 |
| Двугранная симметрия | [10] | [8] | [6] |
| Самолет Коксетера | Другой | BБ2 | AА3 |
| График |  | 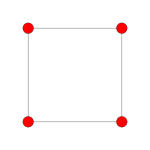 | 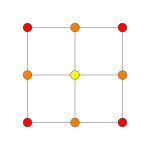 |
| Двугранная симметрия | [2] | [4] | [4] |
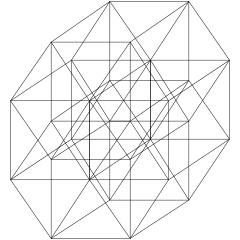 Направление перекоса каркаса |  B5 Коксетера Самолет |
 Граф вершин-ребер. |
 Перспективная проекция 3D в 2D, стереографическая проекция с 4D на 3D, диаграмма Шлегеля с 5D на 4D. |
 4D-сеть 5-куба, перспектива, проецируемая в 3D. |
Проекция
[ редактировать ]Пятимерный куб можно спроецировать в трех измерениях с помощью оболочки ромбического икосаэдра . Всего имеется 22 внешние вершины и 10 внутренних вершин. Десять внутренних вершин имеют выпуклую оболочку пятиугольной антипризмы . 80 ребер образуют 40 внешних и 40 внутренних ребер. 40 кубов образуют золотые ромбоэдры , которые можно использовать для разрезания ромбического икосаэдра. Векторы проекции: u = {1, φ, 0, -1, φ}, v = {φ, 0, 1, φ, 0}, w = {0, 1, φ, 0, -1}, где φ это золотое сечение , .
| ромбический икосаэдр | 5-куб | |
|---|---|---|
| Перспектива | ортогональный | |
 |  |  |
Также возможно проецировать пентеракты в трехмерное пространство, аналогично проецированию куба в двухмерное пространство.
 Трехмерная перспективная проекция пентеракта, подвергающегося простому вращению W1-W2. вокруг ортогональной плоскости Трехмерная перспективная проекция пентеракта, подвергающегося простому вращению W1-W2. вокруг ортогональной плоскости |  Трехмерная перспективная проекция пентеракта, совершающего двойной поворот X-W1 и Z-W2. вокруг ортогональных плоскостей Трехмерная перспективная проекция пентеракта, совершающего двойной поворот X-W1 и Z-W2. вокруг ортогональных плоскостей |
Симметрия
[ редактировать ]имеет 5-куб симметрию группы Кокстера B 5 , абстрактную структуру. , порядка 3840, содержащий 25 гиперплоскостей отражения. Символ Шлефли для 5-куба {4,3,3,3} соответствует симметрии обозначений Коксетера [4,3,3,3].
Призмы
[ редактировать ]Все гиперкубы имеют формы более низкой симметрии, построенные в виде призм. 5-куб имеет 7 призматических форм из низшего 5- ортотопа , { } 5 и вверх, поскольку ортогональные ребра должны иметь одинаковую длину. Вершины призмы равны произведению вершин элементов. Ребра призмы можно разделить на количество ребер в элементе, умноженное на количество вершин во всех остальных элементах.
| Описание | Символ Шлефли | Диаграмма Кокстера-Динкина | Вершины | Края | Обозначение Кокстера Симметрия | Заказ |
|---|---|---|---|---|---|---|
| 5-куб | {4,3,3,3} | 32 | 80 | [4,3,3,3] | 3840 | |
| тессерактическая призма | {4,3,3}×{ } | 16×2 = 32 | 64 + 16 = 80 | [4,3,3,2] | 768 | |
| куб - квадратная дуопризма | {4,3}×{4} | 8×4 = 32 | 48 + 32 = 80 | [4,3,2,4] | 384 | |
| кубо- прямоугольная дуопризма | {4,3}×{ } 2 | 8×2 2 = 32 | 48 + 2×16 = 80 | [4,3,2,2] | 192 | |
| квадрат-квадрат дуопризма призма | {4} 2 ×{ } | 4 2 ×2 = 32 | 2×32 + 16 = 80 | [4,2,4,2] | 128 | |
| квадратно -прямоугольного параллелепипеда дуопризма | {4}×{ } 3 | 4×2 3 = 32 | 32 + 3×16 = 80 | [4,2,2,2] | 64 | |
| 5- ортотоп | { } 5 | 2 5 = 32 | 5×16 = 80 | [2,2,2,2] | 32 |
Связанные многогранники
[ редактировать ]— 5-куб пятый в ряду гиперкубов :
 |  |  |  |  |  |  |  |  |  |
| Отрезок линии | Квадрат | Куб | 4-кубовый | 5-куб | 6-куб. | 7-куб | 8-кубовый | 9-куб | 10-кубовый |
Правильный косой многогранник {4,5| 4} может быть реализован внутри 5-куба с его 32 вершинами, 80 ребрами и 40 квадратными гранями, а остальные 40 квадратных граней 5-куба становятся квадратными отверстиями .
Этот многогранник является одним из 31 однородных 5-многогранников, порожденных из правильного 5-куба или 5-ортоплекса .
| Многогранники B5 |
|---|
Ссылки
[ редактировать ]- ХСМ Коксетер :
- Коксетер, Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 , с. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
- Клитцинг, Ричард. «5D однородные многогранники (политеры) o3o3o3o4x — пент.» .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперкуб» . Математический мир .
- Ольшевский, Георгий. «Измерить многогранник» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Многомерный глоссарий: гиперкуб Гаррета Джонса
- Мальцев, Ник Э. https://www.asymptotos.com/wp-content/uploads/2023/07/Cube_5.html

































