Цикл Карно

Внешние видео
Внешние видео
	Цикл Карно из «Механической вселенной»

Цикл Карно — это идеальный термодинамический цикл, предложенный французским физиком Сади Карно в 1824 году и расширенный другими в 1830-х и 1840-х годах. По теореме Карно она обеспечивает верхний предел эффективности любого классического термодинамического двигателя при преобразовании тепла в работу или, наоборот, эффективности холодильной системы при создании разницы температур за счет приложения работы к системе.

В цикле Карно система или двигатель передает энергию в виде тепла между двумя тепловыми резервуарами при температурах $T_{H}$ и $T_{C}$ (называемые горячим и холодным резервуарами соответственно), и часть этой переданной энергии преобразуется в работу, совершаемую системой. Цикл обратим , и энтропия сохраняется , просто переносится между термальными резервуарами и системой без выигрыша или потери. Когда в системе совершается работа, тепло перемещается из холодного резервуара в горячий ( тепловой насос или холодильное оборудование ). Когда тепло перемещается из горячего резервуара в холодный, система совершает работу в окружающей среде. Работа $W$ выполняемый системой или двигателем в окружающую среду за цикл Карно, зависит от температуры тепловых резервуаров и энтропии, передаваемой из горячего резервуара в систему. $\Delta S$ за цикл, например $W=(T_{H}-T_{C})\Delta S=(T_{H}-T_{C}){\frac {Q_{H}}{T_{H}}}$ , где $Q_{H}$ — тепло, передаваемое от горячего резервуара к системе за цикл.

Этапы

Цикл Карно как идеализированный термодинамический цикл, выполняемый тепловой машиной Карно , состоящий из следующих этапов:

Изотермическое расширение. Тепло (как энергия) передается обратимо от горячего резервуара с постоянной температурой T _H к газу с температурой бесконечно меньшей, чем T _H . (Бесконечно малая разница температур позволяет теплу передаваться в газ без существенного изменения температуры газа. Это называется изотермическим добавлением или поглощением тепла .) На этом этапе (от 1 до 2 на рисунке 1 , от A до B на рисунке 2 ) газ находится в термическом контакте с резервуаром с горячей температурой и термически изолирован от резервуара с холодной температурой. Газу позволяют расширяться, совершая работу над окружающей средой, толкая поршень вверх (рисунок первой стадии справа). Хотя давление падает от точек 1 до 2 (рисунок 1), температура газа не меняется в ходе процесса, поскольку тепло, передаваемое от горячего резервуара к газу, именно используется для совершения газом работы над окружающей средой. Внутренняя энергия газа не изменяется, как и температура газа, если это идеальный газ. Нагревать Q _H > 0 поглощается из горячего резервуара, что приводит к увеличению энтропии $S$ газа на количество $\Delta S_{H}=Q_{H}/T_{H}$ .
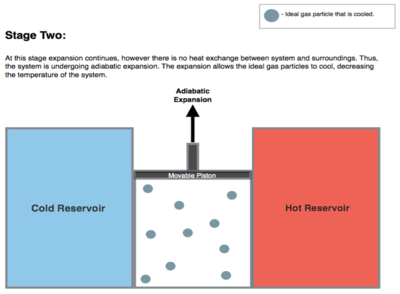
Изэнтропическое ( обратимое адиабатическое ) расширение газа (изоэнтропическая работа). На этом этапе (2–3 на рисунке 1 , B–C на рисунке 2 ) газ в двигателе теплоизолируется как от горячего, так и от холодного резервуаров, поэтому они не получают и не теряют тепло. Это адиабатический процесс . Газ продолжает расширяться при уменьшении своего давления, совершая работу над окружающей средой (поднимая поршень; рисунок второго этапа справа) и теряя количество внутренней энергии, равное совершенной работе. Потеря внутренней энергии приводит к охлаждению газа. которая бесконечно выше температуры холодного резервуара TC _. На этом этапе он охлаждается до температуры , Энтропия остается неизменной, поскольку тепло Q не передается ( Q = 0) между системой (газом) и ее окружением. Это изэнтропический процесс .
Изотермическое сжатие. Тепло передается обратимо в низкотемпературный резервуар при постоянной температуре T _C (изотермический отвод тепла). На этом этапе (3-4 на рисунке 1 , C-D на рисунке 2 ) газ в двигателе находится в термическом контакте с холодным резервуаром при температуре T _C и термически изолирован от горячего резервуара. Температура газа бесконечно выше T _C , чтобы обеспечить передачу тепла от газа к холодному резервуару. Изменения температуры нет, это изотермический процесс . Окружающая среда воздействует на газ, толкая поршень вниз (рисунок третьего этапа справа). Количество энергии, полученной газом в результате этой работы, точно передается в виде тепловой энергии Q _C < 0 (отрицательной, если она уходит из системы, согласно универсальному соглашению в термодинамике ) в холодный резервуар, поэтому энтропия системы уменьшается на величину количество $\Delta S_{C}=Q_{C}/T_{C}$ . ^[1] $\Delta S_{C}<0$ поскольку изотермическое сжатие уменьшает кратность газа.
Изэнтропическое сжатие. (от 4 до 1 на рисунке 1 , от D до A на рисунке 2 ). И снова газ в двигателе теплоизолирован от горячего и холодного резервуаров, предполагается, что двигатель работает без трения, а процесс достаточно медленный и, следовательно, обратимый. На этом этапе окружающая среда воздействует на газ, толкая поршень дальше вниз (рисунок четвертого этапа справа), увеличивая его внутреннюю энергию, сжимая его и заставляя его температуру снова подняться до температуры, бесконечно меньшей, чем T _H, исключительно за счет к работе добавляется система, но энтропия остается неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.

В данном случае, поскольку это обратимый термодинамический цикл (нет чистых изменений в системе и ее окружении за цикл) ^[2]^[1] $\Delta S_{H}+\Delta S_{C}=\Delta S_{\text{cycle}}=0,$ или, ${\frac {Q_{H}}{T_{H}}}=-{\frac {Q_{C}}{T_{C}}}.$

Это верно, как $Q_{C}$ и $T_{C}$ оба меньше по величине и фактически находятся в том же соотношении, что и $Q_{H}/T_{H}$ .

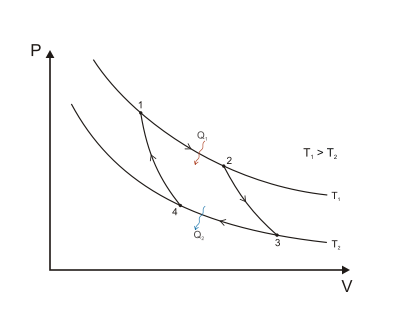
График давление-объем

Когда цикл Карно отображается на диаграмме давление-объем ( рис. 1 ), изотермические стадии следуют линиям изотерм рабочего тела, адиабатические стадии перемещаются между изотермами, а область, ограниченная полным путем цикла, представляет собой полную работу, которую можно сделать за один цикл. От точки 1 до 2 и от точки 3 до 4 температура постоянна (изотермический процесс). Теплопередача от точки 4 к 1 и от точки 2 к 3 равна нулю (адиабатический процесс).

Свойства и значение

Диаграмма температура–энтропия

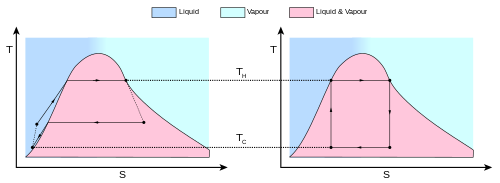
Поведение двигателя Карно или холодильника лучше всего понять с помощью диаграммы температура-энтропия ( диаграмма T – S ), в которой термодинамическое состояние задается точкой на графике с энтропией ( S ) в качестве горизонтальной оси и температурой ( T ) в качестве вертикальной оси ( рис. 2 ). Для простой закрытой системы (анализ контрольной массы) любая точка на графике представляет определенное состояние системы. Термодинамический процесс изображается кривой, соединяющей начальное состояние (А) и конечное состояние (Б). Площадь под кривой равна:

Q=\int _{A}^{B}dQ=\int _{A}^{B}T\,dS

( 1 )

это количество тепла, переданное в процессе. Если процесс приводит систему к большей энтропии, площадь под кривой представляет собой количество тепла, поглощенное системой в этом процессе; в противном случае это количество тепла, отводимого из системы или покидающего ее. Для любого циклического процесса существует верхняя часть цикла и нижняя часть. На диаграммах T – S для цикла по часовой стрелке площадь под верхней частью будет представлять собой энергию, поглощенную системой во время цикла, а площадь под нижней частью будет представлять собой энергию, удаленную из системы во время цикла. Площадь внутри цикла тогда представляет собой разницу между ними (поглощенную чистую тепловую энергию), но поскольку внутренняя энергия системы должна вернуться к своему первоначальному значению, эта разница должна быть количеством работы, совершаемой системой за цикл. . Ссылаясь на рисунок 1 , математически для обратимого процесса мы можем записать объем работы, выполняемой в течение циклического процесса, как:

W=\oint PdV=\oint (dQ-dU)=\oint (TdS-dU)=\oint TdS-\oint dU=\oint TdS

( 2 )

Поскольку dU является точным дифференциалом , его интеграл по любому замкнутому контуру равен нулю, и отсюда следует, что площадь внутри контура на диаграмме T – S (а) равна полной работе, выполняемой системой над окружением, если контур проходится по часовой стрелке, и (b) равна общей работе, совершаемой над системой окружающей средой при прохождении петли против часовой стрелки.

Цикл Карно

Вычисление приведенного выше интеграла особенно просто для цикла Карно. Количество энергии, переданной в виде работы, равно

$W=\oint PdV=\oint TdS=(T_{H}-T_{C})(S_{B}-S_{A})$

Общее количество тепла, переданное от горячего резервуара в систему (при изотермическом расширении), будет равно $Q_{H}=T_{H}(S_{B}-S_{A})=T_{H}\Delta S_{H}$ а общее количество тепла, передаваемое от системы к холодному резервуару (при изотермическом сжатии), будет $Q_{C}=T_{C}(S_{A}-S_{B})=T_{C}\Delta S_{C}<0$

Из-за энергосбережения чистая передаваемая теплота, $Q$ , равен произведенной работе ^[1] $W=Q=Q_{H}-Q_{C}$

Эффективность $\eta$ определяется как:

\eta ={\frac {W}{Q_{H}}}={\frac {Q_{H}-Q_{C}}{Q_{H}}}=1-{\frac {T_{C}}{T_{H}}}

( 3 )

где

$W$ — работа, совершенная системой (энергия, выходящая из системы в виде работы),
$Q_{C}$ < 0 – тепло, отбираемое из системы (тепловая энергия, покидающая систему),
$Q_{H}$ > 0 – подведенное в систему тепло (тепловая энергия, поступающая в систему),
$T_{C}$ - абсолютная температура холодного резервуара, а
$T_{H}$ – абсолютная температура горячего резервуара.
$S_{B}$ максимальная энтропия системы
$S_{A}$ - минимальная энтропия системы

Выражение с температурой $\eta =1-{\frac {T_{C}}{T_{H}}}$ может быть получена из приведенных выше выражений с энтропией: $Q_{H}=T_{H}(S_{B}-S_{A})=T_{H}\Delta S_{H}$ и $Q_{C}=T_{C}(S_{A}-S_{B})=T_{C}\Delta S_{C}<0$ . С $\Delta S_{C}=S_{A}-S_{B}=-\Delta S_{H}$ , в конечном выражении для $\eta$ .

Это определение эффективности работы теплового двигателя Карно как доля работы, совершаемой системой, по отношению к тепловой энергии, полученной системой из горячего резервуара за цикл. Эта тепловая энергия является инициатором цикла.

Обратный цикл Карно

Описанный цикл тепловой машины Карно является полностью обратимым циклом. То есть все процессы, из которых он состоит, можно обратить вспять, и в этом случае он становится тепловым насосом Карно и холодильным циклом . На этот раз цикл остается точно таким же, за исключением того, что направления любых тепловых и рабочих взаимодействий меняются местами. Тепло поглощается из низкотемпературного резервуара, тепло отводится в высокотемпературный резервуар, и для всего этого требуется затрата работы. диаграмма P – V- обратного цикла Карно такая же, как и для цикла тепловой машины Карно, за исключением того, что направления процессов обратные. ^[3]

Теорема Карно

Из приведенной выше диаграммы видно, что для любого цикла, работающего между температурами $T_{H}$ и $T_{C}$ , ни один из них не может превысить эффективность цикла Карно.

Теорема Карно является формальным утверждением этого факта: ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между теми же самыми резервуарами. Таким образом, уравнение 3 дает максимально возможный КПД для любого двигателя при соответствующих температурах. Следствие теоремы Карно гласит: Все обратимые двигатели, работающие с одними и теми же тепловыми резервуарами, одинаково эффективны. Перестановка правой части уравнения дает более понятную форму уравнения, а именно: теоретический максимальный КПД теплового двигателя равен разнице температур между горячим и холодным резервуаром, деленной на абсолютную температуру горячего резервуара. . Глядя на эту формулу, становится очевидным интересный факт: понижение температуры холодного резервуара окажет большее влияние на максимальный КПД теплового двигателя, чем повышение температуры горячего резервуара на ту же величину. В реальном мире этого может быть трудно достичь, поскольку холодный резервуар часто имеет существующую температуру окружающей среды.

Другими словами, максимальная эффективность достигается тогда и только тогда, когда энтропия не меняется за цикл. Изменение энтропии за цикл происходит, например, при наличии трения, приводящего к рассеиванию работы в тепло. В этом случае цикл необратим, и теорема Клаузиуса становится неравенством, а не равенством. В противном случае, поскольку энтропия является функцией состояния , необходимый сброс тепла в окружающую среду для избавления от избыточной энтропии приводит к (минимальному) снижению эффективности. Итак, уравнение 3 дает КПД любого обратимого теплового двигателя .

В мезоскопических тепловых двигателях работа за цикл работы обычно колеблется из-за теплового шума. Если цикл осуществляется квазистатически, флуктуации исчезают даже на мезомасштабе. ^[4] Однако если цикл выполняется быстрее времени релаксации рабочего тела, колебания работы неизбежны. Тем не менее, когда подсчитываются работа и тепловые колебания, точное равенство связывает среднее экспоненциальное значение работы, выполняемой любой тепловой машиной, с передачей тепла от более горячей тепловой ванны. ^[5]

КПД реальных тепловых двигателей

Карно понял, что на самом деле невозможно построить термодинамически обратимый двигатель. Итак, реальные тепловые двигатели даже менее эффективны, чем указано уравнением 3 . Кроме того, реальные двигатели, работающие по циклу Карно (изотермическое расширение/изоэнтропическое расширение/изотермическое сжатие/изоэнтропическое сжатие), встречаются редко. Тем не менее, уравнение 3 чрезвычайно полезно для определения максимальной эффективности, которую можно ожидать для данного набора тепловых резервуаров.

Хотя цикл Карно является идеализацией, уравнение 3 как выражение эффективности Карно все еще полезно. Рассмотрим средние температуры, $\langle T_{H}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{in}}}TdS$ $\langle T_{C}\rangle ={\frac {1}{\Delta S}}\int _{Q_{\text{out}}}TdS$ при котором первый интеграл относится к той части цикла, где тепло поступает в систему, а второй интеграл относится к той части цикла, когда тепло выходит из системы. Затем замените TH _на и TC _{соответственно, чтобы} уравнении 3 ⟨ TH _в ⟩ и ⟨ TC _⟩ оценить эффективность теплового двигателя.

цикла Карно или его эквивалента среднее значение ⟨ T _H самой высокой доступной температуре, а именно , _TH и ⟨ TC _Для ⟩ самой низкой, а именно TC _{⟩ будет равно} . менее эффективных термодинамических циклов ⟨ T _H ⟩ будет ниже, чем , _{Для других} а ⟨ TC _TC ⟩ будет выше, чем _TH . Это может помочь проиллюстрировать, например, почему промежуточный перегреватель или регенератор могут улучшить тепловой КПД паровых электростанций и почему тепловой КПД электростанций с комбинированным циклом (которые включают в себя газовые турбины, работающие при еще более высоких температурах) превышает тепловой КПД традиционных паровых электростанций. растения. Первый прототип дизельного двигателя был основан на принципах цикла Карно.

Как макроскопическая конструкция

, Тепловая машина Карно в конечном счете, представляет собой теоретическую конструкцию, основанную на идеализированной термодинамической системе . На практическом уровне человеческого масштаба цикл Карно оказался ценной моделью, например, для продвижения разработки дизельного двигателя . Однако в макроскопическом масштабе ограничения, налагаемые предположениями модели, доказывают ее непрактичность и, в конечном итоге, неспособность выполнять какую-либо работу . ^[6] Таким образом, согласно теореме Карно , двигатель Карно можно рассматривать как теоретический предел тепловых двигателей макроскопического масштаба, а не как любое практическое устройство, которое когда-либо могло быть построено. ^[7]

См. также

Ссылки

Примечания

^ Jump up to: ^а ^б ^с Планк, М. (1945). «уравнения 39, 40 и 65 в разделах §90 и §137». Трактат по термодинамике . Дуврские публикации. стр. 75, 135.
^ Ферми, Э. (1956). «уравнение 64». Термодинамика (PDF) . Дуврские публикации. п. 48.
^ Ченгель, Юнус А. и Майкл А. Болес. Термодинамика: инженерный подход . 7-е изд. Нью-Йорк: МакГроу-Хилл, 2011. с. 299. Печать.
^ Голубец Виктор и Рябов Артем (2018). «Велоспорт укрощает колебания мощности, приближаясь к оптимальной эффективности». Физ. Преподобный Летт . 121 (12): 120601. arXiv : 1805.00848 . Бибкод : 2018PhRvL.121l0601H . doi : 10.1103/PhysRevLett.121.120601 . ПМИД 30296120 . S2CID 52943273 .
^ Н.А. Синицын (2011). «Флуктуационное соотношение для тепловых двигателей». Дж. Физ. А: Математика. Теор . 44 (40): 405001. arXiv : 1111.7014 . Бибкод : 2011JPhA...44N5001S . дои : 10.1088/1751-8113/44/40/405001 . S2CID 119261929 .
^ Лю, Ханг; Мэн, Синь-Хе (18 августа 2017 г.). «Влияние темной энергии на эффективность заряженных черных дыр AdS как тепловых двигателей» . Европейский физический журнал C . 77 (8): 556. arXiv : 1704.04363 . doi : 10.1140/epjc/s10052-017-5134-9 . ISSN 1434-6052 . ... поскольку тепловой двигатель Карно, установка верхней границы эффективности теплового двигателя является идеальным обратимым двигателем, один цикл которого должен выполняться за бесконечное время, что непрактично, и поэтому двигатель Карно имеет нулевую мощность.
^ Бененти, Джулиано; Казати, Джулио; Ван, Цзяо (2020). «Мощность, эффективность и колебания стационарных тепловых двигателей» (PDF) . Физический обзор E . 102 (4). Однако колебания [температуры пласта] делают такие двигатели непрактичными.

Источники

Карно, Сади, Размышления о движущей силе огня
Юинг, Дж. А. (1910) Паровая машина и другие двигатели, издание 3, стр. 62, через Интернет-архив.
Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (1963). Фейнмановские лекции по физике . Издательство Аддисон-Уэсли. стр. Глава 44 . ISBN 978-0-201-02116-5 .
Холлидей, Дэвид; Резник, Роберт (1978). Физика (3-е изд.). Джон Уайли и сыновья. стр. 541–548 . ISBN 978-0-471-02456-9 .
Киттель, Чарльз ; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания WH Freeman. ISBN 978-0-7167-1088-2 .
Костич, М (2011). «Возвращение ко второму закону деградации энергии и генерации энтропии: от гениальных рассуждений Сади Карно к целостному обобщению». Конференция АИП. Проц . Материалы конференции AIP. 1411 (1): 327–350. Бибкод : 2011AIPC.1411..327K . CiteSeerX 10.1.1.405.1945 . дои : 10.1063/1.3665247 . Американский институт физики, 2011. ISBN 978-0-7354-0985-9 . Аннотация: [1] . Полная статья (24 страницы [2] ), также по адресу [3] .

Внешние ссылки

Статья по гиперфизике о цикле Карно.
Цикл Карно Блиндера SM на идеальном газе на базе Wolfram Mathematica

[PlanckBook-1] Jump up to: ^а ^б ^с Планк, М. (1945). «уравнения 39, 40 и 65 в разделах §90 и §137». Трактат по термодинамике . Дуврские публикации. стр. 75, 135.

[FermiBook-2] Ферми, Э. (1956). «уравнение 64». Термодинамика (PDF) . Дуврские публикации. п. 48.

[3] Ченгель, Юнус А. и Майкл А. Болес. Термодинамика: инженерный подход . 7-е изд. Нью-Йорк: МакГроу-Хилл, 2011. с. 299. Печать.

[4] Голубец Виктор и Рябов Артем (2018). «Велоспорт укрощает колебания мощности, приближаясь к оптимальной эффективности». Физ. Преподобный Летт . 121 (12): 120601. arXiv : 1805.00848 . Бибкод : 2018PhRvL.121l0601H . doi : 10.1103/PhysRevLett.121.120601 . ПМИД 30296120 . S2CID 52943273 .

[5] Н.А. Синицын (2011). «Флуктуационное соотношение для тепловых двигателей». Дж. Физ. А: Математика. Теор . 44 (40): 405001. arXiv : 1111.7014 . Бибкод : 2011JPhA...44N5001S . дои : 10.1088/1751-8113/44/40/405001 . S2CID 119261929 .

[hang-6] Лю, Ханг; Мэн, Синь-Хе (18 августа 2017 г.). «Влияние темной энергии на эффективность заряженных черных дыр AdS как тепловых двигателей» . Европейский физический журнал C . 77 (8): 556. arXiv : 1704.04363 . doi : 10.1140/epjc/s10052-017-5134-9 . ISSN 1434-6052 . ... поскольку тепловой двигатель Карно, установка верхней границы эффективности теплового двигателя является идеальным обратимым двигателем, один цикл которого должен выполняться за бесконечное время, что непрактично, и поэтому двигатель Карно имеет нулевую мощность.

[7] Бененти, Джулиано; Казати, Джулио; Ван, Цзяо (2020). «Мощность, эффективность и колебания стационарных тепловых двигателей» (PDF) . Физический обзор E . 102 (4). Однако колебания [температуры пласта] делают такие двигатели непрактичными.

[1]

[2]

[3]

[4]

[5]

[6]

[7]