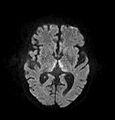
Диффузионная МРТ

Диффузионная МРТ
Карта цветов DTI
МеШ	Д038524

Диффузионно-взвешенная магнитно-резонансная томография ( ДВИ или ДВ-МРТ ) — это использование определенных последовательностей МРТ , а также программного обеспечения, которое генерирует изображения на основе полученных данных и использует диффузию молекул воды для создания контраста на МР-изображениях. Он позволяет картировать процесс диффузии молекул, главным образом воды, в тканях биологических in vivo и неинвазивно. Молекулярная диффузия в тканях не случайна, а отражает взаимодействие со многими препятствиями, такими как макромолекулы , волокна и мембраны . Таким образом, закономерности диффузии молекул воды могут раскрыть микроскопические детали архитектуры тканей, как в нормальном, так и в болезненном состоянии. Особый вид DWI, диффузионно-тензорная визуализация ( DTI ), широко используется для картографии белого вещества трактографии головного мозга.

Введение

В диффузионно-взвешенной визуализации (DWI) интенсивность каждого элемента изображения ( вокселя ) отражает наилучшую оценку скорости диффузии воды в этом месте. Поскольку подвижность воды обусловлена ​​тепловым перемешиванием и сильно зависит от ее клеточной среды, гипотеза, лежащая в основе DWI, заключается в том, что результаты могут указывать на (ранние) патологические изменения. Например, DWI более чувствителен к ранним изменениям после инсульта, чем более традиционные измерения МРТ, такие как скорость релаксации T1 или T2 . Вариант диффузионно-взвешенной визуализации, визуализация диффузионного спектра (DSI), использовался при получении наборов данных Connectome; DSI - это вариант диффузионно-взвешенной визуализации, который чувствителен к внутривоксельным неоднородностям в направлениях диффузии, вызванным пересечением волоконных трактов, и, таким образом, позволяет более точно отображать аксональные траектории, чем другие подходы к диффузионной визуализации.

Диффузионно-взвешенные изображения очень полезны для диагностики сосудистых инсультов головного мозга. Его также все чаще используют при определении стадии немелкоклеточного рака легких , где он является серьезным кандидатом на замену позитронно-эмиссионной томографии в качестве «золотого стандарта» для этого типа заболевания. Разрабатывается диффузионно-тензорная томография для изучения заболеваний белого вещества головного мозга, а также других тканей организма (см. ниже). ДВИ наиболее применим, когда в интересующей ткани преобладает изотропное движение воды, например, в сером веществе в коре головного мозга и основных ядрах мозга или в организме, где скорость диффузии кажется одинаковой при измерении вдоль любой оси. Однако ДВИ также остается чувствительным к релаксации Т1 и Т2. Чтобы связать эффекты диффузии и релаксации с контрастностью изображения, можно получить количественные изображения коэффициента диффузии или, точнее, кажущегося коэффициента диффузии (ADC). Концепция ADC была введена с учетом того факта, что процесс диффузии в биологических тканях сложен и отражает несколько различных механизмов.

Диффузионно-тензорная визуализация (DTI) важна, когда ткань, такая как нервные аксоны головного белого вещества мозга или мышечные волокна сердца, имеет внутреннюю волокнистую структуру, аналогичную анизотропии некоторых кристаллов. Тогда вода будет диффундировать быстрее в направлении, соответствующем внутренней структуре (осевая диффузия), и медленнее, когда она движется перпендикулярно предпочтительному направлению (радиальная диффузия). Это также означает, что измеренная скорость диффузии будет различаться в зависимости от направления, с которого смотрит наблюдатель.

Визуализация базисного спектра диффузии (DBSI) дополнительно разделяет сигналы DTI на дискретные тензоры анизотропной диффузии и спектр тензоров изотропной диффузии, чтобы лучше дифференцировать субвоксельные клеточные структуры. Например, тензоры анизотропной диффузии коррелируют с аксональными волокнами, в то время как тензоры с низкой изотропной диффузией коррелируют с клетками, а тензоры с высокой изотропной диффузией коррелируют с более крупными структурами (такими как просвет или желудочки мозга). Было показано, что DBSI дифференцирует некоторые типы опухолей головного мозга и рассеянный склероз с более высокой специфичностью и чувствительностью, чем обычный DTI. DBSI также оказался полезен при определении свойств микроструктуры мозга.

Традиционно при диффузионно-взвешенной визуализации (ДВИ) применяются три направления градиента, достаточные для оценки следа тензора диффузии или «средней диффузионной способности», предполагаемой меры отека . Клинически, взвешенные изображения оказались очень полезными для диагностики сосудистых инсультов в головном мозге путем раннего выявления (в течение нескольких минут) гипоксического отека.

Более расширенные сканирования DTI извлекают информацию о направлении нервного тракта из данных с использованием трехмерных или многомерных векторных алгоритмов, основанных на шести или более направлениях градиента, достаточных для вычисления тензора диффузии . Модель тензора диффузии представляет собой довольно простую модель процесса диффузии, предполагающую однородность и линейность диффузии внутри каждого вокселя изображения. Из тензора диффузии меры диффузионной анизотропии, такие как дробная анизотропия можно вычислить (FA). Более того, основное направление тензора диффузии можно использовать для вывода о связности белого вещества мозга (т. е. трактографии ; попытка увидеть, какая часть мозга связана с какой другой частью).

Недавно были предложены более совершенные модели процесса диффузии, целью которых является преодоление недостатков модели тензора диффузии. Среди прочего, к ним относятся изображения в q-пространстве. и обобщенная диффузионно-тензорная визуализация.

Механизм

Диффузионная визуализация - это метод МРТ , который создает магнитно-резонансные изображения in vivo биологических тканей, сенсибилизированных локальными характеристиками молекулярной диффузии, обычно воды (но другие фрагменты также можно исследовать с помощью подходов МР-спектроскопии). МРТ можно сделать чувствительным к движению молекул. Регулярное получение МРТ использует поведение протонов в воде для создания контраста между клинически значимыми особенностями конкретного субъекта. Универсальная природа МРТ обусловлена ​​способностью создавать контраст, связанный со структурой тканей на микроскопическом уровне. В типичном $T_{1}$На взвешенном изображении молекулы воды в образце возбуждаются под действием сильного магнитного поля. Это приводит к одновременной прецессии многих протонов в молекулах воды, создавая сигналы при МРТ. В $T_{2}$На взвешенных изображениях контраст создается путем измерения потери когерентности или синхронности между протонами воды. Когда вода находится в среде, где она может свободно падать, расслабление обычно занимает больше времени. В определенных клинических ситуациях это может создать контраст между областью патологии и окружающей здоровой тканью.

Чтобы повысить чувствительность МРТ-изображений к диффузии, напряженность магнитного поля (B1) изменяется линейно с помощью градиента импульсного поля. Поскольку прецессия пропорциональна силе магнита, протоны начинают прецессировать с разной скоростью, что приводит к дисперсии фазы и потере сигнала. Другой градиентный импульс подается той же величины, но с противоположным направлением, чтобы перефокусировать или перефазировать спины. Перефокусировка не будет идеальной для протонов, которые переместились за промежуток времени между импульсами, и сигнал, измеряемый аппаратом МРТ, уменьшится. Этот метод «импульса градиента поля» был первоначально разработан для ЯМР Стейскалом и Таннером. который вывел уменьшение сигнала из-за применения импульсного градиента, связанное с величиной происходящей диффузии, посредством следующего уравнения:

${\frac {S(TE)}{S_{0}}}=\exp \left[-\gamma ^{2}G^{2}\delta ^{2}\left(\Delta -{\frac {\delta }{3}}\right)D\right]$

где $S_{0}$ — интенсивность сигнала без учета диффузионного взвешивания, $S$ — сигнал с градиентом, $\gamma$ гиромагнитное отношение , $G$ – сила градиентного импульса, $\delta$ - длительность импульса, $\Delta$ это время между двумя импульсами, и, наконец, $D$ - коэффициент диффузии.

Чтобы локализовать это затухание сигнала и получить изображения диффузии, необходимо объединить импульсные импульсы градиента магнитного поля, используемые для МРТ (нацеленные на локализацию сигнала, но эти градиентные импульсы слишком слабы, чтобы вызвать ослабление, связанное с диффузией) с дополнительными градиентные импульсы зондирования движения в соответствии с методом Стейскала и Таннера. Эта комбинация нетривиальна, поскольку между всеми градиентными импульсами возникают перекрестные члены. Тогда уравнение, установленное Стейскалом и Таннером, становится неточным, и затухание сигнала необходимо рассчитывать либо аналитически, либо численно, интегрируя все градиентные импульсы, присутствующие в последовательности МРТ, и их взаимодействия. Результат быстро становится очень сложным, учитывая множество импульсов, присутствующих в последовательности МРТ, и в качестве упрощения Ле Биан предложил собрать все градиентные члены в «факторе b» (который зависит только от параметров сбора данных), чтобы затухание сигнала просто становится:

${\frac {S(TE)}{S_{0}}}=\exp(-b\cdot ADC)$

Кроме того, коэффициент диффузии $D$, заменяется кажущимся коэффициентом диффузии, $ADC$, чтобы указать, что процесс диффузии не является свободным в тканях, но затруднен и модулируется многими механизмами (ограничение в закрытых пространствах, извилистость вокруг препятствий и т. д.) и что другие источники внутривоксельного некогерентного движения (IVIM), такие как кровоток в небольших сосуды или спинномозговая жидкость в желудочках также способствуют ослаблению сигнала.В конце концов, изображения «взвешиваются» в процессе диффузии: в этих диффузионно-взвешенных изображениях (DWI) сигнал тем сильнее ослабляется, чем быстрее диффузия и чем больше коэффициент b. Однако эти диффузионно-взвешенные изображения по-прежнему чувствительны к контрасту релаксации Т1 и Т2, что иногда может сбивать с толку. Можно рассчитать «чистые» карты диффузии (или, точнее, карты АЦП, где АЦП является единственным источником контраста), собрав изображения как минимум с двумя разными значениями: $b_{1}$ и $b_{2}$, фактора b согласно:

$\mathrm {ADC} (x,y,z)=\ln[S_{2}(x,y,z)/S_{1}(x,y,z)]/(b_{1}-b_{2})$

Хотя эта концепция ADC оказалась чрезвычайно успешной, особенно для клинических применений, в последнее время она была поставлена ​​под сомнение, поскольку были представлены новые, более полные модели диффузии в биологических тканях. Эти модели были необходимы, поскольку диффузия в тканях не является свободной. В этом состоянии АЦП, по-видимому, зависит от выбора значений b (по-видимому, АЦП уменьшается при использовании больших значений b), поскольку график ln(S/So) не является линейным с коэффициентом b, как и ожидалось из приведенные выше уравнения. Это отклонение от режима свободной диффузии и делает диффузионную МРТ такой успешной, поскольку ADC очень чувствителен к изменениям микроструктуры ткани. С другой стороны, моделирование диффузии в тканях становится очень сложным. Среди наиболее популярных моделей – биэкспоненциальная модель, предполагающая наличие двух водоемов с медленным или промежуточным обменом. и модель кумулянтного расширения (также называемая куртозисом), что не обязательно требует наличия 2-х пулов.

Диффузионная модель

Учитывая концентрацию $\rho$ и поток $J$ дает Первый закон Фика связь между потоком и градиентом концентрации :

$J(x,t)=-D\nabla \rho (x,t)$

где D – коэффициент диффузии . Тогда, учитывая сохранение массы, уравнение неразрывности связывает производную концентрации по времени с дивергенцией потока:

${\frac {\partial \rho (x,t)}{\partial t}}=-\nabla \cdot J(x,t)$

Сложив их вместе, мы получаем уравнение диффузии :

${\frac {\partial \rho (x,t)}{\partial t}}=D\nabla ^{2}\rho (x,t).$

Динамика намагничивания

В отсутствие диффузии изменение ядерной намагниченности с течением времени определяется классическим уравнением Блоха.

${\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}$

который имеет термины для прецессии, релаксации T2 и релаксации T1.

В 1956 году Х.К. Торри математически показал, как уравнения Блоха для намагничивания изменятся при добавлении диффузии. Торри модифицировал первоначальное описание поперечной намагниченности Блоха, включив в него диффузионные условия и применение пространственно изменяющегося градиента. Поскольку намагниченность $M$ — вектор, существует три уравнения диффузии, по одному на каждое измерение. Уравнение Блоха -Торри :

${\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}+\nabla \cdot {\vec {D}}\nabla {\vec {M}}$

где ${\vec {D}}$ теперь является тензором диффузии.

В простейшем случае, когда диффузия изотропна, тензор диффузии кратен единице:

${\vec {D}}=D\cdot {\vec {I}}=D\cdot {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},$

тогда уравнение Блоха-Торри будет иметь решение

${M}={M}_{\text{bloch}}e^{-{\frac {1}{3}}\gamma ^{2}G^{2}t^{3}D}\sim e^{-bD_{0}}$

Экспоненциальный член будет называться затуханием $A$. Анизотропная диффузия будет иметь аналогичное решение для тензора диффузии, за исключением того, что будет измеряться кажущийся коэффициент диффузии (ADC). В целом затухание такое:

$A=e^{-\sum _{i,j}b_{ij}D_{ij}}$

где $b_{ij}$ термины включают поля градиента $G_{x}$, $G_{y}$, и $G_{z}$.

Оттенки серого

Стандартная шкала серого для изображений DWI должна представлять повышенное ограничение диффузии как более яркое.

Изображение АЦП

Изображение ADC того же случая инфаркта головного мозга, что и при DWI в разделе выше.

Изображение кажущегося коэффициента диффузии (ADC), или карта ADC , представляет собой изображение МРТ, которое более конкретно показывает диффузию, чем обычный DWI, за счет устранения взвешивания T2 , которое в противном случае присуще обычному DWI. Визуализация ADC осуществляется путем получения нескольких традиционных изображений DWI с разной степенью взвешивания DWI, при этом изменение сигнала пропорционально скорости диффузии. В отличие от изображений DWI, стандартные оттенки серого изображений ADC должны представлять меньшую величину диффузии как более темную.

Инфаркт головного мозга приводит к ограничению диффузии, поэтому разница между изображениями с различным весом DWI будет незначительной, что приведет к изображению ADC с низким сигналом в зоне инфаркта. Снижение ADC может быть обнаружено через несколько минут после инфаркта мозга. Высокий сигнал пораженной ткани при обычном ДВИ является результатом частичного Т2-взвешивания.

Диффузионно-тензорная визуализация

Диффузионно-тензорная визуализация (DTI) — это метод магнитно-резонансной томографии, который позволяет измерять ограниченную диффузию воды в тканях для получения изображений нервных путей вместо использования этих данных исключительно с целью присвоения контраста или цвета пикселям в кресте. - изображение в разрезе. Он также предоставляет полезную структурную информацию о мышцах, включая сердечную мышцу, а также о других тканях, таких как простата.

В DTI каждый воксель имеет одну или несколько пар параметров: скорость диффузии и предпочтительное направление диффузии, описываемое в терминах трехмерного пространства, для которого этот параметр действителен. Свойства каждого воксела одного изображения DTI обычно рассчитываются с помощью векторной или тензорной математики на основе шести или более различных диффузионно-взвешенных измерений, каждый из которых получен с разной ориентацией градиентов, сенсибилизирующих диффузию. В некоторых методах выполняются сотни измерений, каждое из которых составляет полное изображение, для создания единого результирующего набора расчетных данных изображения. Более высокое информационное содержание воксела DTI делает его чрезвычайно чувствительным к едва заметным патологиям в мозге. Кроме того, информацию о направлении можно использовать на более высоком уровне структуры для выбора и отслеживания нервных путей через мозг — процесс, называемый трактографией .

Более точная формулировка процесса получения изображения состоит в том, что интенсивность изображения в каждой позиции ослабляется в зависимости от силы ( значения b ) и направления так называемого градиента магнитной диффузии, а также от локальной микроструктуры, в которой Молекулы воды диффундируют. Чем более ослаблено изображение в данной позиции, тем больше диффузия в направлении градиента диффузии. Чтобы измерить полный профиль диффузии ткани, необходимо повторить МР-сканирование, применяя разные направления (и, возможно, силу) градиента диффузии для каждого сканирования.

Математическая основа — тензоры.

См. Также: Теорема о главной оси.

Диффузионная МРТ опирается на математические и физические интерпретации геометрических величин, известных как тензоры . К изображению имеет отношение только частный случай общего математического понятия, основанный на понятии симметричной матрицы . Диффузия сама по себе является тензорной, но во многих случаях цель на самом деле состоит не в том, чтобы попытаться изучить диффузию мозга как таковую, а в том, чтобы просто попытаться воспользоваться преимуществами диффузионной анизотропии в белом веществе с целью определения ориентации аксонов и величины или степень анизотропии. Тензоры имеют реальное физическое существование в материале или ткани, поэтому они не перемещаются при вращении системы координат, используемой для их описания. Существует множество различных возможных представлений тензора (ранга 2), но среди них в этом обсуждении основное внимание уделяется эллипсоиду из-за его физической значимости для диффузии и из-за его исторического значения в развитии визуализации диффузионной анизотропии в МРТ.

Следующая матрица отображает компоненты тензора диффузии:

${\bar {D}}={\begin{vmatrix}D_{\color {red}xx}&D_{xy}&D_{xz}\\D_{xy}&D_{\color {red}yy}&D_{yz}\\D_{xz}&D_{yz}&D_{\color {red}zz}\end{vmatrix}}$

Одна и та же матрица чисел может одновременно использоваться во второй раз для описания формы и ориентации эллипса, и та же матрица чисел может использоваться одновременно третьим способом в матричной математике для сортировки собственных векторов и собственных значений, как описано ниже.

Физические тензоры

Идея тензора в физической науке возникла из попыток описать количество физических свойств. Первыми свойствами, к которым они были применены, были те, которые можно описать одним числом, например температура. Свойства, которые можно описать таким образом, называются скалярами ; их можно считать тензорами ранга 0 или тензорами 0-го порядка. Тензоры также можно использовать для описания величин, имеющих направленность, таких как механическая сила. Эти величины требуют указания как величины, так и направления, и часто представляются вектором . Трехмерный вектор можно описать тремя компонентами: его проекцией на оси x, y и z . Векторы такого типа можно считать тензорами ранга 1 или тензорами 1-го порядка.

Тензор часто представляет собой физическое или биофизическое свойство, определяющее связь между двумя векторами. Когда к объекту прилагается сила, может возникнуть движение. Если движение происходит в одном направлении, трансформацию можно описать с помощью вектора — тензора ранга 1. Однако в ткани диффузия приводит к движению молекул воды по траекториям, которые с течением времени проходят в нескольких направлениях, что приводит к комплексная проекция на декартовы оси. Эта закономерность воспроизводима, если к одной и той же ткани одинаковым образом прикладывают одни и те же условия и силы. Если существует внутренняя анизотропная организация ткани, сдерживающая диффузию, то этот факт отразится на характере диффузии. Связь между свойствами движущей силы, вызывающей диффузию молекул воды, и результирующей закономерностью их движения в ткани можно описать тензором. Совокупность молекулярных смещений этого физического свойства можно описать девятью компонентами, каждый из которых связан с парой осей. хх , уу , zz , ху , ух , хз . zx , yz , зы , Их можно записать в виде матрицы, аналогичной той, что приведена в начале этого раздела.

Аналогично ведет себя диффузия от точечного источника в анизотропной среде белого вещества. Первый импульс диффузионного градиента Стейскала-Таннера эффективно маркирует некоторые молекулы воды, а второй импульс эффективно показывает их смещение вследствие диффузии. Каждое примененное направление градиента измеряет движение вдоль направления этого градиента. Шесть или более градиентов суммируются, чтобы получить все измерения, необходимые для заполнения матрицы, при условии, что она симметрична выше и ниже диагонали (красные индексы).

в 1848 году. Анри Юро де Сенармон приложил нагретую точку к полированной поверхности кристалла, покрытой воском. В некоторых материалах, имевших «изотропную» структуру, кольцо расплава распространялось по поверхности по кругу. В анизотропных кристаллах разброс имел форму эллипса. В трех измерениях это распространение представляет собой эллипсоид. Как показал Адольф Фик в 1850-х годах, диффузия демонстрирует во многом те же закономерности, что и при передаче тепла.

Математика эллипсоидов

На этом этапе полезно рассмотреть математику эллипсоидов. Эллипсоид можно описать формулой: $ax^{2}+by^{2}+cz^{2}=1$. Это уравнение описывает квадратичную поверхность. Относительные значения a , b и c определяют, описывает ли квадрика эллипсоид или гиперболоид .

Как оказалось, еще три компонента можно добавить следующим образом: $ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy=1$. Многие комбинации a , b , c , d , e и f по-прежнему описывают эллипсоиды, но дополнительные компоненты ( d , e , f ) описывают вращение эллипсоида относительно ортогональных осей декартовой системы координат. Эти шесть переменных могут быть представлены матрицей, аналогичной тензорной матрице, определенной в начале этого раздела (поскольку диффузия симметрична, нам нужно только шесть компонентов вместо девяти — компоненты под диагональными элементами матрицы такие же, как и компоненты выше диагонали). Именно это имеется в виду, когда утверждается, что компоненты матрицы тензора второго порядка могут быть представлены эллипсоидом - если значения диффузии шести членов квадратичного эллипсоида помещены в матрицу, это порождает эллипсоид под углом вне ортогональной сетки. Его форма будет более вытянутой, если относительная анизотропия высока.

Когда эллипсоид/тензор представлен матрицей , мы можем применить полезный метод стандартной матричной математики и линейной алгебры, то есть « диагонализировать » матрицу. Это имеет два важных значения в визуализации. Идея состоит в том, что существуют два эквивалентных эллипсоида одинаковой формы, но разного размера и ориентации. Первый представляет собой измеренный эллипсоид диффузии, расположенный под углом, определяемым аксонами, а второй идеально выровнен по трем декартовым осям. Термин «диагонализация» относится к трем компонентам матрицы по диагонали от верхнего левого угла к нижнему правому (компоненты с красными индексами в матрице в начале этого раздела). Переменные $ax^{2}$, $by^{2}$, и $cz^{2}$ расположены по диагонали (красные индексы), но переменные d , e и f находятся «вне диагонали». Затем становится возможным выполнить этап векторной обработки, на котором мы переписываем нашу матрицу и заменяем ее новой матрицей, умноженной на три разных вектора единичной длины (длина = 1,0). Матрица диагонализуется, поскольку все недиагональные компоненты теперь равны нулю. Углы поворота, необходимые для достижения этого эквивалентного положения, теперь отображаются в трех векторах и могут быть считаны как компоненты x , y и z каждого из них. Эти три вектора называются « собственными векторами » или характеристическими векторами. Они содержат информацию об ориентации исходного эллипсоида. Три оси эллипсоида теперь расположены прямо вдоль главных ортогональных осей системы координат, поэтому мы можем легко определить их длину. Эти длины являются собственными значениями или характеристическими значениями.

Диагонализация матрицы осуществляется путем нахождения второй матрицы, на которую ее можно умножить, с последующим умножением на обратную вторую матрицу, при этом результатом является новая матрица, в которой три диагональных ( xx , yy , zz компонента ) имеют числа в их, но недиагональные компоненты ( xy , yz , zx ) равны 0. Вторая матрица предоставляет о собственном векторе информацию .

Меры анизотропии и диффузии

Визуализация данных DTI с помощью эллипсоидов.

В современной клинической неврологии различные патологии головного мозга лучше всего можно обнаружить, рассматривая конкретные показатели анизотропии и диффузии. Основной физический процесс диффузии заставляет группу молекул воды выходить из центральной точки и постепенно достигать поверхности эллипсоида, если среда анизотропна (для изотропной среды это была бы поверхность сферы). Формализм эллипсоида действует также как математический метод организации тензорных данных. Измерение тензора эллипсоида дополнительно позволяет провести ретроспективный анализ и собрать информацию о процессе диффузии в каждом вокселе ткани.

В изотропной среде, такой как спинномозговая жидкость , молекулы воды движутся за счет диффузии и движутся с одинаковой скоростью во всех направлениях. мы можем создать формулу, которая позволит нам преобразовать затухание сигнала воксела МРТ в числовую меру диффузии — коэффициент диффузии D. Зная детальное влияние градиентов диффузии , Когда различные барьеры и ограничивающие факторы, такие как клеточные мембраны и микротрубочки, мешают свободной диффузии, мы измеряем «кажущийся коэффициент диффузии», или ADC , поскольку при измерении не учитываются все локальные эффекты, и затухание рассматривается так, как если бы все скорости движения были исключительно за счет броуновского движения . АЦП в анизотропной ткани варьируется в зависимости от направления, в котором он измеряется. Диффузия происходит быстро по длине аксона (параллельно ему) и медленнее перпендикулярно поперек него.

После того, как мы измерили воксель в шести или более направлениях и скорректировали затухания из-за эффектов T2 и T1, мы можем использовать информацию из нашего рассчитанного тензора эллипсоида для описания того, что происходит в вокселе. Если вы рассматриваете эллипсоид, расположенный под углом в декартовой сетке, вы можете рассмотреть проекцию этого эллипса на три оси. Три проекции могут дать вам АЦП по каждой из трех осей: ADC _x , ADC _y , ADC _z . Это приводит к идее описания средней диффузии в вокселе, которая будет просто

$(ADC_{x}+ADC_{y}+ADC_{z})/3=ADC_{i}$

Мы используем индекс i , чтобы указать, что именно таким будет коэффициент изотропной диффузии с усредненным эффектом анизотропии.

Сам эллипсоид имеет главную длинную ось, а затем еще две меньшие оси, которые описывают его ширину и глубину. Все три из них перпендикулярны друг другу и пересекаются в центральной точке эллипсоида. В этом случае мы называем оси собственными векторами , а меры их длин — собственными значениями . Длины обозначаются греческой буквой λ . Длинная из них, направленная в направлении аксона, будет λ ₁ , а две маленькие оси будут иметь длины λ ₂ и λ ₃ . В условиях тензорного эллипсоида DTI мы можем рассматривать каждый из них как меру коэффициента диффузии вдоль каждой из трех основных осей эллипсоида. Это немного отличается от АЦП, поскольку это была проекция на ось, а λ — это фактическое измерение рассчитанного нами эллипсоида.

Коэффициент диффузии вдоль главной оси λ ₁ также называют продольным коэффициентом диффузии, или осевым коэффициентом диффузии , или даже параллельным коэффициентом диффузии λ _∥ . Исторически это наиболее близко к тому, что Ричардс первоначально измерил длину вектора в 1991 году. Коэффициенты диффузии по двум малым осям часто усредняются, чтобы получить меру радиального коэффициента диффузии.

$\lambda _{\perp }=(\lambda _{2}+\lambda _{3})/2.$

Эта величина является оценкой степени ограничения из-за мембран и других эффектов и оказывается чувствительным показателем дегенеративной патологии при некоторых неврологических состояниях. Его также можно назвать перпендикулярной диффузией ( $\lambda _{\perp }$).

Другой часто используемой мерой, которая суммирует общую диффузионную способность, является след , который представляет собой сумму трех собственных значений:

$\mathrm {tr} (\Lambda )=\lambda _{1}+\lambda _{2}+\lambda _{3}$

где $\Lambda$ представляет собой диагональную матрицу с собственными значениями $\lambda _{1}$, $\lambda _{2}$ и $\lambda _{3}$ на его диагонали.

Если мы разделим эту сумму на три, мы получим средний коэффициент диффузии :

$\mathrm {MD} =(\lambda _{1}+\lambda _{2}+\lambda _{3})/3$

что равно АЦП _i, поскольку

${\begin{aligned}\mathrm {tr} (\Lambda )/3&=\mathrm {tr} (V^{-1}V\Lambda )/3\\&=\mathrm {tr} (V\Lambda V^{-1})/3\\&=\mathrm {tr} (D)/3\\&=ADC_{i}\end{aligned}}$

где $V$ – матрица собственных векторов и $D$ – тензор диффузии.Помимо описания степени диффузии, часто важно описать относительную степень анизотропии вокселя. На одном полюсе будет сфера изотропной диффузии, а на другом полюсе будет очень тонкий вытянутый сфероид в форме сигары или карандаша . Простейшая мера получается путем деления самой длинной оси эллипсоида на самую короткую = ( λ ₁ / λ ₃ ). Однако это оказывается очень чувствительным к шуму измерений, поэтому были разработаны все более сложные меры для улавливания измерения при минимизации шума. Важным элементом этих расчетов является сумма квадратов разностей коэффициентов диффузии = ( λ ₁ − λ ₂ ) ² + ( λ ₁ - λ ₃ ) ² + ( λ ₂ - λ ₃ ) ² . Мы используем квадратный корень из суммы квадратов, чтобы получить своего рода средневзвешенное значение, в котором доминирует наибольший компонент. Одна из целей — поддерживать число около 0, если воксель сферический, и около 1, если он вытянутый. Это приводит к дробной анизотропии или FA , которая представляет собой квадратный корень из суммы квадратов (SRSS) разностей коэффициентов диффузии, разделенной на SRSS коэффициентов диффузии. Когда вторая и третья оси малы относительно главной оси, число в числителе почти равно числу в знаменателе. Мы также умножаем на $1/{\sqrt {2}}$ так что максимальное значение FA равно 1. Вся формула для FA выглядит следующим образом:

$\mathrm {FA} ={\frac {\sqrt {3((\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2})}}{\sqrt {2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}$

где ${\textstyle \operatorname {E} [\lambda ]=(\lambda _{1}+\lambda _{2}+\lambda _{3})/3\,.}$

Дробную анизотропию также можно разделить на линейную, плоскую и сферическую меры в зависимости от «формы» диффузионного эллипсоида. Например, вытянутый эллипсоид в форме «сигары» указывает на сильно линейную анизотропию, «летающая тарелка» или сплюснутый сфероид представляет собой диффузию в плоскости, а сфера указывает на изотропную диффузию, одинаковую во всех направлениях. Если собственные значения вектора диффузии отсортированы так, что $\lambda _{1}\geq \lambda _{2}\geq \lambda _{3}\geq 0$, то меры можно рассчитать следующим образом:

Для линейного случая , где $\lambda _{1}\gg \lambda _{2}\simeq \lambda _{3}$,

$C_{l}={\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}$

Для плоского случая , когда $\lambda _{1}\simeq \lambda _{2}\gg \lambda _{3}$,

$C_{p}={\frac {2(\lambda _{2}-\lambda _{3})}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}$

Для сферического случая , где $\lambda _{1}\simeq \lambda _{2}\simeq \lambda _{3}$,

$C_{s}={\frac {3\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}$

Каждая мера находится между 0 и 1, а их сумма равна единице. дополнительную меру анизотропии Для описания отклонения от сферического случая можно использовать :

$C_{a}=C_{l}+C_{p}=1-C_{s}={\frac {\lambda _{1}+\lambda _{2}-2\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}$

Используются и другие показатели анизотропии, включая относительную анизотропию (RA):

$\mathrm {RA} ={\frac {\sqrt {(\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2}}}{{\sqrt {3}}\operatorname {E} [\lambda ]}}$

и объемный коэффициент (VR):

$\mathrm {VR} ={\frac {\lambda _{1}\lambda _{2}\lambda _{3}}{\operatorname {E} [\lambda ]^{3}}}$

Приложения

Наиболее распространенное применение обычного DWI (без DTI) – при острой ишемии головного мозга. ДВИ непосредственно визуализирует ишемический некроз при инфаркте мозга в виде цитотоксического отека, проявляется в виде высокого сигнала DWI в течение нескольких минут после артериальной окклюзии. Если перфузионная МРТ выявляет как сердцевину инфаркта, так и полутень , которую можно спасти , последнюю можно количественно оценить с помощью DWI и перфузионной МРТ.

• 
  DWI показывает некроз (показан более ярким) при инфаркте головного мозга.
• 
  DWI демонстрирует ограниченную диффузию в медиальном дорсальном таламусе, что соответствует энцефалопатии Вернике
• 
  DWI демонстрирует высокий кортикальный лентообразный сигнал, соответствующий ограничению диффузии у пациента с известным синдромом MELAS

Другая область применения DWI – онкология . Опухоли во многих случаях являются высококлеточными, что обеспечивает ограниченную диффузию воды и поэтому проявляется с относительно высокой интенсивностью сигнала при DWI. ДВИ обычно используется для обнаружения и определения стадии опухолей, а также для мониторинга реакции опухоли на лечение с течением времени. DWI также может быть собран для визуализации всего тела с использованием метода, называемого «диффузионно-взвешенная визуализация всего тела с подавлением фонового сигнала тела» (DWIBS). Было также показано, что некоторые более специализированные методы диффузионной МРТ, такие как диффузионная эксцессная визуализация (DKI), позволяют прогнозировать реакцию онкологических больных на химиотерапию.

Основное применение — визуализация белого вещества , при которой можно измерить расположение, ориентацию и анизотропию трактов. Архитектура аксонов в параллельных пучках и их миелиновые оболочки облегчают диффузию молекул воды преимущественно в их основном направлении. Такая преимущественно ориентированная диффузия называется анизотропной диффузией .

Трактографическая реконструкция нейронных связей с помощью DTI

ДТИ плечевого сплетения здорового человека. Взято из Wade et al., 2020.

Визуализация этого свойства является продолжением диффузионной МРТ. Если применяется серия диффузионных градиентов (т. е. вариаций магнитного поля в магните МРТ), которые могут определить как минимум 3 вектора направления (использование 6 различных градиентов является минимумом, а дополнительные градиенты повышают точность «недиагональной» информации), можно вычислить для каждого воксела тензор 3×3) , (т.е. симметричную положительно определенную матрицу который описывает трехмерную форму диффузии. тензора Направление волокна указывается главным собственным вектором . Этот вектор может иметь цветовую кодировку, что дает картографию положения и направления трактов (красный для левого-правого, синий для верхнего-нижнего и зеленый для переднего-заднего). Яркость взвешивается дробной анизотропией, которая является скалярной мерой степени анизотропии в данном вокселе. Средняя диффузия (MD) или след — это скалярная мера общей диффузии внутри вокселя. Эти меры обычно используются в клинике для локализации поражений белого вещества, которые не обнаруживаются при других формах клинической МРТ.

Применение в мозге:

• Трактоспецифическая локализация поражений белого вещества при травме и определение тяжести диффузной черепно-мозговой травмы . Локализация опухолей по отношению к трактам белого вещества (инфильтрация, отклонение) была одним из наиболее важных первоначальных применений. При планировании хирургического лечения некоторых типов опухолей головного мозга необходимо знать близость и взаимное расположение кортикоспинального тракта и опухоли.
• Данные диффузионно-тензорной визуализации можно использовать для выполнения трактографии белого вещества. Алгоритмы отслеживания волокон можно использовать для отслеживания волокна по всей его длине (например, кортикоспинальный тракт , по которому двигательная информация передается от моторной коры к спинному мозгу и периферическим нервам ). Трактография — полезный инструмент для измерения дефицита белого вещества, например, при старении. Его оценка ориентации и силы волокон становится все более точной и имеет широкое потенциальное применение в областях когнитивной нейробиологии и нейробиологии.
• Использование DTI для оценки развития, патологии и дегенерации белого вещества было в центре внимания более 2500 научных публикаций с 2005 года. Оно обещает быть очень полезным для дифференциации болезни Альцгеймера от других типов деменции . Приложения в исследованиях мозга включают исследование нейронных сетей in vivo , а также в коннектомике .

Применение для периферических нервов:

• Плечевое сплетение : DTI может дифференцировать нормальные нервы. (как показано на трактограмме спинного мозга и плечевого сплетения и 3D 4k реконструкции здесь ) из травматически поврежденных нервных корешков.
• Синдром кубитального канала : показатели, полученные из DTI (FA и RD), могут отличить бессимптомных взрослых от людей со сдавлением локтевого нерва в локтевом суставе.
• Синдром запястного канала : показатели, полученные из DTI (нижний FA и MD), отличают здоровых взрослых от людей с синдромом запястного канала.

Исследовать

На ранних этапах разработки трактографии на основе DTI ряд исследователей указали на недостаток модели тензора диффузии. Тензорный анализ предполагает, что в каждом вокселе изображения имеется один эллипсоид — как если бы все аксоны, проходящие через воксель, двигались в одном и том же направлении. Часто это так, но можно подсчитать, что более чем в 30% вокселей изображения мозга стандартного разрешения присутствуют как минимум два разных нервных тракта, движущихся в разных направлениях и проходящих друг через друга. В классической модели тензора эллипсоида диффузии информация от пересекающего тракта выглядит как шум или необъяснимое уменьшение анизотропии в данном вокселе.

Дэвид Тач был одним из первых, кто описал решение этой проблемы. Идею лучше всего понять, если концептуально разместить своего рода геодезический купол вокруг каждого вокселя изображения. Этот икосаэдр обеспечивает математическую основу для прохождения большого количества равномерно расположенных градиентных траекторий через воксель, каждая из которых совпадает с одной из вершин икосаэдра. Затем мы можем посмотреть на воксель с большого количества разных направлений (обычно 40 или более). Мы используем « n -кортежей» мозаику , чтобы добавить более равномерно расположенные вершины к исходному икосаэдру (20 граней) — идея, которая также имела прецеденты в исследованиях палеомагнетизма несколькими десятилетиями ранее. Мы хотим знать, какие направляющие линии вызывают максимальные меры анизотропной диффузии. Если имеется один тракт, то будет только два максимума, направленных в противоположные стороны. Если в вокселе пересекаются два тракта, то будет две пары максимумов и так далее. Мы по-прежнему можем использовать тензорную математику, чтобы использовать максимумы для выбора групп градиентов для упаковки в несколько разных тензорных эллипсоидов в одном и том же вокселе, или использовать более сложный тензорный анализ более высокого ранга, или мы можем провести настоящий анализ без использования моделей, который выберет максимумы, а затем продолжим трактографию.

Метод трактографии Q-Ball — это реализация, в которой Дэвид Тач предлагает математическую альтернативу тензорной модели. Вместо того, чтобы объединять данные диффузионной анизотропии в группу тензоров, используемая математика использует как распределения вероятностей, так и классическую геометрическую томографию и векторную математику, разработанную почти 100 лет назад — преобразование Фанка-Радона .

Обратите внимание, что продолжаются споры о том, как лучше всего предварительно обрабатывать результаты ДВ-МРТ. Несколько исследований in vivo показали, что выбор программного обеспечения и применяемых функций (направленных на коррекцию артефактов, возникающих, например, из-за движения и вихревых токов) оказывают существенное влияние на оценки параметров DTI по ​​ткани. Следовательно, это тема многонационального исследования, проводимого группой диффузионных исследований ISMRM.

Краткое содержание

Для DTI обычно можно использовать линейную алгебру , матричную математику и векторную математику для обработки анализа тензорных данных.

В некоторых случаях интерес представляет полный набор свойств тензора, но для трактографии обычно необходимо знать только величину и ориентацию первичной оси или вектора. Эта первичная ось — та, которая имеет наибольшую длину — является самым большим собственным значением, и ее ориентация закодирована в соответствующем собственном векторе. Для выполнения трактографии необходима только одна ось, поскольку предполагается, что наибольшее собственное значение совпадает с направлением основного аксона.

См. также

• Коннектограмма
• Коннектом
• Трактография

Внешние ссылки

• PNRC: О диффузионной МРТ
• Атлас белого вещества