Сфера холма

Чтобы узнать о внутренней части облака Оорта, см. Облако Холмов .

В разрезе/виде сбоку двухмерное представление трехмерной концепции сферы Хилла, здесь показан «гравитационный колодец» Земли (гравитационный потенциал Земли, синяя линия), то же самое для Луны (красная линия) и их совокупный потенциал (черная толстая линия). Точка P — это свободное от сил место, где гравитационные силы Земли и Луны компенсируются. Размеры Земли и Луны пропорциональны, но расстояния и энергии не в масштабе.

Сфера Хилла является распространенной моделью для расчета гравитационной сферы влияния . Это наиболее часто используемая модель для расчета пространственной степени гравитационного влияния астрономического тела ( m ), в которой оно доминирует над гравитационным влиянием других тел, особенно основного ( M ). Иногда ее путают с другими моделями гравитационного воздействия, такими как сфера Лапласа. или сферой Роша , причем последняя вызывает путаницу с пределом Роша . Он был определен американским астрономом Джорджем Уильямом Хиллом на основе работы французского астронома Эдуарда Роша .

Чтобы удержаться более гравитационно притягивающим астрофизическим объектом — планетой — более массивной звездой, луной — более массивной планетой, — менее массивное тело должно иметь орбиту , находящуюся в пределах гравитационного потенциала, представленного сферой Хилла более массивного тела. Эта луна, в свою очередь, будет иметь собственную сферу Хилла, и любой объект на этом расстоянии будет стремиться стать спутником Луны, а не самой планеты.

Контурный график эффективного гравитационного потенциала системы двух тел, здесь Солнца и Земли, с указанием пяти точек Лагранжа .

Одним из простых представлений о размерах Солнечной системы является то, что она ограничена сферой Хилла Солнца ( порожденной взаимодействием Солнца с ядром галактики или другими более массивными звездами). Более сложным примером является тот, что справа, сфера Земного холма, которая простирается между точками Лагранжа L ₁ и L ₂ , которые лежат вдоль линии центров Земли и более массивного Солнца. Гравитационное влияние менее массивного тела в этом направлении минимально, поэтому оно действует как ограничивающий фактор для размера сферы Хилла; за пределами этого расстояния третий объект на орбите вокруг Земли проведет по крайней мере часть своей орбиты за пределами сферы Хилла и будет постепенно возмущаться приливными силами более массивного тела, Солнца, и в конечном итоге окажется на орбите последнего.

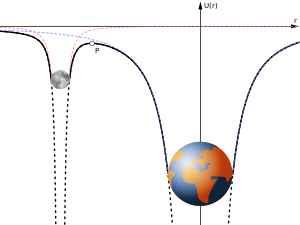
Для двух массивных тел с гравитационными потенциалами и любой заданной энергии взаимодействующего с ними третьего объекта незначительной массы можно определить в пространстве поверхность с нулевой скоростью , которую невозможно преодолеть, — контур интеграла Якоби . Когда энергия объекта мала, поверхность с нулевой скоростью полностью окружает менее массивное тело (этой ограниченной системы трех тел ), а это означает, что третий объект не может убежать; при более высокой энергии будет один или несколько пробелов или узких мест, через которые третий объект сможет покинуть менее массивное тело и выйти на орбиту вокруг более массивного. Если энергия находится на границе между этими двумя случаями, то третий объект не может ускользнуть, но ограничивающая его поверхность с нулевой скоростью касается большей поверхности с нулевой скоростью вокруг менее массивного тела. в одной из близлежащих точек Лагранжа, образуя там конусообразную точку. На противоположной стороне менее массивного тела поверхность нулевой скорости приближается к другой точке Лагранжа. Эта ограничивающая поверхность с нулевой скоростью вокруг менее массивного тела является его «сферой» Хилла.

Определение

Радиус холма или сфера (последний определяется первым радиусом ) описывается как «область вокруг планетарного тела, где собственная гравитация (по сравнению с гравитацией Солнца или других близлежащих тел) является доминирующей силой притяжения спутников», как естественных, так и искусственных.

По описанию де Патера и Лиссауэра, все тела в такой системе, как Солнечная система Солнца , «чувствуют гравитационную силу друг друга», и хотя движения всего лишь двух гравитационно взаимодействующих тел, составляющие «проблему двух тел», «полностью интегрируемый ([значение] ... существует один независимый интеграл или ограничение на степень свободы)» и, следовательно, точное аналитическое решение, взаимодействия трех (или более) таких тел «не могут быть выведены аналитически», требуя вместо этого решения путем численного интегрирования, если это возможно. Это так, если только незначительная масса одного из трех тел не позволяет аппроксимировать систему как задачу двух тел, формально известную как «ограниченная задача трех тел».

Для таких задач двух или ограниченных трех тел, как их простейшие примеры — например, еще одно массивное первичное астрофизическое тело, масса m1, и менее массивное вторичное тело, масса m2 — концепция радиуса или сферы Хилла имеет самое важное значение. приблизительный предел «гравитационного доминирования» вторичной массы, предел, определяемый «протяженностью» сферы Хилла, которая математически представляется следующим образом:

$R_{\mathrm {H} }\approx a{\sqrt[{3}]{\frac {m_{2}}{3(m_{1}+m_{2})}}}$,

где в этом представлении большую ось «а» можно понимать как «мгновенное гелиоцентрическое расстояние» между двумя массами (в других местах сокращенно r p ).

В более общем смысле, если менее массивное тело, $m2$, вращается вокруг более массивного тела (например, m1, как планеты, вращающейся вокруг Солнца) и имеет большую полуось $a$и эксцентриситет ​ $e$, то радиус или сфера Хилла, $R_{\mathrm {H} }$ менее массивного тела, рассчитанная в перицентре , составляет примерно:

$R_{\mathrm {H} }\approx a(1-e){\sqrt[{3}]{\frac {m_{2}}{3(m_{1}+m_{2})}}}.$

Когда эксцентриситет пренебрежимо мал (наиболее благоприятный случай для устойчивости орбиты), это выражение сводится к представленному выше.

Пример и вывод

Схематическое изображение сфер Хилла (как двумерных радиусов) и пределов Роша каждого тела системы Солнце-Земля-Луна не в масштабе. Фактический радиус Хилла для пары Земля-Луна составляет порядка 60 000 км (т. е. занимает менее одной шестой расстояния в 378 000 км между Луной и Землей).

В примере Земля-Солнце Земля ( 5,97 × 10 ²⁴ кг ) вращается вокруг Солнца ( 1,99 × 10 ³⁰ кг ) на расстоянии 149,6 млн км, или одна астрономическая единица (а.е.). Таким образом, сфера Хилла Земли простирается примерно на 1,5 миллиона км (0,01 а.е.). Орбита Луны, находящаяся на расстоянии 0,384 миллиона км от Земли, удобно находится в гравитационной сфере влияния Земли, и поэтому ей не грозит риск быть вытянутой на независимую орбиту вокруг Солнца.

Предыдущую формулу игнорирования эксцентриситета можно переформулировать следующим образом:

${\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx 1/3{\frac {m2}{M}}$, или $3{\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx {\frac {m2}{M}}$,

где М — сумма взаимодействующих масс.

Вывод

Выражение для радиуса Хилла можно найти, приравнивая гравитационную и центробежную силы, действующие на пробную частицу (с массой намного меньшей, чем $m$) вращается вокруг вторичного тела. Предположим, что расстояние между массами $M$ и $m$ является $r$, и что пробная частица вращается на расстоянии $r_{\mathrm {H} }$ из вторичного. Когда пробная частица находится на линии, соединяющей первичное и вторичное тела, баланс сил требует, чтобы

${\frac {Gm}{r_{\mathrm {H} }^{2}}}-{\frac {GM}{(r-r_{\mathrm {H} })^{2}}}+\Omega ^{2}(r-r_{\mathrm {H} })=0,$

где $G$ гравитационная постоянная и $\Omega ={\sqrt {\frac {GM}{r^{3}}}}$ - ( кеплеровская ) угловая скорость вторичной обмотки относительно первичной (при условии, что $m\ll M$). Приведенное выше уравнение также можно записать как

${\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)^{-2}+{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)=0,$

который посредством биномиального разложения до ведущего порядка в $r_{\mathrm {H} }/r$, можно записать как

${\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(1+2{\frac {r_{\mathrm {H} }}{r}}\right)+{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)={\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(3{\frac {r_{\mathrm {H} }}{r}}\right)\approx 0.$

Следовательно, указанное выше соотношение

${\frac {r_{\mathrm {H} }}{r}}\approx {\sqrt[{3}]{\frac {m}{3M}}}.$

Если орбита вторичного компонента вокруг первичного эллиптическая, то радиус Хилла максимален в апоцентре , где $r$ наибольшее и минимальное в перицентре орбиты. Следовательно, в целях стабильности пробных частиц (например, небольших спутников) необходимо учитывать радиус Хилла на расстоянии перицентра.

Для наведения порядка в $r_{\mathrm {H} }/r$, радиус Хилла выше также представляет собой расстояние точки Лагранжа L ₁ от вторичной обмотки.

Регионы стабильности

Сфера Хилла является лишь приближением, и другие силы (такие как давление излучения или эффект Ярковского ) могут в конечном итоге вывести объект из сферы. Как уже говорилось, спутник (третья масса) должен быть достаточно мал, чтобы его гравитация вносила незначительный вклад.

Детальные численные расчеты показывают, что орбиты на сфере Хилла или внутри нее не стабильны в долгосрочной перспективе; оказывается, что стабильные спутниковые орбиты существуют только в пределах от 1/2 до 1/3 радиуса Хилла.

Область устойчивости ретроградных орбит на большом расстоянии от главной звезды больше, чем область устойчивости прямых орбит на большом расстоянии от главной звезды. Считалось, что этим объясняется преобладание ретроградных спутников вокруг Юпитера; однако у Сатурна более равномерное сочетание ретроградных и поступательных лун, поэтому причины более сложны.

Дальнейшие примеры

Сфера Хилла может быть настолько маленькой, что невозможно поддерживать орбиту вокруг тела. Например, астронавт не мог бы выйти на орбиту 104- тонного космического корабля "Шаттл" на орбите на высоте 300 км над Землей, потому что 104-тонный объект на этой высоте имеет сферу Хилла радиусом всего 120 см, что намного меньше, чем у космического корабля "Шаттл". Сфера такого размера и массы будет плотнее свинца , и действительно, на низкой околоземной орбите сферическое тело должно быть более плотным, чем свинец, чтобы поместиться внутри своей собственной сферы Хилла, иначе оно будет неспособно поддерживать орбиту. . Однако спутникам, находящимся дальше на геостационарной орбите , потребуется всего лишь более 6% плотности воды, чтобы поместиться внутри их собственной сферы Хилла.

В Солнечной системе планета с самым большим радиусом холма — Нептун — 116 миллионов км, или 0,775 а.е.; его большое расстояние от Солнца вполне компенсирует его небольшую массу по сравнению с Юпитером (радиус собственного холма которого составляет 53 миллиона км). Астероид 1 из пояса астероидов будет иметь сферу Хилла, которая может достигать 220 000 км (для Цереры ), быстро уменьшаясь с уменьшением массы. Сфера Хилла 66391 Мошуп , астероида, пересекающего Меркурий и имеющего спутник (названный Скваннит), имеет радиус 22 км.

Типичный внесолнечный « горячий Юпитер », HD 209458 b . имеет радиус сферы Хилла 593 000 км, что примерно в восемь раз больше его физического радиуса (около 71 000 км). Даже самая маленькая внесолнечная планета, CoRoT-7b , по-прежнему имеет радиус сферы Хилла (61 000 км), что в шесть раз превышает его физический радиус (около 10 000 км). Следовательно, у этих планет могут быть небольшие спутники поблизости, хотя и за пределами их соответствующих пределов Роша .

Сферы холмов для Солнечной системы

В следующей таблице и логарифмическом графике показаны радиусы сфер Хилла некоторых тел Солнечной системы, рассчитанные по первой формуле, указанной выше (включая эксцентриситет орбиты), с использованием значений, полученных из эфемерид JPL DE405 и с веб-сайта NASA Solar System Exploration.

Радиус сфер холмов некоторых тел Солнечной системы

Тело	Миллион км	В	Радиусы тела	Угловые минуты	Самая дальняя луна (ау)
Меркурий	0.1753	0.0012	71.9	10.7	—
Венера	1.0042	0.0067	165.9	31.8	—
Земля	1.4714	0.0098	230.7	33.7	0.00257
Марс	0.9827	0.0066	289.3	14.9	0.00016
Юпитер	50.5736	0.3381	707.4	223.2	0.1662
Сатурн	61.6340	0.4120	1022.7	147.8	0.1785
Уран	66.7831	0.4464	2613.1	80.0	0.1366
Нептун	115.0307	0.7689	4644.6	87.9	0.3360
Церера	0.2048	0.0014	433.0	1.7	—
Плутон	5.9921	0.0401	5048.1	3.5	0.00043
Эрис	8.1176	0.0543	6979.9	2.7	0.00025

Логарифмический график радиусов Хилла (в км) для тел Солнечной системы

См. также

• Межпланетная транспортная сеть
• телом проблема с
• доля Роша
• Сфера влияния (астродинамика)
• Сфера влияния (черная дыра)

Дальнейшее чтение

• де Патер, Имке и Лиссауэр, Джек (2015). «Динамика (задача трех тел, возмущения и резонансы)». Планетарные науки (2-е изд.). Кембридж, Англия: Издательство Кембриджского университета. стр. 28–30, 34. ISBN.  9781316195697 . Проверено 22 июля 2023 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• де Патер, Имке и Лиссауэр, Джек (2015). «Планетообразование (Образование планет-гигантов, спутников планет и малых планет)». Планетарные науки (2-е изд.). Кембридж, Англия: Издательство Кембриджского университета. стр. 539, 544. ISBN.  9781316195697 . Проверено 22 июля 2023 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Гурзадян, Григор А. (2020). «Сфера притяжения, сфера действия и сфера Хилла». Теория межпланетных полетов . Бока-Ратон, Флорида: CRC Press. стр. 258–263. ISBN  9781000116717 . Проверено 22 июля 2023 г.
• Гурзадян, Григор А. (2020). «Предел Роша». Теория межпланетных полетов . Бока-Ратон, Флорида: CRC Press. стр. 263ф. ISBN  9781000116717 . Проверено 22 июля 2023 г.
• Ида, С.; Кокубо Э. и Такеда Т. (2012). «Моделирование аккреции Луны N-телами». В Марове Михаил Я. И Рикман, Ганс (ред.). Столкновительные процессы в Солнечной системе . Библиотека астрофизики и космических наук. Том. 261. Берлин, Германия: Springer Science & Business Media. стр. 206, 209 и далее. ISBN  9789401007122 . Проверено 22 июля 2023 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• ИП, В.-Х. и Фернандес, Дж. А. (2012). «Аккреционное происхождение гигантских планеров и его последствия». В Марове Михаил Я. И Рикман, Ганс (ред.). Столкновительные процессы в Солнечной системе . Библиотека астрофизики и космических наук. Том. 261. Берлин, Германия: Springer Science & Business Media. стр. 173f. ISBN  9789401007122 . Проверено 22 июля 2023 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Ашер, диджей; Бэйли, ME & Steel (2012). «Роль негравитационных сил в отделении орбит от Юпитера». В Марове Михаил Я. И Рикман, Ганс (ред.). Столкновительные процессы в Солнечной системе . Библиотека астрофизики и космических наук. Том. 261. Берлин, Германия: Springer Science & Business Media. п. 122. ИСБН  9789401007122 . Проверено 22 июля 2023 г. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

Внешние ссылки

• Может ли астронавт выйти на орбиту космического корабля?
• Луна, которая поднялась на холм, но спустилась с планеты. Архивировано 30 сентября 2008 г. в Wayback Machine.