5-симплекс

5-симплекс Гексатерон (хикс)
Тип	однородный 5-многогранник
Символ Шлефли	{3 ⁴}
Диаграмма Кокстера
4-ликий	6	6 {3,3,3}
Клетки	15	15 {3,3}
Лица	20	20 {3}
Края	15
Вершины	6
Вершинная фигура	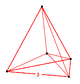5-клеточный
Группа Коксетера	А ₅ , [3 ⁴], порядок 720
Двойной	самодвойственный
Базовая точка	(0,0,0,0,0,1)
Окружность	0.645497
Характеристики	выпуклый , изогональный , правильный , самодвойственный

В пятимерной геометрии 5- симплекс — это самодвойственный правильный 5-многогранник . Он имеет шесть вершин , 15 ребер , 20 треугольных граней , 15 тетраэдрических ячеек и 6 5-клеточных граней . Он имеет двугранный угол cos ⁻¹( ⁠ 1/5 . ⁠ ) , или примерно 78,46°

5-симплекс — это решение проблемы: сделайте 20 равносторонних треугольников, используя 15 спичек, где каждая сторона каждого треугольника равна ровно одной спичке.

Альтернативные названия

Его также можно назвать гексатероном или гекса-5-топом , как 6- гранный многогранник в 5-мерном пространстве. Название « гексатерон» происходит от слов «гекса-», обозначающего шесть граней , и «терон» ( тер- — искаженное слово «тетра-» ), обозначающего наличие четырёхмерных граней.

Джонатан Бауэрс дал гексатерону аббревиатуру hix . ^[1]

В качестве конфигурации

Эта матрица конфигурации представляет собой 5-симплекс. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам и 4-граням. Диагональные числа показывают, сколько каждого элемента встречается во всем 5-симплексе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного симплекса идентична его повороту на 180 градусов. ^[2]^[3]

${\begin{bmatrix}{\begin{matrix}6&5&10&10&5\\2&15&4&6&4\\3&3&20&3&3\\4&6&4&15&2\\5&10&10&5&6\end{matrix}}\end{bmatrix}}$

Декартовы координаты регулярного гексатерона

Гексатерон , можно построить из 5-клетки добавив 6-ю вершину так, чтобы она была равноудалена от всех остальных вершин 5-клетки.

Декартовы координаты вершин правильного гексатерона с центром в начале координат и длиной ребра 2:

{\begin{aligned}&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ {\tfrac {1}{\sqrt {3}}},\ \pm 1\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ -{\tfrac {2}{\sqrt {3}}},\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ -{\tfrac {\sqrt {3}}{\sqrt {2}}},\ 0,\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ -{\tfrac {2{\sqrt {2}}}{\sqrt {5}}},\ 0,\ 0,\ 0\right)\\[5pt]&\left(-{\tfrac {\sqrt {5}}{\sqrt {3}}},\ 0,\ 0,\ 0,\ 0\right)\end{aligned}}

Вершины 5-симплекса проще расположить на гиперплоскости в 6-мерном пространстве как перестановки (0,0,0,0,0,1) или (0,1,1,1,1,1). Эти конструкции можно рассматривать как грани 6-ортоплекса или выпрямленного 6-куба соответственно.

Проецируемые изображения

орфографические проекции
К Самолет Коксетера	A_А5	A ₄
График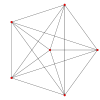
Двугранная симметрия	[6]	[5]
К Самолет Коксетера	A_А3	A_А2
График
Двугранная симметрия	[4]	[3]

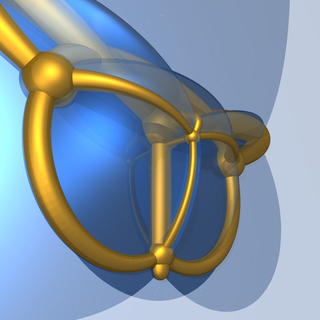Стереографическая проекция 4D на 3D диаграммы Шлегеля, 5D на 4D гексатерона.

Формы более низкой симметрии

Форма более низкой симметрии представляет собой 5-клеточную пирамиду {3,3,3}∨( ) с порядком симметрии [3,3,3] 120, построенную как 5-клеточное основание в 4-пространственной гиперплоскости и вершину точка над гиперплоскостью. Пять сторон пирамиды состоят из 5-клеточных клеток. Они рассматриваются как вершинные фигуры усеченных правильных 6-многогранников , например усеченного 6-куба .

Другая форма - {3,3}∨{ } с порядком симметрии [3,3,2,1] 48, соединение ортогонального двуугольника и тетраэдра, ортогонально смещенного, со всеми парами вершин, соединенных между собой. Другая форма - {3}∨{3} с [3,2,3,1] порядком симметрии 36 и расширенной симметрией [[3,2,3],1], порядком 72. Она представляет собой соединение двух ортогональных треугольников. , ортогонально смещенный, со всеми парами вершин, соединенных между собой.

Форма { }∨{ }∨{ } имеет симметрию [2,2,1,1] порядка 8, расширенную перестановкой 3 сегментов как [3[2,2],1] или [4,3,1,1 ], порядок 48.

Они видны в вершинных фигурах усеченных и триусеченных правильных 6 -многогранников, таких как усеченный побитно 6-куб и триусеченный 6-симплекс . Метки ребер здесь представляют типы граней в этом направлении и, таким образом, обозначают разные длины ребер.

Вершинная фигура всеусеченных 5-симплексных сот , , представляет собой 5-симплекс с циклом многоугольника Петри из 5 длинных ребер. Его симметрия изомофична группе диэдра Dih ₆ или группе простого вращения [6,2] ⁺, заказ 12.

Вершинные фигуры для однородных 6-многогранников
Присоединиться	{3,3,3}∨( )	{3,3}∨{ }	{3}∨{3}	{ }∨{ }∨{ }
Симметрия	[3,3,3,1] Заказать 120	[3,3,2,1] Заказ 48	[[3,2,3],1] Заказ 72	[3[2,2],1,1]=[4,3,1,1] Заказ 48	~[6] или ~[6,2] ⁺ Заказ 12
Диаграмма
Многогранник	усеченный 6-симплекс	усеченный 6-симплекс	усеченный 6-симплекс	Призма 3-3-3	Всеусеченные 5-симплексные соты

Сложный

Соединение двух 5-симплексов в двойной конфигурации можно увидеть на этой плоской проекции Кокстера A6 с красными и синими 5-симплексными вершинами и краями. Это соединение имеет симметрию [[3,3,3,3]] порядка 1440. Пересечение этих двух 5-симплексов представляет собой однородный биректифицированный 5-симплекс . = ∩ .

Связанные однородные 5-многогранники

Это первый размерный ряд однородных многогранников и сот, выраженный Коксетером как 1 _3k ряд . Вырожденный 4-мерный случай существует как 3-сферная мозаика, тетраэдрический осоэдр .

1 _3k- мерные фигуры
Космос	Конечный				евклидов	гиперболический
н	4	5	6	7	8	9
Коксетер группа	А ₃ А ₁	A_А5	Д ₆	E ₇	${\tilde {E}}_{7}$ =E ₇⁺	${\bar {T}}_{8}$ =E ₇⁺⁺
Коксетер диаграмма
Симметрия	[3 ^−1,3,1]	[3 ^0,3,1]	[3 ^1,3,1]	[3 ^2,3,1]	[[3 ^3,3,1]]	[3 ^4,3,1]
Заказ	48	720	23,040	2,903,040	∞
График					-	-
Имя	1 _3,-1	1 ₃₀	1 ₃₁	1 ₃₂	1 ₃₃	1 ₃₄

Это первый размерный ряд однородных многогранников и сот, выраженный Коксетером как 3 _k1 ряд . Вырожденный 4-мерный случай существует как 3-сферная мозаика, тетраэдрический диэдр .

3 _k1 размерные фигурки
Космос	Конечный				евклидов	гиперболический
н	4	5	6	7	8	9
Коксетер группа	А ₃ А ₁	A_А5	Д ₆	E ₇	${\tilde {E}}_{7}$ =E ₇⁺	${\bar {T}}_{8}$ =E ₇⁺⁺
Коксетер диаграмма
Симметрия	[3 ^−1,3,1]	[3 ^0,3,1]	[[3 ^1,3,1]] = [4,3,3,3,3]	[3 ^2,3,1]	[3 ^3,3,1]	[3 ^4,3,1]
Заказ	48	720	46,080	2,903,040	∞
График					-	-
Имя	3 _1,-1	3 ₁₀	3 ₁₁	3 ₂₁	3 ₃₁	3 ₄₁

5-симплекс, как многогранник 2 ₂₀ , стоит первым в размерном ряду 2 _2k .

2 _2k фигур n размеров
Космос	Конечный			евклидов	гиперболический
н	4	5	6	7	8
Коксетер группа	А ₂ А ₂	A_А5	E_Е6	${\tilde {E}}_{6}$ = Е ₆⁺	E_Е6⁺⁺
Коксетер диаграмма
График				∞	∞
Имя	2 _2,-1	2 ₂₀	2 ₂₁	2 ₂₂	2 ₂₃

Правильный 5-симплекс — это один из 19 однородных политеров , основанных на группе [3,3,3,3] Кокстера , все они показаны здесь в _{A 5} плоскости Кокстера ортогональных проекциях . (Вершины окрашены в порядке перекрытия проекций: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый с увеличением количества вершин)

Многогранники А5
t₀	t₁	t₂	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_0,4	t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4
t_0,2,4	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,1,2,3,4

См. также

11-ячеечный

Примечания

^ Клитцинг, Ричард. «5D однородные многогранники (политеры) x3o3o3o3o — hix» .
^ Коксетер 1973 , §1.8 Конфигурации
^ Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. п. 117. ИСБН 9780521394901 .

Ссылки

Госсет, Т. (1900). «О правильных и полуправильных фигурах в пространстве n измерений». Вестник математики . Макмиллан. стр. 43–.
Коксетер, HSM :
- — (1973). «Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5)». Правильные многогранники (3-е изд.). Дувр. стр. 296 . ISBN 0-486-61480-8 .
- Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони К.; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные сочинения HSM Coxeter . Уайли. ISBN 978-0-471-01003-6 .
  - (Документ 22) — (1940). «Правильные и полуправильные многогранники I» . Математика. Зейт . 46 : 380–407. дои : 10.1007/BF01181449 . S2CID 186237114 .
  - (Документ 23) — (1985). «Правильные и полуправильные многогранники II» . Математика. Зейт . 188 (4): 559–591. дои : 10.1007/BF01161657 . S2CID 120429557 .
  - (Документ 24) — (1988). «Правильные и полуправильные многогранники III» . Математика. Зейт . 200 : 3–45. дои : 10.1007/BF01161745 . S2CID 186237142 .
Конвей, Джон Х .; Бургель, Хайди; Гудман-Штраус, Хаим (2008). «26. Гемикубы: 1 _n1 ». Симметрии вещей . п. 409. ИСБН 978-1-56881-220-5 .
Джонсон, Норман (1991). «Равномерные многогранники» (Рукопись). Норман Джонсон.
- Джонсон, Северо-Запад (1966). Теория однородных многогранников и сот (доктор философии). Университет Торонто.

Внешние ссылки

Ольшевский, Георгий. «Симплекс» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
Многогранники различных размерностей , Джонатан Бауэрс
Многомерный глоссарий

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Клитцинг, Ричард. «5D однородные многогранники (политеры) x3o3o3o3o — hix» .

[2] Коксетер 1973 , §1.8 Конфигурации

[3] Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. п. 117. ИСБН 9780521394901 .

[1]

[2]

[3]