Адиабатический процесс

Эта статья об адиабатических процессах в термодинамике. Чтобы узнать об адиабатической теореме в квантовой механике, см. Адиабатическая теорема .

Адиабатический процесс ( адиабатический от древнегреческого ἀδιάβατος ( adiábatos ) «непроходимый») — это тип термодинамического процесса. Это происходит без передачи тепла или массы между термодинамической системой и ее средой . В отличие от изотермического процесса , адиабатический процесс передает энергию окружающей среде только в виде работы . Как ключевое понятие термодинамики , адиабатический процесс поддерживает теорию, объясняющую первый закон термодинамики . Термин, противоположный термину «адиабатический», — «диабатический » .

Некоторые химические и физические процессы происходят слишком быстро, чтобы энергия могла войти в систему или выйти из нее в виде тепла, что позволяет использовать удобное «адиабатическое приближение». Например, адиабатическая температура пламени использует это приближение для расчета верхнего предела температуры пламени , предполагая, что при горении тепло не теряется в окружающую среду.

В метеорологии адиабатическое расширение и охлаждение влажного воздуха, которое может быть вызвано, например, ветрами, дующими вверх и над горами, может привести к тому, что давление водяного пара превысит давление насыщенного пара . Расширение и охлаждение сверх давления насыщенного пара часто идеализируются как псевдоадиабатический процесс , при котором избыточный пар мгновенно осаждается в капли воды. Изменение температуры воздуха, подвергающегося псевдоадиабатическому расширению, отличается от воздуха, подвергающегося адиабатическому расширению, поскольку скрытое тепло . в результате осадков выделяется

Описание

Процесс без передачи тепла в систему или из нее, так что Q = 0 , называется адиабатическим, а такая система называется адиабатически изолированной. Часто делается упрощающее предположение, что процесс является адиабатическим. Например, предполагается, что сжатие газа в цилиндре двигателя происходит настолько быстро, что во временном масштабе процесса сжатия незначительная часть энергии системы может быть передана в виде тепла в окружающую среду. Несмотря на то, что цилиндры не изолированы и являются достаточно проводящими, этот процесс идеализируется как адиабатический. То же самое можно сказать и о процессе расширения такой системы.

Предположение об адиабатической изоляции полезно и часто сочетается с другими подобными идеализациями для расчета хорошего первого приближения поведения системы. Например, по мнению Лапласа , при распространении звука в газе нет времени для теплопроводности в среде, и поэтому распространение звука является адиабатическим. Для такого адиабатического процесса модуль упругости ( модуль Юнга ) можно выразить как E = γP , где γ — отношение удельных теплоемкостей при постоянном давлении и постоянном объеме ( γ = ⁠ C _p / C _v ⁠ ) и P — давление газа.

Различные применения адиабатического предположения

Для закрытой системы первый закон термодинамики можно записать как Δ U = Q − W , где Δ U обозначает изменение внутренней энергии системы, Q - количество энергии, добавленной к ней в виде тепла, а W - работу, совершаемую система в своем окружении.

• Если система имеет такие жесткие стенки, что работа не может передаваться внутрь или наружу ( W = 0 ), и стенки не адиабатические и энергия добавляется в виде тепла ( Q > 0 ), и фазового перехода нет, то температура системы повысится.
• Если система имеет настолько жесткие стенки, что работа давление-объем не может быть совершена, но стенки адиабатические ( Q = 0 ), а энергия добавляется в виде изохорной (постоянного объема) работы в виде трения или перемешивания вязкой жидкости. внутри системы ( W < 0 ) и фазового перехода нет, то температура системы повысится.
• Если стенки системы адиабатические ( Q = 0 ), но не жесткие ( W ≠ 0 ), и в фиктивном идеализированном процессе энергия добавляется к системе в виде невязкой работы давление-объем без трения ( W < 0 ), а фазового перехода нет, то температура системы повысится. Такой процесс называется «обратимым». В идеале, если бы процесс был обращен вспять, энергия могла бы быть полностью восстановлена ​​как работа, совершенная системой. Если работу сложить так, что внутри системы действуют силы трения или вязкости, и если фазового перехода нет, то температура системы повысится, то процесс называется «необратимым», а работа добавленное в систему не полностью восстанавливается в рабочем виде.
• Если стенки системы неадиабатические и энергия передается в виде тепла, процесс не является адиабатическим, поскольку Q > 0 и Δ S > 0 согласно второму началу термодинамики .

Адиабатические процессы, происходящие в природе, необратимы.

Перенос энергии как работы в адиабатически изолированную систему можно представить как два крайних идеализированных вида. В одном таком виде нет трения, вязкой диссипации и т. д., а работа представляет собой только работу давление-объем (обозначается P d V ). В природе этот идеальный вид встречается лишь приблизительно, поскольку он требует бесконечно медленного процесса и отсутствия источников рассеяния.

Другой крайний вид работы — изохорная работа ( d V = 0 ), при которой энергия добавляется в виде работы исключительно за счет трения или вязкой диссипации внутри системы. Мешалка, передающая энергию вязкой жидкости адиабатически изолированной системы с жесткими стенками, без фазового перехода, вызовет повышение температуры жидкости, но эта работа невозвратима. Изохорная работа необратима. Второй закон термодинамики гласит, что естественный процесс передачи энергии как работы всегда состоит, по крайней мере, из изохорной работы, а часто и из обоих этих крайних видов работы. Каждый естественный процесс, адиабатический или нет, необратим при Δ S > 0 , поскольку в той или иной степени всегда присутствуют трение или вязкость.

Адиабатическое сжатие и расширение

Адиабатическое сжатие газа приводит к повышению температуры газа. Адиабатическое расширение под действием давления или пружины вызывает падение температуры. Напротив, свободное расширение — это изотермический процесс для идеального газа.

Адиабатическое сжатие происходит, когда давление газа увеличивается за счет работы, совершаемой над ним окружающей средой, например, поршень сжимает газ, содержащийся внутри цилиндра, и повышает температуру, тогда как во многих практических ситуациях теплопроводность через стенки может быть медленной по сравнению с время сжатия. Это находит практическое применение в дизельных двигателях , в которых отсутствие рассеивания тепла во время такта сжатия позволяет достаточно повысить температуру паров топлива для его воспламенения.

Адиабатическое сжатие происходит в атмосфере Земли , когда воздушная масса опускается, например, при катабатическом ветре , ветре Фена или ветре Чинук, стекающем вниз по горному хребту. Когда пакет воздуха опускается, давление на пакет увеличивается. Из-за этого увеличения давления объем пакета уменьшается, а его температура увеличивается по мере совершения работы над пакетом воздуха, увеличивая тем самым его внутреннюю энергию, которая проявляется в повышении температуры этой массы воздуха. Посылка воздуха может лишь медленно рассеивать энергию за счет проводимости или излучения (тепла), и в первом приближении ее можно считать адиабатически изолированной, а этот процесс - адиабатическим процессом.

Адиабатическое расширение происходит, когда давление на адиабатически изолированную систему уменьшается, позволяя ей расширяться в размерах, тем самым заставляя ее совершать работу над своим окружением. Когда давление, оказываемое на пакет газа, уменьшается, газ в пакете может расшириться; с увеличением объема температура падает, а его внутренняя энергия уменьшается. В атмосфере Земли происходит адиабатическое расширение с орографическим подъемом и подветренными волнами , что может привести к образованию пилей или линзовидных облаков .

Частично из-за адиабатического расширения в горных районах снегопады в некоторых частях пустыни Сахара случаются нечасто .

Адиабатическое расширение не обязательно должно включать жидкость. Одним из методов, используемых для достижения очень низких температур (тысячные и даже миллионные доли градуса выше абсолютного нуля), является адиабатическое размагничивание , при котором изменение магнитного поля на магнитном материале используется для обеспечения адиабатического расширения. Кроме того, содержимое расширяющейся Вселенной можно описать (в первом порядке) как адиабатически расширяющуюся жидкость. (См. Тепловая смерть Вселенной .)

Поднимающаяся магма также подвергается адиабатическому расширению перед извержением, что особенно важно в случае магм, которые быстро поднимаются с больших глубин, таких как кимберлиты .

В конвективной мантии Земли (астеносфере) под литосферой температура мантии составляет примерно адиабату. Небольшое снижение температуры с уменьшением глубины связано с уменьшением давления по мере того, как мельче находится материал в Земле.

Такие изменения температуры можно определить количественно, используя закон идеального газа или уравнение гидростатики для атмосферных процессов.

На практике ни один процесс не является истинно адиабатическим. Многие процессы основаны на большой разнице во временных масштабах интересующего процесса и скорости рассеяния тепла через границу системы и, таким образом, аппроксимируются с использованием адиабатического предположения. Всегда есть некоторая потеря тепла, поскольку идеальных изоляторов не существует.

Идеальный газ (обратимый процесс)

Основная статья: Обратимый адиабатический процесс

Для простого вещества при адиабатическом процессе увеличения объема внутренняя энергия рабочего вещества должна уменьшаться.

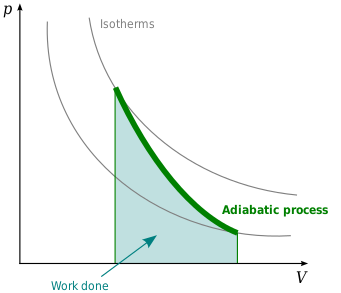
Математическое уравнение идеального газа, претерпевающего обратимый адиабатический процесс, можно представить политропного процесса. уравнением

$PV^{\gamma }={\text{constant}},$

где P — давление, V — объем, а γ — показатель адиабаты или коэффициент теплоемкости, определяемый как

$\gamma ={\frac {C_{P}}{C_{V}}}={\frac {f+2}{f}}.$

Здесь C _P — удельная теплоемкость при постоянном давлении, C _V — удельная теплоемкость при постоянном объеме, а f — число степеней свободы (3 для одноатомного газа, 5 для двухатомного газа или газа с линейными молекулами, например углекислый газ).

Для одноатомного идеального газа γ = ⁠ 5/3 азота ⁠ , а для двухатомного газа (например, и кислорода , основных компонентов воздуха) γ = ⁠ 7 / 5 ⁠ . Обратите внимание, что приведенная выше формула применима только к классическим идеальным газам (то есть газам, температура которых намного выше абсолютного нуля), а не к Бозе-Эйнштейна или газам Ферми .

Можно также использовать закон идеального газа, чтобы переписать приведенную выше связь между P и V как

$P^{1-\gamma }T^{\gamma }={\text{constant}},$

$TV^{\gamma -1}={\text{constant}}.$

где Т — абсолютная или термодинамическая температура .

Пример адиабатического сжатия

Такт сжатия в бензиновом двигателе можно использовать как пример адиабатического сжатия. Допущения модели таковы: несжатый объем цилиндра составляет один литр (1 л = 1000 см3). ³ = 0,001 м ³ ); газ внутри — это воздух, состоящий только из молекулярного азота и кислорода (таким образом, двухатомный газ с 5 степенями свободы, и поэтому γ = ⁠ 7/5 ​ ⁠ ) ; степень сжатия двигателя 10:1 (т.е. объем 1 л несжатого газа уменьшается поршнем до 0,1 л); а несжатый газ имеет примерно комнатную температуру и давление (теплая комнатная температура ~ 27 ° C или 300 К и давление 1 бар = 100 кПа, т.е. типичное атмосферное давление на уровне моря).

${\begin{aligned}&P_{1}V_{1}^{\gamma }=\mathrm {constant} _{1}=100\,000~{\text{Pa}}\times (0.001~{\text{m}}^{3})^{\frac {7}{5}}\\&=10^{5}\times 6.31\times 10^{-5}~{\text{Pa}}\,{\text{m}}^{21/5}=6.31~{\text{Pa}}\,{\text{m}}^{21/5},\end{aligned}}$

поэтому адиабатическая константа для этого примера составляет около 6,31 Па·м. ^4.2 .

Теперь газ сжимается до 0,1 л (0,0001 м3). ³ ) объема, который, как мы предполагаем, происходит достаточно быстро, чтобы тепло не проникало в газ и не покидало его через стенки. Адиабатическая константа остается прежней, но результирующее давление неизвестно.

$P_{2}V_{2}^{\gamma }=\mathrm {constant} _{1}=6.31~{\text{Pa}}\,{\text{m}}^{21/5}=P\times (0.0001~{\text{m}}^{3})^{\frac {7}{5}},$

Теперь мы можем определить конечное давление.

$P_{2}=P_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }=100\,000~{\text{Pa}}\times {\text{10}}^{7/5}=2.51\times 10^{6}~{\text{Pa}}$

или 25,1 бар. Это увеличение давления превышает простую степень сжатия 10: 1; это связано с тем, что газ не только сжимается, но работа, совершаемая по сжатию газа, увеличивает и его внутреннюю энергию, что проявляется в повышении температуры газа и дополнительном повышении давления сверх того, что получилось бы при упрощенном расчете 10 раз превышает исходное давление.

Мы также можем определить температуру сжатого газа в цилиндре двигателя, используя закон идеального газа PV = nRT ( n — количество газа в молях, а R — газовая постоянная для этого газа). Наши начальные условия: давление 100 кПа, объем 1 л и температура 300 К, наша экспериментальная константа ( nR ) равна:

${\frac {PV}{T}}=\mathrm {constant} _{2}={\frac {10^{5}~{\text{Pa}}\times 10^{-3}~{\text{m}}^{3}}{300~{\text{K}}}}=0.333~{\text{Pa}}\,{\text{m}}^{3}{\text{K}}^{-1}.$

Мы знаем, что сжатый газ имеет V = 0,1 л и P = 2,51 × 10. ⁶ Pa , поэтому мы можем найти температуру:

$T={\frac {PV}{\mathrm {constant} _{2}}}={\frac {2.51\times 10^{6}~{\text{Pa}}\times 10^{-4}~{\text{m}}^{3}}{0.333~{\text{Pa}}\,{\text{m}}^{3}{\text{K}}^{-1}}}=753~{\text{K}}.$

Это конечная температура 753 К, или 479 °С, или 896 °F, что значительно выше точки воспламенения многих видов топлива. Вот почему для двигателя с высокой степенью сжатия требуется топливо, специально разработанное для предотвращения самовоспламенения (что могло бы вызвать детонацию двигателя при работе в таких условиях температуры и давления), или чтобы нагнетатель с промежуточным охладителем обеспечивал наддув давления, но с более низким давлением. Повышение температуры будет преимуществом. Дизельный двигатель работает в еще более экстремальных условиях, обычно со степенью сжатия 16:1 или более, чтобы обеспечить очень высокое давление газа, обеспечивающее немедленное воспламенение впрыскиваемого топлива.

Адиабатическое свободное расширение газа

См. также: Бесплатное расширение.

При адиабатическом свободном расширении идеального газа газ содержится в изолированном контейнере, а затем ему позволяют расширяться в вакууме. Поскольку нет внешнего давления, против которого газ мог бы расшириться, работа, совершаемая системой или над ней, равна нулю. Поскольку этот процесс не предполагает какой-либо теплопередачи или работы, первый закон термодинамики предполагает, что чистое изменение внутренней энергии системы равно нулю. Для идеального газа температура остается постоянной, поскольку в этом случае внутренняя энергия зависит только от температуры. Этот процесс необратим.

Вывод зависимости P – V для адиабатического сжатия и расширения.

Определение адиабатического процесса состоит в том, что передача тепла в систему равна нулю, δQ = 0 . Тогда, согласно первому закону термодинамики,

$dU+\delta W=\delta Q=0,$ ( а1 )

где dU — изменение внутренней энергии системы, а δW — работа, совершаемая системой . Любая работа ( δW ) должна быть выполнена за счет внутренней энергии U , поскольку тепло δQ не поступает из окружающей среды. Работа давление-объем δW, совершаемая системой , определяется как

$\delta W=P\,dV.$ ( а2 )

Однако P не остается постоянным во время адиабатического процесса, а изменяется вместе V. с

Желательно знать, как значения dP и dV соотносятся друг с другом при протекании адиабатического процесса. Для идеального газа (вспомним закон идеального газа PV = nRT ) внутренняя энергия определяется выражением

$U=\alpha nRT=\alpha PV,$ ( а3 )

где α — число степеней свободы, деленное на 2, R — универсальная газовая постоянная , а n — количество молей в системе (константа).

Дифференцирующее уравнение (a3) ​​дает

$dU=\alpha nR\,dT=\alpha \,d(PV)=\alpha (P\,dV+V\,dP).$ ( a4 )

Уравнение (a4) часто выражается как dU = nC _V dT, поскольку C _V = αR .

Теперь подставим уравнения (a2) и (a4) в уравнение (a1), чтобы получить

$-P\,dV=\alpha P\,dV+\alpha V\,dP,$

факторизовать − P dV :

$-(\alpha +1)P\,dV=\alpha V\,dP,$

и разделим обе части на PV :

$-(\alpha +1){\frac {dV}{V}}=\alpha {\frac {dP}{P}}.$

После интегрирования левой и правой частей от V ₀ до V и от P ₀ до P и изменения сторон соответственно,

$\ln \left({\frac {P}{P_{0}}}\right)=-{\frac {\alpha +1}{\alpha }}\ln \left({\frac {V}{V_{0}}}\right).$

Возвести в степень обе стороны, заменить ⁠ α + 1 / α ⁠ с γ , коэффициент теплоемкости

$\left({\frac {P}{P_{0}}}\right)=\left({\frac {V}{V_{0}}}\right)^{-\gamma },$

и устраним отрицательный знак, чтобы получить

$\left({\frac {P}{P_{0}}}\right)=\left({\frac {V_{0}}{V}}\right)^{\gamma }.$

Поэтому,

$\left({\frac {P}{P_{0}}}\right)\left({\frac {V}{V_{0}}}\right)^{\gamma }=1,$

и

$P_{0}V_{0}^{\gamma }=PV^{\gamma }=\mathrm {constant} .$

$\Delta U=\alpha RnT_{2}-\alpha RnT_{1}=\alpha Rn\Delta T.$ ( б1 )

В то же время работа, совершаемая изменением давления-объема в результате этого процесса, равна

$W=\int _{V_{1}}^{V_{2}}P\,dV.$ ( б2 )

Поскольку мы требуем, чтобы процесс был адиабатическим, следующее уравнение должно быть верным

$\Delta U+W=0.$ ( б3 )

Согласно предыдущему выводу,

$PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.$ ( б4 )

Перестановка (b4) дает

$P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.$

Подстановка этого в (b2) дает

$W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\,dV.$

Интегрируя, получим выражение для работы:

$W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.$

Подставив γ = ⁠ α + 1 / α ⁠ во втором члене,

$W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma }-V_{1}^{1-\gamma }\right).$

Перестановка,

$W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).$

Используя закон идеального газа и предполагая постоянное молярное количество (как это часто бывает в практических случаях),

$W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).$

По непрерывной формуле

${\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1}}}\right)^{-\gamma },$

или

$\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}}{V_{1}}}.$

Подставив в предыдущее выражение W ,

$W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).$

Подстановка этого выражения и (b1) в (b3) дает

$\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).$

Упрощая,

$T_{2}-T_{1}=T_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),$

${\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1,$

$T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.$

Вывод дискретной формулы и рабочего выражения

Изменение внутренней энергии системы, измеренное от состояния 1 к состоянию 2, равно

В то же время работа, совершаемая изменением давления-объема в результате этого процесса, равна

$W=\int _{V_{1}}^{V_{2}}P\,dV.$ ( с2 )

Поскольку мы требуем, чтобы процесс был адиабатическим, следующее уравнение должно быть верным

$\Delta U+W=0.$ ( с3 )

Согласно предыдущему выводу,

$PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.$ ( с4 )

Перестановка (c4) дает

$P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.$

Подстановка этого в (c2) дает

$W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\,dV.$

Интегрируя, получим выражение для работы:

$W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.$

Подставив γ = ⁠ α + 1 / α ⁠ во втором члене,

$W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma }-V_{1}^{1-\gamma }\right).$

Перестановка,

$W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).$

Используя закон идеального газа и предполагая постоянное молярное количество (как это часто бывает в практических случаях),

$W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).$

По непрерывной формуле

${\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1}}}\right)^{-\gamma },$

или

$\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}}{V_{1}}}.$

Подставив в предыдущее выражение W ,

$W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).$

Подстановка этого выражения и (c1) в (c3) дает

$\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right).$

Упрощая,

$T_{2}-T_{1}=T_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),$

${\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1,$

$T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.$

Этимология

Термин адиабатический ( / ˌ æ d i ə ˈ b æ t ɪ k / ) представляет собой англизированную версию греческого термина ἀδιάβατος «непроходимый» (использованный Ксенофонтом о реках). В термодинамическом смысле он используется Рэнкином (1866), и принят Максвеллом в 1871 году (явно приписывая этот термин Рэнкину). Этимологическое происхождение здесь соответствует невозможности передачи энергии в виде тепла и переноса материи через стену.

Греческое слово ἀδιάβατος образовано от приватного ἀ- («не») и διαβατός, «проходимый», в свою очередь происходящего от διά («сквозь») и βαῖνειν («идти, идти, приходить»).

Концептуальное значение в термодинамической теории

Адиабатический процесс был важен для термодинамики с первых дней ее существования. Это было важно в работах Джоуля , поскольку давало возможность почти напрямую связать количества тепла и работы.

Энергия может входить или выходить из термодинамической системы, окруженной стенками, препятствующими массопереносу , только в виде тепла или работы. Следовательно, количество работы в такой системе может быть почти напрямую связано с эквивалентным количеством тепла в цикле двух конечностей. системы Первая часть представляет собой изохорный адиабатический рабочий процесс, увеличивающий внутреннюю энергию ; второй — изохорный и безработный теплообмен, возвращающий систему в исходное состояние. Соответственно, Рэнкин измерял количество теплоты в единицах работы, а не как калориметрическую величину. В 1854 году Рэнкин использовал величину, которую он назвал «термодинамической функцией», которая позже была названа энтропией, и в то же время он написал также о «кривой отсутствия передачи тепла». которую он позже назвал адиабатической кривой. Помимо двух изотермических участков, цикл Карно имеет два адиабатических участка.

Концептуальную важность этого для основ термодинамики подчеркнул Брайан: Каратеодори, и Борн. Причина в том, что калориметрия предполагает тип температуры, который уже был определен до формулировки первого закона термодинамики, например, основанный на эмпирических шкалах. Такое предположение предполагает проведение различия между эмпирической температурой и абсолютной температурой. Скорее, определение абсолютной термодинамической температуры лучше оставить до тех пор, пока второй закон не станет концептуальной основой.

В восемнадцатом веке закон сохранения энергии еще не был полностью сформулирован и установлен, и природа тепла дискутировалась. Один из подходов к решению этих проблем заключался в том, чтобы рассматривать тепло, измеряемое калориметрически, как первичное вещество, сохраняющееся в количестве. К середине девятнадцатого века она была признана формой энергии, и тем самым был также признан закон сохранения энергии. Мнение, которое со временем утвердилось и в настоящее время считается правильным, состоит в том, что закон сохранения энергии является основной аксиомой, и что тепло следует анализировать как вытекающее из него. В этом свете тепло не может быть компонентом полной энергии отдельного тела, потому что это не переменная состояния , а, скорее, переменная, описывающая передачу между двумя телами. Адиабатический процесс важен, потому что он является логическим компонентом современной точки зрения.

Различные варианты использования слова адиабатический.

Настоящая статья написана с точки зрения макроскопической термодинамики, и слово адиабатический используется в этой статье в традиционном понимании термодинамики, введенном Рэнкином. В настоящей статье указывается, что, например, если сжатие газа происходит быстро, то времени для теплопередачи остается мало, даже если газ не изолирован адиабатически определенной стенкой. В этом смысле быстрое сжатие газа иногда приблизительно или условно называют адиабатическим , даже если газ не изолирован адиабатически определенной стенкой.

Некоторые авторы, например Пиппард , рекомендуют использовать термин «адиатермический» для обозначения процессов, в которых не происходит теплообмена (например, джоулево расширение), а термин «адиабатический» — для обратимых квазистатических адиатермических процессов (так что быстрое сжатие газа не происходит ) . адиабатический»). А Лайдлер обобщил сложную этимологию слова «адиабатический».

Однако квантовая механика и квантовая статистическая механика используют слово «адиабатический» в совершенно другом смысле , который иногда может показаться почти противоположным классическому термодинамическому смыслу. В квантовой теории слово адиабатический может означать что-то близкое к квазистатическому , но использование этого слова в двух дисциплинах сильно различается.

С одной стороны, в квантовой теории, если пертурбативный элемент работы сжатия выполняется почти бесконечно медленно (то есть квазистатически), говорят, что он был выполнен адиабатически . Идея состоит в том, что формы собственных функций изменяются медленно и непрерывно, так что квантовый скачок не срабатывает, и изменение практически обратимо. Хотя числа заполнения не изменились, тем не менее, происходят изменения в энергетических уровнях взаимно однозначных соответствующих собственных состояний до и после сжатия. Таким образом, пертурбативный элемент работы был выполнен без теплопередачи и без внесения случайных изменений в систему. Например, Макс Борн пишет: «На самом деле обычно нам приходится иметь дело с «адиабатическим» случаем: т. е. предельным случаем, когда внешняя сила (или реакция частей системы друг на друга) действует очень медленно. В этом случае в очень высоком приближении

$c_{1}^{2}=1,\,\,c_{2}^{2}=0,\,\,c_{3}^{2}=0,\,...\,,$

т. е. вероятность перехода отсутствует и система после прекращения возмущения находится в исходном состоянии. Следовательно, такое медленное возмущение обратимо, как и в классическом случае».

С другой стороны, в квантовой теории, если пертурбативный элемент работы сжатия совершается быстро, он изменяет числа заполнения и энергии собственных состояний пропорционально интегралу момента перехода и в соответствии с зависящей от времени теорией возмущений , а также нарушая функциональную форму самих собственных состояний. В этой теории такое быстрое изменение называется не адиабатическим противоположное слово «диабатический» , и к нему применяется .

Недавние исследования предполагает, что мощность, поглощаемая возмущением, соответствует скорости этих неадиабатических переходов. Это соответствует классическому процессу передачи энергии в виде тепла, но с обратными относительными временными масштабами в квантовом случае. Квантовые адиабатические процессы происходят в относительно длительных временных масштабах, тогда как классические адиабатические процессы происходят в относительно коротких временных масштабах. Следует также отметить, что концепция «тепла» (в отношении количества передаваемой тепловой энергии ) не работает на квантовом уровне, и вместо этого необходимо учитывать конкретную форму энергии (обычно электромагнитную). Небольшое или незначительное поглощение энергии от возмущения в квантовом адиабатическом процессе дает хорошее основание для идентификации его как квантового аналога адиабатических процессов в классической термодинамике и для повторного использования этого термина.

Более того, в атмосферной термодинамике диабатический процесс — это процесс теплообмена.

В классической термодинамике такое быстрое изменение все равно назвали бы адиабатическим, поскольку система адиабатически изолирована и передача энергии в виде тепла отсутствует. Сильная необратимость изменений из-за вязкости не мешает этому классическому использованию.

Таким образом, для массы газа в макроскопической термодинамике используются такие слова, что сжатие иногда условно или приблизительно называют адиабатическим, если оно достаточно быстрое, чтобы избежать значительной передачи тепла, даже если система не адиабатически изолирована. Но в квантовой статистической теории сжатие не называется адиабатическим, если оно происходит быстро, даже если система адиабатически изолирована в классическом термодинамическом смысле этого слова. Как указано выше, в двух дисциплинах эти слова используются по-разному.

См. также

• Пожарный поршень
• Тепловой взрыв

Связанные темы по физике

• Первый закон термодинамики
• Адиабатическая проводимость
• Адиабатический градиент скорости
• Общая температура воздуха
• Магнитное охлаждение
• Ягодная фаза

Связанные термодинамические процессы

• Циклический процесс
• Изобарный процесс
• Изентальпический процесс
• Изохорный процесс
• Изотермический процесс
• Политропный процесс
• Квазистатический процесс

Ссылки

Общий

• Силби, Роберт Дж.; и др. (2004). Физическая химия . Хобокен, Нью-Джерси: Уайли. п. 55. ИСБН  978-0-471-21504-2 .
• Нейв, Карл Род. « Адиабатические процессы ». Гиперфизика.
• Торнгрен, доктор Джейн Р. « Адиабатические процессы ». Дафна - веб-сервер колледжа Паломар, 21 июля 1995 г. Архивировано 9 мая 2011 г. на Wayback Machine .

Внешние ссылки

СМИ, связанные с адиабатическими процессами, на Викискладе?

• Статья в энциклопедии гиперфизики