Срезной узел

Гладкий срез диска в позиции Морзе , показывающий минимумы, седла и максимумы, а также в качестве иллюстрации фильм об узле Киношита-Терасака.

Узел среза — это математический узел в трехмерном пространстве, ограничивающий вложенный диск в четырехмерном пространстве.

Определение

Узел $K\subset S^{3}$ называется топологически срезным узлом или гладко срезным узлом , если он является границей вложенного диска в 4-шар. $B^{4}$, который является локально плоским или гладким соответственно. Здесь мы используем $S^{3}=\partial B^{4}$: 3-сфера $S^{3}=\{\mathbf {x} \in \mathbb {R} ^{4}:|\mathbf {x} |=1\}$ — граница четырёхмерного шара $B^{4}=\{\mathbf {x} \in \mathbb {R} ^{4}:|\mathbf {x} |\leq 1\}.$ Каждый гладко срезанный узел топологически является срезом, поскольку гладко вложенный диск локально плоский. Обычно гладко срезанные узлы еще называют просто срезными. Оба типа узлов срезов важны в трехмерной и четырехмерной топологии.

Узлы с гладкими срезами часто иллюстрируются с использованием диаграмм ленточных узлов , и остается открытым вопрос, существуют ли какие-либо узлы с гладкими срезами, которые не являются ленточными узлами («Гипотеза о срезе ленты»).

Конусная конструкция

Конус над узлом трилистника

В определении существенны условия локально-плоской или гладкости: для каждого узла можно построить конус над узлом, который является диском в 4-шаре с требуемым свойством, за исключением того, что он не является локально-плоским или гладким в точке сингулярность (хотя это работает и для тривиального узла).

Обратите внимание, что диск на рисунке справа не имеет самопересечений в 4-мерном пространстве. Они происходят только в проекции на трехмерное пространство. Следовательно, диск «правильно» вложен в каждой точке, но не в особенности (он там не локально-плоский).

Узлы срезов и группа согласования узлов

Два ориентированных узла $K_{1},K_{2}$ называются согласованными , если связная сумма $K_{1}\sharp -K_{2}$ это кусочек. Так же, как и раньше, выделим топологически и гладко согласованные. С $-K_{2}$ мы обозначаем зеркальное отображение $K_{2}$ где, кроме того, ориентация меняется на противоположную. Отношение «согласованное» является рефлексивным, поскольку $K\sharp -K$ это кусочек для каждого узла $K$. Можно также показать, что оно транзитивно: если $K_{1}$ соответствует $K_{2}$ и $K_{2}$ соответствует $K_{3}$ затем $K_{1}$ соответствует $K_{3}$. Поскольку отношение также симметрично, оно является отношением эквивалентности . Классы эквивалентности вместе со связной суммой узлов в качестве операции тогда образуют абелеву группу , которая называется (топологической или гладкой) группой согласия узлов. Нейтральным элементом в этой группе является множество узлов срезов (топологических или гладких соответственно).

Примеры

С помощью узла-трилистника мы иллюстрируем рефлексивность отношения согласования: каждый узел согласен сам с собой. При определении согласованности происходят две смены ориентаций: меняется ориентация узла (зеленая и красная стрелки), а также ориентация трехмерного пространства. Эффект последнего – зеркальное отображение узла.

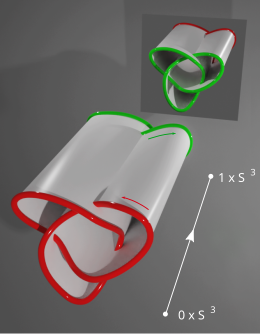
Каждый ленточный узел является узлом с гладкими срезами, потому что, за исключением особенностей ленты, узел уже ограничивает вложенный диск (в трехмерном пространстве). Ленточные особенности могут быть в небольшой окрестности деформированы в 4-мерное пространство так, что диск будет вложен.

Существует 21 нетривиальный срезный простой узел с числом пересечений. $cr(K)\leq 10$. Это $6_{1}$, $8_{8}$, $8_{9}$, $8_{20}$, $9_{27}$, $9_{41}$, $9_{46}$, $10_{3}$, $10_{22}$, $10_{35}$, $10_{42}$, $10_{48}$, $10_{75}$, $10_{87}$, $10_{99}$, $10_{123}$, $10_{129}$, $10_{137}$, $10_{140}$, $10_{153}$ и $10_{155}$. До этого числа пересечений не существует топологически срезанных узлов, которые не были бы гладко срезанными. Однако, начиная с пересечения номер 11, есть такой пример: узел Конвея (названный в честь Джона Хортона Конвея ) топологически, но не гладко разрезаемый узел. С другой стороны, узел Киношита-Терасака, так называемый « мутант » узла Конвея, плавно разрезается. Крученые узлы , кроме тривиального узла и стивидорного узла. $6_{1}$, а не ломтик. Все топологически и плавно нарезанные узлы с номером пересечения $cr(K)\leq 12$ известны. Сложные срезные узлы до номера пересечения 12 бывают, кроме узлов вида $K\sharp -K$ и $6_{1}\sharp 3_{1}\sharp -3_{1}$, еще два интересных узла $3_{1}\sharp 8_{10}$ и $3_{1}\sharp 8_{11}$.

Инварианты

Для топологически и гладко срезанных узлов справедливы следующие свойства:Полином Александера срезного узла можно записать как $\Delta (t)=f(t)f(t^{-1})$ с полиномом Лорана $f$ с целыми коэффициентами (условие Фокса-Милнора). Отсюда следует, что определитель узла ( $=\Delta (-1)$) — квадратное число.

Сигнатура является инвариантом классов согласования, а сигнатура узлов срезов равна нулю. Более того, карта сигнатур представляет собой гомоморфизм группы согласования целых чисел : Подпись суммы двух классов согласования представляет собой сумму двух сигнатур.

• Отсюда следует, что группа согласования содержит элементы бесконечного порядка : сигнатура узла-трилистника равна ±2, а сигнатура класса согласования связной суммы $n$ трилистники это $\pm 2n$ и поэтому не 0.
• Группа согласования также содержит элементы 2-го порядка: Узел восьмерка. $4_{1}$ амфихейрально обратимо и имеем , поэтому мы $4_{1}=-4_{1}$. В группе согласования находим $4_{1}\sharp 4_{1}=4_{1}\sharp -4_{1}=0$. Поскольку определитель узла восьмерки равен 5, что не является квадратным числом, этот узел не является срезом, и отсюда следует, что его порядок в группе согласия равен 2. Конечно, узлы с конечным порядком в группе согласия всегда иметь подпись 0.

Для обоих вариантов группы согласия неизвестно, присутствуют ли элементы конечного порядка. $>2$ существовать.

С другой стороны, существуют инварианты с разными свойствами для двух вариантов согласования:Узлы с тривиальным полиномом Александера ( $\Delta (t)=1$) всегда топологически являются срезами, но не обязательно гладко срезами (примером является узел Конвея). S-инвариант Расмуссена исчезает для узлов с гладким срезом, но, вообще говоря, не для узлов с топологическим срезом.

Геометрическое описание отношения согласования

Вверху: композиция двух узловых согласований демонстрирует транзитивность геометрическим образом. Внизу: соответствие рода 1 между двумя узлами. Если узел слева тривиален, то узел справа имеет гладкий 4-род 0 или 1 — это граница вложенной поверхности рода 1, но он также может ограничивать диск.

В качестве альтернативы приведенному выше определению согласованности с использованием узлов срезов существует также второе эквивалентное определение. Два ориентированных узла $K_{1}$ и $K_{2}$ согласованы, если они являются границей (локально плоского или гладкого) цилиндра. $C=S^{1}\times [0,1]$ (в 4-мерном пространстве $S^{3}\times [0,1]$). Ориентация двух узлов должна совпадать с ориентацией цилиндра, как показано на третьем рисунке. Граница $S^{3}\times [0,1]$ два $S^{3}$ с разной ориентацией поэтому два зеркальных трилистника показаны как граница цилиндра. Соединение двух узлов путем вырезания полосы из цилиндра дает диск, показывая, что для всех узлов связная сумма $K\sharp -K$ это кусочек. В обоих определениях узел является срезом тогда и только тогда, когда он согласен с тривиальным узлом.

Это также можно проиллюстрировать с помощью первого рисунка вверху статьи: Если вырезать небольшой диск в локальном минимуме слева внизу, то граница поверхности в этом месте представляет собой тривиальный узел, а поверхность представляет собой цилиндр. . На другом конце цилиндра у нас имеется срезной узел. Если диск (или цилиндр) вставлен гладко, его можно слегка деформировать до так называемой позиции Морзе .

Это полезно, поскольку критические точки относительно радиальной функции r имеют геометрический смысл. В седловых точках тривиальные компоненты добавляются или уничтожаются (движения зон, также называемые слиянием и делением). Для ломтиковых узлов возможно любое количество таких перемещений полос, тогда как для ленточных узлов может происходить только слияние, а деление не допускается.

На рисунке справа геометрическое описание конкорданса повернуто на 90°, а параметр r переименован в t. Это название хорошо подходит для временной интерпретации поверхностного «кино».

4-род

Аналогичное определение узлов-срезов можно дать и для поверхностей большего рода . Таким образом, 4 -род (также называемый «родом срезов») узла определяется как наименьший род вложенной поверхности в 4-пространстве, границей которого является узел. Как и ранее, мы различаем топологический и гладкий 4-род. Узлы с 4-родом 0 являются срезными узлами, поскольку диск, простейшая поверхность, имеет род 0. 4-род всегда меньше или равен роду узла, поскольку этот инвариант определяется с использованием поверхностей Зейферта, которые уже встроены в трехмерные космос.

Примеры узлов с разными значениями топологического и гладкого 4-рода приведены в следующей таблице. Узел Конвея 11n34, как уже упоминалось, является первым примером в таблицах узлов топологически, но не гладко разрезаемого узла. Судя по значениям в таблице, можно заключить, что гладкий и топологический 4-род всегда отличаются на 1, если они не равны. Однако это не так, и разница может быть сколь угодно большой. Однако неизвестно (по состоянию на 2017 г.), существуют ли чередующиеся узлы с разницей > 1.

	$10_{139}$	$10_{145}$	$10_{152}$	$10_{154}$	$10_{161}$	$11n34$
4-род (гладкий)	4	2	4	3	3	1
4-род (верх.)	3	1	3	2	2	0

Библиография

• Дейл Рольфсен: Узлы и связи , Опубликуй или погибни, 1976, Глава 8.E
• Чарльз Ливингстон: Теория узлов , Математические монографии Каруса, 1993 г.
• Чарльз Ливингстон: Обзор классического соответствия узлов , глава 7 в «Справочнике по теории узлов», Elsevier, 2005 г.

Внешние ссылки

• Питер Тейхнер : Срезные узлы: теория узлов в 4-м измерении

См. также

• Согласование связей - отношение эквивалентности связей слабее, чем изотопия, но сильнее, чем гомотопия.