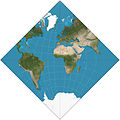
Многогранная картографическая проекция

Многогранная картографическая проекция — это картографическая проекция, основанная на сферическом многограннике . Обычно многогранник накладывается на глобус, и каждая грань многогранника преобразуется в многоугольник или другую форму на плоскости. Самая известная многогранная картографическая проекция — это Бакминстера Фуллера карта Dymaxion . Когда сферические грани многогранника преобразуются в грани обычного многогранника, а не лежат ровно на плоскости, в результате получается многогранный глобус . [1]
Часто используемый многогранник представляет собой Платоново тело или Архимедово тело . Однако можно использовать и другие многогранники: проекция AuthaGraph использует многогранник с 96 гранями, а многогранная проекция допускает произвольно большое количество граней. [2] Хотя прерывания между гранями являются обычным явлением и чаще встречаются с увеличением количества граней, на некоторых картах их избегают: конформная проекция Ли имеет прерывания только на границе, а проекция AuthaGraph масштабирует свои грани так, что карта заполняет прямоугольник без внутренних прерываний. . Некоторые проекции могут быть мозаичными , чтобы заполнить плоскость, в том числе конформная проекция Ли.
В некоторой степени многогранник и проекцию, используемую для преобразования каждой грани многогранника, можно рассматривать отдельно, а некоторые проекции можно применять к граням различной формы. Гномоническая проекция преобразует края сферических многогранников в прямые линии, сохраняя все многогранники, содержащиеся в полусфере, поэтому это распространенный выбор. можно Равновеликую проекцию Снайдера применить к любому многограннику с правильными гранями. [3] Проекцию, используемую в более поздних версиях карты Dymaxion, можно обобщить на другие равносторонние треугольные грани: [4] и даже к некоторым четырехугольникам. [5]
Многогранные картографические проекции полезны для создания дискретных глобальных сеток , например, четырехстороннего сферического куба и икосаэдральных сеток равной площади Снайдера (ISEA). [6]
История
[ редактировать ]Самая ранняя известная многогранная проекция — это октантная проекция, разработанная Леонардо да Винчи или его соратником около 1514 года, которая преобразует грани октаэдра в треугольники Рело . [1]
Кристиан Готлиб Райхард создал многогранный глобус на основе куба в 1803 году. Икосаэдрический глобус появился в 1851 году. Многогранные глобусы, дешево изготовленные из картона, какое-то время были популярны в Европе. [1]
Проекции, основанные на двугранниках, начали появляться с квинкунциальной проекцией Пирса в 1879 году, проекцией полусферы в квадрате Гую в 1887 году и проекцией полусферы в квадрате Адамса в 1925 году. Хотя диэдры не являются традиционными многогранниками, они представляют собой сферические многогранники. , а методы, используемые в этих проекциях, используются и в других многогранных проекциях. В той же работе, что и проекция «полушарие в квадрате», Адамс создал карты, изображающие весь земной шар в ромбе , шестиугольнике и гексаграмме . [7] [8]
Бернард Дж. С. Кэхилл изобрел «карту бабочки», основанную на октаэдре, в 1909 году. Она была обобщена в проекцию Кэхилла – Киз в 1975 году и проекцию бабочки Уотермана в 1996 году. Работа Кэхилла также оказала влияние на карты Dymaxion Фуллера: первую версию Фуллера. , основанный на кубооктаэдре , был опубликован в 1943 году, а его второй, основанный на икосаэдре, опубликован в 1954 году. [1]
В 1965 году Уэллман Чемберлин (также известный своей триметрической проекцией Чемберлина ) и Говард Э. Пейн из Национального географического общества разработали многогранную карту, основанную на 12 равных пятиугольных гранях додекаэдра . 20 лет спустя Чемберлин и Пейн использовали эту многогранную карту в «Global Pursuit», настольной игре, предназначенной для обучения детей географии. [9] [10]
Четырехсторонний сферический куб был разработан в 1975 году для проекта Cosmic Background Explorer . [11] [12]
Галерея
[ редактировать ]См. также
[ редактировать ]- HEALPix , который не является строго многогранной картографической проекцией.
- Список картографических проекций
Ссылки
[ редактировать ]- ^ Jump up to: а б с д Пенджих, Павел (01 декабря 2016 г.). «Образ Мира на многогранных картах и глобусах» . Польское картографическое обозрение . 48 (4): 197–210. дои : 10.1515/pcr-2016-0014 . ISSN 2450-6966 . S2CID 133013421 .
- ^ ван Вейк, Ярке Дж. (2008). «Развертывание Земли: Мириаэдрические проекции» . Картографический журнал . 45 (1): 32–42. дои : 10.1179/000870408X276594 . ISSN 0008-7041 . S2CID 218692689 .
- ^ Снайдер, Джон П. (1 марта 1992 г.). «Равновеликая картографическая проекция многогранных глобусов» . Cartographica: Международный журнал географической информации и геовизуализации . 29 (1): 10–21. дои : 10.3138/27H7-8K88-4882-1752 . ISSN 0317-7173 .
- ^ Крайдер, Джон Э. (01 марта 2008 г.). «Точные уравнения для картографической проекции и обратной Фуллера» . Cartographica: Международный журнал географической информации и геовизуализации . 43 (1): 67–72. дои : 10.3138/carto.43.1.67 . ISSN 0317-7173 .
- ^ Крайдер, Джон Э. (1 января 2009 г.). «Геодезическая картографическая проекция четырехугольников» . Картография и географическая информатика . 36 (2): 131–147. дои : 10.1559/152304009788188781 . ISSN 1523-0406 . S2CID 128390865 .
- ^ Сахр, Кевин; Уайт, Денис; Кимерлинг, Эй Джей (2003). «Геодезические дискретные глобальные сеточные системы» (PDF) . Картография и географическая информатика . 30 (2): 121–134. дои : 10.1559/152304003100011090 . S2CID 16549179 .
- ^ Адамс, Оскар С. (1925). Эллиптические функции в применении к конформным картам мира . Выпуск 297 сериала «Береговая и геодезическая служба США». Типография правительства США.
- ^ Л. П. Ли (1976). «Конформные проекции на основе эллиптических функций» . Картографика . 13 (Монография 16, приложение № 1 к «Канадскому картографу»).
- ^ Шил, Юджин (19 мая 2002 г.). «Обладая интеллектом и артистизмом, Веллман Чемберлин создал свой собственный мир» . Вашингтон Пост .
- ^ «Глобальная погоня (1987)» . Настольные игрыGeek . Проверено 30 августа 2022 г.
- ^ Чан, ФК; О'Нил, EM (1975). Технико-экономическое обоснование базы данных о Земле в форме четырехстороннего сферического куба (CSC - Computer Sciences Corporation, Технический отчет EPRF 2-75) (Технический отчет). Монтерей, Калифорния: Исследовательский центр по прогнозированию окружающей среды.
- ^ О'Нил, EM (1976). Расширенные исследования базы данных о Земле в форме четырехстороннего сферического куба (PDF) (Технический отчет). Монтерей, Калифорния: Исследовательский центр по прогнозированию окружающей среды. Архивировано (PDF) из оригинала 7 мая 2019 г.