Электрический дипольный момент

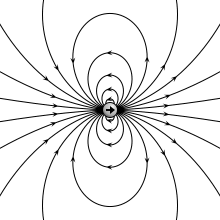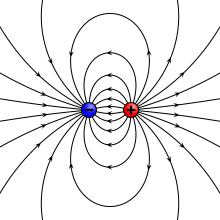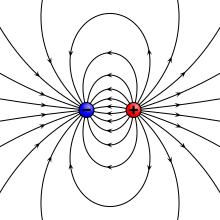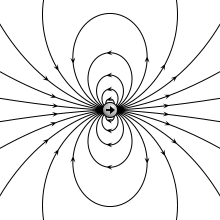
Электрическое поле, создаваемое точечным диполем (вверху слева), физическим диполем электрических зарядов (вверху справа), тонким поляризованным листом (внизу слева) или пластинчатым конденсатором (внизу справа). Все они генерируют одинаковый профиль поля, когда расположение бесконечно мало.
Общие символы	п
И объединились	Кулон - метр (См)
В базовых единицах СИ	m ⋅ s ⋅ A
Измерение	LTI

Электрический дипольный момент является мерой разделения положительных и отрицательных электрических зарядов системы внутри системы: то есть мерой общей полярности . Единицей момента в системе СИ электрического дипольного является кулон - метр (Кл⋅м). Дебай . (D) — еще одна единица измерения, используемая в атомной физике и химии

Теоретически электрический диполь определяется членом первого порядка мультипольного разложения ; он состоит из двух равных и противоположных зарядов, находящихся бесконечно близко друг к другу, хотя настоящие диполи имеют разделенный заряд.

Элементарное определение

Величины, определяющие электрический дипольный момент двух точечных зарядов.

Анимация, показывающая электрическое поле электрического диполя. Диполь состоит из двух точечных электрических зарядов противоположной полярности, расположенных близко друг к другу. Показана трансформация точечного диполя в электрический диполь конечного размера.

Молекула воды полярна из-за неравного распределения ее электронов в «изогнутой» структуре. Присутствует разделение заряда: отрицательный заряд посередине (красный оттенок) и положительный заряд на концах (синий оттенок).

Часто в физике размеры объекта можно игнорировать, поэтому его можно рассматривать как точечный объект, то есть точечную частицу . Точечные частицы, обладающие электрическим зарядом, называются точечными зарядами . Два точечных заряда, один с зарядом + q , а другой с зарядом − q, разделенные расстоянием d , составляют электрический диполь (простой случай электрического мультиполя ). В этом случае электрический дипольный момент имеет величину $$p=qd$$ и направлен от отрицательного заряда к положительному. Некоторые авторы могут разделить d пополам и использовать s = d /2, поскольку эта величина представляет собой расстояние между любым зарядом и центром диполя, что приводит к коэффициенту два в определении.

Более сильное математическое определение состоит в использовании векторной алгебры , поскольку величина с величиной и направлением, такая как дипольный момент двух точечных зарядов, может быть выражена в векторной форме. $$\mathbf {p} =q\mathbf {d}$$ где d — вектор смещения , направленный от отрицательного заряда к положительному заряду. Вектор электрического дипольного момента p также направлен от отрицательного заряда к положительному заряду. Согласно этому определению, направление диполя имеет тенденцию выравниваться с внешним электрическим полем (и обратите внимание, что линии электрического потока, создаваемые зарядами самого диполя, которые направлены от положительного заряда к отрицательному заряду, затем имеют тенденцию противодействовать линиям потока диполя). внешнее поле). Обратите внимание, что это соглашение о знаках используется в физике, в то время как противоположное соглашение о знаках для диполя, от положительного заряда к отрицательному заряду, используется в химии.

Идеализацией этой двухзарядной системы является электрический точечный диполь, состоящий из двух (бесконечных) зарядов, лишь бесконечно мало разделенных, но с конечным p . Эта величина используется при определении плотности поляризации .

Энергия и крутящий момент

Электрический диполь p и его крутящий момент τ в однородном электрическом поле.

На объект с электрическим дипольным моментом p действует крутящий момент τ, он помещен во внешнее электрическое поле E. когда Крутящий момент стремится выровнять диполь с полем. Диполь, ориентированный параллельно электрическому полю, имеет меньшую потенциальную энергию, чем диполь, составляющий с ним ненулевой угол. Для пространственно однородного электрического поля в малой области, занимаемой диполем, энергия U и момент ${\boldsymbol {\tau }}$ даны $$U=-\mathbf {p} \cdot \mathbf {E} ,\qquad \ {\boldsymbol {\tau }}=\mathbf {p} \times \mathbf {E} .$$

Скалярное точечное произведение « ⋅ » и отрицательный знак показывают, что потенциальная энергия минимальна, когда диполь параллелен полю, максимальна, когда он антипараллелен, и равна нулю, когда он перпендикулярен. Символ « × » относится к векторному векторному произведению . Вектор электронного поля и вектор диполя определяют плоскость, а крутящий момент направлен перпендикулярно этой плоскости с направлением, заданным правилом правой руки . Диполь в таком однородном поле может вращаться и колебаться, но не получает общей результирующей силы без линейного ускорения диполя. Диполь поворачивается, выравниваясь с внешним полем.

Однако в неоднородном электрическом поле диполь действительно может воспринимать результирующую силу, поскольку сила на одном конце диполя больше не уравновешивает силу на другом конце. Можно показать, что эта результирующая сила обычно параллельна дипольному моменту.

Выражение (общий случай)

В более общем смысле, для непрерывного распределения заряда, ограниченного объемом V , соответствующее выражение для дипольного момента имеет вид: $$\mathbf {p} (\mathbf {r} )=\int _{V}\rho (\mathbf {r} ')\left(\mathbf {r} '-\mathbf {r} \right)d^{3}\mathbf {r} ',$$

где r определяет точку наблюдения, а d ³ r ′ обозначает элементарный объём в V . Для массива точечных зарядов плотность заряда становится суммой дельта-функций Дирака : $$\rho (\mathbf {r} )=\sum _{i=1}^{N}\,q_{i}\,\delta \left(\mathbf {r} -\mathbf {r} _{i}\right),$$

где каждый r _i представляет собой вектор от некоторой точки отсчета до заряда q _i . Подстановка в приведенную выше формулу интегрирования дает: $$\mathbf {p} (\mathbf {r} )=\sum _{i=1}^{N}\,q_{i}\int _{V}\delta \left(\mathbf {r} _{0}-\mathbf {r} _{i}\right)\,\left(\mathbf {r} _{0}-\mathbf {r} \right)\,d^{3}\mathbf {r} _{0}=\sum _{i=1}^{N}\,q_{i}\left(\mathbf {r} _{i}-\mathbf {r} \right).$$

Это выражение эквивалентно предыдущему выражению в случае зарядовой нейтральности и N = 2. Для двух противоположных зарядов обозначение местоположения положительного заряда пары как r ₊ и расположение отрицательного заряда как r ₋ : $$\mathbf {p} (\mathbf {r} )=q_{1}(\mathbf {r} _{1}-\mathbf {r} )+q_{2}(\mathbf {r} _{2}-\mathbf {r} )=q(\mathbf {r} _{+}-\mathbf {r} )-q(\mathbf {r} _{-}-\mathbf {r} )=q(\mathbf {r} _{+}-\mathbf {r} _{-})=q\mathbf {d} ,$$

показывая, что вектор дипольного момента направлен от отрицательного заряда к положительному заряду, поскольку вектор положения точки направлен наружу от начала координат к этой точке.

Дипольный момент особенно полезен в контексте общей нейтральной системы зарядов, такой как пара противоположных зарядов или нейтральный проводник в однородном электрическом поле. Для такой системы, представленной как массив парных противоположных зарядов, соотношение для электрического дипольного момента имеет вид:

$${\begin{aligned}\mathbf {p} (\mathbf {r} )&=\sum _{i=1}^{N}\,\int _{V}q_{i}\left[\delta \left(\mathbf {r} _{0}-\left(\mathbf {r} _{i}+\mathbf {d} _{i}\right)\right)-\delta \left(\mathbf {r} _{0}-\mathbf {r} _{i}\right)\right]\,\left(\mathbf {r} _{0}-\mathbf {r} \right)\ d^{3}\mathbf {r} _{0}\\&=\sum _{i=1}^{N}\,q_{i}\,\left[\mathbf {r} _{i}+\mathbf {d} _{i}-\mathbf {r} -\left(\mathbf {r} _{i}-\mathbf {r} \right)\right]\\&=\sum _{i=1}^{N}q_{i}\mathbf {d} _{i}=\sum _{i=1}^{N}\mathbf {p} _{i}\,,\end{aligned}}$$

где r - точка наблюдения, а d _i = r ' _i - r _i , r _i - положение отрицательного заряда в диполе i , а r ' _i - положение положительного заряда.Это векторная сумма отдельных дипольных моментов пар нейтральных зарядов. (Из-за общей нейтральности заряда дипольный момент не зависит от положения наблюдателя r .) Таким образом, значение p не зависит от выбора точки отсчета, при условии, что общий заряд системы равен нулю.

При обсуждении дипольного момента ненейтральной системы, например дипольного момента протона , возникает зависимость от выбора точки отсчета. В таких случаях принято выбирать в качестве точки отсчета центр масс системы, а не какое-то произвольное начало координат. Этот выбор является не только вопросом соглашения: понятие дипольного момента по существу вытекает из механического понятия крутящего момента, и, как и в механике, с вычислительной и теоретической точки зрения полезно выбирать центр масс в качестве точки наблюдения. Для заряженной молекулы точкой отсчета должен быть центр заряда, а не центр масс. Для нейтральных систем точка отсчета не важна, а дипольный момент является внутренним свойством системы.

Потенциал и поле электрического диполя

Потенциальная карта физического электрического диполя. Отрицательные потенциалы выделены синим цветом; положительные потенциалы показаны красным.

Идеальный диполь состоит из двух противоположных зарядов, разделенных бесконечно малым расстоянием. Мы вычисляем потенциал и поле такого идеального диполя, начиная с двух противоположных зарядов на расстоянии d > 0 и переходя к пределу d → 0.

Два близко расположенных противоположных заряда ± q имеют потенциал вида: $$V(\mathbf {r} )\ =\ {\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{\left|\mathbf {r} -\mathbf {r} _{+}\right|}}-{\frac {q}{\left|\mathbf {r} -\mathbf {r} _{-}\right|}}\right),$$соответствующий плотности заряда $$\rho (\mathbf {r} )\ =\ -\varepsilon _{0}\nabla ^{2}V\ =\ q\delta \left(\mathbf {r} -\mathbf {r} _{+}\right)-q\delta \left(\mathbf {r} -\mathbf {r} _{-}\right)$$по закону Кулона ,где разделение зарядов: $$\mathbf {d} =\mathbf {r} _{+}-\mathbf {r} _{-}\,,\quad d=|\mathbf {d} |\,.$$

Обозначим через R вектор положения относительно средней точки. ${\frac {\mathbf {r} _{+}+\mathbf {r} _{-}}{2}}$, и ${\hat {\mathbf {R} }}$ соответствующий единичный вектор: $$\mathbf {R} =\mathbf {r} -{\frac {\mathbf {r} _{+}+\mathbf {r} _{-}}{2}},\quad {\hat {\mathbf {R} }}={\frac {\mathbf {R} }{|\mathbf {R} |}}\,,$$

Расширение Тейлора в ${\tfrac {d}{R}}$ (см. мультипольное разложение и квадруполь ) выражает этот потенциал в виде ряда. $$V(\mathbf {R} )\ =\ {\frac {1}{4\pi \varepsilon _{0}}}{\frac {q\mathbf {d} \cdot {\hat {\mathbf {R} }}}{R^{2}}}+{\mathcal {O}}\left({\frac {d^{3}}{R^{3}}}\right)\ \approx \ {\frac {1}{4\pi \varepsilon _{0}}}{\frac {\mathbf {p} \cdot {\hat {\mathbf {R} }}}{|\mathbf {R} |^{2}}}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {\mathbf {p} \cdot \mathbf {R} }{|\mathbf {R} |^{3}}}\,,$$где члены ряда более высокого порядка исчезают на больших расстояниях R по сравнению с d . Здесь электрический дипольный момент p равен, как указано выше: $$\mathbf {p} =q\mathbf {d} \,.$$

Результат для дипольного потенциала также можно выразить как: $$V(\mathbf {R} )\approx -\mathbf {p} \cdot \mathbf {\nabla } {\frac {1}{4\pi \varepsilon _{0}R}}\,,$$

которое связывает дипольный потенциал с потенциалом точечного заряда. Ключевым моментом является то, что потенциал диполя падает быстрее с расстоянием R, чем потенциал точечного заряда.

Электрическое поле диполя представляет собой отрицательный градиент потенциала, приводящий к: $$\mathbf {E} \left(\mathbf {R} \right)={\frac {3\left(\mathbf {p} \cdot {\hat {\mathbf {R} }}\right){\hat {\mathbf {R} }}-\mathbf {p} }{4\pi \varepsilon _{0}R^{3}}}\,.$$

Таким образом, хотя два близко расположенных противоположных заряда не являются вполне идеальным электрическим диполем (поскольку их потенциал на малых расстояниях не является потенциалом диполя), на расстояниях, значительно превышающих их расстояние, их дипольный момент р проявляется непосредственно в их потенциале и поле.

Когда два заряда сближаются ( d уменьшается), дипольный член в мультипольном разложении, основанном на отношении d / R, становится единственным значимым членом на все более близких расстояниях R , а в пределе бесконечно малого разделения дипольный член в этом расширении это все, что имеет значение. Однако, поскольку d делается бесконечно малым, заряд диполя должен увеличиваться, чтобы поддерживать p постоянным. Этот ограничивающий процесс приводит к образованию «точечного диполя».

Плотность дипольного момента и плотность поляризации

Дипольный момент массива зарядов, $$\mathbf {p} =\sum _{i=1}^{N}q_{i}\mathbf {d_{i}} \,,$$

определяет степень полярности массива, но для нейтрального массива это просто векторное свойство массива без информации об абсолютном местоположении массива. дипольного момента Плотность массива p ( r ) содержит как местоположение массива, так и его дипольный момент. Когда приходит время рассчитать электрическое поле в некоторой области, содержащей массив, уравнения Максвелла решаются, а информация о зарядовом массиве содержится в плотности поляризации P ( r ) уравнений Максвелла. В зависимости от того, насколько детальная оценка электрического поля требуется, более или менее информация о массиве зарядов должна быть выражена через P ( r ). Как поясняется ниже, иногда достаточно точно принять P ( r ) = p ( r ). Иногда необходимо более детальное описание (например, дополнение плотности дипольного момента дополнительной квадрупольной плотностью), а иногда еще более сложные варианты P ( r необходимы ).

Сейчас исследуется, каким образом плотность поляризации P ( r ), входящая в уравнения Максвелла, связана с дипольным моментом p всего нейтрального массива зарядов, а также с плотностью дипольного момента p ( r ) (которая описывает не только дипольный момент, но и расположение массива). Далее рассматриваются только статические ситуации, поэтому P ( r отсутствует ) не зависит от времени и ток смещения . Сначала немного обсудим плотность поляризации P ( r ). За этим обсуждением следуют несколько конкретных примеров.

Формулировка уравнений Максвелла , основанная на разделении зарядов и токов на «свободные» и «связанные» заряды и токи, приводит к введению D- и P - полей: $$\mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} \,,$$где P называется плотностью поляризации . В этой формулировке дивергенция этого уравнения дает: $$\nabla \cdot \mathbf {D} =\rho _{f}=\varepsilon _{0}\nabla \cdot \mathbf {E} +\nabla \cdot \mathbf {P} \,,$$и поскольку член дивергенции в E представляет собой общий заряд, а ρ _f — «свободный заряд», у нас остается соотношение: $$\nabla \cdot \mathbf {P} =-\rho _{b}\,,$$где ρ _b — связанный заряд, под которым понимают разность плотностей полного и свободного заряда.

Кроме того, в отсутствие магнитных эффектов уравнения Максвелла указывают, что $$\nabla \times \mathbf {E} ={\boldsymbol {0}}\,,$$

что подразумевает $$\nabla \times \left(\mathbf {D} -\mathbf {P} \right)={\boldsymbol {0}}\,,$$

Применяя разложение Гельмгольца : $$\mathbf {D} -\mathbf {P} =-\nabla \varphi \,,$$для некоторого скалярного потенциала φ и: $$\nabla \cdot (\mathbf {D} -\mathbf {P} )=\varepsilon _{0}\nabla \cdot \mathbf {E} =\rho _{f}+\rho _{b}=-\nabla ^{2}\varphi \,.$$

Предположим, что заряды разделены на свободные и связанные, а потенциал разделен на

$$\varphi =\varphi _{f}+\varphi _{b}\,.$$

Удовлетворение граничных условий для φ можно произвольно разделить между φ _f и φ _b , поскольку только сумма φ должна удовлетворять этим условиям. Отсюда следует, что P просто пропорционально электрическому полю, обусловленному зарядами, выбранными в качестве связанных, с граничными условиями, которые оказываются удобными. В частности, когда свободный заряд отсутствует , одним из возможных вариантов является P = ε ₀ E .

Далее обсуждается, как несколько различных описаний дипольного момента среды связаны с поляризацией, входящей в уравнения Максвелла.

Среда с зарядовой и дипольной плотностью

Как описано далее, модель плотности поляризационного момента p ( r ) приводит к поляризации $$\mathbf {P} (\mathbf {r} )=\mathbf {p} (\mathbf {r} )$$ограничено одной и той же моделью. Для плавно меняющегося распределения дипольного момента p ( r ) соответствующая плотность связанного заряда просто равна $$\nabla \cdot \mathbf {p} (\mathbf {r} )=-\rho _{b},$$как мы вскоре установим путем интеграции по частям . Однако, если p ( r ) демонстрирует резкий скачок дипольного момента на границе между двумя областями, ∇· p ( r ) приводит к образованию поверхностного зарядового компонента связанного заряда. Этот поверхностный заряд можно рассматривать с помощью поверхностного интеграла или с помощью условий разрыва на границе, как показано в различных примерах ниже.

В качестве первого примера связи дипольного момента с поляризацией рассмотрим среду, состоящую из непрерывной плотности заряда ρ ( r ) и непрерывного распределения дипольного момента p ( r ). Потенциал в позиции r равен: $$\phi (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho \left(\mathbf {r} _{0}\right)}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}d^{3}\mathbf {r} _{0}\ +{\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\mathbf {p} \left(\mathbf {r} _{0}\right)\cdot \left(\mathbf {r} -\mathbf {r} _{0}\right)}{|\mathbf {r} -\mathbf {r} _{0}|^{3}}}d^{3}\mathbf {r} _{0},$$

где ρ ( r ) — плотность неспаренного заряда, а p ( r ) — плотность дипольного момента. Использование удостоверения: $$\nabla _{\mathbf {r} _{0}}{\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}={\frac {\mathbf {r} -\mathbf {r} _{0}}{\left|\mathbf {r} -\mathbf {r} _{0}\right|^{3}}}$$поляризационный интеграл можно преобразовать: $${\begin{aligned}{\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\mathbf {p} \left(\mathbf {r} _{0}\right)\cdot (\mathbf {r} -\mathbf {r} _{0})}{\left|\mathbf {r} -\mathbf {r} _{0}\right|^{3}}}d^{3}\mathbf {r} _{0}={}&{\frac {1}{4\pi \varepsilon _{0}}}\int \mathbf {p} \left(\mathbf {r} _{0}\right)\cdot \nabla _{\mathbf {r} _{0}}{\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}d^{3}\mathbf {r} _{0},\\={}&{\frac {1}{4\pi \varepsilon _{0}}}\int \nabla _{\mathbf {r} _{0}}\cdot \left(\mathbf {p} \left(\mathbf {r} _{0}\right){\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\right)d^{3}\mathbf {r} _{0}-{\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\nabla _{\mathbf {r} _{0}}\cdot \mathbf {p} \left(\mathbf {r} _{0}\right)}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}d^{3}\mathbf {r} _{0},\end{aligned}}$$где векторное тождество $$\nabla \cdot (\mathbf {A} {B})=(\nabla \cdot \mathbf {A} ){B}+\mathbf {A} \cdot (\nabla {B})\implies \mathbf {A} \cdot (\nabla {B})=\nabla \cdot (\mathbf {A} {B})-(\nabla \cdot \mathbf {A} ){B}$$ использовался на последних шагах. Первый член можно преобразовать в интеграл по поверхности, ограничивающей объем интегрирования, и он вносит вклад в поверхностную плотность заряда, которая будет обсуждаться позже. Возвращая этот результат в потенциал и пока игнорируя поверхностный заряд: $$\phi (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho \left(\mathbf {r} _{0}\right)-\nabla _{\mathbf {r} _{0}}\cdot \mathbf {p} \left(\mathbf {r} _{0}\right)}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}d^{3}\mathbf {r} _{0}\,,$$где объемное интегрирование распространяется только до ограничивающей поверхности и не включает эту поверхность.

Потенциал определяется общим зарядом, который, как показано выше, состоит из: $$\rho _{\text{total}}\left(\mathbf {r} _{0}\right)=\rho \left(\mathbf {r} _{0}\right)-\nabla _{\mathbf {r} _{0}}\cdot \mathbf {p} \left(\mathbf {r} _{0}\right)\,,$$показывая, что: $$-\nabla _{\mathbf {r} _{0}}\cdot \mathbf {p} \left(\mathbf {r} _{0}\right)=\rho _{b}\,.$$

Короче говоря, плотность дипольного момента p ( r ) играет роль плотности поляризации P для этой среды. Обратите внимание, что p ( r ) имеет ненулевую дивергенцию, равную связанной плотности заряда (как моделируется в этом приближении).

Можно отметить, что этот подход можно расширить, включив в него все мультиполи: диполь, квадруполь и т. д. Используя отношение: $$\nabla \cdot \mathbf {D} =\rho _{f}\,,$$

плотность поляризации равна: $$\mathbf {P} (\mathbf {r} )=\mathbf {p} _{\text{dip}}-\nabla \cdot \mathbf {p} _{\text{quad}}+\cdots \,,$$

где добавленные члены предназначены для обозначения вкладов более высоких мультиполей. Очевидно, включение высших мультиполей означает, что плотность поляризации P больше не определяется только плотностью дипольного момента p . Например, при рассмотрении рассеяния на массиве зарядов разные мультиполи рассеивают электромагнитную волну по-разному и независимо, что требует представления зарядов, выходящего за рамки дипольного приближения.

Поверхностный заряд

Однородный массив одинаковых диполей эквивалентен поверхностному заряду.

Выше обсуждение было отложено до первого члена в выражении для потенциала, обусловленного диполями. Интегрирование расхождения приводит к поверхностному заряду. Рисунок справа дает интуитивное представление о том, почему возникает поверхностный заряд. На рисунке показан однородный массив одинаковых диполей между двумя поверхностями. Внутри головки и хвосты диполей соседствуют и взаимно нейтрализуются. Однако на ограничивающих поверхностях отмены не происходит. Вместо этого на одной поверхности головки диполя создают положительный поверхностный заряд, а на противоположной поверхности хвосты диполя создают отрицательный поверхностный заряд. Эти два противоположных поверхностных заряда создают суммарное электрическое поле в направлении, противоположном направлению диполей.

Этой идее придается математическая форма с использованием приведенного выше потенциального выражения. Если игнорировать бесплатную плату, потенциал: $$\phi \left(\mathbf {r} \right)={\frac {1}{4\pi \varepsilon _{0}}}\int \nabla _{\mathbf {r} _{0}}\cdot \left(\mathbf {p} \left(\mathbf {r} _{0}\right){\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\right)d^{3}\mathbf {r} _{0}-{\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\nabla _{\mathbf {r} _{0}}\cdot \mathbf {p} \left(\mathbf {r} _{0}\right)}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}d^{3}\mathbf {r} _{0}\,.$$

Используя теорему о дивергенции , член дивергенции преобразуется в поверхностный интеграл: $${\frac {1}{4\pi \varepsilon _{0}}}\int \nabla _{\mathbf {r} _{0}}\cdot \left(\mathbf {p} \left(\mathbf {r} _{0}\right){\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\right)d^{3}\mathbf {r} _{0}={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\mathbf {p} \left(\mathbf {r} _{0}\right)\cdot d\mathbf {A} _{0}}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\,,$$

где d A ₀ — элемент площади поверхности объема. В случае, если p ( r ) является константой, сохраняется только поверхностный член: $$\phi (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\ \mathbf {p} \cdot d\mathbf {A} _{0}\,,$$где d A ₀ — элементарный участок поверхности, ограничивающей заряды. Другими словами, потенциал, обусловленный постоянным p внутри поверхности, эквивалентен потенциалу поверхностного заряда. $$\sigma =\mathbf {p} \cdot d\mathbf {A}$$который положителен для элементов поверхности с компонентом в направлении p и отрицателен для элементов поверхности, направленных противоположно. (Обычно направление элемента поверхности принимается как направление внешней нормали к поверхности в месте расположения элемента.)

Если ограничивающая поверхность представляет собой сферу, а точка наблюдения находится в центре этой сферы, то интегрирование по поверхности сферы равно нулю: вклады положительного и отрицательного поверхностного заряда в потенциал компенсируются. Однако если точка наблюдения смещена от центра, может возникнуть чистый потенциал (в зависимости от ситуации), поскольку положительные и отрицательные заряды находятся на разных расстояниях от точки наблюдения. Поле, обусловленное поверхностным зарядом, равно: $$\mathbf {E} \left(\mathbf {r} \right)=-{\frac {1}{4\pi \varepsilon _{0}}}\nabla _{\mathbf {r} }\int {\frac {1}{\left|\mathbf {r} -\mathbf {r} _{0}\right|}}\ \mathbf {p} \cdot d\mathbf {A} _{0}\,,$$который в центре сферической ограничивающей поверхности не равен нулю ( поля отрицательных и положительных зарядов на противоположных сторонах центра складываются, поскольку оба поля направлены в одну и ту же сторону), а вместо этого равен: $$\mathbf {E} =-{\frac {\mathbf {p} }{3\varepsilon _{0}}}\,.$$

Если предположить, что поляризация диполей была вызвана внешним полем, то поле поляризации противодействует приложенному полю и иногда называется полем деполяризации . В случае, когда поляризация находится вне сферической полости, поле в полости, обусловленное окружающими диполями, направлено в том же направлении, что и поляризация.

В частности, если электрическую восприимчивость ввести через приближение: $$\mathbf {p} (\mathbf {r} )=\varepsilon _{0}\chi (\mathbf {r} )\mathbf {E} (\mathbf {r} )\,,$$где E в этом и последующих случаях представляет собой внешнее поле , вызывающее поляризацию.

Затем: $$\nabla \cdot \mathbf {p} (\mathbf {r} )=\nabla \cdot \left(\chi (\mathbf {r} )\varepsilon _{0}\mathbf {E} (\mathbf {r} )\right)=-\rho _{b}\,.$$

Всякий раз, когда χ ( r ) используется для моделирования ступенчатого разрыва на границе между двумя областями, ступенька создает слой поверхностного заряда. Например, интегрирование по нормали к ограничивающей поверхности от точки, находящейся непосредственно внутри одной поверхности, до другой точки, расположенной непосредственно снаружи: $$\varepsilon _{0}{\hat {\mathbf {n} }}\cdot \left[\chi \left(\mathbf {r} _{+}\right)\mathbf {E} \left(\mathbf {r} _{+}\right)-\chi \left(\mathbf {r} _{-}\right)\mathbf {E} \left(\mathbf {r} _{-}\right)\right]={\frac {1}{A_{n}}}\int d\Omega _{n}\ \rho _{b}=0\,,$$

где An _{обозначают} , Ω _n площадь и объем элементарной области, лежащей на границе между областями, и ${\hat {\mathbf {n} }}$ единица, нормальная к поверхности. Правая часть исчезает при уменьшении объема, поскольку ρ _b конечно, что указывает на разрыв E и, следовательно, на поверхностный заряд. То есть там, где моделируемая среда включает ступеньку диэлектрической проницаемости, плотность поляризации, соответствующая плотности дипольного момента $$\mathbf {p} (\mathbf {r} )=\chi (\mathbf {r} )\mathbf {E} (\mathbf {r} )$$

обязательно включает вклад поверхностного заряда.

Физически более реалистичное моделирование p ( r ) привело бы к быстрому, но плавному падению плотности дипольного момента до нуля на границе удерживающей области, а не к внезапному скачку к нулевой плотности. Тогда поверхностный заряд не будет концентрироваться в бесконечно тонкой поверхности, а, являясь дивергенцией плавно меняющейся плотности дипольного момента, распределится по тонкому, но конечному переходному слою.

Диэлектрическая сфера в однородном внешнем электрическом поле

Силовые линии в D -поля диэлектрической сфере с большей восприимчивостью, чем ее окружение, помещенной в ранее однородное поле. Е Силовые линии ( - поля не показаны) всюду совпадают с линиями D -поля, но внутри сферы их плотность ниже, что соответствует тому, что Е -поле внутри сферы слабее, чем снаружи. Многие из внешних силовых линий Е -поля оканчиваются на поверхности сферы, где находится связанный заряд.

Приведенные выше общие замечания о поверхностном заряде становятся более конкретными на примере диэлектрической сферы в однородном электрическом поле. Обнаружено, что сфера принимает поверхностный заряд, связанный с дипольным моментом внутри нее.

Предполагается, что однородное внешнее электрическое поле направлено в направлении z , и вводятся сферически-полярные координаты, поэтому потенциал, создаваемый этим полем, равен: $$\phi _{\infty }=-E_{\infty }z=-E_{\infty }r\cos \theta \,.$$

Предполагается, что сфера описывается диэлектрической постоянной κ , т.е. $$\mathbf {D} =\kappa \varepsilon _{0}\mathbf {E} \,,$$

а внутри сферы потенциал удовлетворяет уравнению Лапласа. Опуская несколько деталей, решение внутри сферы таково: $$\phi _{<}=Ar\cos \theta \,,$$

находясь вне сферы: $$\phi _{>}=\left(Br+{\frac {C}{r^{2}}}\right)\cos \theta \,.$$

На больших расстояниях φ _> → φ _∞, поэтому B = − E _∞ . Непрерывность потенциала и радиальной составляющей смещения D = κε ₀ E определяют две другие константы. Предположим, что радиус сферы равен R , $$A=-{\frac {3}{\kappa +2}}E_{\infty }\ ;\ C={\frac {\kappa -1}{\kappa +2}}E_{\infty }R^{3}\,,$$

Как следствие, потенциал: $$\phi _{>}=\left(-r+{\frac {\kappa -1}{\kappa +2}}{\frac {R^{3}}{r^{2}}}\right)E_{\infty }\cos \theta \,,$$который представляет собой потенциал, обусловленный приложенным полем и, кроме того, диполем в направлении приложенного поля ( направление z ) дипольного момента: $$\mathbf {p} =4\pi \varepsilon _{0}\left({\frac {\kappa -1}{\kappa +2}}R^{3}\right)\mathbf {E} _{\infty }\,,$$

или на единицу объема: $${\frac {\mathbf {p} }{V}}=3\varepsilon _{0}\left({\frac {\kappa -1}{\kappa +2}}\right)\mathbf {E} _{\infty }\,.$$

Множитель ( κ − 1)/( κ + 2) называется фактором Клаузиуса–Моссотти и показывает, что индуцированная поляризация меняет знак, если κ < 1. Конечно, в этом примере этого произойти не может, но в примере с двумя разными диэлектриков κ заменяется отношением диэлектрических проницаемостей внутренней и внешней областей, которое может быть больше или меньше единицы. Потенциал внутри сферы: $$\phi _{<}=-{\frac {3}{\kappa +2}}E_{\infty }r\cos \theta \,,$$

ведущие к полю внутри сферы: $$-\nabla \phi _{<}={\frac {3}{\kappa +2}}\mathbf {E} _{\infty }=\left(1-{\frac {\kappa -1}{\kappa +2}}\right)\mathbf {E} _{\infty }\,,$$

демонстрирующий деполяризующий эффект диполя. Обратите внимание, что поле внутри сферы однородно и параллельно приложенному полю. Дипольный момент однороден внутри сферы. Поверхностная плотность заряда на сфере представляет собой разность радиальных компонент поля: $$\sigma =3\varepsilon _{0}{\frac {\kappa -1}{\kappa +2}}E_{\infty }\cos \theta ={\frac {1}{V}}\mathbf {p} \cdot {\hat {\mathbf {R} }}\,.$$

Этот пример линейного диэлектрика показывает, что подход к диэлектрической проницаемости эквивалентен модели однородного дипольного момента и приводит к нулевому заряду везде, за исключением поверхностного заряда на границе сферы.

Общие СМИ

Если наблюдение ограничивается областями, достаточно удаленными от системы зарядов, можно осуществить мультипольное разложение точной плотности поляризации. Усекая это разложение (например, сохраняя только дипольные члены или только дипольные и квадрупольные члены и т. д. ), результаты предыдущего раздела восстанавливаются. В частности, если сократить разложение на дипольном члене, результат будет неотличим от плотности поляризации, создаваемой однородным дипольным моментом, ограниченным областью заряда. С точностью до этого дипольного приближения, как показано в предыдущем разделе, плотность дипольного момента p ( r ) (которая включает не только p , но и местоположение p ) служит P ( r ).

В местах внутри массива зарядов для подключения массива парных зарядов к приближению, включающему только плотность дипольного момента p ( r ), требуются дополнительные соображения. Простейшее приближение — заменить массив зарядов моделью идеальных (бесконечно малых) диполей. В частности, как и в приведенном выше примере, в котором используется постоянная плотность дипольного момента, ограниченная конечной областью, в результате возникает поверхностный заряд и поле деполяризации. Более общая версия этой модели (которая позволяет поляризации меняться в зависимости от положения) — это обычный подход, использующий электрическую восприимчивость или электрическую проницаемость .

Более сложная модель массива точечных зарядов вводит эффективную среду путем усреднения микроскопических зарядов; например, при усреднении можно сделать так, что роль будут играть только дипольные поля. Связанный подход состоит в том, чтобы разделить заряды на заряды, находящиеся рядом с точкой наблюдения, и заряды, находящиеся достаточно далеко, чтобы обеспечить мультипольное расширение. Близлежащие заряды тогда вызывают локальные эффекты поля . В распространенной модели этого типа удаленные заряды рассматриваются как однородная среда с использованием диэлектрической проницаемости, а близлежащие заряды рассматриваются только в дипольном приближении. Аппроксимацию среды или массива зарядов только диполями и связанной с ними плотностью дипольного момента иногда называют приближением точечного диполя , приближением дискретного диполя или просто приближением диполя .

Электрические дипольные моменты фундаментальных частиц

Не путать со спином , который относится к магнитным дипольным моментам частиц, продолжается большая экспериментальная работа по измерению электрических дипольных моментов (ЭДМ; или аномального электрического дипольного момента ) фундаментальных и составных частиц, а именно электрона и нейтрона . соответственно. Поскольку EDM нарушают как симметрию четности (P), так и симметрию обращения времени (T), их значения дают в основном независимую от модели меру CP-нарушения в природе (при условии, что симметрия CPT действительна). Следовательно, значения этих EDM накладывают строгие ограничения на масштаб CP-нарушений, которые могут допускать расширения стандартной модели физики элементарных частиц . Текущие поколения экспериментов разработаны с учетом диапазона суперсимметрии EDM, обеспечивая дополнительные эксперименты к экспериментам, проводимым на БАК .

Действительно, многие теории несовместимы с текущими ограничениями и фактически исключены, а устоявшаяся теория допускает гораздо большее значение, чем эти пределы, что приводит к сильной проблеме CP и побуждает к поиску новых частиц, таких как аксион .

По крайней мере в секторе Юкава мы знаем по колебаниям нейтральных каонов, что CP нарушен. Были проведены эксперименты по измерению электрического дипольного момента различных частиц, таких как электрон и нейтрон . Многие модели, выходящие за рамки стандартной модели , с дополнительными членами, нарушающими CP, в общем предсказывают ненулевой электрический дипольный момент и, следовательно, чувствительны к такой новой физике. Инстантонные поправки от ненулевого члена θ в квантовой хромодинамике предсказывают ненулевой электрический дипольный момент для нейтрона и протона, который не наблюдался в экспериментах (где лучшие оценки получены при анализе нейтронов). Это сильная CP-проблема , предсказанная киральной теорией возмущений .

Дипольные моменты молекул

Дипольные моменты в молекулах ответственны за поведение вещества во внешних электрических полях. Диполи имеют тенденцию ориентироваться на внешнее поле, которое может быть постоянным или зависеть от времени. Этот эффект лежит в основе современной экспериментальной техники, называемой диэлектрической спектроскопией .

Дипольные моменты можно обнаружить в обычных молекулах, таких как вода, а также в биомолекулах, таких как белки.

С помощью полного дипольного момента некоторого материала можно вычислить диэлектрическую проницаемость, которая связана с более интуитивной концепцией проводимости. Если ${\mathcal {M}}_{\rm {Tot}}$ - полный дипольный момент образца, тогда диэлектрическая проницаемость определяется выражением: $$\varepsilon =1+k\left\langle {\mathcal {M}}_{\text{Tot}}^{2}\right\rangle$$где k — константа и $\left\langle {\mathcal {M}}_{\text{Tot}}^{2}\right\rangle =\left\langle {\mathcal {M}}_{\text{Tot}}(t=0){\mathcal {M}}_{\text{Tot}}(t=0)\right\rangle$ – временная корреляционная функция полного дипольного момента. В общем, общий дипольный момент имеет вкладот перемещений и вращений молекул в образце, $${\mathcal {M}}_{\text{Tot}}={\mathcal {M}}_{\text{Trans}}+{\mathcal {M}}_{\text{Rot}}.$$

Следовательно, диэлектрическая проницаемость (и проводимость) имеют вклад от обоих членов. Этот подход можно обобщить для расчета частотно-зависимой диэлектрической функции.

Дипольные моменты можно рассчитать из теории электронной структуры либо как реакцию на постоянные электрические поля, либо из матрицы плотности. Однако такие значения невозможно напрямую сравнить с экспериментом из-за потенциального присутствия ядерных квантовых эффектов, которые могут быть существенными даже для простых систем, таких как молекула аммиака. Теория связанных кластеров (особенно CCSD(T) ) может давать очень точные дипольные моменты, хотя можно получить разумные оценки (в пределах примерно 5%) из теории функционала плотности , особенно если гибридные или двойные гибридные функционалы. используются Дипольный момент молекулы также можно рассчитать на основе молекулярной структуры, используя концепцию методов группового вклада.

См. также

• Аномальный магнитный дипольный момент
• Дипольный момент связи
• Электрический дипольный момент нейтрона
• Электрический дипольный момент электрона
• Тороидальный дипольный момент
• Динамический тороидальный диполь
• Многополюсное расширение
• Многополюсные моменты
• Сплошные гармоники
• Осевые мультипольные моменты
• Цилиндрические мультипольные моменты
• Сферические мультипольные моменты
• Расширение Лапласа
• Полиномы Лежандра

Дальнейшее чтение

• Мелвин Шварц (1987). «Электрический ДИПОЛЬНЫЙ МОМЕНТ» . Принципы электродинамики (переиздание изд. 1972 г.). Публикации Курьера Дувра. п. 49 и далее . ISBN  978-0-486-65493-5 .

Внешние ссылки

• Электрический дипольный момент - из мира физики Эрика Вайсштейна
• Мультифизическая модель электростатического диполя