Пифагорова тройка

Анимация, демонстрирующая наименьшую тройку Пифагора, 3. ² + 4 ² = 5 ² .

Тройка Пифагора состоит из трёх натуральных чисел a , b и c , таких, что a ² + б ² = с ² . Такую тройку обычно пишут ( a , b , c ) , известный пример — (3, 4, 5) . Если ( a , b , c ) является тройкой Пифагора, то таковой является и ( ka , kb , kc ) для любого положительного целого числа k . Треугольник, длины сторон которого представляют собой тройку Пифагора, является прямоугольным треугольником и называется треугольником Пифагора .

Примитивная пифагорова тройка — это тройка, в которой a , b и c ( взаимно просты то есть не имеют общего делителя, большего 1). Например, (3, 4, 5) является примитивной пифагоровой тройкой, а (6, 8, 10) — нет. Каждую пифагорову тройку можно масштабировать до уникальной примитивной пифагоровой тройки путем деления ( a , b , c ) на их наибольший общий делитель . И наоборот, каждую тройку Пифагора можно получить умножением элементов примитивной тройки Пифагора на положительное целое число (то же самое для трех элементов).

Название происходит от теоремы Пифагора , утверждающей, что у каждого прямоугольного треугольника длины сторон удовлетворяют формуле $a^{2}+b^{2}=c^{2}$; таким образом, тройки Пифагора описывают три целые длины сторон прямоугольного треугольника. Однако прямоугольные треугольники с нецелыми сторонами не образуют пифагоровы тройки. Например, треугольник со сторонами $a=b=1$ и $c={\sqrt {2}}$ треугольник прямоугольный, но $(1,1,{\sqrt {2}})$ не является тройкой Пифагора, поскольку квадратный корень из 2 не является целым числом или отношением целых чисел . Более того, $1$ и ${\sqrt {2}}$ не имеют целого общего кратного, потому что ${\sqrt {2}}$ является иррациональным .

Пифагоровы тройки известны с древних времен. Самая старая известная запись происходит от Плимптона 322 , вавилонской глиняной таблички примерно 1800 года до нашей эры, написанной в шестидесятеричной системе счисления.

При поиске целочисленных решений уравнение a ² + б ² = с ² является диофантовым уравнением . Таким образом, тройки Пифагора являются одними из старейших известных решений нелинейного диофантова уравнения.

Примеры

Диаграмма рассеяния ветвей ( a , b ) первых троек Пифагора с a и b меньше 6000. Отрицательные значения включены для иллюстрации параболических моделей. «Лучи» являются результатом того факта, что если ( a , b , c ) является пифагоровой тройкой, то также и (2 a , 2 b , 2 c ) , (3 a , 3 b , 3 c ) и, в более общем смысле, ( ka , kb , kc ) для любого положительного целого числа k .

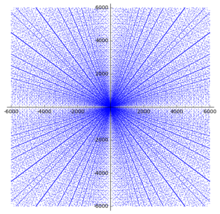
Существует 16 примитивных пифагорейских троек чисел до 100:

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7, 24, 25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)

Другие маленькие пифагоровы тройки, такие как (6, 8, 10), не указаны, поскольку они не примитивны; например (6, 8, 10) кратно (3, 4, 5).

Каждая из этих точек (с кратными им точками) образует расходящуюся линию на диаграмме рассеяния справа.

Кроме того, это оставшиеся примитивные пифагоровы тройки чисел до 300:

(20, 99, 101)	(60, 91, 109)	(15, 112, 113)	(44, 117, 125)
(88, 105, 137)	(17, 144, 145)	(24, 143, 145)	(51, 140, 149)
(85, 132, 157)	(119, 120, 169)	(52, 165, 173)	(19, 180, 181)
(57, 176, 185)	(104, 153, 185)	(95, 168, 193)	(28, 195, 197)
(84, 187, 205)	(133, 156, 205)	(21, 220, 221)	(140, 171, 221)
(60, 221, 229)	(105, 208, 233)	(120, 209, 241)	(32, 255, 257)
(23, 264, 265)	(96, 247, 265)	(69, 260, 269)	(115, 252, 277)
(160, 231, 281)	(161, 240, 289)	(68, 285, 293)

Создание тройки

Основная статья: Формулы для создания троек Пифагора

Примитивные пифагорейские тройки. Нечетный участок a откладывается по горизонтальной оси, четный участок b — по вертикальной. Криволинейная сетка состоит из кривых постоянной m - n и постоянной m + n в формуле Евклида.

График троек, созданный по формуле Евклида, отображает часть z ² = х ² + и ² конус. Постоянная m или n очерчивает часть параболы на конусе.

Формула Евклида — это фундаментальная формула для создания троек Пифагора по произвольной паре целых чисел m и n с m > n > 0 . Формула гласит, что целые числа

$a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}$

образуют пифагорову тройку. Например, учитывая

$m=2,\ \,n=1$

сгенерируйте примитивную тройку (3,4,5):

$a=2^{2}-1^{2}=3,\ \,b=2\times 2\times 1=4,\ \,c=2^{2}+1^{2}=5.$

Тройка, порожденная формулой Евклида , является примитивной тогда и только тогда, когда m и n взаимно просты и ровно один из них четен. Если и m , и n нечетны, то a , b и c будут четными, а тройка не будет примитивной; однако деление a , b и c на 2 даст примитивную тройку, когда m и n взаимно просты.

Каждая примитивная тройка возникает (после замены a и b , если a четное) из единственной пары взаимно простых чисел m , n , одно из которых четное. Отсюда следует, что существует бесконечно много примитивных пифагоровых троек. Эта связь a , b и c с m и n из формулы Евклида упоминается в оставшейся части этой статьи.

Несмотря на создание всех примитивных троек, формула Евклида не создает все тройки — например, (9, 12, 15) не может быть сгенерировано с использованием целых чисел m и n . Это можно исправить, вставив дополнительный параметр k в формулу . Следующие команды однозначно генерируют все пифагоровы тройки:

$a=k\cdot (m^{2}-n^{2}),\ \,b=k\cdot (2mn),\ \,c=k\cdot (m^{2}+n^{2})$

где m , n и k — положительные целые числа с m > n и с m и n взаимно простыми, а не оба нечетными.

То, что эти формулы порождают тройки Пифагора, можно проверить, разложив ² + б ² используя элементарную алгебру и проверяя, что результат равен c ² . Поскольку каждую тройку Пифагора можно разделить на некоторое целое число k , чтобы получить примитивную тройку, каждую тройку можно сгенерировать уникальным образом, используя формулу с m и n для создания ее примитивного аналога, а затем умножая ее на k , как в последнем уравнении.

Выбор m и n из определенных целочисленных последовательностей дает интересные результаты. Например, если m и n — последовательные числа Пелля , a и b будут отличаться на 1.

Многие формулы для создания троек с определенными свойствами были разработаны со времен Евклида.

Доказательство формулы Евклида

удовлетворяет формуле Евклида То, что a, b, c для , достаточно того, чтобы треугольник был пифагорейским, очевидно из того факта, что для натуральных чисел m и n , m > n , a , b и c, заданные формулой, все положительны. целые числа, и из того, что

$a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}.$

Доказательство необходимости выражения а, b, с формулой Евклида для любой примитивной пифагоровой тройки состоит в следующем. Все такие примитивные тройки можно записать как ( a , b , c ) , где a ² + б ² = с ² и a , b , c взаимно просты . Таким образом , a , b , c попарно взаимно просты (если бы простое число делило два из них, оно было бы вынуждено разделить и третье). Поскольку a и b взаимно простые, по крайней мере один из них нечетный. Если мы предположим, что a нечетно, то b четно, а c нечетно (если бы b было нечетным, c было бы четным, а c ² будет кратно 4, а ² + б ² будет равен 2 по модулю 4, как нечетный квадрат равен 1 по модулю 4).

От $a^{2}+b^{2}=c^{2}$ предположим, что a нечетно. Мы получаем $c^{2}-a^{2}=b^{2}$ и, следовательно, $(c-a)(c+a)=b^{2}$. Затем ${\tfrac {(c+a)}{b}}={\tfrac {b}{(c-a)}}$. С ${\tfrac {(c+a)}{b}}$ рационально, мы полагаем его равным ${\tfrac {m}{n}}$ в самых низких условиях. Таким образом ${\tfrac {(c-a)}{b}}={\tfrac {n}{m}}$, являясь обратной величиной ${\tfrac {(c+a)}{b}}$. Затем решение

${\frac {c}{b}}+{\frac {a}{b}}={\frac {m}{n}},\quad \quad {\frac {c}{b}}-{\frac {a}{b}}={\frac {n}{m}}$

для ${\tfrac {c}{b}}$ и ${\tfrac {a}{b}}$ дает

${\frac {c}{b}}={\frac {1}{2}}\left({\frac {m}{n}}+{\frac {n}{m}}\right)={\frac {m^{2}+n^{2}}{2mn}},\quad \quad {\frac {a}{b}}={\frac {1}{2}}\left({\frac {m}{n}}-{\frac {n}{m}}\right)={\frac {m^{2}-n^{2}}{2mn}}.$

Как ${\tfrac {m}{n}}$ полностью редуцировано, m и n взаимно просты и не могут быть оба четными. Если бы они оба были нечетными, числитель ${\tfrac {m^{2}-n^{2}}{2mn}}$ будет кратно 4 (поскольку нечетный квадрат равен 1 по модулю 4), а знаменатель 2 mn не будет кратен 4. Поскольку 4 будет минимально возможным четным множителем в числителе, а 2 будет максимальным возможный четный фактор в знаменателе, это будет означать, что a будет четным, несмотря на то, что оно определено как нечетное. Таким образом, одна из m и n нечетная, а другая четная, а числители двух дробей со знаменателем 2 mn нечетные. Таким образом, эти дроби полностью сокращаются (нечетное простое число, делящее этот знаменатель, делит одно из m и n, но не другое; таким образом, оно не делит m ² ± н ² ). Таким образом, можно приравнять числители к числителям и знаменатели к знаменателям, давая формулу Евклида

$a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}$ с m и n взаимно простыми и противоположными четностями.

Более длинное, но более банальное доказательство дано у Маора (2007). и Серпинский (2003). Другое доказательство приведено в Диофантовом уравнении § Пример пифагоровых троек как пример общего метода, применимого к каждому однородному диофантову уравнению второй степени.

Интерпретация параметров в формуле Евклида

Предположим, что стороны треугольника Пифагора имеют длину m. ² − п ² , 2 мин и м ² + н ² , и предположим, что угол между катетами длиной m ² − п ² и гипотенуза длины m ² + н ² обозначается как β . Затем $\tan {\tfrac {\beta }{2}}={\tfrac {n}{m}}$ а полноугольные тригонометрические значения равны $\sin {\beta }={\tfrac {2mn}{m^{2}+n^{2}}}$, $\cos {\beta }={\tfrac {m^{2}-n^{2}}{m^{2}+n^{2}}}$, и $\tan {\beta }={\tfrac {2mn}{m^{2}-n^{2}}}$.

Вариант

Следующий вариант формулы Евклида иногда оказывается более удобным, поскольку он более симметричен по m и n (то же условие четности по m и n ).

Если m и n — два нечетных целых числа такие, что m > n , то

$a=mn,\quad b={\frac {m^{2}-n^{2}}{2}},\quad c={\frac {m^{2}+n^{2}}{2}}$

— три целых числа, образующих пифагорову тройку, которая примитивна тогда и только тогда, когда m и n взаимно просты. И наоборот, каждая примитивная пифагорова тройка возникает (после замены a и b , если a четное) из уникальной пары m > n > 0 взаимно простых нечетных целых чисел.

Не меняя местами a и b

В изложении выше сказано, что все пифагоровы тройки однозначно получаются из формулы Евклида «после замены a и b , если a четное». Чтобы избежать этого обмена, формулу Евклида и приведенный выше вариант можно объединить следующим образом, что приведет к следующему результату.

Любую примитивную пифагорову тройку можно записать однозначно.

$a=2\varepsilon mn,\quad b=\varepsilon (m^{2}-n^{2}),\quad c=\varepsilon (m^{2}+n^{2}),$

где m и n — положительные взаимно простые целые числа, а $\varepsilon ={\frac {1}{2}}$ если m и n оба нечетны, и $\varepsilon =1$ в противном случае. Эквивалентно, $\varepsilon ={\frac {1}{2}}$ если a нечетно, и $\varepsilon =1$ если а четное.

Элементарные свойства примитивных пифагоровых троек

Общие свойства

Свойства примитивной тройки Пифагора ( a , b , c ) с a < b < c (без указания того, какое из a или b четное, а какое нечетное) включают:

• ${\tfrac {(c-a)(c-b)}{2}}$ всегда идеальный квадрат. Поскольку это лишь необходимое, но не достаточное условие, его можно использовать для проверки того, не является ли данная тройка чисел пифагоровой тройкой. Например, каждая тройка {6, 12, 18} и {1, 8, 9} проходит тест на то, что ( c − a )( c − b )/2 является полным квадратом, но ни одна из них не является тройкой Пифагора.
• Когда тройка чисел a , b и c образует примитивную пифагорову тройку, тогда ( c минус четная часть) и половина ( c минус нечетная часть) являются идеальными квадратами; однако это не достаточное условие, поскольку числа {1, 8, 9} проходят тест идеальных квадратов, но не являются пифагоровой тройкой, поскольку 1 ² + 8 ² ≠ 9 ² .
• Не более одного из a , b , c является квадратом.
• Площадь треугольника Пифагора не может быть равна квадрату или в два раза больше квадрата целого числа.
• Ровно одно из a , b делится на 2 ( четно ), а гипотенуза c всегда нечетна.
• Ровно одно из a , b делится на 3, но никогда c .
• Ровно одно из a , b делится на 4, но никогда c (потому что c никогда не бывает четным).
• Ровно одно из a , b , c делится на 5.
• Наибольшее число, которое всегда делит abc, равно 60.
• Любое нечетное число вида 2 m +1 , где m — целое число и m >1 , может быть нечетной частью примитивной пифагоровой тройки. См . раздел о почти равнобедренных примитивных пифагорейских тройках ниже. Однако четной частью примитивной пифагоровой тройки могут быть только четные числа, делящиеся на 4. Это связано с тем, что формула Евклида для четного катета, приведенная выше, равна 2 mn , и один из m или n должен быть четным.
• Гипотенуза c (всегда нечетная) представляет собой сумму двух квадратов. Для этого требуется, чтобы все его простые множители были простыми числами вида 4 n + 1 . Следовательно, c имеет вид 4 n + 1 . Последовательность возможных чисел гипотенузы для примитивной пифагоровой тройки можно найти по адресу (последовательность A008846 в OEIS ).
• Площадь ( K = ab /2) — конгруэнтное число. делится на 6.
• В каждом треугольнике Пифагора радиус вписанной окружности и радиусы трех вписанных окружностей являются целыми положительными числами. В частности, для примитивной тройки радиус вписанной окружности равен r = n ( m − n ) , а радиусы вписанной окружности, противоположные сторонам m ² − п ² , 2mn и гипотенуза m ² + н ² соответственно m ( м - п ) , п ( м + п ) и м ( м + п ) .
• Что касается любого прямоугольного треугольника, обратная теорема Фалеса гласит, что диаметр описанной окружности равен гипотенузе; следовательно, для примитивных троек диаметр описанной окружности равен м. ² + н ² , а радиус описанной окружности равен половине этого значения и, следовательно, является рациональным, но нецелым (поскольку m и n имеют противоположную четность).
• Когда площадь треугольника Пифагора умножается на кривизну вписанной и трех вписанных в него окружностей, в результате получаются четыре положительных целых числа w > x > y > z соответственно. Целые числа — w , x , y , z удовлетворяют круговому уравнению Декарта . Эквивалентно, радиус внешнего круга Содди любого прямоугольного треугольника равен его полупериметру. Внешний центр Содди расположен в точке D , где ACBD — прямоугольник, ACB — прямоугольный треугольник, а AB — его гипотенуза.
• Только две стороны примитивной тройки Пифагора могут быть одновременно простыми, поскольку по формуле Евклида для образования примитивной тройки Пифагора одно из катетов должно быть составным и четным. Однако только одна сторона может быть целым числом совершенной степени. $p\geq 2$ потому что, если бы две стороны были целыми числами совершенной степени с одинаковым показателем $p$ это противоречило бы тому факту, что не существует целочисленных решений диофантова уравнения $x^{2p}\pm y^{2p}=z^{2}$, с $x$, $y$ и $z$ быть попарно взаимно простым.
• Не существует треугольников Пифагора, у которых гипотенуза и один катет являются катетами другого треугольника Пифагора; это одна из эквивалентных форм теоремы Ферма о прямоугольном треугольнике .
• имеет уникальное отношение площади K к квадрату полупериметра s Каждый примитивный треугольник Пифагора и определяется выражением

${\frac {K}{s^{2}}}={\frac {n(m-n)}{m(m+n)}}=1-{\frac {c}{s}}.$

• Ни один примитивный треугольник Пифагора не имеет целой высоты от гипотенузы; то есть каждый примитивный треугольник Пифагора неразложим.
• Набор всех примитивных пифагоровых троек образует корневое троичное дерево естественным образом ; см. Дерево примитивных пифагорейских троек .
• из острых углов треугольника Пифагора не может иметь рациональное число градусов Ни один . (Это следует из теоремы Нивена .)

Особые случаи

Кроме того, может гарантированно существовать специальные пифагоровы тройки с некоторыми дополнительными свойствами:

• Каждое целое число больше 2, которое не соответствует 2 по модулю 4 (другими словами, каждое целое число больше 2, которое не имеет формы 4 k + 2 ), является частью примитивной пифагоровой тройки. (Если целое число имеет вид 4 k можно взять n = 1 и m = 2 k , в формуле Евклида ; если целое число равно 2 k + 1 , можно взять n = k и m = k + 1. )
• Каждое целое число больше 2 является частью примитивной или непримитивной пифагоровой тройки. Например, целые числа 6, 10, 14 и 18 не являются частью примитивных троек, а являются частью непримитивных троек (6, 8, 10) , (14, 48, 50) и (18, 80, 82) .
• Существует бесконечно много пифагорейских троек, у которых гипотенуза и самый длинный катет отличаются ровно на единицу. Такие тройки обязательно примитивны и имеют вид (2 n + 1, 2 n ² + 2н , 2н ² + 2 н +1) . Это следует из формулы Евклида, когда он замечает, что из условия следует, что тройка примитивна и должна проверяться ( m ² + н ² ) - 2 мин = 1 . Это подразумевает ( m – n ) ² = 1 и, таким образом, m = n + 1 . Таким образом, приведенная выше форма троек является результатом замены m на n + 1 в формуле Евклида.
• Существует бесконечно много примитивных пифагорейских троек, в которых гипотенуза и самый длинный катет отличаются ровно на два. Все они примитивны и получаются помещением n = 1 в формулу Евклида. В более общем смысле, для каждого целого числа k > 0 существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и нечетный катет отличаются на 2 k. ² . Они получаются помещением n = k в формулу Евклида.
• Существует бесконечно много пифагорейских троек, в которых две ноги отличаются ровно на единицу. Например, 20 ² + 21 ² = 29 ² ; они генерируются по формуле Евклида, когда ${\tfrac {m-n}{n}}$ является конвергентной к ${\sqrt {2}}$.
• Для каждого натурального числа k существует k троек Пифагора с разными гипотенузами и одинаковой площадью.
• Для каждого натурального числа k существует не менее k различных примитивных троек Пифагора с одной и той же ножкой a , где a — некоторое натуральное число (длина четной ножки равна 2 mn , и достаточно выбрать a со многими факторизациями, например a = 4 b , где b — произведение k различных нечетных простых чисел, получается не менее 2; ^к различные примитивные тройки).
• Для каждого натурального числа k существует не менее k различных троек Пифагора с одинаковой гипотенузой.
• Если с = р ^и — степень простого числа , существует примитивная пифагорова тройка a ² + б ² = с ² тогда и только тогда, когда простое число p имеет вид 4 n + 1 ; эта тройка единственна с точностью до замены a и b .
• В более общем смысле, положительное целое число c является гипотенузой примитивной пифагоровой тройки тогда и только тогда, когда простой c делитель конгруэнтен по 1 4 модулю каждый ; то есть каждый простой множитель имеет вид 4 n + 1 . В этом случае количество примитивных пифагоровых троек ( a , b , c ) с a < b равно 2. ^{к -1} , где k — количество различных простых делителей числа c .
• Существует бесконечно много пифагорейских троек с квадратными числами как для гипотенузы c, так и для суммы катетов a + b . По Ферма, наименьшая такая тройка имеет стороны a = 4 565 486 027 761 ; б = 1 061 652 293 520 ; и с = 4 687 298 610 289 . Здесь а + b = 2 372 159 ² и с = 2 165 017 ² . Это генерируется по формуле Евклида со значениями параметров m = 2 150 905 и n = 246 792 .
• Существуют непримитивные треугольники Пифагора с целой высотой от гипотенузы . Такие треугольники Пифагора известны как разложимые, поскольку их можно разделить по этой высоте на два отдельных треугольника Пифагора меньшего размера.

Геометрия формулы Евклида

Рациональные точки на единичном круге

3,4,5 отображается в точку x,y (4/5,3/5) на единичном круге.

Рациональные точки окружности в стереографической проекции соответствуют рациональным точкам прямой.

Формула Евклида для тройки Пифагора.

$a=m^{2}-n^{2},\quad b=2mn,\quad c=m^{2}+n^{2}$

можно понять с точки зрения геометрии рациональных точек единичного круга ( Траутман, 1998 ).

Фактически, точка на декартовой плоскости с координатами ( x , y ) принадлежит единичному кругу, если x ² + и ² = 1 . Точка является рациональной, если x и y — рациональные числа , то есть если существуют взаимно простые целые числа a , b , c такие, что

${\biggl (}{\frac {a}{c}}{\biggr )}^{2}+{\biggl (}{\frac {b}{c}}{\biggr )}^{2}=1.$

Умножив оба члена на c ² , можно видеть, что рациональные точки на окружности находятся во взаимно однозначном соответствии с примитивными пифагорейскими тройками.

Единичный круг также может быть определен параметрическим уравнением

$x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.$

Формула Евклида для троек Пифагора и обратное соотношение t = y /( x + 1) означают, что, за исключением (−1, 0) , точка ( x , y ) на окружности является рациональной тогда и только тогда, когда соответствующее значение t — рациональное число. Обратите внимание, что t = y /( x + 1) = b /( a + c ) = n / m также является тангенсом половины угла , противоположного стороне треугольника длиной b .

Стереографический подход

Стереографическая проекция единичного круга на ось x . Дана точка P на единичной окружности, проведем линию от P до точки N = (0, 1) ( северный полюс ). Точка P ′, где линия пересекает ось x , является стереографической проекцией P . И наоборот, начиная с точки P ′ на оси x и рисуя линию от P ′ до N , обратная стереографическая проекция — это точка P , где линия пересекает единичный круг.

Существует соответствие между точками единичного круга с рациональными координатами и примитивными пифагорейскими тройками. На этом этапе формулы Евклида можно вывести либо методами тригонометрии , либо, что то же самое, с использованием стереографической проекции .

Для стереографического подхода предположим, что P ′ — точка на оси x с рациональными координатами.

$P'=\left({\frac {m}{n}},0\right).$

Тогда с помощью базовой алгебры можно показать, что точка P имеет координаты

$P=\left({\frac {2\left({\frac {m}{n}}\right)}{\left({\frac {m}{n}}\right)^{2}+1}},{\frac {\left({\frac {m}{n}}\right)^{2}-1}{\left({\frac {m}{n}}\right)^{2}+1}}\right)=\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right).$

Это устанавливает, что каждая рациональная точка оси x переходит в рациональную точку единичного круга. Обратное, что каждая рациональная точка единичного круга происходит из такой точки оси x , следует из применения обратной стереографической проекции. Предположим, что P ( x , y ) — точка единичного круга с рациональными числами x и y . Тогда точка P ′, полученная стереографической проекцией на ось x, имеет координаты

$\left({\frac {x}{1-y}},0\right)$

что рационально.

С точки зрения алгебраической геометрии , алгебраическое многообразие рациональных точек на единичной окружности бирационально аффинной прямой над рациональными числами. Таким образом, единичная окружность называется рациональной кривой , и именно этот факт обеспечивает явную параметризацию точек (рационального числа) на ней с помощью рациональных функций.

Треугольники Пифагора в двумерной решетке

Двумерная решетка — это регулярный массив изолированных точек, где, если какая-либо одна точка выбрана в качестве декартова начала координат (0, 0), то все остальные точки находятся в точках ( x , y ) , где x и y варьируются во всех положительных и отрицательных целых числах. . Любой треугольник Пифагора с тройкой ( a , b , c ) можно нарисовать внутри двумерной решетки с вершинами в координатах (0, 0) , ( a , 0) и (0, b ) . Количество точек решетки, лежащих строго внутри границ треугольника, определяется выражением ${\tfrac {(a-1)(b-1)-\gcd {(a,b)}+1}{2}};$ для примитивных пифагоровых троек это количество внутренней решетки равно ${\tfrac {(a-1)(b-1)}{2}}.$ Площадь (по теореме Пика равная на единицу меньше, чем количество внутренних решеток плюс половина количества граничных решеток) равна ${\tfrac {ab}{2}}$ .

Первое появление двух примитивных пифагорейских троек, имеющих одну и ту же площадь, происходит с треугольниками со сторонами (20, 21, 29), (12, 35, 37) и общей площадью 210 (последовательность A093536 в OEIS ). Первое появление двух примитивных троек Пифагора с одинаковым количеством внутренних решеток происходит с (18108, 252685, 253333), (28077, 162964, 165365) и количеством внутренних решеток 2287674594 (последовательность A225760 в OEIS ). Были обнаружены три примитивные тройки Пифагора, занимающие одну и ту же площадь: (4485, 5852, 7373) , (3059, 8580, 9109) , (1380, 19019, 19069) с площадью 13123110. На данный момент не существует набора из трех примитивных троек Пифагора. Было обнаружено, что у них одинаковое количество внутренних решеток.

Перечисление примитивных пифагорейских троек

По формуле Евклида все примитивные тройки Пифагора могут быть получены из целых чисел. $m$ и $n$ с $m>n>0$, $m+n$ странный и $\gcd(m,n)=1$. Следовательно, существует отображение 1 к 1 рациональных чисел (в самых низких терминах) в примитивные пифагоровы тройки, где ${\tfrac {n}{m}}$ находится в интервале $(0,1)$ и $m+n$ странный.

Обратное отображение примитивной тройки $(a,b,c)$ где $c>b>a>0$ к рациональному ${\tfrac {n}{m}}$ достигается путем изучения двух сумм $a+c$ и $b+c$. Одной из этих сумм будет квадрат, который можно приравнять $(m+n)^{2}$ а другой будет дважды квадратом, который можно приравнять к $2m^{2}$. Тогда можно определить рациональное ${\tfrac {n}{m}}$.

Чтобы перечислить примитивные пифагоровы тройки, рациональное можно выразить в виде упорядоченной пары. $(n,m)$ и отображается в целое число с помощью функции сопряжения, такой как функция сопряжения Кантора . Пример можно увидеть по адресу (последовательность A277557 в OEIS ). Это начинается

$8,18,19,32,33,34,\dots$ и дает обоснования

${\tfrac {1}{2}},{\tfrac {2}{3}},{\tfrac {1}{4}},{\tfrac {3}{4}},{\tfrac {2}{5}},{\tfrac {1}{6}},\dots$ они, в свою очередь, порождают примитивные тройки

$(3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),\dots$

Спиноры и модульная группа

Тройки Пифагора также могут быть закодированы в квадратную матрицу вида

$X={\begin{bmatrix}c+b&a\\a&c-b\end{bmatrix}}.$

Матрица такого вида симметрична . того, определитель X равен Кроме

$\det X=c^{2}-a^{2}-b^{2}\,$

который равен нулю именно тогда, когда ( a , b , c ) является тройкой Пифагора. Если X соответствует тройке Пифагора, то как матрица она должна иметь ранг 1.

Поскольку X симметрично, из результата линейной алгебры следует , что существует вектор-столбец ξ = [ m n ] ^Т так, что внешний продукт

$X=2{\begin{bmatrix}m\\n\end{bmatrix}}[m\ n]=2\xi \xi ^{T}\,$ ( 1 )

выполняется, где T обозначает транспонирование матрицы . Поскольку ξ и -ξ образуют одну и ту же тройку Пифагора, вектор ξ можно считать спинором (для группы Лоренца SO(1, 2)). Говоря абстрактно, формула Евклида означает, что каждая примитивная пифагорова тройка может быть записана как внешнее произведение спинора с целочисленными элементами на самого себя, как в ( 1 ).

Модульная группа Γ представляет собой набор матриц размера 2 × 2 с целыми элементами.

$A={\begin{bmatrix}\alpha &\beta \\\gamma &\delta \end{bmatrix}}$

с определителем, равным единице: αδ − βγ = 1 . Этот набор образует группу , поскольку обратная матрица из Γ снова находится в Γ, как и произведение двух матриц из Γ. Модульная группа действует на совокупности всех целочисленных спиноров. Более того, группа транзитивна на наборе целочисленных спиноров с относительно простыми элементами. Ибо если [ м н ] ^Т имеет относительно простые элементы, то

${\begin{bmatrix}m&-v\\n&u\end{bmatrix}}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}m\\n\end{bmatrix}}$

где u и v выбираются (по алгоритму Евклида ) так, что mu + nv = 1 .

Воздействуя на спинор ξ в ( 1 ), действие Γ переходит к действию на пифагоровы тройки, если учесть тройки с возможными отрицательными компонентами. Таким образом, если A — матрица из Γ , то

$2(A\xi )(A\xi )^{T}=AXA^{T}\,$ ( 2 )

приводит к действию на матрицу X в ( 1 ). Это не дает четко определенного действия над примитивными тройками, поскольку может превратить примитивную тройку в импримитивную. На этом этапе удобно (согласно Траутману 1998 ) называть тройку ( a , b , c ) стандартной , если c > 0 и либо ( a , b , c ) относительно просты, либо ( a /2, b /2, c /2) относительно простые с нечетным /2 . Если спинор [ m n ] ^Т имеет относительно простые элементы, то соответствующая тройка ( a , b , c ) , определяемая ( 1 ), является стандартной тройкой. Отсюда следует, что действие модулярной группы транзитивно на множестве стандартных троек.

Альтернативно, ограничьте внимание теми значениями m и n, для которых m нечетно, а n четно. Пусть подгруппа Γ(2) группы Γ является ядром группового гомоморфизма

$\Gamma =\mathrm {SL} (2,\mathbf {Z} )\to \mathrm {SL} (2,\mathbf {Z} _{2})$

где SL(2, Z2 _по ) — специальная линейная группа над конечным полем Z2 _чисел целых модулю 2 . Тогда Γ(2) — группа унимодулярных преобразований, сохраняющих четность каждого элемента. Таким образом, если первая запись ξ нечетная, а вторая четная, то то же самое верно и для A ξ для всех A ∈ Γ(2) . Фактически, под действием ( 2 ) группа Γ(2) действует транзитивно на наборе примитивных пифагоровых троек ( Альперин 2005 ).

Группа Γ(2) — это свободная группа , генераторами которой являются матрицы

$U={\begin{bmatrix}1&2\\0&1\end{bmatrix}},\qquad L={\begin{bmatrix}1&0\\2&1\end{bmatrix}}.$

Следовательно, каждая примитивная пифагорова тройка может быть получена единственным способом как произведение копий матриц U и L .

Родительско-детские отношения

Основная статья: Дерево троек Пифагора

По результату Берггрена (1934) все примитивные пифагоровы тройки могут быть созданы из треугольника (3, 4, 5) с помощью трех линейных преобразований T ₁ , T ₂ , T ₃ ниже, где a , b , c — стороны из тройки:

	новая сторона а	новая сторона б	новая сторона с
Т 1 :	а - 2 б + 2 с	2а − б + 2в	2а − 2б + 3в
Т 2 :	а + 2 б + 2 в	2а + б + 2в	2а + 2б + 3в
Т3 :	− а + 2 б + 2 с	−2 а + б + 2 с	−2 а + 2 б + 3 с

Другими словами, каждая примитивная тройка будет «родителем» для трех дополнительных примитивных троек.Начиная с начального узла с a = 3 , b = 4 и c = 5 , операция T ₁ создает новую тройку

(3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),

и аналогично T ₂ и T ₃ образуют тройки (21, 20, 29) и (15, 8, 17).

Линейные преобразования Т1 _, Т2 _и Т3 _имеют геометрическую интерпретацию на языке квадратичных форм . Они тесно связаны (но не равны) с отражениями, порождающими ортогональную группу x ² + и ² - г ² над целыми числами.

Связь с целыми гауссовыми числами

Альтернативно, формулы Евклида можно проанализировать и доказать, используя целые числа Гаусса . Гауссовы целые числа — это комплексные числа вида α = u + vi , где u и v — обычные целые числа , а i — квадратный корень из отрицательного . Единицами . гауссовских целых чисел являются ±1 и ±i Обычные целые числа называются рациональными целыми числами и обозначаются буквой « Z ». Гауссовы целые числа обозначаются как Z [ i ] . Правую часть теоремы Пифагора можно разложить на целые гауссовы числа:

$c^{2}=a^{2}+b^{2}=(a+bi){\overline {(a+bi)}}=(a+bi)(a-bi).$

Примитивная тройка Пифагора — это тройка, в которой a и b , взаимно просты т. е. у них нет общих простых делителей в целых числах. Для такой тройки либо a , либо b четное, а другое нечетное; отсюда следует, что c также нечетно.

Каждый из двух множителей z := a + bi и z* := a − bi примитивной пифагоровой тройки равен квадрату гауссового целого числа. Это можно доказать, используя свойство, согласно которому каждое гауссово целое число можно однозначно разложить на гауссовы простые числа с точностью до единиц . (Эта уникальная факторизация следует из того, что, грубо говоря, на них можно определить версию алгоритма Евклида .) Доказательство состоит из трех шагов. Во-первых, если a и b не имеют общих простых множителей в целых числах, то они также не имеют общих простых множителей в целых гауссовых числах. (Предположим, a = gu и b = gv с целыми гауссовыми числами g , u и v и g не единицей. Тогда u и v лежат на одной прямой, проходящей через начало координат. Все гауссовские целые числа на такой линии являются целыми числами, кратными некоторому гауссовскому целому числу. h , Но тогда целое число gh ≠ ±1 делит и a, и b .) Во-вторых, из этого следует, что z и z* также не имеют общих простых делителей в гауссовских целых числах. Ведь если бы они это сделали, то их общий делитель δ также делил бы z + z* = 2 a и z − z* = 2 ib . Поскольку a и b взаимно просты, это означает, что δ делит 2 = (1 + i)(1 - i) = i(1 - i) ² . Из формулы с ² = zz* , что, в свою очередь, означало бы, что c четно, что противоречит гипотезе примитивной пифагоровой тройки. В-третьих, поскольку c ² является квадратом, каждое гауссово простое число при его факторизации удваивается, т. е. появляется четное число раз. Поскольку у z и z* нет общих простых делителей, это удвоение справедливо и для них. Следовательно, z и z* — квадраты.

Таким образом, первый фактор можно записать

$a+bi=\varepsilon \left(m+ni\right)^{2},\quad \varepsilon \in \{\pm 1,\pm i\}.$

Действительная и мнимая части этого уравнения дают две формулы:

${\begin{cases}\varepsilon =+1,&\quad a=+\left(m^{2}-n^{2}\right),\quad b=+2mn;\\\varepsilon =-1,&\quad a=-\left(m^{2}-n^{2}\right),\quad b=-2mn;\\\varepsilon =+i,&\quad a=-2mn,\quad b=+\left(m^{2}-n^{2}\right);\\\varepsilon =-i,&\quad a=+2mn,\quad b=-\left(m^{2}-n^{2}\right).\end{cases}}$

Для любой примитивной тройки Пифагора должны существовать целые числа m и n, такие, что эти два уравнения удовлетворяются. Следовательно, каждая пифагорова тройка может быть получена из некоторого выбора этих целых чисел.

Как идеальные квадратные гауссовы целые числа

Если мы рассмотрим квадрат гауссовского целого числа, мы получим следующую прямую интерпретацию формулы Евклида как представления идеального квадрата гауссовского целого числа.

$(m+ni)^{2}=(m^{2}-n^{2})+2mni.$

Используя тот факт, что гауссовы целые числа являются евклидовой областью, а для гауссовского целого числа p $|p|^{2}$ всегда является квадратом, можно показать, что пифагорова тройка соответствует квадрату простого гауссовского целого числа, если гипотенуза проста.

Если целое число Гаусса не является простым, то оно является произведением двух целых чисел Гаусса p и q с $|p|^{2}$ и $|q|^{2}$ целые числа. Поскольку величины умножаются на целые гауссовы числа, произведение должно быть $|p||q|$, которое при возведении в квадрат для нахождения пифагоровой тройки должно быть составным. Противоположение завершает доказательство.

Распределение троек

Диаграмма рассеяния ножек ( a , b ) первых пифагорейских троек с a и b меньше 4500.

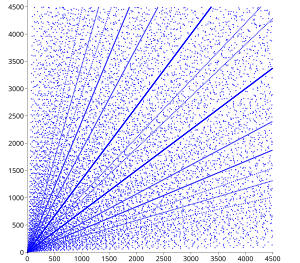
Имеется ряд результатов о распределении пифагоровых троек. На диаграмме рассеяния уже виден ряд очевидных закономерностей. ножки ( a , b ) Всякий раз, когда на графике появляются примитивной тройки, на графике также должны появиться все целые числа, кратные ( a , b ) , и это свойство приводит к появлению линий, исходящих от начала координат на диаграмме.

Внутри разброса находятся наборы параболических паттернов с высокой плотностью точек и всеми их фокусами в начале координат, раскрывающимися во всех четырех направлениях. Различные параболы пересекаются по осям и, кажется, отражаются от оси под углом падения 45 градусов, при этом третья парабола входит перпендикулярно. Внутри этого квадранта каждая дуга с центром в начале координат показывает ту часть параболы, которая лежит между ее вершиной и пересечением с полураскрытой прямой кишкой .

Эти закономерности можно объяснить следующим образом. Если $a^{2}/4n$ является целым числом, тогда ( a , $|n-a^{2}/4n|$, $n+a^{2}/4n$) — пифагорова тройка. (Фактически, каждую пифагорову тройку ( a , b , c ) можно записать таким образом с целым числом n , возможно, после замены a и b , поскольку $n=(b+c)/2$ и a и b не могут быть одновременно нечетными.) Таким образом, пифагоровы тройки лежат на кривых, заданных формулой $b=|n-a^{2}/4n|$, то есть параболы, отраженные от оси a , и соответствующие кривые с a и b поменялись местами. Если a варьируется для данного n (т.е. по данной параболе), целые значения b встречаются относительно часто, если n является квадратом или небольшим кратным квадрату. Если несколько таких значений лежат близко друг к другу, соответствующие параболы примерно совпадают, и тройки группируются в узкую параболическую полосу. Например, 38 ² = 1444 , 2 × 27 ² = 1458 , 3 × 22 ² = 1452 , 5 × 17 ² = 1445 и 10 × 12 ² = 1440 ; соответствующая параболическая полоса в районе n ≈ 1450 на диаграмме рассеяния хорошо видна .

Описанные выше угловые свойства непосредственно следуют из функциональной формы парабол. Параболы отражаются от оси a при a = 2 n , а производная b по a в этой точке равна –1; следовательно, угол падения равен 45°. Поскольку кластеры, как и все тройки, повторяются с целыми числами, кратными целым числам, значение 2 n также соответствует кластеру. Соответствующая парабола пересекает ось b под прямым углом при b = 2 n , и, следовательно, ее отражение при перестановке a и b пересекает ось a под прямым углом при a = 2 n , именно там, где парабола для n отражается при ось а . (То же самое, конечно, справедливо и для поменянных местами a и b .)

Альберт Фесслер и другие дают представление о значении этих парабол в контексте конформных отображений.

Особые случаи и связанные с ними уравнения

Платоническая последовательность

Случай n = 1 более общей конструкции пифагоровых троек известен давно. Прокл в своем комментарии к 47-му положению первой книги « » Евклида Начал описывает его следующим образом:

Некоторые методы открытия треугольников такого рода передаются из поколения в поколение, один из которых они отсылают к Платону, а другой к Пифагору . (Последний) начинается с нечетных чисел. Ибо оно делает нечетное число меньшей из сторон прямого угла; затем он берет его квадрат, вычитает единицу и делает половину разницы большей из сторон прямого угла; наконец, оно добавляет к этому единицу и образует, таким образом, оставшуюся сторону — гипотенузу.
...Ибо метод Платона рассуждает четными числами. Он берет заданное четное число и делает его одной из сторон под прямым углом; затем, разделив это число пополам и возведя половину в квадрат, он прибавляет единицу к квадрату, чтобы образовать гипотенузу, и вычитает единицу из квадрата, чтобы образовать другую сторону вокруг прямого угла. ... Таким образом образовался тот же треугольник, что и получен другим методом.

В форме уравнения это выглядит так:

а нечетно (Пифагор, ок. 540 г. до н. э.):

${\text{side }}a:{\text{side }}b={a^{2}-1 \over 2}:{\text{side }}c={a^{2}+1 \over 2}.$

а четно (Платон, ок. 380 г. до н. э.):

${\text{side }}a:{\text{side }}b=\left({a \over 2}\right)^{2}-1:{\text{side }}c=\left({a \over 2}\right)^{2}+1$

Можно показать, что все пифагоровы тройки могут быть получены с соответствующим изменением масштаба из основной платоновской последовательности ( a , ( a ² − 1)/2 и ( а ² + 1)/2 ), позволяя a принимать нецелочисленные рациональные значения. Если в последовательности a заменить на дробь m / n , результат будет равен «стандартному» тройному генератору (2 mn , m ² − п ² , м ² + н ² ) после изменения масштаба. Отсюда следует, что каждой тройке соответствует рациональное значение a , которое можно использовать для создания подобного треугольника (с теми же тремя углами и сторонами в тех же пропорциях, что и исходный). Например, платоновский эквивалент (56, 33, 65) генерируется формулой a = m / n = 7/4 как ( a , ( a ² –1)/2, ( а ² +1)/2) = (56/32, 33/32, 65/32) . Саму платоновскую последовательность можно вывести следуя шагам «разделения квадрата», описанным у Диофанта II.VIII .

Уравнение Якоби–Мэддена

Основная статья: уравнение Якоби – Мэддена

Уравнение,

$a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}$

эквивалентно специальной тройке Пифагора,

$(a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=((a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}$

Существует бесконечное количество решений этого уравнения, поскольку для решения переменных используется эллиптическая кривая . Маленькие такие,

$a,b,c,d=-2634,955,1770,5400$

$a,b,c,d=-31764,7590,27385,48150$

Равные суммы двух квадратов

Один из способов найти решения для $a^{2}+b^{2}=c^{2}+d^{2}$ заключается в параметризации a, b, c, d целыми числами m, n, p, q следующим образом:

$(m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}.$

Равные суммы двух четвертых степеней

Даны два набора троек Пифагора.

$(a^{2}-b^{2})^{2}+(2ab)^{2}=(a^{2}+b^{2})^{2}$

$(c^{2}-d^{2})^{2}+(2cd)^{2}=(c^{2}+d^{2})^{2}$

задача о нахождении равных произведений негипотенузной стороны и гипотенузы,

$(a^{2}-b^{2})(a^{2}+b^{2})=(c^{2}-d^{2})(c^{2}+d^{2})$

Легко видеть, что это эквивалентно уравнению

$a^{4}-b^{4}=c^{4}-d^{4}$

и впервые был решен Эйлером как $a,b,c,d=133,59,158,134$. Поскольку он показал, что это рациональная точка эллиптической кривой , то существует бесконечное количество решений. Фактически, он также нашел параметризацию полинома 7-й степени.

Теорема Декарта о круге

В случае теоремы Декарта о круге , когда все переменные являются квадратами,

$2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2})^{2}$

Эйлер показал, что это эквивалентно трем одновременным тройкам Пифагора:

$(2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})^{2}$

$(2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})^{2}$

$(2ad)^{2}+(2bc)^{2}=(a^{2}-b^{2}-c^{2}+d^{2})^{2}$

Существует также бесконечное число решений, и для частного случая, когда $a+b=c$, то уравнение упрощается до

$4(a^{2}+ab+b^{2})=d^{2}$

с небольшими решениями, такими как $a,b,c,d=3,5,8,14$ и может быть решена как двоичные квадратичные формы .

Почти равнобедренные пифагоровы тройки

Ни одна пифагорова тройка не является равнобедренной , поскольку отношение гипотенузы к любой другой стороне равно √ 2 , но √ 2 не может быть выражено как отношение двух целых чисел .

Однако существуют прямоугольные треугольники с целыми сторонами, у которых длины сторон, не являющихся гипотенузами, отличаются на единицу, например:

$3^{2}+4^{2}=5^{2}$

$20^{2}+21^{2}=29^{2}$

и бесконечное количество других. Они могут быть полностью параметризованы как:

$\left({\tfrac {x-1}{2}}\right)^{2}+\left({\tfrac {x+1}{2}}\right)^{2}=y^{2}$

где { x, y } — решения уравнения Пелля $x^{2}-2y^{2}=-1$.

Если a , b , c являются сторонами этого типа примитивной тройки Пифагора, то решение уравнения Пелля дается рекурсивной формулой

$a_{n}=6a_{n-1}-a_{n-2}+2$ с $a_{1}=3$ и $a_{2}=20$

$b_{n}=6b_{n-1}-b_{n-2}-2$ с $b_{1}=4$ и $b_{2}=21$

$c_{n}=6c_{n-1}-c_{n-2}$ с $c_{1}=5$ и $c_{2}=29$.

Эта последовательность примитивных пифагоровых троек образует центральный ствол (ствол) корневого троичного дерева примитивных пифагоровых троек.

Когда более длинная сторона, не являющаяся гипотенузой, и гипотенуза отличаются на единицу, например, в

$5^{2}+12^{2}=13^{2}$

$7^{2}+24^{2}=25^{2}$

тогда полное решение примитивной пифагоровой тройки a , b , c будет

$a=2m+1,\quad b=2m^{2}+2m,\quad c=2m^{2}+2m+1$

и

$(2m+1)^{2}+(2m^{2}+2m)^{2}=(2m^{2}+2m+1)^{2}$

где целое число $m>0$ является генерирующим параметром.

Это показывает, что все нечетные числа (больше 1) встречаются в этом типе почти равнобедренной примитивной пифагоровой тройки. Эта последовательность примитивных пифагоровых троек образует правый внешний ствол корневого троичного дерева примитивных пифагоровых троек.

Другое свойство этого типа почти равнобедренной примитивной пифагоровой тройки состоит в том, что стороны связаны так, что

$a^{b}+b^{a}=Kc$

для некоторого целого числа $K$. Или другими словами $a^{b}+b^{a}$ делится на $c$ например, в

$(5^{12}+12^{5})/13=18799189$.

Числа Фибоначчи в тройках Пифагора

Начиная с 5, каждое второе число Фибоначчи — это длина гипотенузы прямоугольного треугольника с целыми сторонами, или другими словами, наибольшее число в пифагоровой тройке, полученное по формуле $$(F_{n}F_{n+3})^{2}+(2F_{n+1}F_{n+2})^{2}=F_{2n+3}^{2}.$$Последовательность треугольников Пифагора, полученная по этой формуле, имеет стороны длины

(3,4,5), (5,12,13), (16,30,34), (39,80,89), ...

Средняя сторона каждого из этих треугольников представляет собой сумму трёх сторон предыдущего треугольника.

Обобщения

Существует несколько способов обобщить понятие пифагорейских троек.

Пифагорейский n -кортеж

Смотрите также: четверка Пифагора

Выражение

$\left(m_{1}^{2}-m_{2}^{2}-\ldots -m_{n}^{2}\right)^{2}+\sum _{k=2}^{n}(2m_{1}m_{k})^{2}=\left(m_{1}^{2}+\ldots +m_{n}^{2}\right)^{2}$

является пифагорейским n -кортежом для любого набора натуральных чисел ( m ₁ , ..., m _n ) с m ²
₁ > м ²
₂ +...+ м ²
_н . Пифагорейский набор n можно сделать примитивным, разделив его значения на наибольший общий делитель.

Более того, любой примитивный пифагоров n -кортеж a ²
₁ +...+ а ²
_п = с ² можно найти с помощью этого подхода. Используйте ( m ₁ , ..., m _n ) = ( c + a ₁ , a ₂ , ..., an _n ), чтобы получить пифагорейский n -кортеж по приведенной выше формуле и разделите его на наибольший общий целочисленный делитель, что составляет 2 м ₁ знак равно 2( c + а ₁ ) . Деление на наибольший общий делитель этих ( m ₁ , ..., m _n ) значений дает тот же самый примитивный пифагорейский n -кортеж; и существует взаимно однозначное соответствие между кортежами взаимно простых положительных целых чисел ( m ₁ , ..., m _n ), удовлетворяющих m ²
₁ > м ²
₂ +...+ м ²
_n и примитивные пифагорейские n -кортежи.

Примеры связи между взаимно простыми значениями ${\vec {m}}$ и примитивные пифагорейские n -кортежи включают:

${\begin{aligned}{\vec {m}}=(1)&\leftrightarrow 1^{2}=1^{2}\\{\vec {m}}=(2,1)&\leftrightarrow 3^{2}+4^{2}=5^{2}\\{\vec {m}}=(2,1,1)&\leftrightarrow 1^{2}+2^{2}+2^{2}=3^{2}\\{\vec {m}}=(3,1,1,1)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}=2^{2}\\{\vec {m}}=(5,1,1,2,3)&\leftrightarrow 1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}\\{\vec {m}}=(4,1,1,1,1,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+1^{2}+2^{2}=3^{2}\\{\vec {m}}=(5,1,1,1,2,2,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+2^{2}+2^{2}+2^{2}=4^{2}\end{aligned}}$

Последовательные квадраты

Поскольку сумма F ( k , m ) k последовательных квадратов , начинающихся с m ² задается формулой,

$F(k,m)=km(k-1+m)+{\frac {k(k-1)(2k-1)}{6}}$

можно найти значения ( k , m ) так, что F ( k , m ) является квадратом, например квадратом Хиршхорна, где количество терминов само по себе является квадратом,

$m={\tfrac {v^{4}-24v^{2}-25}{48}},\;k=v^{2},\;F(m,k)={\tfrac {v^{5}+47v}{48}}$

и v ≥ 5 — любое целое число, не кратное 2 или 3. Для наименьшего случая v = 5 , следовательно, k = 25 , это дает хорошо известную задачу Лукаса о укладке пушечных ядер :

$0^{2}+1^{2}+2^{2}+\dots +24^{2}=70^{2}$

факт, который связан с решеткой Лича .

Кроме того, если в пифагоровом n -кортеже ( n ≥ 4 ) все сложения последовательные, кроме одного, можно использовать уравнение

$F(k,m)+p^{2}=(p+1)^{2}$

Поскольку вторая степень p сокращается, это линейно и легко решается как $p={\tfrac {F(k,m)-1}{2}}$ хотя k , m следует выбирать так, чтобы p было целым числом, небольшим примером является k = 5 , m = 1 , что дает:

$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+27^{2}=28^{2}$

один из способов генерации пифагорейских n -кортежей состоит в использовании для различных x Таким образом ,

$x^{2}+(x+1)^{2}+\cdots +(x+q)^{2}+p^{2}=(p+1)^{2},$

где q = n –2 и где

$p={\frac {(q+1)x^{2}+q(q+1)x+{\frac {q(q+1)(2q+1)}{6}}-1}{2}}.$

Последняя теорема Ферма

Основная статья: Последняя теорема Ферма

Обобщением понятия троек Пифагора является поиск троек натуральных чисел a , b и c , таких, что a ^н + б ^н = с ^н , для некоторого n строго большего 2. Пьер де Ферма в 1637 году утверждал, что такой тройки не существует, и это утверждение стало известно как Великая теорема Ферма, потому что для его доказательства или опровержения потребовалось больше времени, чем для любой другой гипотезы Ферма. Первое доказательство было дано Эндрю Уайлсом в 1994 году.

n - 1 или n n -й степени, сумма которых равна n-й степени

Основная статья: Гипотеза Эйлера о сумме степеней

Другое обобщение - это поиск последовательностей из n + 1 положительных целых чисел, для которых n- я степень последнего является суммой n- й степени предыдущих членов. Наименьшие последовательности для известных значений n :

• п = 3: {3, 4, 5; 6}.
• п = 4: {30, 120, 272, 315; 353}
• п = 5: {19, 43, 46, 47, 67; 72}
• п = 7: {127, 258, 266, 413, 430, 439, 525; 568}
• п = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}

Для случая n = 3 , когда $x^{3}+y^{3}+z^{3}=w^{3},$ называемая кубикой Ферма , существует общая формула, дающая все решения.

Немного другое обобщение позволяет сумме ( k + 1) n- й степени равняться сумме ( n - k ) n- й степени. Например:

• ( п = 3 ): 1 ³ + 12 ³ = 9 ³ + 10 ³ , прославившийся благодаря воспоминаниям Харди о разговоре с Рамануджаном о том, что число 1729 — это наименьшее число, которое можно выразить в виде суммы двух кубов двумя разными способами.

Также могут существовать n - 1 положительные целые числа, сумма n- х степеней которых равна n- й степени (хотя, согласно Великой теореме Ферма , не для n = 3) ; это контрпримеры к гипотезе Эйлера о сумме степеней . Наименьшими известными контрпримерами являются

• n = 4 : (95800, 217519, 414560; 422481)
• n = 5 : (27, 84, 110, 133; 144)

Тройки геронова треугольника

Основная статья: Геронов треугольник

Геронов треугольник обычно определяется как треугольник с целыми сторонами, площадь которого также является целым числом. Длины сторон такого треугольника образуют тройку Герона ( a, b, c ) при a ≤ b ≤ c .Каждая тройка Пифагора является тройкой Герона, поскольку хотя бы одна из ног a , b должна быть четной в тройке Пифагора, поэтому площадь ab /2 является целым числом. Однако не каждая тройка Герона является тройкой Пифагора, как показывает пример (4, 13, 15) с площадью 24.

Если ( a , b , c ) — тройка Герона, то же самое относится и к ( ka , kb , kc ) , где k — любое положительное целое число; его площадь будет целым числом, равным k ² умножить на целую площадь треугольника ( a , b , c ) .Геронова тройка ( a , b , c ) является примитивной при условии, что a , b , c просты взаимно . (К примитивным пифагоровым тройкам также применимо более строгое утверждение о том, что они попарно взаимно просты, но к примитивным героновым треугольникам более сильное утверждение не всегда справедливо, как, например, в случае (7, 15, 20) .) Вот несколько простейших примитивных треугольников. Героновы тройки, не являющиеся тройками Пифагора:

(4, 13, 15) площадью 24

(3, 25, 26) площадью 36

(7, 15, 20) площадью 42

(6, 25, 29) площадью 60

(11, 13, 20) площадью 66

(13, 14, 15) площадью 84

(13, 20, 21) площадью 126

По формуле Герона дополнительным условием для того, чтобы тройка натуральных чисел ( a , b , c ) с a < b < c была героновой, является то, что

( а ² + б ² + с ² ) ² − 2( а ⁴ + б ⁴ + с ⁴ )

или эквивалентно

2( а ² б ² + а ² с ² + б ² с ² ) − ( а ⁴ + б ⁴ + с ⁴ )

быть ненулевым полным квадратом, делящимся на 16.

Приложение к криптографии

Примитивные тройки Пифагора использовались в криптографии в качестве случайных последовательностей и для генерации ключей.

См. также

• Булева задача о тройках Пифагора
• Треугольник Брахмагупты
• Конгруэнтный
• Диофант II.VIII
• тройка Эйзенштейна
• Эйлеров кирпич
• Геронов треугольник
• Теорема Гильберта 90
• Целочисленный треугольник
• Модульная арифметика
• Негипотенузное число
• Плимптон 322
• Пифагорово простое число
• Пифагорова четверка
• Квадрик
• Формула касательного полуугла
• Тригонометрическое тождество

Ссылки

• Альперин, Роджер К. (2005), «Модульное дерево Пифагора» (PDF) , American Mathematical Monthly , 112 (9): 807–816, CiteSeerX   10.1.1.112.3085 , doi : 10.2307/30037602 , JSTOR   30037602 , MR   2179860
• Берггрен, Б. (1934), «Треугольники Пифагора», Журнал элементарной математики, физики и химии (на шведском языке), 17 : 129–139.
• Барнинг, FJM (1963), «О пифагоровых и околопифагоровых треугольниках и процессе генерации с использованием унимодулярных матриц» (PDF) , Math. Центр Амстердама Отдел. Чистая математика. (на голландском языке), ZW-011: 37
• Эккерт, Эрнест (1992), «Примитивные пифагоровы тройки», The College Mathematics Journal , 23 (5): 413–417, doi : 10.2307/2686417 , JSTOR   2686417
• Элкис, Ноам , тройки Пифагора и теорема Гильберта 90 (PDF)
• Хит, Томас (1956), Тринадцать книг «Элементов Евклида», том. 1 (Книги I и II) (2-е изд.), Dover Publications, ISBN  978-0-486-60088-8
• Лонг, Кэлвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Лексингтон: DC Heath and Company , LCCN   77171950
• Мартин, Артемас (1875), «Рациональные прямоугольные треугольники, почти равнобедренные», The Analyst , 3 (2): 47–50, doi : 10.2307/2635906 , JSTOR   2635906
• Маккалоу, Дэррил (2005), «Высота и превышение троек Пифагора» (PDF) , Mathematics Magazine , 78 (1): 26–44, doi : 10.1080/0025570X.2005.11953298 , S2CID   1701449
• Ромик, Дэн (2008), «Динамика пифагорейских троек» (PDF) , Пер. амер. Математика. Соц. , 360 (11): 6045–6064, arXiv : math.DS/0406512 , doi : 10.1090/S0002-9947-08-04467-X , MR   2425702
• Тейген, МГ; Хэдвин, Д. У. (1971), «О создании троек Пифагора», The American Mathematical Monthly , 78 (4): 378–379, doi : 10.2307/2316903 , JSTOR   2316903
• Траутман, Анджей (1998), «Пифагорейские спиноры и твисторы Пенроуза» , в SA Hugget; Эл Джей Мейсон; КП Тод; СТ Цоу; NMJ Вудхаус (ред.), Геометрическая вселенная (Постскриптум)

Внешние ссылки

• Алгебры Клиффорда и параметризация Евклида пифагоровых троек
• Любопытные последствия неправильно скопированного квадратичного уравнения
• Обсуждение свойств троек Пифагора, интерактивных калькуляторов, головоломок и задач.
• Генерация троек Пифагора с использованием арифметических прогрессий
• «Числа Пифагора» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Интерактивный калькулятор троек Пифагора
• Отрицательное уравнение Пелля и тройки Пифагора
• Параметризация троек Пифагора одной тройкой многочленов
• Прайс, Х. Ли (2008), Дерево Пифагора: новый вид , arXiv : 0809.4324
• Пифагоровы тройки и единичный круг , гл. 2–3, в книге Джозефа Х. Сильвермана « Дружеское введение в теорию чисел », 3-е изд., 2006 г., Пирсон Прентис Холл, Аппер-Сэддл-Ривер, Нью-Джерси, ISBN   0-13-186137-9
• Пифагоровы тройки в интерактивном апплете , показывающем взаимосвязь единичного круга с пифагорейскими тройками
• Пифагорейские тройки
• Замечательная вписанная окружность треугольника
• Решения квадратично-совместимых пар относительно пифагоровых троек
• Теоретические свойства троек Пифагора и связь с геометрией.
• Троичное дерево(я), лежащее в основе примитивных пифагорейских троек, при разрезании узла
• Вайсштейн, Эрик В. , «Тройка Пифагора» , MathWorld