Equalities that involve trigonometric functions
В тригонометрии , тригонометрические тождества — это равенства , которые включают тригонометрические функции и верны для любого значения встречающихся переменных для которых определены обе части равенства. Геометрически это тождества, включающие в себя определенные функции одного или нескольких углов . Они отличаются от тождеств треугольника , которые потенциально включают в себя углы, но также включают длины сторон или другие длины треугольника .
Эти тождества полезны всякий раз, когда необходимо упростить выражения, включающие тригонометрические функции. Важным применением является интегрирование нетригонометрических функций: общий метод предполагает сначала использование правила замены тригонометрической функцией , а затем упрощение полученного интеграла с помощью тригонометрического тождества.
Тригонометрические функции и обратные им на единичной окружности. Все прямоугольные треугольники подобны, то есть соотношения между соответствующими сторонами одинаковы. Для sin, cos и tan радиус единичной длины образует гипотенузу определяющего их треугольника. Взаимные тождества возникают как отношения сторон в треугольниках, где эта единичная линия больше не является гипотенузой. Треугольник, закрашенный синим цветом, иллюстрирует идентичность. 1 + cot 2 θ = csc 2 θ {\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta } tan 2 θ + 1 = sec 2 θ {\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta } Основное соотношение между синусом и косинусом задается тождеством Пифагора:
sin 2 θ + cos 2 θ = 1 , {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}
где sin 2 θ {\displaystyle \sin ^{2}\theta } ( sin θ ) 2 {\displaystyle (\sin \theta )^{2}} cos 2 θ {\displaystyle \cos ^{2}\theta } ( cos θ ) 2 . {\displaystyle (\cos \theta )^{2}.}
Это можно рассматривать как версию теоремы Пифагора и следует из уравнения x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} единичного круга . Это уравнение можно решить как для синуса, так и для косинуса:
sin θ = ± 1 − cos 2 θ , cos θ = ± 1 − sin 2 θ . {\displaystyle {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta }},\\\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta }}.\end{aligned}}}
где знак зависит квадранта от θ . {\displaystyle \theta .}
Разделив это тождество на sin 2 θ {\displaystyle \sin ^{2}\theta } cos 2 θ {\displaystyle \cos ^{2}\theta } 1 + cot 2 θ = csc 2 θ 1 + tan 2 θ = sec 2 θ sec 2 θ + csc 2 θ = sec 2 θ csc 2 θ {\displaystyle {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \\&1+\tan ^{2}\theta =\sec ^{2}\theta \\&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}}
Используя эти тождества, можно выразить любую тригонометрическую функцию через любую другую ( с точностью до знака плюс или минус):
Каждая тригонометрическая функция через каждую из пяти остальных. [1] с точки зрения sin θ {\displaystyle \sin \theta } csc θ {\displaystyle \csc \theta } cos θ {\displaystyle \cos \theta } sec θ {\displaystyle \sec \theta } tan θ {\displaystyle \tan \theta } cot θ {\displaystyle \cot \theta } sin θ = {\displaystyle \sin \theta =} sin θ {\displaystyle \sin \theta } 1 csc θ {\displaystyle {\frac {1}{\csc \theta }}} ± 1 − cos 2 θ {\displaystyle \pm {\sqrt {1-\cos ^{2}\theta }}} ± sec 2 θ − 1 sec θ {\displaystyle \pm {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}} ± tan θ 1 + tan 2 θ {\displaystyle \pm {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}} ± 1 1 + cot 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}} csc θ = {\displaystyle \csc \theta =} 1 sin θ {\displaystyle {\frac {1}{\sin \theta }}} csc θ {\displaystyle \csc \theta } ± 1 1 − cos 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}} ± sec θ sec 2 θ − 1 {\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}} ± 1 + tan 2 θ tan θ {\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}} ± 1 + cot 2 θ {\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}} cos θ = {\displaystyle \cos \theta =} ± 1 − sin 2 θ {\displaystyle \pm {\sqrt {1-\sin ^{2}\theta }}} ± csc 2 θ − 1 csc θ {\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}} cos θ {\displaystyle \cos \theta } 1 sec θ {\displaystyle {\frac {1}{\sec \theta }}} ± 1 1 + tan 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}} ± cot θ 1 + cot 2 θ {\displaystyle \pm {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}} sec θ = {\displaystyle \sec \theta =} ± 1 1 − sin 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\sin ^{2}\theta }}}} ± csc θ csc 2 θ − 1 {\displaystyle \pm {\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}} 1 cos θ {\displaystyle {\frac {1}{\cos \theta }}} sec θ {\displaystyle \sec \theta } ± 1 + tan 2 θ {\displaystyle \pm {\sqrt {1+\tan ^{2}\theta }}} ± 1 + cot 2 θ cot θ {\displaystyle \pm {\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}} tan θ = {\displaystyle \tan \theta =} ± sin θ 1 − sin 2 θ {\displaystyle \pm {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}} ± 1 csc 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}} ± 1 − cos 2 θ cos θ {\displaystyle \pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}} ± sec 2 θ − 1 {\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}}} tan θ {\displaystyle \tan \theta } 1 cot θ {\displaystyle {\frac {1}{\cot \theta }}} cot θ = {\displaystyle \cot \theta =} ± 1 − sin 2 θ sin θ {\displaystyle \pm {\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}} ± csc 2 θ − 1 {\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}}} ± cos θ 1 − cos 2 θ {\displaystyle \pm {\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}} ± 1 sec 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\sec ^{2}\theta -1}}}} 1 tan θ {\displaystyle {\frac {1}{\tan \theta }}} cot θ {\displaystyle \cot \theta }
Исследуя единичную окружность, можно установить следующие свойства тригонометрических функций.
Преобразование координат ( a , b ) при сдвиге угла отражения α {\displaystyle \alpha } π 4 {\displaystyle {\frac {\pi }{4}}} Когда направление евклидова вектора представлено углом θ , {\displaystyle \theta ,} x {\displaystyle x} x {\displaystyle x} θ {\displaystyle \theta } α , {\displaystyle \alpha ,} θ ′ {\displaystyle \theta ^{\prime }} θ ′ = 2 α − θ . {\displaystyle \theta ^{\prime }=2\alpha -\theta .}
Значения тригонометрических функций этих углов θ , θ ′ {\displaystyle \theta ,\;\theta ^{\prime }} α {\displaystyle \alpha } формулы приведения . [2]
θ {\displaystyle \theta } α = 0 {\displaystyle \alpha =0} [3] нечетные/четные тождества θ {\displaystyle \theta } α = π 4 {\displaystyle \alpha ={\frac {\pi }{4}}} θ {\displaystyle \theta } α = π 2 {\displaystyle \alpha ={\frac {\pi }{2}}} θ {\displaystyle \theta } α = 3 π 4 {\displaystyle \alpha ={\frac {3\pi }{4}}} θ {\displaystyle \theta } α = π {\displaystyle \alpha =\pi } сравнить с α = 0 {\displaystyle \alpha =0} sin ( − θ ) = − sin θ {\displaystyle \sin(-\theta )=-\sin \theta } sin ( π 2 − θ ) = cos θ {\displaystyle \sin \left({\tfrac {\pi }{2}}-\theta \right)=\cos \theta } sin ( π − θ ) = + sin θ {\displaystyle \sin(\pi -\theta )=+\sin \theta } sin ( 3 π 2 − θ ) = − cos θ {\displaystyle \sin \left({\tfrac {3\pi }{2}}-\theta \right)=-\cos \theta } sin ( 2 π − θ ) = − sin ( θ ) = sin ( − θ ) {\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin(-\theta )} cos ( − θ ) = + cos θ {\displaystyle \cos(-\theta )=+\cos \theta } cos ( π 2 − θ ) = sin θ {\displaystyle \cos \left({\tfrac {\pi }{2}}-\theta \right)=\sin \theta } cos ( π − θ ) = − cos θ {\displaystyle \cos(\pi -\theta )=-\cos \theta } cos ( 3 π 2 − θ ) = − sin θ {\displaystyle \cos \left({\tfrac {3\pi }{2}}-\theta \right)=-\sin \theta } cos ( 2 π − θ ) = + cos ( θ ) = cos ( − θ ) {\displaystyle \cos(2\pi -\theta )=+\cos(\theta )=\cos(-\theta )} tan ( − θ ) = − tan θ {\displaystyle \tan(-\theta )=-\tan \theta } tan ( π 2 − θ ) = cot θ {\displaystyle \tan \left({\tfrac {\pi }{2}}-\theta \right)=\cot \theta } tan ( π − θ ) = − tan θ {\displaystyle \tan(\pi -\theta )=-\tan \theta } tan ( 3 π 2 − θ ) = + cot θ {\displaystyle \tan \left({\tfrac {3\pi }{2}}-\theta \right)=+\cot \theta } tan ( 2 π − θ ) = − tan ( θ ) = tan ( − θ ) {\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan(-\theta )} csc ( − θ ) = − csc θ {\displaystyle \csc(-\theta )=-\csc \theta } csc ( π 2 − θ ) = sec θ {\displaystyle \csc \left({\tfrac {\pi }{2}}-\theta \right)=\sec \theta } csc ( π − θ ) = + csc θ {\displaystyle \csc(\pi -\theta )=+\csc \theta } csc ( 3 π 2 − θ ) = − sec θ {\displaystyle \csc \left({\tfrac {3\pi }{2}}-\theta \right)=-\sec \theta } csc ( 2 π − θ ) = − csc ( θ ) = csc ( − θ ) {\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc(-\theta )} sec ( − θ ) = + sec θ {\displaystyle \sec(-\theta )=+\sec \theta } sec ( π 2 − θ ) = csc θ {\displaystyle \sec \left({\tfrac {\pi }{2}}-\theta \right)=\csc \theta } sec ( π − θ ) = − sec θ {\displaystyle \sec(\pi -\theta )=-\sec \theta } sec ( 3 π 2 − θ ) = − csc θ {\displaystyle \sec \left({\tfrac {3\pi }{2}}-\theta \right)=-\csc \theta } sec ( 2 π − θ ) = + sec ( θ ) = sec ( − θ ) {\displaystyle \sec(2\pi -\theta )=+\sec(\theta )=\sec(-\theta )} cot ( − θ ) = − cot θ {\displaystyle \cot(-\theta )=-\cot \theta } cot ( π 2 − θ ) = tan θ {\displaystyle \cot \left({\tfrac {\pi }{2}}-\theta \right)=\tan \theta } cot ( π − θ ) = − cot θ {\displaystyle \cot(\pi -\theta )=-\cot \theta } cot ( 3 π 2 − θ ) = + tan θ {\displaystyle \cot \left({\tfrac {3\pi }{2}}-\theta \right)=+\tan \theta } cot ( 2 π − θ ) = − cot ( θ ) = cot ( − θ ) {\displaystyle \cot(2\pi -\theta )=-\cot(\theta )=\cot(-\theta )}
Преобразование координат ( a , b ) при сдвиге угла θ {\displaystyle \theta } π 2 {\displaystyle {\frac {\pi }{2}}} Сдвиг на четверть периода Сдвиг на полпериода Сдвиг на полные периоды [4] Период sin ( θ ± π 2 ) = ± cos θ {\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta } sin ( θ + π ) = − sin θ {\displaystyle \sin(\theta +\pi )=-\sin \theta } sin ( θ + k ⋅ 2 π ) = + sin θ {\displaystyle \sin(\theta +k\cdot 2\pi )=+\sin \theta } 2 π {\displaystyle 2\pi } cos ( θ ± π 2 ) = ∓ sin θ {\displaystyle \cos(\theta \pm {\tfrac {\pi }{2}})=\mp \sin \theta } cos ( θ + π ) = − cos θ {\displaystyle \cos(\theta +\pi )=-\cos \theta } cos ( θ + k ⋅ 2 π ) = + cos θ {\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta } 2 π {\displaystyle 2\pi } csc ( θ ± π 2 ) = ± sec θ {\displaystyle \csc(\theta \pm {\tfrac {\pi }{2}})=\pm \sec \theta } csc ( θ + π ) = − csc θ {\displaystyle \csc(\theta +\pi )=-\csc \theta } csc ( θ + k ⋅ 2 π ) = + csc θ {\displaystyle \csc(\theta +k\cdot 2\pi )=+\csc \theta } 2 π {\displaystyle 2\pi } sec ( θ ± π 2 ) = ∓ csc θ {\displaystyle \sec(\theta \pm {\tfrac {\pi }{2}})=\mp \csc \theta } sec ( θ + π ) = − sec θ {\displaystyle \sec(\theta +\pi )=-\sec \theta } sec ( θ + k ⋅ 2 π ) = + sec θ {\displaystyle \sec(\theta +k\cdot 2\pi )=+\sec \theta } 2 π {\displaystyle 2\pi } tan ( θ ± π 4 ) = tan θ ± 1 1 ∓ tan θ {\displaystyle \tan(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\tan \theta \pm 1}{1\mp \tan \theta }}} tan ( θ + π 2 ) = − cot θ {\displaystyle \tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta } tan ( θ + k ⋅ π ) = + tan θ {\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta } π {\displaystyle \pi } cot ( θ ± π 4 ) = cot θ ∓ 1 1 ± cot θ {\displaystyle \cot(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\cot \theta \mp 1}{1\pm \cot \theta }}} cot ( θ + π 2 ) = − tan θ {\displaystyle \cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta } cot ( θ + k ⋅ π ) = + cot θ {\displaystyle \cot(\theta +k\cdot \pi )=+\cot \theta } π {\displaystyle \pi }
Знак тригонометрических функций зависит от квадранта угла. Если − π < θ ≤ π {\displaystyle {-\pi }<\theta \leq \pi } Sign — знаковая функция ,
sgn ( sin θ ) = sgn ( csc θ ) = { + 1 if 0 < θ < π − 1 if − π < θ < 0 0 if θ ∈ { 0 , π } sgn ( cos θ ) = sgn ( sec θ ) = { + 1 if − 1 2 π < θ < 1 2 π − 1 if − π < θ < − 1 2 π or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 1 2 π } sgn ( tan θ ) = sgn ( cot θ ) = { + 1 if − π < θ < − 1 2 π or 0 < θ < 1 2 π − 1 if − 1 2 π < θ < 0 or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 0 , 1 2 π , π } {\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}
Тригонометрические функции периодические с общим периодом. 2 π , {\displaystyle 2\pi ,} θ вне интервала ( − π , π ] , {\displaystyle ({-\pi },\pi ],} § Сдвиги и периодичность выше).
Иллюстрация формул сложения синуса и косинуса острых углов. Выделенный отрезок имеет единичную длину. Диаграмма, показывающая тождества угловой разности для sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} Они также известны как теоремы сложения и вычитания углов (или формулы ). sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β {\displaystyle {\begin{aligned}\sin(\alpha +\beta )&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\\sin(\alpha -\beta )&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\\cos(\alpha +\beta )&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\cos(\alpha -\beta )&=\cos \alpha \cos \beta +\sin \alpha \sin \beta \end{aligned}}}
Тождества угловой разности для sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} − β {\displaystyle -\beta } β {\displaystyle \beta } sin ( − β ) = − sin ( β ) {\displaystyle \sin(-\beta )=-\sin(\beta )} cos ( − β ) = cos ( β ) {\displaystyle \cos(-\beta )=\cos(\beta )}
Эти тождества суммированы в первых двух строках следующей таблицы, которая также включает тождества суммы и разности для других тригонометрических функций.
Его sin ( α ± β ) {\displaystyle \sin(\alpha \pm \beta )} = {\displaystyle =} sin α cos β ± cos α sin β {\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta } [5] [6] Косинус cos ( α ± β ) {\displaystyle \cos(\alpha \pm \beta )} = {\displaystyle =} cos α cos β ∓ sin α sin β {\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta } [6] [7] Касательная tan ( α ± β ) {\displaystyle \tan(\alpha \pm \beta )} = {\displaystyle =} tan α ± tan β 1 ∓ tan α tan β {\displaystyle {\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}} [6] [8] Косеканс csc ( α ± β ) {\displaystyle \csc(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β sec α csc β ± csc α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta }}} [9] секанс sec ( α ± β ) {\displaystyle \sec(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β csc α csc β ∓ sec α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta }}} [9] Котангенс cot ( α ± β ) {\displaystyle \cot(\alpha \pm \beta )} = {\displaystyle =} cot α cot β ∓ 1 cot β ± cot α {\displaystyle {\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}} [6] [10] Арксинус arcsin x ± arcsin y {\displaystyle \arcsin x\pm \arcsin y} = {\displaystyle =} arcsin ( x 1 − y 2 ± y 1 − x 2 ) {\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}}}\right)} [11] Арккосинус arccos x ± arccos y {\displaystyle \arccos x\pm \arccos y} = {\displaystyle =} arccos ( x y ∓ ( 1 − x 2 ) ( 1 − y 2 ) ) {\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)} [12] Арктангенс arctan x ± arctan y {\displaystyle \arctan x\pm \arctan y} = {\displaystyle =} arctan ( x ± y 1 ∓ x y ) {\displaystyle \arctan \left({\frac {x\pm y}{1\mp xy}}\right)} [13] Арккотангенс arccot x ± arccot y {\displaystyle \operatorname {arccot} x\pm \operatorname {arccot} y} = {\displaystyle =} arccot ( x y ∓ 1 y ± x ) {\displaystyle \operatorname {arccot} \left({\frac {xy\mp 1}{y\pm x}}\right)}
Синусы и косинусы сумм бесконечного числа углов [ редактировать ] Когда сериал ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}} сходится абсолютно тогда
sin ( ∑ i = 1 ∞ θ i ) = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) cos ( ∑ i = 1 ∞ θ i ) = ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) . {\displaystyle {\begin{aligned}{\sin }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggl )}&=\sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\!\!\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}\\{\cos }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggr )}&=\sum _{{\text{even}}\ k\geq 0}(-1)^{\frac {k}{2}}\,\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}.\end{aligned}}}
Потому что сериал ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}} lim i → ∞ θ i = 0 , {\textstyle \lim _{i\to \infty }\theta _{i}=0,} lim i → ∞ sin θ i = 0 , {\textstyle \lim _{i\to \infty }\sin \theta _{i}=0,} lim i → ∞ cos θ i = 1. {\textstyle \lim _{i\to \infty }\cos \theta _{i}=1.} косинусоидальных множителей. Члены с бесконечным числом синусоидальных множителей обязательно будут равны нулю.
Когда только конечное число углов θ i {\displaystyle \theta _{i}}
Позволять e k {\displaystyle e_{k}} k = 0 , 1 , 2 , 3 , … {\displaystyle k=0,1,2,3,\ldots } k- й степени элементарный симметричный полином от переменных x i = tan θ i {\displaystyle x_{i}=\tan \theta _{i}} i = 0 , 1 , 2 , 3 , … , {\displaystyle i=0,1,2,3,\ldots ,}
e 0 = 1 e 1 = ∑ i x i = ∑ i tan θ i e 2 = ∑ i < j x i x j = ∑ i < j tan θ i tan θ j e 3 = ∑ i < j < k x i x j x k = ∑ i < j < k tan θ i tan θ j tan θ k ⋮ ⋮ {\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}
Затем
tan ( ∑ i θ i ) = sin ( ∑ i θ i ) / ∏ i cos θ i cos ( ∑ i θ i ) / ∏ i cos θ i = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i = e 1 − e 3 + e 5 − ⋯ e 0 − e 2 + e 4 − ⋯ cot ( ∑ i θ i ) = e 0 − e 2 + e 4 − ⋯ e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
используя приведенные выше формулы суммы синуса и косинуса.
Количество слагаемых в правой части зависит от количества слагаемых в левой части.
Например: tan ( θ 1 + θ 2 ) = e 1 e 0 − e 2 = x 1 + x 2 1 − x 1 x 2 = tan θ 1 + tan θ 2 1 − tan θ 1 tan θ 2 , tan ( θ 1 + θ 2 + θ 3 ) = e 1 − e 3 e 0 − e 2 = ( x 1 + x 2 + x 3 ) − ( x 1 x 2 x 3 ) 1 − ( x 1 x 2 + x 1 x 3 + x 2 x 3 ) , tan ( θ 1 + θ 2 + θ 3 + θ 4 ) = e 1 − e 3 e 0 − e 2 + e 4 = ( x 1 + x 2 + x 3 + x 4 ) − ( x 1 x 2 x 3 + x 1 x 2 x 4 + x 1 x 3 x 4 + x 2 x 3 x 4 ) 1 − ( x 1 x 2 + x 1 x 3 + x 1 x 4 + x 2 x 3 + x 2 x 4 + x 3 x 4 ) + ( x 1 x 2 x 3 x 4 ) , {\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
и так далее. Случай лишь конечного числа членов может быть доказан с помощью математической индукции . [14] [15]
sec ( ∑ i θ i ) = ∏ i sec θ i e 0 − e 2 + e 4 − ⋯ csc ( ∑ i θ i ) = ∏ i sec θ i e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
где e k {\displaystyle e_{k}} k-й степени элементарный симметричный полином от n переменных x i = tan θ i , {\displaystyle x_{i}=\tan \theta _{i},} i = 1 , … , n , {\displaystyle i=1,\ldots ,n,} [16]
Например,
sec ( α + β + γ ) = sec α sec β sec γ 1 − tan α tan β − tan α tan γ − tan β tan γ csc ( α + β + γ ) = sec α sec β sec γ tan α + tan β + tan γ − tan α tan β tan γ . {\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}
Диаграмма, иллюстрирующая связь между теоремой Птолемея и тригонометрическим тождеством суммы углов для синуса. Теорема Птолемея утверждает, что сумма произведений длин противоположных сторон равна произведению длин диагоналей. Когда эти длины сторон выражаются через значения sin и cos, показанные на рисунке выше, это дает тригонометрическое тождество суммы углов для синуса: sin( α + β ) = sin α cos β + cos α sin β . Теорема Птолемея важна в истории тригонометрических тождеств, поскольку именно ею были впервые доказаны результаты, эквивалентные формулам суммы и разности для синуса и косинуса. Он утверждает, что в вписанном четырехугольнике A B C D {\displaystyle ABCD} [17]
По Фалеса теореме ∠ D A B {\displaystyle \angle DAB} ∠ D C B {\displaystyle \angle DCB} D A B {\displaystyle DAB} D C B {\displaystyle DCB} B D ¯ {\displaystyle {\overline {BD}}} A B ¯ = sin α {\displaystyle {\overline {AB}}=\sin \alpha } A D ¯ = cos α {\displaystyle {\overline {AD}}=\cos \alpha } B C ¯ = sin β {\displaystyle {\overline {BC}}=\sin \beta } C D ¯ = cos β {\displaystyle {\overline {CD}}=\cos \beta }
По теореме о вписанном угле центральный угол, опирающийся на хорду A C ¯ {\displaystyle {\overline {AC}}} ∠ A D C {\displaystyle \angle ADC} 2 ( α + β ) {\displaystyle 2(\alpha +\beta )} α + β {\displaystyle \alpha +\beta } 1 2 {\textstyle {\frac {1}{2}}} A C ¯ {\displaystyle {\overline {AC}}} 2 × 1 2 sin ( α + β ) {\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )}
Когда эти значения подставляются в утверждение теоремы Птолемея о том, что | A C ¯ | ⋅ | B D ¯ | = | A B ¯ | ⋅ | C D ¯ | + | A D ¯ | ⋅ | B C ¯ | {\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {AD}}|\cdot |{\overline {BC}}|} sin ( α + β ) = sin α cos β + cos α sin β {\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta } sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} C D ¯ {\displaystyle {\overline {CD}}} B D ¯ {\displaystyle {\overline {BD}}} [17]
Наглядная демонстрация формулы двойного угла для синуса. Для приведенного выше равнобедренного треугольника с единичными сторонами и углом 2 θ {\displaystyle 2\theta } 1/2 основание × × высота рассчитывается в двух ориентациях. В вертикальном положении площадь sin θ cos θ {\displaystyle \sin \theta \cos \theta } 1 2 sin 2 θ {\textstyle {\frac {1}{2}}\sin 2\theta } sin 2 θ = 2 sin θ cos θ . {\displaystyle \sin 2\theta =2\sin \theta \cos \theta .} Формулы удвоения угла. [20]
sin ( 2 θ ) = 2 sin θ cos θ = ( sin θ + cos θ ) 2 − 1 = 2 tan θ 1 + tan 2 θ {\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }}} cos ( 2 θ ) = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ = 1 − tan 2 θ 1 + tan 2 θ {\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}} tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ = 1 − tan 2 θ 2 tan θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {1-\tan ^{2}\theta }{2\tan \theta }}} sec ( 2 θ ) = sec 2 θ 2 − sec 2 θ = 1 + tan 2 θ 1 − tan 2 θ {\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }}} csc ( 2 θ ) = sec θ csc θ 2 = 1 + tan 2 θ 2 tan θ {\displaystyle \csc(2\theta )={\frac {\sec \theta \csc \theta }{2}}={\frac {1+\tan ^{2}\theta }{2\tan \theta }}} Формулы тройных углов. [20]
sin ( 3 θ ) = 3 sin θ − 4 sin 3 θ = 4 sin θ sin ( π 3 − θ ) sin ( π 3 + θ ) {\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)} cos ( 3 θ ) = 4 cos 3 θ − 3 cos θ = 4 cos θ cos ( π 3 − θ ) cos ( π 3 + θ ) {\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)} tan ( 3 θ ) = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ = tan θ tan ( π 3 − θ ) tan ( π 3 + θ ) {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)} cot ( 3 θ ) = 3 cot θ − cot 3 θ 1 − 3 cot 2 θ {\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}} sec ( 3 θ ) = sec 3 θ 4 − 3 sec 2 θ {\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}} csc ( 3 θ ) = csc 3 θ 3 csc 2 θ − 4 {\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}} Формулы для нескольких углов. [21]
sin ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) cos n − k θ sin k θ = sin θ ∑ i = 0 ( n + 1 ) / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i + 1 ) ( i j ) cos n − 2 ( i − j ) − 1 θ = 2 ( n − 1 ) ∏ k = 0 n − 1 sin ( k π / n + θ ) {\displaystyle {\begin{aligned}\sin(n\theta )&=\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i+1}{i \choose j}\cos ^{n-2(i-j)-1}\theta \\{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}}} cos ( n θ ) = ∑ k even ( − 1 ) k 2 ( n k ) cos n − k θ sin k θ = ∑ i = 0 n / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i ) ( i j ) cos n − 2 ( i − j ) θ {\displaystyle \cos(n\theta )=\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sum _{i=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta } cos ( ( 2 n + 1 ) θ ) = ( − 1 ) n 2 2 n ∏ k = 0 2 n cos ( k π / ( 2 n + 1 ) − θ ) {\displaystyle \cos((2n+1)\theta )=(-1)^{n}2^{2n}\prod _{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )} cos ( 2 n θ ) = ( − 1 ) n 2 2 n − 1 ∏ k = 0 2 n − 1 cos ( ( 1 + 2 k ) π / ( 4 n ) − θ ) {\displaystyle \cos(2n\theta )=(-1)^{n}2^{2n-1}\prod _{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )} tan ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) tan k θ ∑ k even ( − 1 ) k 2 ( n k ) tan k θ {\displaystyle \tan(n\theta )={\frac {\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\tan ^{k}\theta }}} Метод Чебышева представляет собой рекурсивный алгоритм нахождения n-й формулы кратного угла, зная ( n − 1 ) {\displaystyle (n-1)} ( n − 2 ) {\displaystyle (n-2)} [22]
cos ( n x ) {\displaystyle \cos(nx)} cos ( ( n − 1 ) x ) {\displaystyle \cos((n-1)x)} cos ( ( n − 2 ) x ) {\displaystyle \cos((n-2)x)} cos ( x ) {\displaystyle \cos(x)}
cos ( n x ) = 2 cos x cos ( ( n − 1 ) x ) − cos ( ( n − 2 ) x ) . {\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-2)x).}
Это можно доказать, сложив формулы
cos ( ( n − 1 ) x + x ) = cos ( ( n − 1 ) x ) cos x − sin ( ( n − 1 ) x ) sin x cos ( ( n − 1 ) x − x ) = cos ( ( n − 1 ) x ) cos x + sin ( ( n − 1 ) x ) sin x {\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos((n-1)x)\cos x-\sin((n-1)x)\sin x\\\cos((n-1)x-x)&=\cos((n-1)x)\cos x+\sin((n-1)x)\sin x\end{aligned}}}
По индукции следует, что cos ( n x ) {\displaystyle \cos(nx)} cos x , {\displaystyle \cos x,} Полиномы Чебышева#Тригонометрическое определение .
Сходным образом, sin ( n x ) {\displaystyle \sin(nx)} sin ( ( n − 1 ) x ) , {\displaystyle \sin((n-1)x),} sin ( ( n − 2 ) x ) , {\displaystyle \sin((n-2)x),} cos x {\displaystyle \cos x} sin ( n x ) = 2 cos x sin ( ( n − 1 ) x ) − sin ( ( n − 2 ) x ) {\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-2)x)} sin ( ( n − 1 ) x + x ) {\displaystyle \sin((n-1)x+x)} sin ( ( n − 1 ) x − x ) . {\displaystyle \sin((n-1)x-x).}
Для целей, аналогичных цели метода Чебышева, для касательной можно записать:
tan ( n x ) = tan ( ( n − 1 ) x ) + tan x 1 − tan ( ( n − 1 ) x ) tan x . {\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}}\,.}
sin θ 2 = sgn ( sin θ 2 ) 1 − cos θ 2 cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 tan θ 2 = 1 − cos θ sin θ = sin θ 1 + cos θ = csc θ − cot θ = tan θ 1 + sec θ = sgn ( sin θ ) 1 − cos θ 1 + cos θ = − 1 + sgn ( cos θ ) 1 + tan 2 θ tan θ cot θ 2 = 1 + cos θ sin θ = sin θ 1 − cos θ = csc θ + cot θ = sgn ( sin θ ) 1 + cos θ 1 − cos θ sec θ 2 = sgn ( cos θ 2 ) 2 1 + cos θ csc θ 2 = sgn ( sin θ 2 ) 2 1 − cos θ {\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}} [23] [24]
Также tan η ± θ 2 = sin η ± sin θ cos η + cos θ tan ( θ 2 + π 4 ) = sec θ + tan θ 1 − sin θ 1 + sin θ = | 1 − tan θ 2 | | 1 + tan θ 2 | {\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{aligned}}}
Их можно показать, используя либо тождества суммы и разности, либо формулы нескольких углов.
Его Косинус Касательная Котангенс Формула двойного угла [25] [26] sin ( 2 θ ) = 2 sin θ cos θ = 2 tan θ 1 + tan 2 θ {\displaystyle {\begin{aligned}\sin(2\theta )&=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}} cos ( 2 θ ) = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ = 1 − tan 2 θ 1 + tan 2 θ {\displaystyle {\begin{aligned}\cos(2\theta )&=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}} tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}} Формула тройного угла [18] [27] sin ( 3 θ ) = − sin 3 θ + 3 cos 2 θ sin θ = − 4 sin 3 θ + 3 sin θ {\displaystyle {\begin{aligned}\sin(3\theta )&=-\sin ^{3}\theta +3\cos ^{2}\theta \sin \theta \\&=-4\sin ^{3}\theta +3\sin \theta \end{aligned}}} cos ( 3 θ ) = cos 3 θ − 3 sin 2 θ cos θ = 4 cos 3 θ − 3 cos θ {\displaystyle {\begin{aligned}\cos(3\theta )&=\cos ^{3}\theta -3\sin ^{2}\theta \cos \theta \\&=4\cos ^{3}\theta -3\cos \theta \end{aligned}}} tan ( 3 θ ) = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}} cot ( 3 θ ) = 3 cot θ − cot 3 θ 1 − 3 cot 2 θ {\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}} Формула половинного угла [23] [24] sin θ 2 = sgn ( sin θ 2 ) 1 − cos θ 2 ( or sin 2 θ 2 = 1 − cos θ 2 ) {\displaystyle {\begin{aligned}&\sin {\frac {\theta }{2}}=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\\\&\left({\text{or }}\sin ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{2}}\right)\end{aligned}}} cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 ( or cos 2 θ 2 = 1 + cos θ 2 ) {\displaystyle {\begin{aligned}&\cos {\frac {\theta }{2}}=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\\\&\left({\text{or }}\cos ^{2}{\frac {\theta }{2}}={\frac {1+\cos \theta }{2}}\right)\end{aligned}}} tan θ 2 = csc θ − cot θ = ± 1 − cos θ 1 + cos θ = sin θ 1 + cos θ = 1 − cos θ sin θ tan η + θ 2 = sin η + sin θ cos η + cos θ tan ( θ 2 + π 4 ) = sec θ + tan θ 1 − sin θ 1 + sin θ = | 1 − tan θ 2 | | 1 + tan θ 2 | tan θ 2 = tan θ 1 + 1 + tan 2 θ for θ ∈ ( − π 2 , π 2 ) {\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\[5pt]\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}} cot θ 2 = csc θ + cot θ = ± 1 + cos θ 1 − cos θ = sin θ 1 − cos θ = 1 + cos θ sin θ {\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}
Тот факт, что формула тройного угла для синуса и косинуса включает в себя степени только одной функции, позволяет связать геометрическую задачу построения циркуля и линейки с трисекции угла алгебраической задачей решения кубического уравнения , что позволяет доказать что трисекция вообще невозможна с использованием данных инструментов теории поля . [ нужна ссылка
Формула вычисления тригонометрических тождеств для угла в одну треть существует, но она требует нахождения нулей кубического уравнения 4 x 3 − 3 x + d = 0 , где x {\displaystyle x} d — известное значение косинуса под полным углом. Однако дискриминант этого уравнения положителен, поэтому это уравнение имеет три вещественных корня (из которых только один является решением косинуса трети угла). Ни одно из этих решений не сводится к реальному алгебраическому выражению , поскольку они используют промежуточные комплексные числа под кубическими корнями .
Получено решением второго и третьего вариантов формулы косинуса двойного угла.
Его Косинус Другой sin 2 θ = 1 − cos ( 2 θ ) 2 {\displaystyle \sin ^{2}\theta ={\frac {1-\cos(2\theta )}{2}}} cos 2 θ = 1 + cos ( 2 θ ) 2 {\displaystyle \cos ^{2}\theta ={\frac {1+\cos(2\theta )}{2}}} sin 2 θ cos 2 θ = 1 − cos ( 4 θ ) 8 {\displaystyle \sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos(4\theta )}{8}}} sin 3 θ = 3 sin θ − sin ( 3 θ ) 4 {\displaystyle \sin ^{3}\theta ={\frac {3\sin \theta -\sin(3\theta )}{4}}} cos 3 θ = 3 cos θ + cos ( 3 θ ) 4 {\displaystyle \cos ^{3}\theta ={\frac {3\cos \theta +\cos(3\theta )}{4}}} sin 3 θ cos 3 θ = 3 sin ( 2 θ ) − sin ( 6 θ ) 32 {\displaystyle \sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin(2\theta )-\sin(6\theta )}{32}}} sin 4 θ = 3 − 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \sin ^{4}\theta ={\frac {3-4\cos(2\theta )+\cos(4\theta )}{8}}} cos 4 θ = 3 + 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \cos ^{4}\theta ={\frac {3+4\cos(2\theta )+\cos(4\theta )}{8}}} sin 4 θ cos 4 θ = 3 − 4 cos ( 4 θ ) + cos ( 8 θ ) 128 {\displaystyle \sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos(4\theta )+\cos(8\theta )}{128}}} sin 5 θ = 10 sin θ − 5 sin ( 3 θ ) + sin ( 5 θ ) 16 {\displaystyle \sin ^{5}\theta ={\frac {10\sin \theta -5\sin(3\theta )+\sin(5\theta )}{16}}} cos 5 θ = 10 cos θ + 5 cos ( 3 θ ) + cos ( 5 θ ) 16 {\displaystyle \cos ^{5}\theta ={\frac {10\cos \theta +5\cos(3\theta )+\cos(5\theta )}{16}}} sin 5 θ cos 5 θ = 10 sin ( 2 θ ) − 5 sin ( 6 θ ) + sin ( 10 θ ) 512 {\displaystyle \sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin(2\theta )-5\sin(6\theta )+\sin(10\theta )}{512}}}
Формула косинусного приведения в степень: наглядная диаграмма. Красный, оранжевый и синий треугольники подобны, а красный и оранжевый треугольники конгруэнтны. Гипотенуза A D ¯ {\displaystyle {\overline {AD}}} 2 cos θ {\displaystyle 2\cos \theta } ∠ D A E {\displaystyle \angle DAE} θ {\displaystyle \theta } A E ¯ {\displaystyle {\overline {AE}}} 2 cos 2 θ {\displaystyle 2\cos ^{2}\theta } B D ¯ {\displaystyle {\overline {BD}}} A F ¯ {\displaystyle {\overline {AF}}} 1 + cos ( 2 θ ) {\displaystyle 1+\cos(2\theta )} 2 cos 2 θ = 1 + cos ( 2 θ ) {\displaystyle 2\cos ^{2}\theta =1+\cos(2\theta )} 2 {\displaystyle 2} cos 2 θ = {\displaystyle \cos ^{2}\theta =} 1 2 ( 1 + cos ( 2 θ ) ) {\textstyle {\frac {1}{2}}(1+\cos(2\theta ))} θ {\displaystyle \theta } θ / 2 {\displaystyle \theta /2} cos ( θ / 2 ) = ± ( 1 + cos θ ) / 2 . {\textstyle \cos \left(\theta /2\right)=\pm {\sqrt {\left(1+\cos \theta \right)/2}}.} Формула снижения синусоидальной мощности: наглядная диаграмма. Заштрихованные синий и зеленый треугольники и треугольник, обведенный красным. E B D {\displaystyle EBD} θ {\displaystyle \theta } B D ¯ {\displaystyle {\overline {BD}}} 2 sin θ {\displaystyle 2\sin \theta } D E ¯ {\displaystyle {\overline {DE}}} 2 sin 2 θ {\displaystyle 2\sin ^{2}\theta } A E ¯ {\displaystyle {\overline {AE}}} cos 2 θ {\displaystyle \cos 2\theta } A E ¯ {\displaystyle {\overline {AE}}} D E ¯ {\displaystyle {\overline {DE}}} A D ¯ {\displaystyle {\overline {AD}}} cos 2 θ + 2 sin 2 θ = 1 {\displaystyle \cos 2\theta +2\sin ^{2}\theta =1} cos 2 θ {\displaystyle \cos 2\theta } sin 2 θ = {\displaystyle \sin ^{2}\theta =} 1 2 ( 1 − cos ( 2 θ ) ) {\textstyle {\frac {1}{2}}(1-\cos(2\theta ))} θ {\displaystyle \theta } θ / 2 {\displaystyle \theta /2} sin ( θ / 2 ) = ± ( 1 − cos θ ) / 2 . {\textstyle \sin \left(\theta /2\right)=\pm {\sqrt {\left(1-\cos \theta \right)/2}}.} E B ¯ {\displaystyle {\overline {EB}}} sin 2 θ = 2 sin θ cos θ {\displaystyle \sin 2\theta =2\sin \theta \cos \theta }
В общих чертах полномочия sin θ {\displaystyle \sin \theta } cos θ {\displaystyle \cos \theta } формулы Де Муавра , формулы Эйлера и биномиальной теоремы .
если н ... cos n θ {\displaystyle \cos ^{n}\theta } sin n θ {\displaystyle \sin ^{n}\theta } n нечетное cos n θ = 2 2 n ∑ k = 0 n − 1 2 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}} sin n θ = 2 2 n ∑ k = 0 n − 1 2 ( − 1 ) ( n − 1 2 − k ) ( n k ) sin ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {{\big (}(n-2k)\theta {\big )}}} n четное cos n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}} sin n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( − 1 ) ( n 2 − k ) ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}
Тождества произведения к сумме и суммы к произведению [ редактировать ] Доказательство косинусного тождества суммы и разности для расчета простафереза с использованием равнобедренного треугольника. Тождества произведения к сумме [28] формулы простафереза можно доказать, разложив их правые части с помощью теорем сложения углов . Исторически первые четыре из них были известны как формулы Вернера , в честь Иоганна Вернера , который использовал их для астрономических расчетов. [29] амплитудную модуляцию для применения формул преобразования суммы в сумму, а также детектор биений (акустика) и фазовый детектор для применения формул преобразования суммы в произведение.
cos θ cos φ = cos ( θ − φ ) + cos ( θ + φ ) 2 {\displaystyle \cos \theta \,\cos \varphi ={\cos(\theta -\varphi )+\cos(\theta +\varphi ) \over 2}} sin θ sin φ = cos ( θ − φ ) − cos ( θ + φ ) 2 {\displaystyle \sin \theta \,\sin \varphi ={\cos(\theta -\varphi )-\cos(\theta +\varphi ) \over 2}} sin θ cos φ = sin ( θ + φ ) + sin ( θ − φ ) 2 {\displaystyle \sin \theta \,\cos \varphi ={\sin(\theta +\varphi )+\sin(\theta -\varphi ) \over 2}} cos θ sin φ = sin ( θ + φ ) − sin ( θ − φ ) 2 {\displaystyle \cos \theta \,\sin \varphi ={\sin(\theta +\varphi )-\sin(\theta -\varphi ) \over 2}} tan θ tan φ = cos ( θ − φ ) − cos ( θ + φ ) cos ( θ − φ ) + cos ( θ + φ ) {\displaystyle \tan \theta \,\tan \varphi ={\frac {\cos(\theta -\varphi )-\cos(\theta +\varphi )}{\cos(\theta -\varphi )+\cos(\theta +\varphi )}}} tan θ cot φ = sin ( θ + φ ) + sin ( θ − φ ) sin ( θ + φ ) − sin ( θ − φ ) {\displaystyle \tan \theta \,\cot \varphi ={\frac {\sin(\theta +\varphi )+\sin(\theta -\varphi )}{\sin(\theta +\varphi )-\sin(\theta -\varphi )}}} ∏ k = 1 n cos θ k = 1 2 n ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) where e = ( e 1 , … , e n ) ∈ S = { 1 , − 1 } n {\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[6pt]&{\text{where }}e=(e_{1},\ldots ,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}} ∏ k = 1 n sin θ k = ( − 1 ) ⌊ n 2 ⌋ 2 n { ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j if n is even , ∑ e ∈ S sin ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j if n is odd {\displaystyle \prod _{k=1}^{n}\sin \theta _{k}={\frac {(-1)^{\left\lfloor {\frac {n}{2}}\right\rfloor }}{2^{n}}}{\begin{cases}\displaystyle \sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is even}},\\\displaystyle \sum _{e\in S}\sin(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is odd}}\end{cases}}} Диаграмма, иллюстрирующая тождества суммы и произведения для синуса и косинуса. Синий прямоугольный треугольник имеет угол θ {\displaystyle \theta } φ {\displaystyle \varphi } p {\displaystyle p} q {\displaystyle q} p = ( θ + φ ) / 2 {\displaystyle p=(\theta +\varphi )/2} q = ( θ − φ ) / 2 {\displaystyle q=(\theta -\varphi )/2} θ = p + q {\displaystyle \theta =p+q} φ = p − q {\displaystyle \varphi =p-q} A F G {\displaystyle AFG} F C E {\displaystyle FCE} cos q {\displaystyle \cos q} p {\displaystyle p} sin θ + sin φ {\displaystyle \sin \theta +\sin \varphi } 2 sin p cos q {\displaystyle 2\sin p\cos q} p {\displaystyle p} q {\displaystyle q} θ {\displaystyle \theta } φ {\displaystyle \varphi } sin θ + sin φ = 2 sin ( θ + φ 2 ) cos ( θ − φ 2 ) {\displaystyle \sin \theta +\sin \varphi =2\sin \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)} Тождества суммы к произведению следующие: [30]
sin θ ± sin φ = 2 sin ( θ ± φ 2 ) cos ( θ ∓ φ 2 ) {\displaystyle \sin \theta \pm \sin \varphi =2\sin \left({\frac {\theta \pm \varphi }{2}}\right)\cos \left({\frac {\theta \mp \varphi }{2}}\right)} cos θ + cos φ = 2 cos ( θ + φ 2 ) cos ( θ − φ 2 ) {\displaystyle \cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)} cos θ − cos φ = − 2 sin ( θ + φ 2 ) sin ( θ − φ 2 ) {\displaystyle \cos \theta -\cos \varphi =-2\sin \left({\frac {\theta +\varphi }{2}}\right)\sin \left({\frac {\theta -\varphi }{2}}\right)} tan θ ± tan φ = sin ( θ ± φ ) cos θ cos φ {\displaystyle \tan \theta \pm \tan \varphi ={\frac {\sin(\theta \pm \varphi )}{\cos \theta \,\cos \varphi }}} Чарльз Эрмит продемонстрировал следующее тождество. [31] a 1 , … , a n {\displaystyle a_{1},\ldots ,a_{n}} комплексными числами , никакие два из которых не отличаются на целое число, кратное π . Позволять
A n , k = ∏ 1 ≤ j ≤ n j ≠ k cot ( a k − a j ) {\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}
(в частности, A 1 , 1 , {\displaystyle A_{1,1},} пустым продуктом , это 1). Затем
cot ( z − a 1 ) ⋯ cot ( z − a n ) = cos n π 2 + ∑ k = 1 n A n , k cot ( z − a k ) . {\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi }{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k}).}
Простейшим нетривиальным примером является случай n = 2
cot ( z − a 1 ) cot ( z − a 2 ) = − 1 + cot ( a 1 − a 2 ) cot ( z − a 1 ) + cot ( a 2 − a 1 ) cot ( z − a 2 ) . {\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2}).}
Конечные произведения тригонометрических функций [ редактировать ] Для взаимно простых целых чисел n , m
∏ k = 1 n ( 2 a + 2 cos ( 2 π k m n + x ) ) = 2 ( T n ( a ) + ( − 1 ) n + m cos ( n x ) ) {\displaystyle \prod _{k=1}^{n}\left(2a+2\cos \left({\frac {2\pi km}{n}}+x\right)\right)=2\left(T_{n}(a)+{(-1)}^{n+m}\cos(nx)\right)}
где T n — полином Чебышева . [ нужна ссылка
Для функции синуса справедливо следующее соотношение
∏ k = 1 n − 1 sin ( k π n ) = n 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}.}
В более общем смысле для целого числа n > 0 [32]
sin ( n x ) = 2 n − 1 ∏ k = 0 n − 1 sin ( k n π + x ) = 2 n − 1 ∏ k = 1 n sin ( k n π − x ) . {\displaystyle \sin(nx)=2^{n-1}\prod _{k=0}^{n-1}\sin \left({\frac {k}{n}}\pi +x\right)=2^{n-1}\prod _{k=1}^{n}\sin \left({\frac {k}{n}}\pi -x\right).}
или записано в терминах аккорда функции crd x ≡ 2 sin 1 2 x {\textstyle \operatorname {crd} x\equiv 2\sin {\tfrac {1}{2}}x}
crd ( n x ) = ∏ k = 1 n crd ( k n 2 π − x ) . {\displaystyle \operatorname {crd} (nx)=\prod _{k=1}^{n}\operatorname {crd} \left({\frac {k}{n}}2\pi -x\right).}
Это происходит в результате факторизации многочлена z n − 1 {\textstyle z^{n}-1} корень из единицы ): для точки z на комплексной единичной окружности и целого числа n > 0
z n − 1 = ∏ k = 1 n z − exp ( k n 2 π i ) . {\displaystyle z^{n}-1=\prod _{k=1}^{n}z-\exp {\Bigl (}{\frac {k}{n}}2\pi i{\Bigr )}.}
Для некоторых целей важно знать, что любая линейная комбинация синусоидальных волн одного и того же периода или частоты, но с разными фазовыми сдвигами, также является синусоидальной волной с тем же периодом или частотой, но с другим фазовым сдвигом. Это полезно при синусоиды подборе данных , поскольку измеренные или наблюдаемые данные линейно связаны с a и b неизвестными базиса синфазных и квадратурных компонентов , приведенного ниже, что приводит к более простому якобиану по сравнению с таковым из c {\displaystyle c} φ {\displaystyle \varphi }
Линейная комбинация или гармоническое сложение синусоидальных и косинусоидальных волн эквивалентно одной синусоидальной волне со сдвигом фазы и масштабированной амплитудой. [33] [34]
a cos x + b sin x = c cos ( x + φ ) {\displaystyle a\cos x+b\sin x=c\cos(x+\varphi )}
где c {\displaystyle c} φ {\displaystyle \varphi }
c = sgn ( a ) a 2 + b 2 , φ = arctan ( − b / a ) , {\displaystyle {\begin{aligned}c&=\operatorname {sgn}(a){\sqrt {a^{2}+b^{2}}},\\\varphi &={\arctan }{\bigl (}{-b/a}{\bigr )},\end{aligned}}}
при условии a ≠ 0. {\displaystyle a\neq 0.}
В более общем смысле для произвольных фазовых сдвигов мы имеем
a sin ( x + θ a ) + b sin ( x + θ b ) = c sin ( x + φ ) {\displaystyle a\sin(x+\theta _{a})+b\sin(x+\theta _{b})=c\sin(x+\varphi )}
где c {\displaystyle c} φ {\displaystyle \varphi }
c 2 = a 2 + b 2 + 2 a b cos ( θ a − θ b ) , tan φ = a sin θ a + b sin θ b a cos θ a + b cos θ b . {\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}+2ab\cos \left(\theta _{a}-\theta _{b}\right),\\\tan \varphi &={\frac {a\sin \theta _{a}+b\sin \theta _{b}}{a\cos \theta _{a}+b\cos \theta _{b}}}.\end{aligned}}}
Общий случай гласит [34]
∑ i a i sin ( x + θ i ) = a sin ( x + θ ) , {\displaystyle \sum _{i}a_{i}\sin(x+\theta _{i})=a\sin(x+\theta ),} a 2 = ∑ i , j a i a j cos ( θ i − θ j ) {\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\theta _{i}-\theta _{j})} tan θ = ∑ i a i sin θ i ∑ i a i cos θ i . {\displaystyle \tan \theta ={\frac {\sum _{i}a_{i}\sin \theta _{i}}{\sum _{i}a_{i}\cos \theta _{i}}}.}
Эти личности, названные в честь Жозефа Луи Лагранжа : [35] [36] [37] ∑ k = 0 n sin k θ = cos 1 2 θ − cos ( ( n + 1 2 ) θ ) 2 sin 1 2 θ ∑ k = 0 n cos k θ = sin 1 2 θ + sin ( ( n + 1 2 ) θ ) 2 sin 1 2 θ {\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}} θ ≢ 0 ( mod 2 π ) . {\displaystyle \theta \not \equiv 0{\pmod {2\pi }}.}
Связанная функция — ядро Дирихле :
D n ( θ ) = 1 + 2 ∑ k = 1 n cos k θ = sin ( ( n + 1 2 ) θ ) sin 1 2 θ . {\displaystyle D_{n}(\theta )=1+2\sum _{k=1}^{n}\cos k\theta ={\frac {\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{\sin {\tfrac {1}{2}}\theta }}.}
Подобная идентичность [38]
∑ k = 1 n cos ( 2 k − 1 ) α = sin ( 2 n α ) 2 sin α . {\displaystyle \sum _{k=1}^{n}\cos(2k-1)\alpha ={\frac {\sin(2n\alpha )}{2\sin \alpha }}.}
Доказательство состоит в следующем. Используя тождества суммы углов и разностей , sin ( A + B ) − sin ( A − B ) = 2 cos A sin B . {\displaystyle \sin(A+B)-\sin(A-B)=2\cos A\sin B.}
2 sin α ∑ k = 1 n cos ( 2 k − 1 ) α = 2 sin α cos α + 2 sin α cos 3 α + 2 sin α cos 5 α + … + 2 sin α cos ( 2 n − 1 ) α {\displaystyle 2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha =2\sin \alpha \cos \alpha +2\sin \alpha \cos 3\alpha +2\sin \alpha \cos 5\alpha +\ldots +2\sin \alpha \cos(2n-1)\alpha }
2 sin α ∑ k = 1 n cos ( 2 k − 1 ) α = ∑ k = 1 n ( sin ( 2 k α ) − sin ( 2 ( k − 1 ) α ) ) = ( sin 2 α − sin 0 ) + ( sin 4 α − sin 2 α ) + ( sin 6 α − sin 4 α ) + … + ( sin ( 2 n α ) − sin ( 2 ( n − 1 ) α ) ) = sin ( 2 n α ) . {\displaystyle {\begin{aligned}&2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha \\&\quad =\sum _{k=1}^{n}(\sin(2k\alpha )-\sin(2(k-1)\alpha ))\\&\quad =(\sin 2\alpha -\sin 0)+(\sin 4\alpha -\sin 2\alpha )+(\sin 6\alpha -\sin 4\alpha )+\ldots +(\sin(2n\alpha )-\sin(2(n-1)\alpha ))\\&\quad =\sin(2n\alpha ).\end{aligned}}}
Итак, разделив эту формулу на 2 sin α {\displaystyle 2\sin \alpha }
Если f ( x ) {\displaystyle f(x)} дробно-линейным преобразованием f ( x ) = ( cos α ) x − sin α ( sin α ) x + cos α , {\displaystyle f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},} g ( x ) = ( cos β ) x − sin β ( sin β ) x + cos β , {\displaystyle g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},} f ( g ( x ) ) = g ( f ( x ) ) = ( cos ( α + β ) ) x − sin ( α + β ) ( sin ( α + β ) ) x + cos ( α + β ) . {\displaystyle f{\big (}g(x){\big )}=g{\big (}f(x){\big )}={\frac {{\big (}\cos(\alpha +\beta ){\big )}x-\sin(\alpha +\beta )}{{\big (}\sin(\alpha +\beta ){\big )}x+\cos(\alpha +\beta )}}.}
Если говорить более кратко, то если для всех α {\displaystyle \alpha } f α {\displaystyle f_{\alpha }} f {\displaystyle f} f α ∘ f β = f α + β . {\displaystyle f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.}
Если x {\displaystyle x} f ( x ) {\displaystyle f(x)} − α . {\displaystyle -\alpha .}
Формула Эйлера гласит, что для любого действительного числа x : [39] e i x = cos x + i sin x , {\displaystyle e^{ix}=\cos x+i\sin x,} я — мнимая единица . Замена − x на x дает нам: e − i x = cos ( − x ) + i sin ( − x ) = cos x − i sin x . {\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x.}
Эти два уравнения можно использовать для вычисления косинуса и синуса в терминах экспоненциальной функции . Конкретно, [40] [41] cos x = e i x + e − i x 2 {\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}} sin x = e i x − e − i x 2 i {\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}
Эти формулы полезны для доказательства многих других тригонометрических тождеств. Например, это е я ( θ + φ ) и я и iφ
cos( θ + φ ) + я sin( θ + φ ) = (cos θ + я sin θ ) (cos φ + я sin φ ) = (cos θ cos φ − sin θ sin φ ) + i (cos θ sin φ + грех θ потому что φ ) .
То, что действительная часть левой части равна действительной части правой части, является формулой сложения углов для косинуса. Равенство мнимых частей дает формулу сложения углов для синуса.
В следующей таблице тригонометрические функции и их обратные выражаются через экспоненциальную функцию и комплексный логарифм .
Функция Обратная функция [42] sin θ = e i θ − e − i θ 2 i {\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}} arcsin x = − i ln ( i x + 1 − x 2 ) {\displaystyle \arcsin x=-i\,\ln \left(ix+{\sqrt {1-x^{2}}}\right)} cos θ = e i θ + e − i θ 2 {\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}} arccos x = − i ln ( x + x 2 − 1 ) {\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)} tan θ = − i e i θ − e − i θ e i θ + e − i θ {\displaystyle \tan \theta =-i\,{\frac {e^{i\theta }-e^{-i\theta }}{e^{i\theta }+e^{-i\theta }}}} arctan x = i 2 ln ( i + x i − x ) {\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)} csc θ = 2 i e i θ − e − i θ {\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}} arccsc x = − i ln ( i x + 1 − 1 x 2 ) {\displaystyle \operatorname {arccsc} x=-i\,\ln \left({\frac {i}{x}}+{\sqrt {1-{\frac {1}{x^{2}}}}}\right)} sec θ = 2 e i θ + e − i θ {\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}} arcsec x = − i ln ( 1 x + i 1 − 1 x 2 ) {\displaystyle \operatorname {arcsec} x=-i\,\ln \left({\frac {1}{x}}+i{\sqrt {1-{\frac {1}{x^{2}}}}}\right)} cot θ = i e i θ + e − i θ e i θ − e − i θ {\displaystyle \cot \theta =i\,{\frac {e^{i\theta }+e^{-i\theta }}{e^{i\theta }-e^{-i\theta }}}} arccot x = i 2 ln ( x − i x + i ) {\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)} cis θ = e i θ {\displaystyle \operatorname {cis} \theta =e^{i\theta }} arccis x = − i ln x {\displaystyle \operatorname {arccis} x=-i\ln x}
При использовании разложения в степенной ряд для определения тригонометрических функций получаются следующие тождества: [43]
sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! , {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},} cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! . {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.} Для приложений к специальным функциям следующие формулы бесконечного произведения для тригонометрических функций: полезны [44] [45]
sin x = x ∏ n = 1 ∞ ( 1 − x 2 π 2 n 2 ) , cos x = ∏ n = 1 ∞ ( 1 − x 2 π 2 ( n − 1 2 ) ) 2 ) , sinh x = x ∏ n = 1 ∞ ( 1 + x 2 π 2 n 2 ) , cosh x = ∏ n = 1 ∞ ( 1 + x 2 π 2 ( n − 1 2 ) ) 2 ) . {\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\[10mu]\sinh x&=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right).\end{aligned}}}
Следующие тождества дают результат составления тригонометрической функции с обратной тригонометрической функцией. [46]
sin ( arcsin x ) = x cos ( arcsin x ) = 1 − x 2 tan ( arcsin x ) = x 1 − x 2 sin ( arccos x ) = 1 − x 2 cos ( arccos x ) = x tan ( arccos x ) = 1 − x 2 x sin ( arctan x ) = x 1 + x 2 cos ( arctan x ) = 1 1 + x 2 tan ( arctan x ) = x sin ( arccsc x ) = 1 x cos ( arccsc x ) = x 2 − 1 x tan ( arccsc x ) = 1 x 2 − 1 sin ( arcsec x ) = x 2 − 1 x cos ( arcsec x ) = 1 x tan ( arcsec x ) = x 2 − 1 sin ( arccot x ) = 1 1 + x 2 cos ( arccot x ) = x 1 + x 2 tan ( arccot x ) = 1 x {\displaystyle {\begin{aligned}\sin(\arcsin x)&=x&\cos(\arcsin x)&={\sqrt {1-x^{2}}}&\tan(\arcsin x)&={\frac {x}{\sqrt {1-x^{2}}}}\\\sin(\arccos x)&={\sqrt {1-x^{2}}}&\cos(\arccos x)&=x&\tan(\arccos x)&={\frac {\sqrt {1-x^{2}}}{x}}\\\sin(\arctan x)&={\frac {x}{\sqrt {1+x^{2}}}}&\cos(\arctan x)&={\frac {1}{\sqrt {1+x^{2}}}}&\tan(\arctan x)&=x\\\sin(\operatorname {arccsc} x)&={\frac {1}{x}}&\cos(\operatorname {arccsc} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\tan(\operatorname {arccsc} x)&={\frac {1}{\sqrt {x^{2}-1}}}\\\sin(\operatorname {arcsec} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\cos(\operatorname {arcsec} x)&={\frac {1}{x}}&\tan(\operatorname {arcsec} x)&={\sqrt {x^{2}-1}}\\\sin(\operatorname {arccot} x)&={\frac {1}{\sqrt {1+x^{2}}}}&\cos(\operatorname {arccot} x)&={\frac {x}{\sqrt {1+x^{2}}}}&\tan(\operatorname {arccot} x)&={\frac {1}{x}}\\\end{aligned}}}
Если мультипликативное обратное значение обеих частей каждого приведенного выше уравнения приводит к уравнениям для csc = 1 sin , sec = 1 cos , and cot = 1 tan . {\displaystyle \csc ={\frac {1}{\sin }},\;\sec ={\frac {1}{\cos }},{\text{ and }}\cot ={\frac {1}{\tan }}.} cot ( arcsin x ) {\displaystyle \cot(\arcsin x)} cot ( arcsin x ) = 1 tan ( arcsin x ) = 1 x 1 − x 2 = 1 − x 2 x {\displaystyle \cot(\arcsin x)={\frac {1}{\tan(\arcsin x)}}={\frac {1}{\frac {x}{\sqrt {1-x^{2}}}}}={\frac {\sqrt {1-x^{2}}}{x}}} csc ( arccos x ) {\displaystyle \csc(\arccos x)} sec ( arccos x ) {\displaystyle \sec(\arccos x)} csc ( arccos x ) = 1 sin ( arccos x ) = 1 1 − x 2 and sec ( arccos x ) = 1 cos ( arccos x ) = 1 x . {\displaystyle \csc(\arccos x)={\frac {1}{\sin(\arccos x)}}={\frac {1}{\sqrt {1-x^{2}}}}\qquad {\text{ and }}\quad \sec(\arccos x)={\frac {1}{\cos(\arccos x)}}={\frac {1}{x}}.}
Следующие тождества подразумеваются тождествами отражения . Они держатся всякий раз, когда x , r , s , − x , − r , and − s {\displaystyle x,r,s,-x,-r,{\text{ and }}-s} π 2 = arcsin ( x ) + arccos ( x ) = arctan ( r ) + arccot ( r ) = arcsec ( s ) + arccsc ( s ) π = arccos ( x ) + arccos ( − x ) = arccot ( r ) + arccot ( − r ) = arcsec ( s ) + arcsec ( − s ) 0 = arcsin ( x ) + arcsin ( − x ) = arctan ( r ) + arctan ( − r ) = arccsc ( s ) + arccsc ( − s ) {\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc}(s)&&+\operatorname {arccsc}(-s)\\[1.0ex]\end{alignedat}}}
Также, [47] arctan x + arctan 1 x = { π 2 , if x > 0 − π 2 , if x < 0 arccot x + arccot 1 x = { π 2 , if x > 0 3 π 2 , if x < 0 {\displaystyle {\begin{aligned}\arctan x+\arctan {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\-{\frac {\pi }{2}},&{\text{if }}x<0\end{cases}}\\\operatorname {arccot} x+\operatorname {arccot} {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\{\frac {3\pi }{2}},&{\text{if }}x<0\end{cases}}\\\end{aligned}}} arccos 1 x = arcsec x and arcsec 1 x = arccos x {\displaystyle \arccos {\frac {1}{x}}=\operatorname {arcsec} x\qquad {\text{ and }}\qquad \operatorname {arcsec} {\frac {1}{x}}=\arccos x} arcsin 1 x = arccsc x and arccsc 1 x = arcsin x {\displaystyle \arcsin {\frac {1}{x}}=\operatorname {arccsc} x\qquad {\text{ and }}\qquad \operatorname {arccsc} {\frac {1}{x}}=\arcsin x}
Функцию арктангенса можно разложить в ряд: [48] arctan ( n x ) = ∑ m = 1 n arctan x 1 + ( m − 1 ) m x 2 {\displaystyle \arctan(nx)=\sum _{m=1}^{n}\arctan {\frac {x}{1+(m-1)mx^{2}}}}
С помощью функции арктангенса имеем [47] arctan 1 2 = arctan 1 3 + arctan 1 7 . {\displaystyle \arctan {\frac {1}{2}}=\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
Любопытная закономерность, известная как закон Морри , cos 20 ∘ ⋅ cos 40 ∘ ⋅ cos 80 ∘ = 1 8 , {\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}},}
является частным случаем тождества, которое содержит одну переменную: ∏ j = 0 k − 1 cos ( 2 j x ) = sin ( 2 k x ) 2 k sin x . {\displaystyle \prod _{j=0}^{k-1}\cos \left(2^{j}x\right)={\frac {\sin \left(2^{k}x\right)}{2^{k}\sin x}}.}
Сходным образом, sin 20 ∘ ⋅ sin 40 ∘ ⋅ sin 80 ∘ = 3 8 {\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}} x = 20 ∘ {\displaystyle x=20^{\circ }} sin x ⋅ sin ( 60 ∘ − x ) ⋅ sin ( 60 ∘ + x ) = sin 3 x 4 . {\displaystyle \sin x\cdot \sin \left(60^{\circ }-x\right)\cdot \sin \left(60^{\circ }+x\right)={\frac {\sin 3x}{4}}.}
Для случая x = 15 ∘ {\displaystyle x=15^{\circ }} sin 15 ∘ ⋅ sin 45 ∘ ⋅ sin 75 ∘ = 2 8 , sin 15 ∘ ⋅ sin 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\sin 15^{\circ }\cdot \sin 45^{\circ }\cdot \sin 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\sin 15^{\circ }\cdot \sin 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
Для случая x = 10 ∘ {\displaystyle x=10^{\circ }} sin 10 ∘ ⋅ sin 50 ∘ ⋅ sin 70 ∘ = 1 8 . {\displaystyle \sin 10^{\circ }\cdot \sin 50^{\circ }\cdot \sin 70^{\circ }={\frac {1}{8}}.}
То же косинусное тождество cos x ⋅ cos ( 60 ∘ − x ) ⋅ cos ( 60 ∘ + x ) = cos 3 x 4 . {\displaystyle \cos x\cdot \cos \left(60^{\circ }-x\right)\cdot \cos \left(60^{\circ }+x\right)={\frac {\cos 3x}{4}}.}
Сходным образом, cos 10 ∘ ⋅ cos 50 ∘ ⋅ cos 70 ∘ = 3 8 , cos 15 ∘ ⋅ cos 45 ∘ ⋅ cos 75 ∘ = 2 8 , cos 15 ∘ ⋅ cos 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\cos 10^{\circ }\cdot \cos 50^{\circ }\cdot \cos 70^{\circ }&={\frac {\sqrt {3}}{8}},\\\cos 15^{\circ }\cdot \cos 45^{\circ }\cdot \cos 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\cos 15^{\circ }\cdot \cos 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
Сходным образом, tan 50 ∘ ⋅ tan 60 ∘ ⋅ tan 70 ∘ = tan 80 ∘ , tan 40 ∘ ⋅ tan 30 ∘ ⋅ tan 20 ∘ = tan 10 ∘ . {\displaystyle {\begin{aligned}\tan 50^{\circ }\cdot \tan 60^{\circ }\cdot \tan 70^{\circ }&=\tan 80^{\circ },\\\tan 40^{\circ }\cdot \tan 30^{\circ }\cdot \tan 20^{\circ }&=\tan 10^{\circ }.\end{aligned}}}
Следующее, возможно, не так легко обобщить на тождество, содержащее переменные (но см. объяснение ниже): cos 24 ∘ + cos 48 ∘ + cos 96 ∘ + cos 168 ∘ = 1 2 . {\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}
Градусная мера перестает быть более удачной, чем радианная мера, когда мы рассматриваем это тождество с 21 в знаменателе: cos 2 π 21 + cos ( 2 ⋅ 2 π 21 ) + cos ( 4 ⋅ 2 π 21 ) + cos ( 5 ⋅ 2 π 21 ) + cos ( 8 ⋅ 2 π 21 ) + cos ( 10 ⋅ 2 π 21 ) = 1 2 . {\displaystyle \cos {\frac {2\pi }{21}}+\cos \left(2\cdot {\frac {2\pi }{21}}\right)+\cos \left(4\cdot {\frac {2\pi }{21}}\right)+\cos \left(5\cdot {\frac {2\pi }{21}}\right)+\cos \left(8\cdot {\frac {2\pi }{21}}\right)+\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}
Факторы 1, 2, 4, 5, 8, 10 могут прояснить закономерность: это целые числа, меньшие 21 / 2 которые относительно просты (или не имеют общих простых множителей с) 21. Последние несколько примеров являются следствием основного факта о неприводимых круговых многочленах : косинусы являются действительными частями нулей этих многочленов. ; сумма нулей представляет собой функцию Мёбиуса, рассчитанную (в самом последнем случае выше) 21; выше присутствует только половина нулей. Две идентичности, предшествующие последней, возникают таким же образом: 21 заменяется 10 и 15 соответственно.
Другие косинусные тождества включают: [49] 2 cos π 3 = 1 , 2 cos π 5 × 2 cos 2 π 5 = 1 , 2 cos π 7 × 2 cos 2 π 7 × 2 cos 3 π 7 = 1 , {\displaystyle {\begin{aligned}2\cos {\frac {\pi }{3}}&=1,\\2\cos {\frac {\pi }{5}}\times 2\cos {\frac {2\pi }{5}}&=1,\\2\cos {\frac {\pi }{7}}\times 2\cos {\frac {2\pi }{7}}\times 2\cos {\frac {3\pi }{7}}&=1,\end{aligned}}} cos π 3 + cos π 5 × cos 2 π 5 + cos π 7 × cos 2 π 7 × cos 3 π 7 + ⋯ = 1. {\displaystyle \cos {\frac {\pi }{3}}+\cos {\frac {\pi }{5}}\times \cos {\frac {2\pi }{5}}+\cos {\frac {\pi }{7}}\times \cos {\frac {2\pi }{7}}\times \cos {\frac {3\pi }{7}}+\dots =1.}
Многие из этих любопытных личностей проистекают из более общих фактов, таких как следующие: [50] ∏ k = 1 n − 1 sin k π n = n 2 n − 1 {\displaystyle \prod _{k=1}^{n-1}\sin {\frac {k\pi }{n}}={\frac {n}{2^{n-1}}}} ∏ k = 1 n − 1 cos k π n = sin π n 2 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\cos {\frac {k\pi }{n}}={\frac {\sin {\frac {\pi n}{2}}}{2^{n-1}}}.}
Их объединение дает нам ∏ k = 1 n − 1 tan k π n = n sin π n 2 {\displaystyle \prod _{k=1}^{n-1}\tan {\frac {k\pi }{n}}={\frac {n}{\sin {\frac {\pi n}{2}}}}}
Если n — нечетное число ( n = 2 m + 1 {\displaystyle n=2m+1} ∏ k = 1 m tan k π 2 m + 1 = 2 m + 1 {\displaystyle \prod _{k=1}^{m}\tan {\frac {k\pi }{2m+1}}={\sqrt {2m+1}}}
Передаточная функция фильтра нижних частот Баттерворта может быть выражена через полином и полюсы. Установив частоту в качестве частоты среза, можно доказать следующее тождество: ∏ k = 1 n sin ( 2 k − 1 ) π 4 n = ∏ k = 1 n cos ( 2 k − 1 ) π 4 n = 2 2 n {\displaystyle \prod _{k=1}^{n}\sin {\frac {\left(2k-1\right)\pi }{4n}}=\prod _{k=1}^{n}\cos {\frac {\left(2k-1\right)\pi }{4n}}={\frac {\sqrt {2}}{2^{n}}}}
Эффективный способ вычисления π для большого количества цифр основан на следующем тождестве без переменных, предложенном Machin . Это известно как формула типа Машины : π 4 = 4 arctan 1 5 − arctan 1 239 {\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}} Леонарда Эйлера : π 4 = 5 arctan 1 7 + 2 arctan 3 79 {\displaystyle {\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}} тройки Пифагора : π = arccos 4 5 + arccos 5 13 + arccos 16 65 = arcsin 3 5 + arcsin 12 13 + arcsin 63 65 . {\displaystyle \pi =\arccos {\frac {4}{5}}+\arccos {\frac {5}{13}}+\arccos {\frac {16}{65}}=\arcsin {\frac {3}{5}}+\arcsin {\frac {12}{13}}+\arcsin {\frac {63}{65}}.}
Другие включают: [51] [47] π 4 = arctan 1 2 + arctan 1 3 , {\displaystyle {\frac {\pi }{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}},} π = arctan 1 + arctan 2 + arctan 3 , {\displaystyle \pi =\arctan 1+\arctan 2+\arctan 3,} π 4 = 2 arctan 1 3 + arctan 1 7 . {\displaystyle {\frac {\pi }{4}}=2\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
В общем случае для чисел t 1 , ..., t n −1 θ n п -1 k =1 t k π /4, 3 π /4) t n π /2 − θ n θ n t 1 , ..., t n −1 (−1, 1) . В частности, вычисленное t n значения t 1 , ..., t n -1 π 2 = ∑ k = 1 n arctan ( t k ) π = ∑ k = 1 n sgn ( t k ) arccos ( 1 − t k 2 1 + t k 2 ) π = ∑ k = 1 n arcsin ( 2 t k 1 + t k 2 ) π = ∑ k = 1 n arctan ( 2 t k 1 − t k 2 ) , {\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\sum _{k=1}^{n}\arctan(t_{k})\\\pi &=\sum _{k=1}^{n}\operatorname {sgn}(t_{k})\arccos \left({\frac {1-t_{k}^{2}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arcsin \left({\frac {2t_{k}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arctan \left({\frac {2t_{k}}{1-t_{k}^{2}}}\right)\,,\end{aligned}}}
где во всех выражениях, кроме первого, мы использовали формулы касательного полуугла. Первые две формулы работают, даже если одно или несколько значений t k (−1, 1) . Заметим, что если t = p / q (2 t , 1 − t 2 , 1 + т 2 ) значения в приведенных выше формулах пропорциональны тройке Пифагора (2 pq , q 2 − п 2 , q 2 + р 2 ) .
Например, для n = 3 π 2 = arctan ( a b ) + arctan ( c d ) + arctan ( b d − a c a d + b c ) {\displaystyle {\frac {\pi }{2}}=\arctan \left({\frac {a}{b}}\right)+\arctan \left({\frac {c}{d}}\right)+\arctan \left({\frac {bd-ac}{ad+bc}}\right)} a , b , c , d > 0
Евклид показал в книге XIII, предложении 10 своих «Начал» sin 2 18 ∘ + sin 2 30 ∘ = sin 2 36 ∘ . {\displaystyle \sin ^{2}18^{\circ }+\sin ^{2}30^{\circ }=\sin ^{2}36^{\circ }.}
Птолемей использовал это предложение для вычисления некоторых углов в своей таблице хорд в книге I, главе 11 « Альмагеста»
Эти тождества включают тригонометрическую функцию тригонометрической функции: [52]
cos ( t sin x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\sin x)=J_{0}(t)+2\sum _{k=1}^{\infty }J_{2k}(t)\cos(2kx)} sin ( t sin x ) = 2 ∑ k = 0 ∞ J 2 k + 1 ( t ) sin ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\sin x)=2\sum _{k=0}^{\infty }J_{2k+1}(t)\sin {\big (}(2k+1)x{\big )}} cos ( t cos x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ ( − 1 ) k J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\cos x)=J_{0}(t)+2\sum _{k=1}^{\infty }(-1)^{k}J_{2k}(t)\cos(2kx)} sin ( t cos x ) = 2 ∑ k = 0 ∞ ( − 1 ) k J 2 k + 1 ( t ) cos ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\cos x)=2\sum _{k=0}^{\infty }(-1)^{k}J_{2k+1}(t)\cos {\big (}(2k+1)x{\big )}} где J i — функции Бесселя .
α + β + γ = 180°. [ редактировать ] Условное тригонометрическое тождество — это тригонометрическое тождество, которое выполняется, если выполняются заданные условия на аргументы тригонометрических функций. [53] α + β + γ = 180 ∘ , {\displaystyle \alpha +\beta +\gamma =180^{\circ },} tan α + tan β + tan γ = tan α tan β tan γ 1 = cot β cot γ + cot γ cot α + cot α cot β cot ( α 2 ) + cot ( β 2 ) + cot ( γ 2 ) = cot ( α 2 ) cot ( β 2 ) cot ( γ 2 ) 1 = tan ( β 2 ) tan ( γ 2 ) + tan ( γ 2 ) tan ( α 2 ) + tan ( α 2 ) tan ( β 2 ) sin α + sin β + sin γ = 4 cos ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − sin α + sin β + sin γ = 4 cos ( α 2 ) sin ( β 2 ) sin ( γ 2 ) cos α + cos β + cos γ = 4 sin ( α 2 ) sin ( β 2 ) sin ( γ 2 ) + 1 − cos α + cos β + cos γ = 4 sin ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − 1 sin ( 2 α ) + sin ( 2 β ) + sin ( 2 γ ) = 4 sin α sin β sin γ − sin ( 2 α ) + sin ( 2 β ) + sin ( 2 γ ) = 4 sin α cos β cos γ cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α cos β cos γ − 1 − cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α sin β sin γ + 1 sin 2 α + sin 2 β + sin 2 γ = 2 cos α cos β cos γ + 2 − sin 2 α + sin 2 β + sin 2 γ = 2 cos α sin β sin γ cos 2 α + cos 2 β + cos 2 γ = − 2 cos α cos β cos γ + 1 − cos 2 α + cos 2 β + cos 2 γ = − 2 cos α sin β sin γ + 1 sin 2 ( 2 α ) + sin 2 ( 2 β ) + sin 2 ( 2 γ ) = − 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 2 cos 2 ( 2 α ) + cos 2 ( 2 β ) + cos 2 ( 2 γ ) = 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 1 1 = sin 2 ( α 2 ) + sin 2 ( β 2 ) + sin 2 ( γ 2 ) + 2 sin ( α 2 ) sin ( β 2 ) sin ( γ 2 ) {\displaystyle {\begin{aligned}\tan \alpha +\tan \beta +\tan \gamma &=\tan \alpha \tan \beta \tan \gamma \\1&=\cot \beta \cot \gamma +\cot \gamma \cot \alpha +\cot \alpha \cot \beta \\\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)&=\cot \left({\frac {\alpha }{2}}\right)\cot \left({\frac {\beta }{2}}\right)\cot \left({\frac {\gamma }{2}}\right)\\1&=\tan \left({\frac {\beta }{2}}\right)\tan \left({\frac {\gamma }{2}}\right)+\tan \left({\frac {\gamma }{2}}\right)\tan \left({\frac {\alpha }{2}}\right)+\tan \left({\frac {\alpha }{2}}\right)\tan \left({\frac {\beta }{2}}\right)\\\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)\\-\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)\\\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)+1\\-\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)-1\\\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \sin \beta \sin \gamma \\-\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \cos \beta \cos \gamma \\\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \cos \beta \cos \gamma -1\\-\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \cos \beta \cos \gamma +2\\-\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \sin \beta \sin \gamma \\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \cos \beta \cos \gamma +1\\-\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}(2\alpha )+\sin ^{2}(2\beta )+\sin ^{2}(2\gamma )&=-2\cos(2\alpha )\cos(2\beta )\cos(2\gamma )+2\\\cos ^{2}(2\alpha )+\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )&=2\cos(2\alpha )\,\cos(2\beta )\,\cos(2\gamma )+1\\1&=\sin ^{2}\left({\frac {\alpha }{2}}\right)+\sin ^{2}\left({\frac {\beta }{2}}\right)+\sin ^{2}\left({\frac {\gamma }{2}}\right)+2\sin \left({\frac {\alpha }{2}}\right)\,\sin \left({\frac {\beta }{2}}\right)\,\sin \left({\frac {\gamma }{2}}\right)\end{aligned}}}
версинус гаверсинус , коверсинус , В навигации и эксеканс использовались . Например, формула гаверсинуса использовалась для расчета расстояния между двумя точками на сфере. Сегодня они используются редко.
Ядро Дирихле D n ( x ) 1 + 2 cos x + 2 cos ( 2 x ) + 2 cos ( 3 x ) + ⋯ + 2 cos ( n x ) = sin ( ( n + 1 2 ) x ) sin ( 1 2 x ) . {\displaystyle 1+2\cos x+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin \left({\frac {1}{2}}x\right)}}.}
Свертка интегрируемой любой функции периода 2 π {\displaystyle 2\pi } n {\displaystyle n} меры или обобщенной функции .
Если мы установим t = tan x 2 , {\displaystyle t=\tan {\frac {x}{2}},} [54] sin x = 2 t 1 + t 2 ; cos x = 1 − t 2 1 + t 2 ; e i x = 1 + i t 1 − i t ; d x = 2 d t 1 + t 2 , {\displaystyle \sin x={\frac {2t}{1+t^{2}}};\qquad \cos x={\frac {1-t^{2}}{1+t^{2}}};\qquad e^{ix}={\frac {1+it}{1-it}};\qquad dx={\frac {2\,dt}{1+t^{2}}},} e i x = cos x + i sin x , {\displaystyle e^{ix}=\cos x+i\sin x,} цис x
Когда эта замена t {\displaystyle t} загара x / 2 используется в исчислении , отсюда следует, что sin x {\displaystyle \sin x} 2 т / 1 + т 2 cos x {\displaystyle \cos x} 1 - т 2 / 1 + т 2 d x заменяется на 2 д т / 1 + т 2 sin x {\displaystyle \sin x} cos x {\displaystyle \cos x} t {\displaystyle t} первообразные .
cos θ 2 ⋅ cos θ 4 ⋅ cos θ 8 ⋯ = ∏ n = 1 ∞ cos θ 2 n = sin θ θ = sinc θ . {\displaystyle \cos {\frac {\theta }{2}}\cdot \cos {\frac {\theta }{4}}\cdot \cos {\frac {\theta }{8}}\cdots =\prod _{n=1}^{\infty }\cos {\frac {\theta }{2^{n}}}={\frac {\sin \theta }{\theta }}=\operatorname {sinc} \theta .}
^ Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 4, уравнение 4.3.45» . Справочник по математическим функциям с формулами, графиками и математическими таблицами ИСБН 978-0-486-61272-0 LCCN 64-60036 . МР 0167642 . LCCN 65-12253 . ^ Селби 1970 , с. 188 ^ Абрамовиц и Стегун, с. 72, 4.3.13–15 ^ Абрамовиц и Стегун, с. 72, 4.3.7–9 ^ Абрамовиц и Стегун, с. 72, 4.3.16 ↑ Перейти обратно: Перейти обратно: а б с д Вайсштейн, Эрик В. «Формулы тригонометрического сложения» . Математический мир ^ Абрамовиц и Стегун, с. 72, 4.3.17 ^ Абрамовиц и Стегун, с. 72, 4.3.18 ↑ Перейти обратно: Перейти обратно: а б «Угловая сумма и разностные тождества» . www.milefoot.com . Проверено 12 октября 2019 г. ^ Абрамовиц и Стегун, с. 72, 4.3.19 ^ Абрамовиц и Стегун, с. 80, 4.4.32 ^ Абрамовиц и Стегун, с. 80, 4.4.33 ^ Абрамовиц и Стегун, с. 80, 4.4.34 ^ Бронштейн, Мануэль (1989). «Упрощение реальных элементарных функций». В Гонне, GH (ред.). Труды Международного симпозиума ACM- SIGSAM 1989 по символьным и алгебраическим вычислениям . ISSAC '89 (Портленд, США, Орегон, 1989–07). Нью-Йорк: ACM . стр. 207–211. дои : 10.1145/74540.74566 . ISBN 0-89791-325-6 ^ Майкл Харди. (2016). «О касательных и секансах бесконечных сумм». The American Mathematical Monthly , том 123, номер 7, 701–703. https://doi.org/10.4169/amer.math.monthly.123.7.701 ^ Харди, Майкл (2016). «О касательных и секансах бесконечных сумм» . Американский математический ежемесячник . 123 (7): 701–703. doi : 10.4169/amer.math.monthly.123.7.701 . ↑ Перейти обратно: Перейти обратно: а б «Синус, косинус и теорема Птолемея» . ↑ Перейти обратно: Перейти обратно: а б Вайсштейн, Эрик В. «Формулы нескольких углов» . Математический мир ^ Абрамовиц и Стегун, с. 74, 4.3.48 ↑ Перейти обратно: Перейти обратно: а б Селби 1970 , стр. 190 ^ Вайсштейн, Эрик В. «Формулы нескольких углов» . mathworld.wolfram.com . Проверено 6 февраля 2022 г. ^ Уорд, Кен. «Многоугольная рекурсивная формула» . Страницы математики Кена Уорда . ↑ Перейти обратно: Перейти обратно: а б Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 4, уравнения 4.3.20-22» . Справочник по математическим функциям с формулами, графиками и математическими таблицами ИСБН 978-0-486-61272-0 LCCN 64-60036 . МР 0167642 . LCCN 65-12253 . ↑ Перейти обратно: Перейти обратно: а б Вайсштейн, Эрик В. «Формулы половинного угла» . Математический мир ^ Абрамовиц и Стегун, с. 72, 4.3.24–26 ^ Вайсштейн, Эрик В. «Формулы двойного угла» . Математический мир ^ Абрамовиц и Стегун, с. 72, 4.3.27–28 ^ Абрамовиц и Стегун, с. 72, 4.3.31–33 ^ Ивс, Ховард (1990). Введение в историю математики (6-е изд.). Филадельфия: Паб Saunders College. п. 309. ИСБН 0-03-029558-0 OCLC 20842510 . ^ Абрамовиц и Стегун, с. 72, 4.3.34–39 ^ Джонсон, Уоррен П. (апрель 2010 г.). «Тригонометрические тождества по-эрмитски». Американский математический ежемесячник 117 (4): 311–327. дои : 10.4169/000298910x480784 . S2CID 29690311 . ^ «Идентификация продукта под разными углами» . ^ Апостол, ТМ (1967) Исчисление. 2-е издание. Нью-Йорк, Нью-Йорк, Уайли. Стр. 334-335. ↑ Перейти обратно: Перейти обратно: а б Вайсштейн, Эрик В. «Теорема гармонического сложения» . Математический мир ^ Ортис Муньис, Эдди (февраль 1953 г.). «Метод вывода различных формул электростатики и электромагнетизма с использованием тригонометрических тождеств Лагранжа». Американский журнал физики . 21 (2): 140. Бибкод : 1953AmJPh..21..140M . дои : 10.1119/1.1933371 . ^ Агарвал, Рави П.; О'Риган, Донал (2008). Обыкновенные дифференциальные уравнения и уравнения в частных производных: со специальными функциями, рядами Фурье и краевыми задачами ИСБН 978-0-387-79146-3 Выдержка со страницы 185 ^ Джеффри, Алан; Дай, Хуэй-хуэй (2008). «Раздел 2.4.1.6». Справочник по математическим формулам и интегралам (4-е изд.). Академическая пресса. ISBN 978-0-12-374288-9 ^ Фэй, Темпл Х.; Клопперс, П. Хендрик (2001). «Феномен Гиббса» . Международный журнал математического образования в области науки и технологий . 32 (1): 73–89. дои : 10.1080/00207390117151 . ^ Абрамовиц и Стегун, с. 74, 4.3.47 ^ Абрамовиц и Стегун, с. 71, 4.3.2 ^ Абрамовиц и Стегун, с. 71, 4.3.1 ^ Абрамовиц и Стегун, с. 80, 4.4.26–31 ^ Абрамовиц и Стегун, с. 74, 4.3.65–66 ^ Абрамовиц и Стегун, с. 75, 4.3.89–90 ^ Абрамовиц и Стегун, с. 85, 4.5.68–69 ^ Абрамовиц и Стегун 1972 , с. 73, 4.3.45 ↑ Перейти обратно: Перейти обратно: а б с Ву, Рекс Х. «Доказательство без слов: арктангенсальная идентичность Эйлера», Mathematics Magazine 77 (3), июнь 2004 г., стр. 189. ^ С. М. Абраров, Р. К. Джагпал, Р. Сиддики и Б. М. Куайн (2021), «Алгоритмическое определение большого целого числа в двухчленной машинной формуле для π», Математика , 9 (17), 2162, arXiv : 2107.01027 doi : 10.3390/math9172162 {{citation }}: CS1 maint: несколько имен: список авторов ( ссылка ) ^ Скромный, Стив (ноябрь 2004 г.). «Бабушкина личность». Математический вестник . 88 : 524–525. дои : 10.1017/s0025557200176223 . S2CID 125105552 . ^ Вайсштейн, Эрик В. «Синус» . Математический мир ^ Харрис, Эдвард М. «Суммы арктангенсов», Роджер Б. Нельсон, « Доказательства без слов» (1993, Математическая ассоциация Америки), стр. 39. ^ Милтон Абрамовиц и Ирен Стеган, Справочник по математическим функциям с формулами, графиками и математическими таблицами , Dover Publications , Нью-Йорк, 1972, формулы 9.1.42–9.1.45 ^ Эр. К.С. Джоши, ИИТ Кришны МАТЕМАТИКА . Кришна Пракашан Медиа. Меерут, Индия. страница 636. ^ Абрамовиц и Стегун, с. 72, 4.3.23 Абрамовиц, Милтон ; Стегун, Ирен А. , ред. (1972). Справочник по математическим функциям с формулами, графиками и математическими таблицами Dover Publications . ISBN 978-0-486-61272-0 Нильсен, Кай Л. (1966), Логарифмические и тригонометрические таблицы для пяти мест (2-е изд.), Нью-Йорк: Barnes & Noble , LCCN 61-9103 Селби, Сэмюэл М., изд. (1970), Стандартные математические таблицы (18-е изд.), The Chemical Rubber Co. 


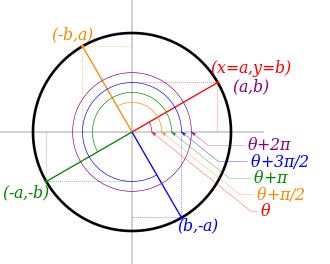


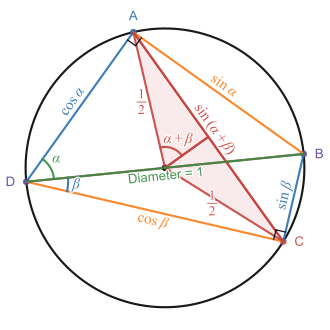


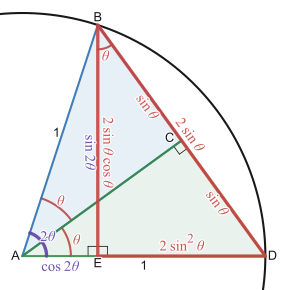
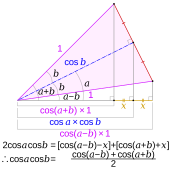
























































































































![{\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta)=\operatorname {sgn}(\csc \theta)&={\begin{cases}+1& {\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0 ,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{ \text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}} \ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2} }\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases }+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta < {\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text {или}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\ tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cc79239a0fcdfb53b132d75a93474e9e6d5ba0)

![{\displaystyle ({-\пи},\пи],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122328145a5f3a4162d21b4fbb5f4d1149932d2b)






































![{\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _ {i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k }\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1927ae2be96f5156e18813a20486fdb0ff72f1)
![{\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr)}&={\frac {{\sin }{\bigl (} \sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\ theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd} }\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\ \left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\ geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left| A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5} -\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i} {\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02567417a5a013481366384787e518cd74c68be)
![{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}= {\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2 }}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_ {3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2} x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac { e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_ {3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4 }+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_ {2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}}, \end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9196b8ab5e0aef6cf7d7fec7d7546f2a6e7d2f)
![{\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \ theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{ i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24f2b169fbe11608507c63f5bb728e03b2b4957)


![{\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma)&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \ beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e082e69aab7a9c782f590f3a93262ba3101899b7)




























































![{\displaystyle {\begin{aligned}\sin {\frac {\theta}{2}}&=\operatorname {sgn}\left(\sin {\frac {\theta}{2}}\right){\ sqrt {\frac{1-\cos\theta}{2}}}\\[3pt]\cos{\frac{\theta}{2}}&=\operatorname{sgn}\left(\cos{\frac {\theta}{2}}\right){\sqrt {\frac{1+\cos\theta}{2}}}\\[3pt]\tan{\frac{\theta}{2}}&= {\frac {1-\cos\theta}{\sin\theta}}={\frac {\sin\theta}{1+\cos\theta}}=\csc\theta -\cot \theta ={\ frac {\tan\theta}{1+\sec {\theta}}}\\[6mu]&=\operatorname{sgn}(\sin\theta){\sqrt{\frac{1-\cos\theta} {1+\cos\theta}}}={\frac {-1+\operatorname{sgn}(\cos\theta){\sqrt{1+\tan^{2}\theta}}}{\tan\ theta }}\\[3pt]\cot {\frac{\theta}{2}}&={\frac{1+\cos\theta}{\sin\theta}}={\frac{\sin\theta }{1-\cos\theta}}=\csc\theta+\cot\theta=\operatorname{sgn}(\sin\theta){\sqrt{\frac{1+\cos\theta}{1-\ cos \theta}}}\\\sec {\frac{\theta}{2}}&=\operatorname{sgn}\left(\cos{\frac{\theta}{2}}\right){\sqrt { \frac{2}{1+\cos\theta}}}\\\csc{\frac{\theta}{2}}&=\operatorname{sgn}\left(\sin{\frac{\theta} { 2}}\right){\sqrt {\frac {2}{1-\cos\theta}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d104c73c4b28f1dd7bfa5d2b0c7207c68cd87)
![{\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta}{2}} &={\frac {\sin \eta \pm \sin \theta}{\cos \eta +\ cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta}{1+\sin \theta}}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta}{2}}\right|}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639270245e163f1afa8682ac8aa12086db43dce1)








![{\displaystyle {\begin{aligned}\tan {\frac {\theta}{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1- \cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin\ theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta}{2}}+{\frac {\pi}{4}}\right) &=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1 -\tan {\frac {\theta}{2}}\right|}{\left|1+\tan {\frac {\theta}{2}}\right|}}\\[5pt]\tan { \frac {\theta}{2}}&={\frac {\tan \theta}{1+{\sqrt {1+\tan^{2}\theta}}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi}{2}},{\tfrac {\pi}{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cab50a58d64b8c3341fb4f7646888bbbc67ea0c)
![{\displaystyle {\begin{aligned}\cot {\frac {\theta}{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+ \cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos\theta}{\sin\theta}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c9be831a310f112ffc6e5790bc705dc7b070b87)
















































![{\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e \in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[6pt]&{\text{where }}e=(e_{ 1},\ldots ,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce2126a8ded0d0c92cf2bc4e9386c34430513c4b)







































![{\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \ left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1) }{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c850aa2dd7cc306d87d5d68d5802cab64f8572a0)



































![{\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty }\left(1- {\frac {x^{2}}{\pi ^{2}n ^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2} \left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\[10mu]\sinh x&=x\prod _ {n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _ {n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right )\!{\vphantom {)}}^{2}}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d43e1176a38b1e6b653837eb782ae79735783ac)








![{\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+ \operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\ arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s )\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc }(s)&&+\operatorname {arccsc}(-s)\\[1.0ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/839db041f421b4af5890106450e2b4d3e9e183d4)
















































