Ромбический триаконтаэдр

Ромбический триаконтаэдр
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Каталонский солид
Диаграмма Кокстера
Обозначение Конвея	ДжейДи
Тип лица	В3.5.3.5 ромб
Лица	30
Края	60
Вершины	32
Вершины по типу	20{3}+12{5}
Группа симметрии	I h , H 3 , [5,3], (*532)
Группа вращения	Я, [5,3] + , (532)
Двугранный угол	144°
Характеристики	выпуклый, грани-переходный изоэдр , изотоксал , зоноэдр
Икосододекаэдр ( двойной многогранник )	Сеть

3D модель ромбического триаконтаэдра

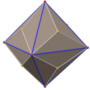
Ромбический триаконтаэдр , иногда называемый просто триаконтаэдром , поскольку это наиболее распространенный тридцатигранный многогранник , представляет собой выпуклый многогранник с 30 ромбическими гранями . Он имеет 60 ребер и 32 вершины двух типов. Это каталонское тело и многогранник икосододекаэдра . двойственный Это зоноэдр .

Грань ромботриаконтаэдра. Длина диагоналей находятся в золотом сечении .

Эта анимация показывает преобразование куба в ромбический триаконтаэдр путем разделения квадратных граней на 4 квадрата и разделения средних ребер на новые ромбические грани.

Отношение длинной диагонали к короткой диагонали каждой грани в точности равно сечению золотому φ , так что острые углы на каждой грани равны 2 арктансу ( ⁠ 1 / φ ⁠ ) = arctan(2) или примерно 63,43°. Полученный таким образом ромб называется золотым ромбом .

Будучи двойственным архимедовым телом , ромбический триаконтаэдр является транзитивным по граням , что означает, что группа симметрии твердого тела действует транзитивно на наборе граней. Это означает, что для любых двух граней A и B происходит вращение или отражение в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B. твердого тела ,

Ромбический триаконтаэдр в некоторой степени особенный, поскольку он является одним из девяти выпуклых многогранников с транзитивными ребрами , остальные — пять Платоновых тел , кубооктаэдр , икосододекаэдр и ромбический додекаэдр .

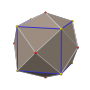
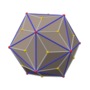
Ромбический триаконтаэдр интересен еще и тем, что его вершины включают в себя расположение четырех Платоновых тел. Он содержит десять тетраэдров , пять кубов , икосаэдр и додекаэдр . В центрах граней находятся пять октаэдров .

Его можно сделать из усеченного октаэдра , разделив шестиугольные грани на три ромба:

Топологический ромбический триаконтаэдр в усеченном октаэдре.

Декартовы координаты

Пусть φ — золотое сечение . 12 точек, заданных (0, ±1, ± φ ), и циклические перестановки этих координат являются вершинами правильного икосаэдра . Его двойственный правильный додекаэдр , ребра которого пересекают ребра икосаэдра под прямым углом, имеет в качестве вершин 8 точек (±1, ±1, ±1) вместе с 12 точками (0, ± φ , ±1). ⁠ 1 / φ ⁠ ) и циклические перестановки этих координат. Все 32 точки вместе являются вершинами ромботриаконтаэдра с центром в начале координат. Длина его ребер равна √ 3 – φ ≈ 1,175 570 504 58 . Его грани имеют диагонали длиной 2 и ⁠ 2 / φ ⁠ .

Размеры

Если длина ребра ромботриаконтаэдра равна , площадь поверхности, объем, радиус ( вписанной сферы касательной к каждой из граней ромботриаконтаэдра) и средний радиус, который касается середины каждого ребра, равны:

${\begin{aligned}S&=12{\sqrt {5}}\,a^{2}&&\approx 26.8328a^{2}\\[6px]V&=4{\sqrt {5+2{\sqrt {5}}}}\,a^{3}&&\approx 12.3107a^{3}\\[6px]r_{\mathrm {i} }&={\frac {\varphi ^{2}}{\sqrt {1+\varphi ^{2}}}}\,a={\sqrt {1+{\frac {2}{\sqrt {5}}}}}\,a&&\approx 1.37638a\\[6px]r_{\mathrm {m} }&=\left(1+{\frac {1}{\sqrt {5}}}\right)\,a&&\approx 1.44721a\end{aligned}}$

где φ — золотое сечение .

Сфера . касается граней в их центрах тяжести Короткие диагонали принадлежат только ребрам вписанного правильного додекаэдра, а длинные диагонали входят только в рёбра вписанного икосаэдра.

Диссекция

Ромбический триаконтаэдр можно разрезать на 20 золотых ромбоэдров : 10 острых и 10 тупых.

10	10
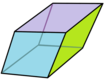Острая форма	Тупая форма

Ортогональные проекции

Ромбический триаконтаэдр имеет четыре положения симметрии: два с центром в вершинах, одно в середине грани и одно в середине ребра. В проекцию «10» встроены «толстый» ромб и «тонкий» ромб, которые соединяются вместе, образуя непериодическую мозаику, часто называемую мозаикой Пенроуза .

Ортогональные проекции

Проективный симметрия	[2]	[2]	[6]	[10]
Изображение
Двойной изображение

Звездочки

Ромбический шестиконтаэдр

Пример звездочек ромботриаконтаэдра.

Дополнительная информация: Ромбический шестиконтаэдр.

Ромбический триаконтаэдр имеет 227 полностью закрепленных звездочек. Еще одна звездчатая форма ромбического триаконтаэдра — соединение пяти кубов . Общее число звездочек ромбического триаконтаэдра составляет 358 833 097 .

Связанные многогранники

показывать Семейство однородных икосаэдрических многогранников.
Symmetry: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Этот многогранник является частью последовательности ромбических многогранников и мозаик с [ n , 3] симметрией группы Кокстера . Куб можно рассматривать как ромбический шестигранник, где ромбы также являются прямоугольниками.

показывать Мутации симметрии двойственных квазирегулярных мозаик: V(3.n) 2
*n32	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

• 
  Сферический ромбический триаконтаэдр
• 
  Ромбический триаконтаэдр с вписанным тетраэдром (красный) и кубом (желтый).
  (Нажмите здесь, чтобы увидеть вращающуюся модель)
• 
  Ромбический триаконтаэдр с вписанными додекаэдром (синий) и икосаэдром (фиолетовый).
  (Нажмите здесь, чтобы увидеть вращающуюся модель)
• 
  Полностью усеченный ромбический триаконтаэдр

Использование

Пример использования ромботриаконтаэдра в конструкции светильника

Датский дизайнер Хольгер Стрём использовал ромбический триаконтаэдр в качестве основы для конструкции своей сборной лампы IQ-light (IQ означает «переплетающиеся четырехугольники»).

STL-модель ромботриаконтаэдрической коробки, состоящей из шести панелей вокруг кубического отверстия – увеличьте масштаб модели, чтобы увидеть отверстие изнутри.

Столяр Джейн Костик строит коробки в форме ромботриаконтаэдра. Простая конструкция основана на неочевидной связи между ромбическим триаконтаэдром и кубом.

«Шар ударов» Роджера фон Оеха имеет форму ромбического триаконтаэдра.

Ромбический триаконтаэдр используется как « d30 тридцатигранный кубик », иногда полезный в некоторых ролевых играх или других местах.

См. также

• Золотой ромб
• Ромбическая плитка
• Усеченный ромбический триаконтаэдр

Ссылки

• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN  0-486-23729-Х . (Раздел 3-9)
• Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN  978-0-521-54325-5 , MR   0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им, стр. 22, Ромбический триаконтаэдр)
• Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, ISBN   978-1-56881-220-5 [2] (Глава 21, Названия архимедовых и каталанских многогранников и мозаик, стр. 285, Ромбический триаконтаэдр)

Внешние ссылки

• Вайсштейн, Эрик В. , « Ромбический триаконтаэдр » (« каталонское тело ») в MathWorld .
• Ромбический триаконтраэдр – интерактивная модель многогранника
• Многогранники виртуальной реальности – Энциклопедия многогранников
• Звездочки ромбического триаконтаэдра
• Глобус EarthStar – картографическая проекция ромбического триаконтаэдра
• IQ-light — лампа датского дизайнера Хольгера Стрёма.
• Создайте свой собственный. Архивировано 17 июля 2007 г. в Wayback Machine.
• деревянная конструкция коробки из ромбического триаконтаэдра - работа столяра Джейн Костик.
• 120 ромбических триаконтаэдров , 30+12 ромбических триаконтаэдров и 12 ромбических триаконтаэдров , автор Шандор Кабаи, Демонстрационный проект Вольфрама
• Змея, нарисованная на ромботриаконтаэдре .