Статистика Бозе – Эйнштейна

В квантовой статистике статистика Бозе-Эйнштейна ( статистика B-E ) описывает один из двух возможных способов, которыми совокупность невзаимодействующих идентичных частиц может занимать набор доступных дискретных энергетических состояний в термодинамическом равновесии . Агрегация частиц в одном и том же состоянии, характерная для частиц, подчиняющихся статистике Бозе-Эйнштейна, объясняет когезионное течение лазерного света и ползучесть сверхтекучего гелия без трения . Теорию такого поведения разработал (1924–25) Сатьендра Натх Бозе , который признал, что совокупность одинаковых и неразличимых частиц может быть распределена таким образом. Позднее эта идея была принята и развита Альбертом Эйнштейном в сотрудничестве с Бозе.

Статистика Бозе-Эйнштейна применима только к частицам, которые не подчиняются ограничениям принципа исключения Паули . Частицы, подчиняющиеся статистике Бозе-Эйнштейна, называются бозонами и имеют целые значения спина . Напротив, частицы, которые подчиняются статистике Ферми-Дирака, называются фермионами и имеют полуцелые спины.

Равновесные тепловые распределения для частиц с целым спином (бозоны), полуцелыми спинами (фермионы) и классическими (бесспиновыми) частицами. Средняя заполняемость $\langle n\rangle$ показано в зависимости от энергии $\epsilon$ относительно химического потенциала системы $\mu$, где $T$ - температура системы, и $k_{\text{B}}$ — постоянная Больцмана.

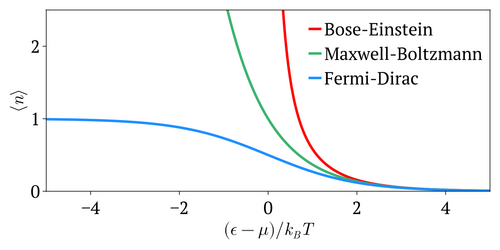
Распределение Бозе – Эйнштейна

При низких температурах бозоны ведут себя иначе, чем фермионы (которые подчиняются статистике Ферми-Дирака ), поскольку неограниченное их количество может «конденсироваться» в одно и то же энергетическое состояние. Это, казалось бы, необычное свойство также приводит к возникновению особого состояния вещества – конденсата Бозе-Эйнштейна . Статистика Ферми-Дирака и Бозе-Эйнштейна применяется, когда важны квантовые эффекты и частицы « неразличимы ». Квантовые эффекты возникают, если концентрация частиц удовлетворяет $${\frac {N}{V}}\geq n_{\text{q}},$$ где N — число частиц, V — объем, а n _q — концентрация квантов , для которой расстояние между частицами равно тепловой длине волны де Бройля , так что волновые функции частиц практически не перекрываются.

Статистика Ферми-Дирака применима к фермионам (частицам, подчиняющимся принципу исключения Паули ), а статистика Бозе-Эйнштейна применима к бозонам . Поскольку концентрация квантов зависит от температуры, большинство систем при высоких температурах подчиняются классическому пределу (Максвелла-Больцмана), если только они не обладают очень высокой плотностью, как у белого карлика . И Ферми-Дирак, и Бозе-Эйнштейн становятся статистиками Максвелла-Больцмана при высокой температуре или при низкой концентрации.

Статистика Бозе-Эйнштейна была введена для фотонов в 1924 году Бозе и обобщена на атомы Эйнштейном в 1924–25 годах.

Ожидаемое количество частиц в энергетическом состоянии i для статистики Бозе – Эйнштейна равно:

${\bar {n}}_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}-1}}$

с ε _i > µ и где n _i — число заполнения (количество частиц) в состоянии i , $g_{i}$ — вырождение уровня энергии i , ε _i — энергия - го i состояния, μ — химический потенциал (ноль для фотонного газа ), k _B — постоянная Больцмана , а T — абсолютная температура .

Дисперсия этого распределения $V(n)$ рассчитывается непосредственно из приведенного выше выражения для среднего числа. $$V(n)=kT{\frac {\partial }{\partial \mu }}{\bar {n}}_{i}=\langle n\rangle (1+\langle n\rangle )={\bar {n}}+{\bar {n}}^{2}$$

Для сравнения: среднее число фермионов с энергией $\varepsilon _{i}$ имеет распределение частиц по энергии Ферми – Дирака аналогичный вид: $${\bar {n}}_{i}(\varepsilon _{i})={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}+1}}.$$

Как упоминалось выше, как распределение Бозе-Эйнштейна, так и распределение Ферми-Дирака приближаются к распределению Максвелла-Больцмана в пределе высокой температуры и низкой плотности частиц без необходимости каких-либо специальных предположений:

• В пределе малой плотности частиц ${\bar {n}}_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}\pm 1}}\ll 1$, поэтому $e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}\pm 1\gg 1$ или эквивалентно $e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}\gg 1$. В этом случае ${\bar {n}}_{i}\approx {\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}}}={\frac {1}{Z}}e^{-(\varepsilon _{i}-\mu )/k_{\text{B}}T}$, что является результатом статистики Максвелла – Больцмана.
• В пределе высоких температур частицы распределены в большом диапазоне значений энергии, поэтому заселенность каждого состояния (особенно высокоэнергетических с $\varepsilon _{i}-\mu \gg k_{\text{B}}T$) снова очень мала, ${\bar {n}}_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}\pm 1}}\ll 1$. Это снова сводится к статистике Максвелла – Больцмана.

Помимо сведения к распределению Максвелла–Больцмана в пределе больших $T$ и низкой плотности статистика Бозе-Эйнштейна также сводится к закона Рэлея-Джинса для состояний с низкой энергией с распределению $\varepsilon _{i}-\mu \ll k_{\text{B}}T$, а именно $${\begin{aligned}{\bar {n}}_{i}&={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}-1}}\\&\approx {\frac {g_{i}}{(\varepsilon _{i}-\mu )/k_{\text{B}}T}}={\frac {g_{i}k_{\text{B}}T}{\varepsilon _{i}-\mu }}.\end{aligned}}$$

История

Владислав Натансон в 1911 году пришел к выводу, что закон Планка требует неразличимости «единиц энергии», хотя он не формулировал это с точки зрения квантов света Эйнштейна.

) лекцию Читая в Университете Дакки (на территории тогдашней Британской Индии , а ныне Бангладеш о теории радиации и ультрафиолетовой катастрофы , Сатьендра Нат Бозе намеревался показать своим студентам, что современная теория неадекватна, поскольку она предсказывает результаты. не соответствует экспериментальным результатам. Во время этой лекции Бозе допустил ошибку в применении теории, которая неожиданно дала предсказание, согласовавшееся с экспериментом. Ошибка была простой ошибкой — подобно утверждению, что при подбрасывании двух честных монет в одной трети случаев выпадет два орла, — которая показалась бы явно неправильной любому, кто имеет базовое понимание статистики (примечательно, что эта ошибка напоминала знаменитую ошибку Д. 'Аламбер известен по своей Croix ou Pile. статье ). Однако предсказанные результаты совпали с экспериментом, и Бозе понял, что это, возможно, не ошибка. Впервые он занял позицию, согласно которой распределение Максвелла-Больцмана не будет верным для всех микроскопических частиц во всех масштабах. Таким образом, он исследовал вероятность нахождения частиц в различных состояниях в фазовом пространстве, где каждое состояние представляет собой небольшой участок с фазовым объемом h. ³ , а положение и импульс частиц не разделяются отдельно, а рассматриваются как одна переменная.

Бозе адаптировал эту лекцию в небольшую статью под названием «Закон Планка и гипотеза световых квантов». и представил его в «Философский журнал» . Однако заключение рецензента было отрицательным, и статья была отклонена. Не испугавшись, он отправил рукопись Альберту Эйнштейну с просьбой опубликовать ее в Zeitschrift für Physik . Эйнштейн немедленно согласился, лично перевел статью с английского на немецкий (ранее Бозе перевел статью Эйнштейна по общей теории относительности с немецкого на английский) и позаботился о ее публикации. Теория Бозе завоевала уважение, когда Эйнштейн отправил свою статью в поддержку теории Бозе в Zeitschrift für Physik с просьбой опубликовать их вместе. Газета вышла в 1924 году.

Причина, по которой Бозе дал точные результаты, заключалась в том, что, поскольку фотоны неотличимы друг от друга, нельзя рассматривать любые два фотона, имеющие равные квантовые числа (например, поляризацию и вектор импульса), как два различных идентифицируемых фотона. Первоначально Бозе имел коэффициент 2 для возможных спиновых состояний, но Эйнштейн заменил его на поляризацию. По аналогии, если бы в альтернативной вселенной монеты вели себя как фотоны и другие бозоны, вероятность появления двух орлов действительно составляла бы одну треть, как и вероятность получения орла и решки, которая равна половине для обычные (классические, различимые) монеты. «Ошибка» Бозе приводит к тому, что сейчас называется статистикой Бозе-Эйнштейна.

Бозе и Эйнштейн распространили эту идею на атомы, и это привело к предсказанию существования явления, которое стало известно как конденсат Бозе-Эйнштейна, плотное скопление бозонов (которые представляют собой частицы с целым спином, названные в честь Бозе), что было продемонстрировано существуют экспериментально в 1995 году.

Вывод

Вывод из микроканонического ансамбля

В микроканоническом ансамбле рассматривается система с фиксированными энергией, объемом и числом частиц. Возьмем систему, состоящую из ${\textstyle N=\sum _{i}n_{i}}$ одинаковые бозоны, $n_{i}$ из них обладают энергией $\varepsilon _{i}$ и распределяются по $g_{i}$ уровни или состояния с одинаковой энергией $\varepsilon _{i}$, то есть $g_{i}$ это вырождение, связанное с энергией $\varepsilon _{i}$ полной энергии ${\textstyle E=\sum _{i}n_{i}\varepsilon _{i}}$. Расчет количества мероприятий $n_{i}$ частицы распределены между $g_{i}$ Состояния – это проблема комбинаторики . Поскольку здесь частицы неразличимы в квантовомеханическом контексте, количество способов их расположения $n_{i}$ частицы в $g_{i}$ коробки (для $i$энергетический уровень) будет (см. изображение):

Изображение представляет собой одно из возможных распределений бозонных частиц в разных ящиках. Перегородки ящиков (зеленые) можно перемещать, чтобы изменить размер ящиков и, как следствие, количество бозонов, которые может содержать каждый ящик.

$$w_{i,{\text{BE}}}={\frac {(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!}}=C_{n_{i}}^{n_{i}+g_{i}-1},$$ где $C_{k}^{m}$ есть k -комбинация множества из m элементов. Полное число расположений в ансамбле бозонов представляет собой просто произведение биномиальных коэффициентов. $C_{n_{i}}^{n_{i}+g_{i}-1}$ выше по всем энергетическим уровням, т.е. $$W_{\text{BE}}=\prod _{i}w_{i,{\text{BE}}}=\prod _{i}{\frac {(n_{i}+g_{i}-1)!}{(g_{i}-1)!n_{i}!}},$$

Максимальное количество мероприятий, определяющих соответствующий номер занятия $n_{i}$ получается путем максимизации энтропии или, что то же самое, установки $\mathrm {d} (\ln W_{\text{BE}})=0$ и принимая дополнительные условия ${\textstyle N=\sum n_{i},E=\sum _{i}n_{i}\varepsilon _{i}}$ (как множители Лагранжа ). Результат для $n_{i}\gg 1$, $g_{i}\gg 1$, $n_{i}/g_{i}=O(1)$ представляет собой распределение Бозе-Эйнштейна.

Вывод из великого канонического ансамбля

Распределение Бозе-Эйнштейна, применимое только к квантовой системе невзаимодействующих бозонов, естественным образом выводится из большого канонического ансамбля без каких-либо приближений. В этом ансамбле система способна обмениваться энергией и обмениваться частицами с резервуаром (температура Т и химический потенциал ц, фиксируемые резервуаром).

Благодаря невзаимодействующему качеству каждый доступный одночастичный уровень (с уровнем энергии ϵ ) образует отдельную термодинамическую систему, контактирующую с резервуаром. То есть количество частиц внутри всей системы , занимающих данное одночастичное состояние, образует подансамбль, который также является большим каноническим ансамблем; следовательно, его можно проанализировать посредством построения большой статистической суммы .

Каждое одночастичное состояние имеет фиксированную энергию. $\varepsilon$. Поскольку подансамбль, связанный с одночастичным состоянием, варьируется только в зависимости от числа частиц, ясно, что полная энергия подансамбля также прямо пропорциональна числу частиц в одночастичном состоянии; где $N$ - число частиц, тогда полная энергия подансамбля будет равна $N\varepsilon$. Начнем со стандартного выражения для большой функции распределения и заменим $E$ с $N\varepsilon$, большая статистическая сумма принимает вид $${\mathcal {Z}}=\sum _{N}\exp((N\mu -N\varepsilon )/k_{\text{B}}T)=\sum _{N}\exp(N(\mu -\varepsilon )/k_{\text{B}}T)$$

Эта формула применима как к фермионным, так и к бозонным системам. Статистика Ферми-Дирака возникает при рассмотрении эффекта принципа исключения Паули : хотя число фермионов, занимающих одно и то же одночастичное состояние, может быть только 1 или 0, количество бозонов, занимающих одночастичное состояние, может быть любым целым числом. Таким образом, большую статистическую сумму для бозонов можно рассматривать как геометрическую серию и оценивать ее следующим образом: $${\begin{aligned}{\mathcal {Z}}&=\sum _{N=0}^{\infty }\exp(N(\mu -\varepsilon )/k_{\text{B}}T)=\sum _{N=0}^{\infty }[\exp((\mu -\varepsilon )/k_{\text{B}}T)]^{N}\\&={\frac {1}{1-\exp((\mu -\varepsilon )/k_{\text{B}}T)}}.\end{aligned}}$$

Заметим, что геометрический ряд сходится только в том случае, если $e^{(\mu -\varepsilon )/k_{\text{B}}T}<1$, включая случай, когда $\varepsilon =0$. Это означает, что химический потенциал бозе-газа должен быть отрицательным, т. е. $\mu <0$, тогда как ферми-газу разрешено принимать как положительные, так и отрицательные значения химического потенциала.

Среднее число частиц для этого одночастичного подсостояния определяется выражением $$\langle N\rangle =k_{\text{B}}T{\frac {1}{\mathcal {Z}}}\left({\frac {\partial {\mathcal {Z}}}{\partial \mu }}\right)_{V,T}={\frac {1}{\exp((\varepsilon -\mu )/k_{\text{B}}T)-1}}$$ Этот результат применим для каждого одночастичного уровня и, таким образом, формирует распределение Бозе-Эйнштейна для всего состояния системы.

Дисперсия , числа частиц ${\textstyle \sigma _{N}^{2}=\langle N^{2}\rangle -\langle N\rangle ^{2}}$, является: $$\sigma _{N}^{2}=k_{\text{B}}T\left({\frac {d\langle N\rangle }{d\mu }}\right)_{V,T}={\frac {\exp((\varepsilon -\mu )/k_{\text{B}}T)}{(\exp((\varepsilon -\mu )/k_{\text{B}}T)-1)^{2}}}=\langle N\rangle (1+\langle N\rangle ).$$

В результате для состояний с высокой занятостью стандартное отклонение числа частиц энергетического уровня очень велико, немного больше, чем само число частиц: $\sigma _{N}\approx \langle N\rangle$. Эта большая неопределенность связана с тем, что распределение вероятностей числа бозонов на данном энергетическом уровне представляет собой геометрическое распределение ; как это ни парадоксально, наиболее вероятное значение N всегда равно 0. (Напротив, классические частицы вместо этого имеют распределение Пуассона по числу частиц для данного состояния с гораздо меньшей неопределенностью ${\textstyle \sigma _{N,{\rm {classical}}}={\sqrt {\langle N\rangle }}}$, причем наиболее вероятное значение N находится вблизи $\langle N\rangle$.)

Вывод в каноническом подходе

Также возможно получить приближенную статистику Бозе-Эйнштейна в каноническом ансамбле . Эти выводы являются длинными и дают приведенные выше результаты только в асимптотическом пределе большого числа частиц. Причина в том, что общее число бозонов фиксировано в каноническом ансамбле. Распределение Бозе-Эйнштейна в этом случае может быть получено, как и в большинстве текстов, путем максимизации, но математически лучший вывод - это метод средних значений Дарвина-Фаулера , как подчеркивает Дингл. См. также Мюллер-Кирстен. Однако флуктуации основного состояния в конденсированной области заметно различаются в каноническом и великоканоническом ансамблях.

показывать

Вывод

Suppose we have a number of energy levels, labeled by index $i$, each level having energy $\varepsilon _{i}$ and containing a total of $n_{i}$ particles. Suppose each level contains $g_{i}$ distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy. The value of $g_{i}$ associated with level $i$ is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.

Let $w(n,g)$ be the number of ways of distributing $n$ particles among the $g$ sublevels of an energy level. There is only one way of distributing $n$ particles with one sublevel, therefore $w(n,1)=1$. It is easy to see that there are $(n+1)$ ways of distributing $n$ particles in two sublevels which we will write as: $$w(n,2)={\frac {(n+1)!}{n!1!}}.$$

With a little thought (see Notes below) it can be seen that the number of ways of distributing $n$ particles in three sublevels is $$w(n,3)=w(n,2)+w(n-1,2)+\cdots +w(1,2)+w(0,2)$$ so that $$w(n,3)=\sum _{k=0}^{n}w(n-k,2)=\sum _{k=0}^{n}{\frac {(n-k+1)!}{(n-k)!1!}}={\frac {(n+2)!}{n!2!}}$$ where we have used the following theorem involving binomial coefficients: $$\sum _{k=0}^{n}{\frac {(k+a)!}{k!a!}}={\frac {(n+a+1)!}{n!(a+1)!}}.$$

Continuing this process, we can see that $w(n,g)$ is just a binomial coefficient (See Notes below) $$w(n,g)={\frac {(n+g-1)!}{n!(g-1)!}}.$$

For example, the population numbers for two particles in three sublevels are 200, 110, 101, 020, 011, or 002 for a total of six which equals 4!/(2!2!). The number of ways that a set of occupation numbers $n_{i}$ can be realized is the product of the ways that each individual energy level can be populated: $$W=\prod _{i}w(n_{i},g_{i})=\prod _{i}{\frac {(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!}}\approx \prod _{i}{\frac {(n_{i}+g_{i})!}{n_{i}!(g_{i})!}}$$ where the approximation assumes that $n_{i}\gg 1$.

Following the same procedure used in deriving the Maxwell–Boltzmann statistics, we wish to find the set of $n_{i}$ for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of $W$ and $\ln(W)$ occur at the same value of $n_{i}$ and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers forming the function: $$f(n_{i})=\ln(W)+\alpha (N-\sum n_{i})+\beta (E-\sum n_{i}\varepsilon _{i})$$

Using the $n_{i}\gg 1$ approximation and using Stirling's approximation for the factorials $\left(x!\approx x^{x}\,e^{-x}\,{\sqrt {2\pi x}}\right)$ gives $$f(n_{i})=\sum _{i}(n_{i}+g_{i})\ln(n_{i}+g_{i})-n_{i}\ln(n_{i})+\alpha \left(N-\sum n_{i}\right)+\beta \left(E-\sum n_{i}\varepsilon _{i}\right)+K,$$ where K is the sum of a number of terms which are not functions of the $n_{i}$. Taking the derivative with respect to $n_{i}$, and setting the result to zero and solving for $n_{i}$, yields the Bose–Einstein population numbers: $$n_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}}-1}}.$$

By a process similar to that outlined in the Maxwell–Boltzmann statistics article, it can be seen that: $$d\ln W=\alpha \,dN+\beta \,dE$$ which, using Boltzmann's famous relationship $S=k_{\text{B}}\,\ln W$ becomes a statement of the second law of thermodynamics at constant volume, and it follows that $\beta ={\frac {1}{k_{\text{B}}T}}$ and $\alpha =-{\frac {\mu }{k_{\text{B}}T}}$ where S is the entropy, $\mu$ is the chemical potential, k_B is the Boltzmann constant and T is the temperature, so that finally: $$n_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}-1}}.$$

Note that the above formula is sometimes written: $$n_{i}={\frac {g_{i}}{e^{\varepsilon _{i}/k_{\text{B}}T}/z-1}},$$ where $z=\exp(\mu /k_{\text{B}}T)$ is the absolute activity, as noted by McQuarrie.

Also note that when the particle numbers are not conserved, removing the conservation of particle numbers constraint is equivalent to setting $\alpha$ and therefore the chemical potential $\mu$ to zero. This will be the case for photons and massive particles in mutual equilibrium and the resulting distribution will be the Planck distribution.

показывать

Примечания

A much simpler way to think of Bose–Einstein distribution function is to consider that n particles are denoted by identical balls and g shells are marked by g-1 line partitions. It is clear that the permutations of these n balls and g − 1 partitions will give different ways of arranging bosons in different energy levels. Say, for 3 (= n) particles and 3 (= g) shells, therefore (g − 1) = 2, the arrangement might be |●●|●, or ||●●●, or |●|●● , etc. Hence the number of distinct permutations of n + (g − 1) objects which have n identical items and (g − 1) identical items will be: $${\frac {(g-1+n)!}{(g-1)!n!}}$$

See the image for a visual representation of one such distribution of n particles in g boxes that can be represented as g − 1 partitions.

The image represents one possible distribution of bosonic particles in different boxes. The box partitions (green) can be moved around to change the size of the boxes and as a result of the number of bosons each box can contain.

OR

The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein distribution for beginners. The enumeration of cases (or ways) in the Bose–Einstein distribution can be recast as follows. Consider a game of dice throwing in which there are $n$ dice, with each die taking values in the set$\{1,\dots ,g\}$, for $g\geq 1$. The constraints of the game are that the value of a die $i$, denoted by $m_{i}$, has to be greater than or equal to the value of die $(i-1)$, denoted by $m_{i-1}$, in the previous throw, i.e., $m_{i}\geq m_{i-1}$. Thus a valid sequence of die throws can be described by an n-tuple $(m_{1},m_{2},\dots ,m_{n})$, such that $m_{i}\geq m_{i-1}$. Let $S(n,g)$ denote the set of these valid n-tuples:

$$S(n,g)=\left\{(m_{1},m_{2},\dots ,m_{n})\,{\Big |}\,m_{i}\geq m_{i-1},m_{i}\in \left\{1,\ldots ,g\right\},\forall i=1,\dots ,n\right\}.$$ (1)

Then the quantity $w(n,g)$ (defined above as the number of ways to distribute $n$ particles among the $g$ sublevels of an energy level) is the cardinality of $S(n,g)$, i.e., the number of elements (or valid n-tuples) in $S(n,g)$. Thus the problem of finding an expression for $w(n,g)$ becomes the problem of counting the elements in $S(n,g)$.

Example n = 4, g = 3: $$S(4,3)=\left\{\underbrace {(1111),(1112),(1113)} _{(a)},\underbrace {(1122),(1123),(1133)} _{(b)},\underbrace {(1222),(1223),(1233),(1333)} _{(c)},\underbrace {(2222),(2223),(2233),(2333),(3333)} _{(d)}\right\}$$ $$w(4,3)=15$$ (there are $15$ elements in $S(4,3)$)

Subset $(a)$ is obtained by fixing all indices $m_{i}$ to $1$, except for the last index, $m_{n}$, which is incremented from $1$ to $g=3$. Subset $(b)$ is obtained by fixing $m_{1}=m_{2}=1$, and incrementing $m_{3}$ from $2$ to $g=3$. Due to the constraint $m_{i}\geq m_{i-1}$ on the indices in $S(n,g)$, the index $m_{4}$ must automatically take values in $\left\{2,3\right\}$. The construction of subsets $(c)$ and $(d)$ follows in the same manner.

Each element of $S(4,3)$ can be thought of as a multiset of cardinality $n=4$; the elements of such multiset are taken from the set $\left\{1,2,3\right\}$ of cardinality $g=3$, and the number of such multisets is the multiset coefficient $$\left\langle {\begin{matrix}3\\4\end{matrix}}\right\rangle ={3+4-1 \choose 3-1}={3+4-1 \choose 4}={\frac {6!}{4!2!}}=15$$

More generally, each element of $S(n,g)$ is a multiset of cardinality $n$ (number of dice) with elements taken from the set $\left\{1,\dots ,g\right\}$ of cardinality $g$ (number of possible values of each die), and the number of such multisets, i.e., $w(n,g)$is the multiset coefficient

$$w(n,g)=\left\langle {\begin{matrix}g\\n\end{matrix}}\right\rangle ={g+n-1 \choose g-1}={g+n-1 \choose n}={\frac {(g+n-1)!}{n!(g-1)!}}$$

(2)

which is exactly the same as the formula for $w(n,g)$, as derived above with the aid of a theorem involving binomial coefficients, namely

$$\sum _{k=0}^{n}{\frac {(k+a)!}{k!a!}}={\frac {(n+a+1)!}{n!(a+1)!}}.$$

(3)

To understand the decomposition

$$w(n,g)=\sum _{k=0}^{n}w(n-k,g-1)=w(n,g-1)+w(n-1,g-1)+\dots +w(1,g-1)+w(0,g-1)$$

(4)

or for example, $n=4$ and $g=3$ $$w(4,3)=w(4,2)+w(3,2)+w(2,2)+w(1,2)+w(0,2),$$

let us rearrange the elements of $S(4,3)$ as follows $$S(4,3)=\left\{\underbrace {(1111),(1112),(1122),(1222),(2222)} _{(\alpha )},\underbrace {(111{\color {Red}{\underset {=}{3}}}),(112{\color {Red}{\underset {=}{3}}}),(122{\color {Red}{\underset {=}{3}}}),(222{\color {Red}{\underset {=}{3}}})} _{(\beta )},\underbrace {(11{\color {Red}{\underset {==}{33}}}),(12{\color {Red}{\underset {==}{33}}}),(22{\color {Red}{\underset {==}{33}}})} _{(\gamma )},\underbrace {(1{\color {Red}{\underset {===}{333}}}),(2{\color {Red}{\underset {===}{333}}})} _{(\delta )}\underbrace {({\color {Red}{\underset {====}{3333}}})} _{(\omega )}\right\}.$$

Clearly, the subset $(\alpha )$ of $S(4,3)$ is the same as the set $$S(4,2)=\left\{(1111),(1112),(1122),(1222),(2222)\right\}.$$

By deleting the index $m_{4}=3$ (shown in red with double underline) in the subset $(\beta )$ of $S(4,3)$, one obtains the set $$S(3,2)=\left\{(111),(112),(122),(222)\right\}.$$

In other words, there is a one-to-one correspondence between the subset $(\beta )$ of $S(4,3)$ and the set $S(3,2)$. We write $$(\beta )\longleftrightarrow S(3,2).$$

Similarly, it is easy to see that $$(\gamma )\longleftrightarrow S(2,2)=\left\{(11),(12),(22)\right\}$$ $$(\delta )\longleftrightarrow S(1,2)=\left\{(1),(2)\right\}$$ $$(\omega )\longleftrightarrow S(0,2)=\{\}=\varnothing .$$

Thus we can write $$S(4,3)=\bigcup _{k=0}^{4}S(4-k,2)$$ or more generally,

$$S(n,g)=\bigcup _{k=0}^{n}S(n-k,g-1);$$

(5)

and since the sets $$S(i,g-1),{\text{ for }}i=0,\dots ,n$$ are non-intersecting, we thus have

$$w(n,g)=\sum _{k=0}^{n}w(n-k,g-1),$$

(6)

with the convention that

$$w(0,g)=1\ ,\forall g,{\text{ and }}w(n,0)=1\ ,\forall n.$$

(7)

Continuing the process, we arrive at the following formula $$w(n,g)=\sum _{k_{1}=0}^{n}\sum _{k_{2}=0}^{n-k_{1}}w(n-k_{1}-k_{2},g-2)=\sum _{k_{1}=0}^{n}\sum _{k_{2}=0}^{n-k_{1}}\cdots \sum _{k_{g}=0}^{n-\sum _{j=1}^{g-1}k_{j}}w(n-\sum _{i=1}^{g}k_{i},0).$$ Using the convention (7)₂ above, we obtain the formula

$$w(n,g)=\sum _{k_{1}=0}^{n}\sum _{k_{2}=0}^{n-k_{1}}\cdots \sum _{k_{g}=0}^{n-\sum _{j=1}^{g-1}k_{j}}1,$$

(8)

keeping in mind that for $q$ and $p$ being constants, we have

$$\sum _{k=0}^{q}p=qp.$$ (9)

It can then be verified that (8) and (2) give the same result for $w(4,3)$, $w(3,3)$, $w(3,2)$, etc.

Междисциплинарные приложения

Основная статья: Конденсация Бозе – Эйнштейна (теория сетей)

Распределение Бозе-Эйнштейна, рассматриваемое как чистое распределение вероятностей , нашло применение в других областях:

• В последние годы статистика Бозе-Эйнштейна также использовалась как метод взвешивания терминов при поиске информации . Этот метод входит в коллекцию моделей DFR («Расхождение от случайности»). Основная идея заключается в том, что статистика Бозе-Эйнштейна может быть полезным индикатором в тех случаях, когда конкретный термин и конкретный документ имеют значительную взаимосвязь, которая не возникла бы чисто случайно. Исходный код для реализации этой модели доступен в проекте Terrier в Университете Глазго.
• Эволюция многих сложных систем, включая Всемирную паутину , бизнес и сети цитирования, закодирована в динамической сети, описывающей взаимодействия между составляющими системы. Несмотря на свою необратимую и неравновесную природу, эти сети следуют статистике Бозе и могут подвергаться конденсации Бозе-Эйнштейна. Обращение к динамическим свойствам этих неравновесных систем в рамках равновесных квантовых газов предсказывает, что явления «преимущество первопроходца», «пригодный-богатый» (FGR) и «победитель получает все», наблюдаемые в конкурентных системах, термодинамически различные фазы лежащих в основе развивающихся сетей.

См. также

• Корреляции Бозе-Эйнштейна
• Конденсат Бозе – Эйнштейна
• Бозе-газ
• Эйнштейн твердый
• Бозон Хиггса
• Парастатистика
• Закон Планка об излучении черного тела
• Сверхпроводимость
• Статистика Ферми – Дирака
• Статистика Максвелла – Больцмана

Ссылки

• Аннетт, Джеймс Ф. (2004). Сверхпроводимость, сверхтекучести и конденсаты . Нью-Йорк: Издательство Оксфордского университета. ISBN  0-19-850755-0 .
• Картер, Эшли Х. (2001). Классическая и статистическая термодинамика . Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл. ISBN  0-13-779208-5 .
• Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Река Аппер-Сэддл, Нью-Джерси: Пирсон, Прентис-Холл. ISBN  0-13-191175-9 .
• МакКуорри, Дональд А. (2000). Статистическая механика (1-е изд.). Саусалито, Калифорния: Университетские научные книги. п. 55 . ISBN  1-891389-15-7 .