Центростремительная сила

Не путать с Центробежной силой . Чтобы узнать о других значениях слова «центростремительный», см. Центростремительный (значения) .

Частица нарушается ее равномерное линейное движение серией коротких толчков (1, 2,...), придающих ее траектории почти круговую форму. Сила называется центростремительной силой в пределе непрерывно действующей силы, направленной к центру кривизны пути.

Центростремительная сила (от лат. centrum — «центр» и petere — «искать»). ) — это сила , которая заставляет тело двигаться по криволинейной траектории . Направление центростремительной силы всегда ортогонально движению тела и к неподвижной точке мгновенного центра кривизны траектории. Исаак Ньютон описал это как «силу, с помощью которой тела притягиваются, толкаются или каким-либо образом стремятся к точке, как к центру». В механике Ньютона гравитация обеспечивает центростремительную силу, вызывающую астрономические орбиты .

Одним из распространенных примеров центростремительной силы является случай, когда тело движется с равномерной скоростью по круговой траектории. Центростремительная сила направлена ​​под прямым углом к ​​движению, а также по радиусу к центру круговой траектории. Математическое описание было получено в 1659 году голландским физиком Христианом Гюйгенсом .

Формула

Из кинематики криволинейного движения известно, что тело, движущееся с тангенциальной скоростью v по траектории радиуса кривизны r, ускоряется к центру кривизны со скоростью $${\textbf {a}}_{c}=\lim _{\Delta t\to 0}{\frac {\Delta {\textbf {v}}}{\Delta t}},\quad a_{c}={\frac {v^{2}}{r}}$$Здесь, $a_{c}$ центростремительное ускорение и $\Delta {\textbf {v}}$ – разность векторов скорости при $t+\Delta {t}$ и $t$.

Согласно второму закону Ньютона , причиной ускорения является результирующая сила, действующая на объект, которая пропорциональна его массе m и его ускорению. Сила, обычно называемая центростремительной силой , имеет величину $$F_{c}=ma_{c}=m{\frac {v^{2}}{r}}$$и, как и центростремительное ускорение, направлено к центру кривизны траектории объекта.

Вывод

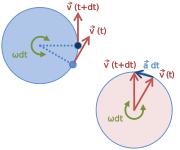
Центростремительное ускорение можно вывести из диаграммы векторов скорости в двух случаях. При равномерном круговом движении скорости имеют постоянную величину. Поскольку каждый из них перпендикулярен соответствующему вектору положения, простое вычитание вектора подразумевает два подобных равнобедренных треугольника с равными углами, один из которых основание содержит $\Delta {\textbf {v}}$ и ноги длина $v$, а другой база - $\Delta {\textbf {r}}$ ( разница векторов положения ) и участка длина $r$: $${\frac {|\Delta {\textbf {v}}|}{v}}={\frac {|\Delta {\textbf {r}}|}{r}}$$$$|\Delta {\textbf {v}}|={\frac {v}{r}}|\Delta {\textbf {r}}|$$Поэтому, $|\Delta {\textbf {v}}|$ можно заменить на ${\frac {v}{r}}|\Delta {\textbf {r}}|$: $$a_{c}=\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta t}}={\frac {v}{r}}\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=\omega \lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=v\omega ={\frac {v^{2}}{r}}$$Направление силы — к центру круга, по которому движется объект, или к соприкасающемуся кругу (круг, который лучше всего соответствует локальному пути объекта, если путь не круговой). Скорость в формуле возведена в квадрат, поэтому удвоенная скорость требует вчетверо большей силы при заданном радиусе.

Эту силу также иногда записывают через угловую скорость ω объекта относительно центра окружности, связанную с тангенциальной скоростью по формуле $$v=\omega r$$так что $$F_{c}=mr\omega ^{2}\,.$$

Выражается с использованием орбитального периода T за один оборот круга: $$\omega ={\frac {2\pi }{T}}$$уравнение становится $$F_{c}=mr\left({\frac {2\pi }{T}}\right)^{2}.$$

В ускорителях частиц скорость может быть очень высокой (близкой к скорости света в вакууме), поэтому та же самая масса покоя теперь обладает большей инерцией (релятивистская масса), тем самым требуя большей силы для того же центростремительного ускорения, поэтому уравнение принимает вид: $$F_{c}={\frac {\gamma mv^{2}}{r}}$$где $$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$$является фактором Лоренца .

Таким образом, центростремительная сила определяется выражением: $$F_{c}=\gamma mv\omega$$что представляет собой скорость изменения релятивистского импульса $\gamma mv$.

Источники

Телу, испытывающему равномерное круговое движение, требуется центростремительная сила, направленная к оси, как показано, для поддержания его кругового движения.

В случае объекта, который раскачивается на конце веревки в горизонтальной плоскости, центростремительная сила, действующая на объект, создается за счет натяжения веревки. Пример с веревкой — это пример, включающий силу «тяги». Центростремительная сила также может быть представлена ​​как «толкающая» сила, например, в случае, когда нормальная реакция стены создает центростремительную силу для стены смерти или наездника Ротора .

Идея Ньютона о центростремительной силе соответствует тому, что сегодня называют центральной силой . Когда спутник находится на орбите вокруг планеты , гравитация считается центростремительной силой, хотя в случае эксцентрических орбит гравитационная сила направлена ​​к фокусу, а не к мгновенному центру кривизны.

Другой пример центростремительной силы возникает в спирали, прослеживающейся при движении заряженной частицы в однородном магнитном поле в отсутствие других внешних сил. В этом случае магнитная сила — это центростремительная сила, действующая в направлении оси спирали.

Анализ нескольких случаев

Ниже приведены три примера возрастающей сложности с выводом формул, определяющих скорость и ускорение.

Равномерное круговое движение

См. Также: Равномерное круговое движение.

Равномерное круговое движение относится к случаю постоянной скорости вращения. Вот два подхода к описанию этого случая.

Вывод исчисления

В двух измерениях вектор положения ${\textbf {r}}$, который имеет величину (длину) $r$ и направлен под углом $\theta$ над осью x, может быть выражено в декартовых координатах с использованием единичных векторов ${\hat {\mathbf {x} }}$ и ${\hat {\mathbf {y} }}$: $${\textbf {r}}=r\cos(\theta ){\hat {\mathbf {x} }}+r\sin(\theta ){\hat {\mathbf {y} }}.$$

Предположение о равномерном круговом движении требует трех вещей:

1. Объект движется только по кругу.
2. Радиус круга $r$ не меняется во времени.
3. Объект движется с постоянной угловой скоростью $\omega$ по кругу. Поэтому, $\theta =\omega t$ где $t$ это время.

Скорость ​ ${\textbf {v}}$ и ускорение ${\textbf {a}}$ движения являются первой и второй производными положения по времени:

$${\textbf {r}}=r\cos(\omega t){\hat {\mathbf {x} }}+r\sin(\omega t){\hat {\mathbf {y} }},$$$${\textbf {v}}={\dot {\textbf {r}}}=-r\omega \sin(\omega t){\hat {\mathbf {x} }}+r\omega \cos(\omega t){\hat {\mathbf {y} }},$$$${\textbf {a}}={\ddot {\textbf {r}}}=-\omega ^{2}(r\cos(\omega t){\hat {\mathbf {x} }}+r\sin(\omega t){\hat {\mathbf {y} }}).$$

Термин в скобках является оригинальным выражением ${\textbf {r}}$ в декартовых координатах . Следовательно, $${\textbf {a}}=-\omega ^{2}{\textbf {r}}.$$отрицательное показывает, что ускорение направлено к центру круга (противоположно радиусу), поэтому оно называется «центростремительным» (т.е. «стремящимся к центру»). Хотя объекты естественным образом следуют по прямой траектории (из-за инерции ), это центростремительное ускорение описывает траекторию кругового движения, вызванную центростремительной силой.

Вывод с использованием векторов

Векторные соотношения для равномерного кругового движения; вектор Ω, представляющий вращение, нормален к плоскости орбиты с полярностью, определяемой правилом правой руки , и величиной dθ / dt .

Изображение справа показывает векторные соотношения для равномерного кругового движения. Само вращение представлено вектором угловой скорости Ω , который нормален к плоскости орбиты (с использованием правила правой руки ) и имеет величину, определяемую выражением:

$|\mathbf {\Omega } |={\frac {\mathrm {d} \theta }{\mathrm {d} t}}=\omega \ ,$

где θ - угловое положение в момент времени t . В этом подразделе d θ /d t предполагается постоянным, не зависящим от времени. Расстояние dℓ, пройденное частицей за время d t по круговой траектории, равно

$\mathrm {d} {\boldsymbol {\ell }}=\mathbf {\Omega } \times \mathbf {r} (t)\mathrm {d} t\ ,$

который по свойствам векторного векторного произведения имеет величину r d θ и находится в направлении, касательно траектории окружности.

Следовательно,

${\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\lim _{{\Delta }t\to 0}{\frac {\mathbf {r} (t+{\Delta }t)-\mathbf {r} (t)}{{\Delta }t}}={\frac {\mathrm {d} {\boldsymbol {\ell }}}{\mathrm {d} t}}\ .$

Другими словами,

$\mathbf {v} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {\boldsymbol {\ell }} }{\mathrm {d} t}}=\mathbf {\Omega } \times \mathbf {r} (t)\ .$

Дифференцируя по времени, $$\mathbf {a} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {v} }{d\mathrm {t} }}=\mathbf {\Omega } \times {\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}=\mathbf {\Omega } \times \left[\mathbf {\Omega } \times \mathbf {r} (t)\right]\ .$$

Формула Лагранжа гласит: $$\mathbf {a} \times \left(\mathbf {b} \times \mathbf {c} \right)=\mathbf {b} \left(\mathbf {a} \cdot \mathbf {c} \right)-\mathbf {c} \left(\mathbf {a} \cdot \mathbf {b} \right)\ .$$

Применяя формулу Лагранжа с учетом того, что Ω • r ( t ) = 0 всегда, $$\mathbf {a} =-{|\mathbf {\Omega |} }^{2}\mathbf {r} (t)\ .$$

Другими словами, ускорение направлено прямо противоположно радиальному смещению r всегда и имеет величину: $$|\mathbf {a} |=|\mathbf {r} (t)|\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}=r{\omega }^{2}$$где вертикальные полосы |...| обозначают величину вектора, которая в случае r ( t ) является просто радиусом r пути. Этот результат согласуется с предыдущим разделом, хотя обозначения немного другие.

Когда скорость вращения делается постоянной при анализе неравномерного кругового движения , этот анализ согласуется с этим.

Достоинство векторного подхода состоит в том, что он явно не зависит от какой-либо системы координат.

Пример: поворот с креном

Основная статья: Поворот с накренением

Смотрите также: Реактивная центробежная сила

Верхняя панель: мяч на круговой дорожке с наклоном, движущийся с постоянной скоростью v ; Нижняя панель: Силы, действующие на шар.

На верхней панели изображения справа показан мяч, движущийся по кругу по наклонной кривой. Кривая наклонена под углом θ к горизонту, и поверхность дороги считается скользкой. Цель состоит в том, чтобы найти, под каким углом должен быть крен, чтобы мяч не соскользнул с дороги. Интуиция подсказывает нам, что на ровном повороте без крена мяч просто соскользнет с дороги; в то время как при очень крутом вираже мяч будет скользить к центру, если он не пройдет по кривой быстро.

Помимо любого ускорения, которое может возникнуть в направлении траектории, нижняя панель изображения выше показывает силы, действующие на шар. Есть две силы; один — сила тяжести, направленная вертикально вниз через центр масс шара m g , где m — масса шара, а g — ускорение свободного падения ; вторая — это направленная вверх нормальная сила, действующая со стороны дороги под прямым углом покрытию ​​дорожному _к . Центростремительная сила, необходимая для криволинейного движения, также показана выше. Эта центростремительная сила не является третьей силой, приложенной к мячу, а скорее должна обеспечиваться чистой силой, действующей на шар, возникающей в результате векторного сложения нормальной силы и силы тяжести . Результирующая или чистая сила, действующая на шар, найденная векторным сложением нормальной силы, действующей на дорогу, и вертикальной силы, вызванной гравитацией, должна равняться центростремительной силе, обусловленной необходимостью двигаться по круговой траектории. Криволинейное движение сохраняется до тех пор, пока эта результирующая сила обеспечивает центростремительную силу, необходимую для движения.

Горизонтальная чистая сила, действующая на шар, представляет собой горизонтальную составляющую силы со стороны дороги, имеющую величину | Ф _ч | = м | п _| ​грех θ . Вертикальная составляющая силы со стороны дороги должна противодействовать силе гравитации: | Ф _в | = м | п _| ​потому что θ знак равно м | г | , что подразумевает | п _| ​= | г | / потому что θ . Подставив в приведенную выше формулу | Ф _ч | дает горизонтальную силу: $$|\mathbf {F} _{\mathrm {h} }|=m|\mathbf {g} |{\frac {\sin \theta }{\cos \theta }}=m|\mathbf {g} |\tan \theta \,.$$

С другой стороны, при скорости | в | на круговой траектории радиуса r кинематика говорит, что сила, необходимая для непрерывного поворота шара в поворот, представляет собой радиально направленную внутрь центростремительную силу F _c величины: $$|\mathbf {F} _{\mathrm {c} }|=m|\mathbf {a} _{\mathrm {c} }|={\frac {m|\mathbf {v} |^{2}}{r}}\,.$$

Следовательно, мяч находится на устойчивой траектории, когда угол дороги задан так, чтобы удовлетворять условию: $$m|\mathbf {g} |\tan \theta ={\frac {m|\mathbf {v} |^{2}}{r}}\,,$$или, $$\tan \theta ={\frac {|\mathbf {v} |^{2}}{|\mathbf {g} |r}}\,.$$

Когда угол крена θ приближается к 90°, функция тангенса приближается к бесконечности, что позволяет использовать более высокие значения | в | ² / р . Другими словами, это уравнение утверждает, что для больших скоростей (больших | v |) дорога должна иметь более крутой крен (большее значение для θ ), а для более крутых поворотов (меньшее r ) дорога также должна иметь более крутой крен, что соответствует с интуицией. Когда угол θ не удовлетворяет вышеуказанному условию, горизонтальная составляющая силы, действующей на дорогу, не обеспечивает правильную центростремительную силу, и для обеспечения разницы требуется дополнительная сила трения, касательная к поверхности дороги. Если трение не может этого сделать (т. е. коэффициент трения превышен), шарик соскальзывает на другой радиус, где может быть реализован баланс.

Эти идеи применимы и к воздушным полетам. См. руководство пилота ФАУ.

Неравномерное круговое движение

См. Также: Круговое движение и Неравномерное круговое движение.

/ Р .

В качестве обобщения случая равномерного кругового движения предположим, что угловая скорость вращения не является постоянной. Ускорение теперь имеет тангенциальную составляющую, как показано на изображении справа. Этот случай используется для демонстрации стратегии вывода, основанной на полярной системе координат .

Пусть r ( t ) — вектор, который описывает положение точечной массы как функцию времени. Поскольку мы предполагаем круговое движение , пусть ( t ) = R · ur _r , где R — константа (радиус круга), а ur _{указывающий} — единичный вектор, от начала координат к точечной массе. Направление u _r описывается θ , углом между осью x и единичным вектором, измеренным против часовой стрелки от оси x. Другой единичный вектор полярных координат u _θ перпендикулярен ur _и указывает в направлении увеличения θ . Эти полярные единичные векторы могут быть выражены через декартовы единичные векторы в направлениях x и y , обозначенные ${\hat {\mathbf {i} }}$ и ${\hat {\mathbf {j} }}$ соответственно: $$\mathbf {u} _{r}=\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}$$ и $$\mathbf {u} _{\theta }=-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}.$$

Чтобы найти скорость, можно дифференцировать: $${\begin{aligned}\mathbf {v} &=r{\frac {d\mathbf {u} _{r}}{dt}}\\&=r{\frac {d}{dt}}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}{\frac {d}{d\theta }}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\left(-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\mathbf {u} _{\theta }\\&=\omega r\mathbf {u} _{\theta }\end{aligned}}$$где ω — угловая скорость dθ / dt .

Этот результат для скорости соответствует ожиданиям, что скорость должна быть направлена ​​по касательной к окружности и что величина скорости должна быть rω . Еще раз дифференцируя и отмечая, что $${\frac {d\mathbf {u} _{\theta }}{dt}}=-{\frac {d\theta }{dt}}\mathbf {u} _{r}=-\omega \mathbf {u} _{r}\ ,$$мы находим, что ускорение a равно: $$\mathbf {a} =r\left({\frac {d\omega }{dt}}\mathbf {u} _{\theta }-\omega ^{2}\mathbf {u} _{r}\right)\ .$$

Таким образом, радиальная и тангенциальная составляющие ускорения равны: $$\mathbf {a} _{r}=-\omega ^{2}r\ \mathbf {u} _{r}=-{\frac {|\mathbf {v} |^{2}}{r}}\ \mathbf {u} _{r}$$ и $$\mathbf {a} _{\theta }=r\ {\frac {d\omega }{dt}}\ \mathbf {u} _{\theta }={\frac {d|\mathbf {v} |}{dt}}\ \mathbf {u} _{\theta }\ ,$$где | в | = r ω – величина скорости (скорости).

Эти уравнения математически выражают то, что в случае объекта, который движется по круговой траектории с изменяющейся скоростью, ускорение тела можно разложить на перпендикулярную составляющую , изменяющую направление движения (центростремительное ускорение), и параллельную составляющую. , или тангенциальная составляющая , изменяющая скорость.

Общее плоское движение

См. также: Обобщенные силы , Обобщенная сила , Криволинейные координаты , Обобщенные координаты и Ортогональные координаты.

Вектор положения r всегда указывает радиально от начала координат.

Вектор скорости v , всегда касательный к траектории движения.

Вектор ускорения a не параллелен радиальному движению, а смещен угловым ускорением и ускорением Кориолиса, не касается траектории, а смещен центростремительным и радиальным ускорениями.

Кинематические векторы в плоских полярных координатах. Обратите внимание, что установка не ограничивается двухмерным пространством, а плоскостью в любом более высоком измерении.

Полярные единичные векторы в два момента времени t и t + dt для частицы с траекторией r ( t ); слева единичные векторы u _ρ и u _θ в два момента времени перемещаются так, что все их хвосты встречаются, и показано, что они очерчивают дугу окружности единичного радиуса. Их поворот во времени dt равен d θ, на тот же угол, что и поворот траектории r ( t ).

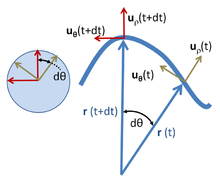
Полярные координаты

Приведенные выше результаты можно, возможно, получить проще в полярных координатах и ​​в то же время распространить на общее движение внутри плоскости, как показано ниже. В полярных координатах на плоскости используются радиальный единичный вектор u _ρ и угловой единичный вектор u _θ , как показано выше. Частица в позиции r описывается следующим образом:

$$\mathbf {r} =\rho \mathbf {u} _{\rho }\ ,$$

где обозначение ρ используется для описания расстояния пути от начала координат вместо R, чтобы подчеркнуть, что это расстояние не фиксировано, а меняется со временем. Единичный вектор u _ρ движется вместе с частицей и всегда указывает в том же направлении, что и r ( t ). Единичный вектор u _θ также перемещается вместе с частицей и остается ортогональным u _ρ . Таким образом, u _ρ и u _θ образуют локальную декартову систему координат, прикрепленную к частице и привязанную к пути, пройденному частицей. Перемещая единичные векторы так, чтобы их хвосты совпадали, как видно из круга слева на изображении выше, видно, что u _ρ и u _θ образуют прямоугольную пару с кончиками единичного круга, которые движутся взад и вперед по периметр этого круга с тем же углом θ ( t ), что и r ( t ).

Когда частица движется, ее скорость равна

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}\,.$

производная единичного вектора u _ρ Для оценки скорости необходима . Поскольку u _ρ является единичным вектором, его величина фиксирована и может изменяться только по направлению, то есть его изменение d u _ρ имеет компоненту, только перпендикулярную u _ρ . Когда траектория r ( t ) поворачивается на величину dθ , uρ , _{которая} указывает в том же направлении, что и r ( t ), также поворачивается на dθ . См. изображение выше. Следовательно, изменение u _ρ равно

$\mathrm {d} \mathbf {u} _{\rho }=\mathbf {u} _{\theta }\mathrm {d} \theta \,,$

или

${\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}=\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\,.$

скорость изменения u _θ Аналогичным образом находится . Как и u _ρ , u _θ является единичным вектором и может только вращаться без изменения размера. Чтобы оставаться ортогональным к u _ρ, пока траектория r ( t ) поворачивается на величину d θ , u _θ , ортогональный r ( t ), также поворачивается на d θ . См. изображение выше. Следовательно, изменение d u _θ ортогонально u _θ и пропорционально d θ (см. изображение выше):

${\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\rho }\,.$

В приведенном выше уравнении знак отрицательный: для сохранения ортогональности, если d u _ρ положительное с d θ , то d u _θ должно уменьшаться.

Подставляя производную u _ρ в выражение для скорости:

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}=v_{\rho }\mathbf {u} _{\rho }+v_{\theta }\mathbf {u} _{\theta }=\mathbf {v} _{\rho }+\mathbf {v} _{\theta }\,.$

Для получения ускорения делается еще одно дифференцирование по времени:

$\mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\,.$

Подставив производные u _ρ и u _θ , ускорение частицы составит:

${\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} v_{\rho }}{\mathrm {d} t}}-{\frac {v_{\theta }^{2}}{\rho }}\right]+\mathbf {u} _{\theta }\left[{\frac {2}{\rho }}v_{\rho }v_{\theta }+\rho {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {v_{\theta }}{\rho }}\right]\,.\end{aligned}}$

В качестве частного примера, если частица движется по кругу постоянного радиуса R , то d ρ /d t = 0, v = v _θ и:

$$\mathbf {a} =\mathbf {u} _{\rho }\left[-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]=\mathbf {u} _{\rho }\left[-{\frac {v^{2}}{r}}\right]+\mathbf {u} _{\theta }\left[{\frac {\mathrm {d} v}{\mathrm {d} t}}\right]\$$

где $v=v_{\theta }.$

Эти результаты согласуются с результатами, полученными выше для неравномерного кругового движения . См. также статью о неравномерном круговом движении . Если это ускорение умножить на массу частицы, главным членом будет центростремительная сила, а отрицательное значение второго члена, связанное с угловым ускорением, иногда называют силой Эйлера .

Для траекторий, отличных от кругового движения, например, более общей траектории, представленной на изображении выше, мгновенный центр вращения и радиус кривизны траектории связаны лишь косвенно с системой координат, определяемой u _ρ и u _θ, и с длина | р ( т )| = р . Следовательно, в общем случае выделить центростремительные и эйлеровы члены из приведенного выше общего уравнения ускорения непросто. Для непосредственного решения этой проблемы предпочтительнее использовать местные координаты, как обсуждается далее.

Местные координаты

Локальная система координат для плоского движения по кривой. показаны два разных положения для расстояний s и s + ds На кривой . В каждой позиции s единичный вектор un _{указывает} вдоль внешней нормали к кривой, а единичный вектор u _t касается пути. Радиус кривизны траектории равен ρ, который определяется по скорости вращения касательной к кривой относительно длины дуги, и представляет собой радиус соприкасающейся окружности в положении s . Единичный круг слева показывает вращение единичных векторов с помощью s .

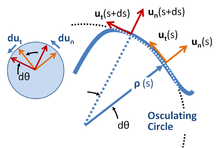
Локальные координаты означают набор координат, которые перемещаются вместе с частицей. и имеют ориентацию, определяемую траекторией частицы. Единичные векторы формируются, как показано на изображении справа, как по касательной, так и по нормали к пути. Эту систему координат иногда называют внутренними координатами или координатами пути. или nt-coordinates для нормально-тангенциальных , относящихся к этим единичным векторам. Эти координаты представляют собой особый пример более общего понятия локальных координат из теории дифференциальных форм.

Расстояние по пути частицы — это длина дуги s , считающаяся известной функцией времени.

$s=s(t)\ .$

Центр кривизны определяется в каждой позиции s, расстоянии ρ ( радиус кривизны ) от кривой на линии по нормали un _{расположенной на} ( s ). Требуемое расстояние ρ ( s ) при длине дуги s определяется через скорость вращения касательной к кривой, которая, в свою очередь, определяется самим путем. Если ориентация касательной относительно некоторого начального положения равна θ ( s ), то ρ ( s ) определяется производной dθ / ds :

${\frac {1}{\rho (s)}}=\kappa (s)={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$

Радиус кривизны обычно принимают положительным (т. е. абсолютной величиной), а кривизну κ — величиной со знаком.

Геометрический подход к нахождению центра кривизны и радиуса кривизны использует предельный процесс, ведущий к соприкасающемуся кругу . См. изображение выше.

Используя эти координаты, движение по траектории рассматривается как последовательность круговых траекторий с постоянно меняющимся центром, и в каждой позиции s представляет собой неравномерное круговое движение в этой позиции с радиусом ρ . Тогда локальное значение угловой скорости вращения определяется выражением:

$\omega (s)={\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}{\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {1}{\rho (s)}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {v(s)}{\rho (s)}}\ ,$

с местной скоростью v, определяемой по формуле:

$v(s)={\frac {\mathrm {d} s}{\mathrm {d} t}}\ .$

Что касается других примеров выше, поскольку единичные векторы не могут изменить величину, скорость их изменения всегда перпендикулярна их направлению (см. левую вставку на изображении выше):

${\frac {d\mathbf {u} _{\mathrm {n} }(s)}{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {d\theta }{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {1}{\rho }}\ ;$ ${\frac {d\mathbf {u} _{\mathrm {t} }(s)}{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} \theta }{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {1}{\rho }}\ .$

Следовательно, скорость и ускорение равны:

$\mathbf {v} (t)=v\mathbf {u} _{\mathrm {t} }(s)\ ;$

и используя цепное правило дифференцирования :

$\mathbf {a} (t)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ;$ с тангенциальным ускорением ${\frac {\mathrm {\mathrm {d} } v}{\mathrm {\mathrm {d} } t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ v\ .$

В этой локальной системе координат ускорение напоминает выражение для неравномерного кругового движения с локальным радиусом ρ ( s ), а центростремительное ускорение идентифицируется как второй член.

Распространение этого подхода на трехмерные пространственные кривые приводит к формулам Френе – Серре .

Альтернативный подход

Глядя на изображение выше, можно задаться вопросом, была ли адекватно учтена разница в кривизне между ρ ( s ) и ρ ( s + d s ) при вычислении длины дуги как d s = ρ ( s )d θ . Уверенность в этом вопросе можно найти, используя более формальный подход, изложенный ниже. Этот подход также имеет связь со статьей о кривизне .

Чтобы ввести единичные векторы локальной системы координат, один из подходов состоит в том, чтобы начать с декартовых координат и описать локальные координаты в терминах этих декартовых координат. С точки зрения длины дуги s пусть путь описывается как: $$\mathbf {r} (s)=\left[x(s),\ y(s)\right].$$

Тогда постепенное смещение по пути d s описывается формулой: $$\mathrm {d} \mathbf {r} (s)=\left[\mathrm {d} x(s),\ \mathrm {d} y(s)\right]=\left[x'(s),\ y'(s)\right]\mathrm {d} s\ ,$$

где штрихи введены для обозначения производных по s . Величина этого смещения равна d s , что показывает, что:

$\left[x'(s)^{2}+y'(s)^{2}\right]=1\ .$ (уравнение 1)

Это смещение обязательно является касательной к кривой в точке s , показывая, что касательный единичный вектор к кривой равен: $$\mathbf {u} _{\mathrm {t} }(s)=\left[x'(s),\ y'(s)\right],$$а внешний единичный вектор, нормаль к кривой, равен $$\mathbf {u} _{\mathrm {n} }(s)=\left[y'(s),\ -x'(s)\right],$$

Ортогональность можно проверить, показав, что скалярное произведение вектора равно нулю. Единичная величина этих векторов является следствием уравнения. 1 . Используя касательный вектор, угол θ касательной к кривой определяется как: $$\sin \theta ={\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=y'(s)\ ;$$ и $\cos \theta ={\frac {x'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=x'(s)\ .$

Радиус кривизны вводится совершенно формально (без необходимости геометрической интерпретации) как: $${\frac {1}{\rho }}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$$

Производную θ можно найти из производной для sin θ : $${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}=\cos \theta {\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}\cos \theta \ ={\frac {1}{\rho }}x'(s)\ .$$

Сейчас: $${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}={\frac {\mathrm {d} }{\mathrm {d} s}}{\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}={\frac {y''(s)x'(s)^{2}-y'(s)x'(s)x''(s)}{\left(x'(s)^{2}+y'(s)^{2}\right)^{3/2}}}\ ,$$в котором знаменатель равен единице. Используя эту формулу для производной синуса, радиус кривизны становится: $${\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}=y''(s)x'(s)-y'(s)x''(s)={\frac {y''(s)}{x'(s)}}=-{\frac {x''(s)}{y'(s)}}\ ,$$где эквивалентность форм вытекает из дифференцирования уравнения (1). 1 : $$x'(s)x''(s)+y'(s)y''(s)=0\ .$$По этим результатам можно найти ускорение: $${\begin{aligned}\mathbf {a} (s)&={\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {v} (s)={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\end{aligned}}$$ взяв скалярное произведение с единичными векторами u _t ( s ) и un _{в чем можно убедиться ,} ( s ). Этот результат для ускорения такой же, как и для кругового движения, основанного на радиусе ρ . Используя эту систему координат в инерциальной системе отсчета, легко определить силу, нормальную к траектории, как центростремительную силу, а силу, параллельную траектории, как тангенциальную силу. С качественной точки зрения путь можно аппроксимировать дугой окружности в течение ограниченного времени, а в течение ограниченного времени применяется определенный радиус кривизны, центробежные силы и силы Эйлера можно анализировать на основе кругового движения с этим радиусом. .

Этот результат для ускорения согласуется с полученным ранее. Однако в этом подходе вопрос изменения радиуса кривизны с изменением s решается совершенно формально, в соответствии с геометрической интерпретацией, но не полагаясь на нее, тем самым избегая любых вопросов, которые может возникнуть на изображении выше, о пренебрежении изменением ρ .

Пример: круговое движение

Чтобы проиллюстрировать приведенные выше формулы, пусть x , y задаются как:

$x=\alpha \cos {\frac {s}{\alpha }}\ ;\ y=\alpha \sin {\frac {s}{\alpha }}\ .$

Затем:

$x^{2}+y^{2}=\alpha ^{2}\ ,$

который можно представить как круговой путь вокруг начала координат с радиусом α . Положение s = 0 соответствует [ α , 0] или 3 часам. Для использования приведенного выше формализма необходимы производные:

$y^{\prime }(s)=\cos {\frac {s}{\alpha }}\ ;\ x^{\prime }(s)=-\sin {\frac {s}{\alpha }}\ ,$

$y^{\prime \prime }(s)=-{\frac {1}{\alpha }}\sin {\frac {s}{\alpha }}\ ;\ x^{\prime \prime }(s)=-{\frac {1}{\alpha }}\cos {\frac {s}{\alpha }}\ .$

Имея эти результаты, можно убедиться в том, что:

$x^{\prime }(s)^{2}+y^{\prime }(s)^{2}=1\ ;\ {\frac {1}{\rho }}=y^{\prime \prime }(s)x^{\prime }(s)-y^{\prime }(s)x^{\prime \prime }(s)={\frac {1}{\alpha }}\ .$

Также можно найти единичные векторы:

$\mathbf {u} _{\mathrm {t} }(s)=\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]\ ;\ \mathbf {u} _{\mathrm {n} }(s)=\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]\ ,$

которые служат для того, чтобы показать, что s = 0 находится в позиции [ ρ , 0] и s = ρ π/2 в [0, ρ ], что согласуется с исходными выражениями для x и y . Другими словами, s измеряется против часовой стрелки по кругу от 3 часов. Также можно найти производные этих векторов:

${\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {t} }(s)=-{\frac {1}{\alpha }}\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]=-{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ;$

$\ {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {n} }(s)={\frac {1}{\alpha }}\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]={\frac {1}{\alpha }}\mathbf {u} _{\mathrm {t} }(s)\ .$

зависимость s Чтобы получить скорость и ускорение, необходима от времени. Для движения против часовой стрелки с переменной скоростью v ( t ):

$s(t)=\int _{0}^{t}\ dt^{\prime }\ v(t^{\prime })\ ,$

где v ( t ) — скорость, t — время и s ( t = 0) = 0. Тогда:

$\mathbf {v} =v(t)\mathbf {u} _{\mathrm {t} }(s)\ ,$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)+v{\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-v{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} s}{\mathrm {d} t}}$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ,$

где уже установлено, что α = ρ. Это ускорение является стандартным результатом неравномерного кругового движения .

См. также

• Аналитическая механика
• Прикладная механика
• Теорема Бертрана
• Центральная сила
• Центробежная сила
• Круговое движение
• Классическая механика
• сила Кориолиса
• Динамика (физика)
• Эскимосское йо-йо
• Пример: круговое движение
• Фиктивная сила
• Формулы Френе-Серре
• История центробежных и центростремительных сил
• Кинематика
• Кинетика
• Механика движения плоских частиц
• Ортогональные координаты
• Реактивная центробежная сила
• Статика

Дальнейшее чтение

• Сервей, Раймонд А.; Джуэтт, Джон В. (2004). Физика для ученых и инженеров (6-е изд.). Брукс/Коул. ISBN  978-0-534-40842-8 .
• Типлер, Пол (2004). Физика для ученых и инженеров: Механика, колебания и волны, Термодинамика (5-е изд.). У. Х. Фриман. ISBN  978-0-7167-0809-4 .
• Центростремительная сила против центробежной силы , из онлайн-урока по физике для экзамена Риджентс, проведенного школьным округом города Освего.

Внешние ссылки

• Заметки по физике и астрономии Гиперфизика в Университете штата Джорджия