Круговое движение

В физике круговое движение это движение объекта по окружности дуге — или вращение по окружности . Он может быть равномерным, с постоянной скоростью вращения и постоянной тангенциальной скоростью , или неравномерным, с изменяющейся скоростью вращения. Вращение вокруг неподвижной оси трехмерного тела предполагает круговое движение его частей. Уравнения движения описывают движение центра масс тела, находящегося на постоянном расстоянии от оси вращения . При круговом движении расстояние между телом и неподвижной точкой его поверхности остается прежним, т. е. тело считается жестким .

Примеры кругового движения включают: специальные орбиты спутников вокруг Земли ( круговые орбиты ), лопасти потолочного вентилятора, вращающиеся вокруг ступицы, камень, привязанный к веревке и раскачивающийся по кругу, автомобиль, поворачивающий по кривой в гоночная трасса , электрон, движущийся перпендикулярно однородному магнитному полю , и шестерня, вращающаяся внутри механизма.

объекта Поскольку вектор скорости постоянно меняет направление, движущийся объект испытывает ускорение под действием центростремительной силы в направлении центра вращения. Без этого ускорения объект двигался бы прямолинейно, согласно законам движения Ньютона .

Равномерное круговое движение

Рисунок 2: Векторы скорости в момент времени $t$ и момент времени $t + dt$ перемещаются с орбиты слева в новые положения, где их хвосты совпадают, справа. Поскольку скорость фиксирована по величине при $v = r ω$ , векторы скорости также огибают круговую траекторию с угловой скоростью $ω$ . При $dt \to 0$ вектор ускорения $a$ становится перпендикулярным $v$ , что означает, что он указывает на центр орбиты в круге слева. Угол $ω dt$ — это очень малый угол между двумя скоростями, который стремится к нулю при $dt \to 0$ .

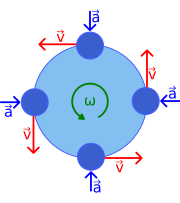
В физике круговой равномерное круговое движение описывает движение тела, проходящего по траектории с постоянной скоростью . Поскольку тело описывает круговое движение, его расстояние от оси вращения всегда остается постоянным. Хотя скорость тела постоянна, его скорость не является постоянной: скорость, векторная величина, зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускорения; это центростремительное ускорение имеет постоянную величину и всегда направлено к оси вращения. Это ускорение, в свою очередь, создается центростремительной силой , которая также постоянна по величине и направлена к оси вращения.

При вращении вокруг неподвижной оси , твердого тела не пренебрежимо малом по сравнению с радиусом пути, каждая частица тела описывает равномерное круговое движение с одинаковой угловой скоростью, но со скоростью и ускорением, меняющимися в зависимости от положение относительно оси.

Формула

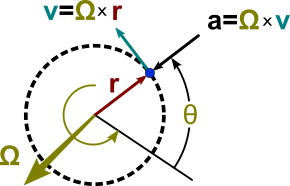
Для движения по кругу радиуса $r$ длина окружности равна $C = 2 πr$ . Если период одного оборота равен $T$ , угловая скорость вращения, также известная как угловая скорость , $ω$ равна: $\omega ={\frac {2\pi }{T}}=2\pi f={\frac {d\theta }{dt}}$ единицы измерения — радианы в секунду.

Скорость тела, движущегося по окружности, равна: $v={\frac {2\pi r}{T}}=\omega r$

Угол $θ,$ выметаемый за время $t,$ равен: $\theta =2\pi {\frac {t}{T}}=\omega t$

Угловое ускорение α $:$ частицы равно $\alpha ={\frac {d\omega }{dt}}$

В случае равномерного кругового движения $α$ будет равно нулю.

Ускорение, вызванное изменением направления, равно: $a_{c}={\frac {v^{2}}{r}}=\omega ^{2}r$

Центростремительную и : центробежную силу также можно найти с помощью ускорения $F_{c}={\dot {p}}\mathrel {\overset {{\dot {m}}=0}{=}} ma_{c}={\frac {mv^{2}}{r}}$

Векторные зависимости показаны на рисунке 1. Ось вращения изображена в виде вектора $ω,$ перпендикулярного плоскости орбиты и имеющего величину $ω = dθ / dt$ . Направление $ω$ выбирается по правилу правой руки . При таком соглашении об изображении вращения скорость определяется векторным векторным произведением как $\mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r} ,$ который представляет собой вектор, перпендикулярный как $ω$ , $так и r (t)$ , касательный к орбите и имеющий величину $ω r$ . Аналогично, ускорение определяется выражением $\mathbf {a} ={\boldsymbol {\omega }}\times \mathbf {v} ={\boldsymbol {\omega }}\times \left({\boldsymbol {\omega }}\times \mathbf {r} \right),$ который является вектором, перпендикулярным как $ω$ , так и $v (t)$ величины $ω | в | = ω 2 r$ и направлена точно противоположно $r (t)$ . ^[1]

В простейшем случае скорость, масса и радиус постоянны.

Рассмотрим тело массой один килограмм, движущееся по кругу радиусом один метр с угловой скоростью один радиан в секунду .

Скорость . 1 метр в секунду
внутрь Ускорение составляет 1 метр в секунду в квадрате, $v. 2 / р$ .
На него действует центростремительная сила величиной 1 килограмм-метр в секунду квадратную, что составляет 1 ньютон .
Импульс . тела равен 1 кг·м·с ⁻¹.
Момент инерции 1 кг·м. ².
Угловой момент 1 кг·м. ²·с ⁻¹.
Кинетическая энергия равна 0,5 джоуля .
Окружность составляет орбиты (~6,283) метра 2 $π$ .
Период движения равен 2π $секунд$ за один оборот .
Частота π 2 $)$ равна ( ⁻¹ герц .

В полярных координатах

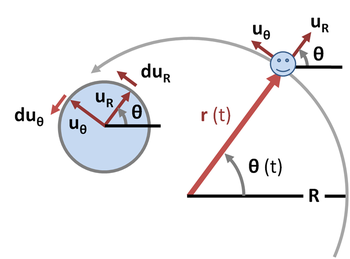
При круговом движении тело движется по кривой, которую можно описать в полярной системе координат как фиксированное расстояние $R$ от центра орбиты, принятого за начало координат, ориентированное под углом $θ (t)$ от некоторого опорного направления. смещения. См. рисунок 4. Вектор $\mathbf {r}$ — радиальный вектор от начала координат до местоположения частицы: $\mathbf {r} (t)=R{\hat {\mathbf {u} }}_{R}(t)\,,$ где ${\hat {\mathbf {u} }}_{R}(t)$ - единичный вектор, параллельный радиус-вектору в момент времени $t$ и направленный от начала координат. Удобно ввести единичный вектор ортогональный , ${\hat {\mathbf {u} }}_{R}(t)$ также, а именно ${\hat {\mathbf {u} }}_{\theta }(t)$ . принято ориентироваться ${\hat {\mathbf {u} }}_{\theta }(t)$ чтобы указать направление движения по орбите.

Скорость является производной перемещения по времени: $\mathbf {v} (t)={\frac {d}{dt}}\mathbf {r} (t)={\frac {dR}{dt}}{\hat {\mathbf {u} }}_{R}(t)+R{\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}\,.$

Поскольку радиус окружности постоянен, радиальная составляющая скорости равна нулю. Единичный вектор ${\hat {\mathbf {u} }}_{R}(t)$ имеет не зависящую от времени величину, равную единице, поэтому при изменении времени его кончик всегда лежит на окружности единичного радиуса с углом $θ$ , таким же, как угол $\mathbf {r} (t)$ . Если смещение частицы поворачивается на угол $dθ$ за время $dt$ , то же самое происходит и с перемещением частицы. ${\hat {\mathbf {u} }}_{R}(t)$ , описывающая дугу на единичной окружности величиной $dθ$ . См. единичный круг слева на рисунке 4. Следовательно: ${\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}={\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)\,,$ где направление изменения должно быть перпендикулярно ${\hat {\mathbf {u} }}_{R}(t)$ (или, другими словами, вдоль ${\hat {\mathbf {u} }}_{\theta }(t)$ ), потому что любое изменение $d{\hat {\mathbf {u} }}_{R}(t)$ в направлении ${\hat {\mathbf {u} }}_{R}(t)$ изменил бы размер ${\hat {\mathbf {u} }}_{R}(t)$ . Знак положительный, поскольку увеличение $dθ$ подразумевает объект и ${\hat {\mathbf {u} }}_{R}(t)$ двинулись в направлении ${\hat {\mathbf {u} }}_{\theta }(t)$ .Следовательно, скорость становится: $\mathbf {v} (t)={\frac {d}{dt}}\mathbf {r} (t)=R{\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}=R{\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)=R\omega {\hat {\mathbf {u} }}_{\theta }(t)\,.$

Ускорение тела также можно разбить на радиальную и тангенциальную составляющие. Ускорение является производной скорости по времени: ${\begin{aligned}\mathbf {a} (t)&={\frac {d}{dt}}\mathbf {v} (t)={\frac {d}{dt}}\left(R\omega {\hat {\mathbf {u} }}_{\theta }(t)\right)\\&=R\left({\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)+\omega {\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}\right)\,.\end{aligned}}$

Производная по времени ${\hat {\mathbf {u} }}_{\theta }(t)$ находится так же, как и для ${\hat {\mathbf {u} }}_{R}(t)$ . Снова, ${\hat {\mathbf {u} }}_{\theta }(t)$ — единичный вектор, и его кончик описывает единичную окружность с углом $π /2 + θ$ . Следовательно, увеличение угла $dθ$ на $\mathbf {r} (t)$ подразумевает ${\hat {\mathbf {u} }}_{\theta }(t)$ трассирует дугу величины $dθ$ , и поскольку ${\hat {\mathbf {u} }}_{\theta }(t)$ ортогонален ${\hat {\mathbf {u} }}_{R}(t)$ , у нас есть: ${\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}=-{\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{R}(t)=-\omega {\hat {\mathbf {u} }}_{R}(t)\,,$ где отрицательный знак необходимо сохранить ${\hat {\mathbf {u} }}_{\theta }(t)$ ортогонально ${\hat {\mathbf {u} }}_{R}(t)$ . (В противном случае угол между ${\hat {\mathbf {u} }}_{\theta }(t)$ и ${\hat {\mathbf {u} }}_{R}(t)$ будет уменьшаться с увеличением $dθ$ .) См. единичный круг слева на рисунке 4. Следовательно, ускорение равно: ${\begin{aligned}\mathbf {a} (t)&=R\left({\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)+\omega {\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}\right)\\&=R{\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)-\omega ^{2}R{\hat {\mathbf {u} }}_{R}(t)\,.\end{aligned}}$

Центростремительным ускорением является радиальная составляющая, направленная радиально внутрь: $\mathbf {a} _{R}(t)=-\omega ^{2}R{\hat {\mathbf {u} }}_{R}(t)\,,$ а тангенциальная составляющая меняет величину скорости: $\mathbf {a} _{\theta }(t)=R{\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)={\frac {dR\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)={\frac {d\left|\mathbf {v} (t)\right|}{dt}}{\hat {\mathbf {u} }}_{\theta }(t)\,.$

Использование комплексных чисел

Круговое движение можно описать с помощью комплексных чисел . Пусть $ось x$ — действительная ось, а $y$ ось — мнимая ось. Тогда положение тела можно представить как $z$ , сложный «вектор»: $z=x+iy=R\left(\cos[\theta (t)]+i\sin[\theta (t)]\right)=Re^{i\theta (t)}\,,$ где $я$ — мнимая единица измерения , а $\theta (t)$ — аргумент комплексного числа как функция времени, $t$ .

Поскольку радиус постоянный: ${\dot {R}}={\ddot {R}}=0\,,$ где точка означает дифференциацию по времени.

В этих обозначениях скорость становится: $v={\dot {z}}={\frac {d}{dt}}\left(Re^{i\theta [t]}\right)=R{\frac {d}{dt}}\left(e^{i\theta [t]}\right)=Re^{i\theta (t)}{\frac {d}{dt}}\left(i\theta [t]\right)=iR{\dot {\theta }}(t)e^{i\theta (t)}=i\omega Re^{i\theta (t)}=i\omega z$ и ускорение станет: ${\begin{aligned}a&={\dot {v}}=i{\dot {\omega }}z+i\omega {\dot {z}}=\left(i{\dot {\omega }}-\omega ^{2}\right)z\\&=\left(i{\dot {\omega }}-\omega ^{2}\right)Re^{i\theta (t)}\\&=-\omega ^{2}Re^{i\theta (t)}+{\dot {\omega }}e^{i{\frac {\pi }{2}}}Re^{i\theta (t)}\,.\end{aligned}}$

Первый член направлен противоположно вектору смещения, а второй перпендикулярен ему, как и предыдущие результаты, показанные ранее.

Скорость

На рисунке 1 показаны векторы скорости и ускорения для равномерного движения в четырех разных точках орбиты. Поскольку скорость $v$ касается окружности, никакие две скорости не указывают в одном направлении. Хотя объект имеет постоянную скорость , его направление постоянно меняется. Это изменение скорости вызвано ускорением $а$ , величина которого (как и скорость) остается постоянной, но направление которого также постоянно меняется. Ускорение направлено радиально внутрь ( центростремительно ) и перпендикулярно скорости. Это ускорение известно как центростремительное ускорение.

Для траектории радиуса $r$ на угол $θ$ при повороте пройденное расстояние по периферии орбиты равно $s = rθ$ . Следовательно, скорость движения по орбите равна $v=r{\frac {d\theta }{dt}}=r\omega ,$ где угловая скорость вращения равна $ω$ . (При перестановке $ω = v / r$ .) Таким образом, $v$ является константой, и вектор скорости $v$ также вращается с постоянной величиной $v$ , с той же угловой скоростью $ω$ .

Релятивистское круговое движение

В этом случае вектор трех ускорений перпендикулярен вектору трех скоростей: $\mathbf {u} \cdot \mathbf {a} =0.$ и квадрат собственного ускорения, выраженный в виде скалярного инварианта, одинакового во всех системах отсчета, $\alpha ^{2}=\gamma ^{4}a^{2}+\gamma ^{6}\left(\mathbf {u} \cdot \mathbf {a} \right)^{2},$ становится выражением кругового движения, $\alpha ^{2}=\gamma ^{4}a^{2}.$ или, взяв положительный квадратный корень и используя тройное ускорение, мы придем к правильному ускорению для кругового движения: $\alpha =\gamma ^{2}{\frac {v^{2}}{r}}.$

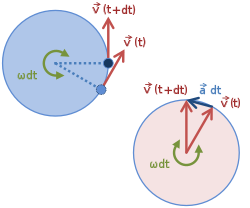
Ускорение

Левый круг на рисунке 2 — это орбита, показывающая векторы скорости в два соседних момента времени. Справа эти две скорости сдвинуты так, что их хвосты совпадают. Поскольку скорость постоянна, векторы скорости справа с течением времени очерчивают круг. Для угла стреловидности $dθ = ω dt$ изменение $v$ представляет собой вектор, расположенный под прямым углом к $v$ и имеющий величину $v dθ$ , что, в свою очередь, означает, что величина ускорения определяется выражением $a_{c}=v{\frac {d\theta }{dt}}=v\omega ={\frac {v^{2}}{r}}$

Центростремительное ускорение для некоторых значений радиуса и величины скорости
$\| v \|$ $р$		1 м/с 3,6 км/ч 2,2 мили в час	2 м/с 7,2 км/ч 4,5 миль в час	5 м/с 18 км/ч 11 миль в час	10 м/с 36 км/ч 22 мили в час	20 м/с 72 км/ч 45 миль в час	50 м/с 180 км/ч 110 миль в час	100 м/с 360 км/ч 220 миль в час
$\| v \|$ $р$		Медленная прогулка		Велосипед		Городской автомобиль		Высший пилотаж
10 см 3,9 дюйма	Лаборатория центрифуга	10 м/с ² 1,0 г	40 м/с ² 4,1 г	250 м/с ² 25 г	1,0 км/с ² 100 г	4,0 км/с ² 410 г	25 км/с ² 2500 г	100 км/с ² 10000 г
20 см 7,9 дюйма		5,0 м/с ² 0,51 г	20 м/с ² 2,0 г	130 м/с ² 13 г	500 м/с ² 51 г	2,0 км/с ² 200 г	13 км/с ² 1300 г	50 км/с ² 5100 г
50 см 1,6 фута		2,0 м/с ² 0,20 г	8,0 м/с ² 0,82 г	50 м/с ² 5,1 г	200 м/с ² 20 г	800 м/с ² 82 г	5,0 км/с ² 510 г	20 км/с ² 2000 г
1 м 3,3 фута	Детская площадка карусель	1,0 м/с ² 0,10 г	4,0 м/с ² 0,41 г	25 м/с ² 2,5 г	100 м/с ² 10 г	400 м/с ² 41 г	2,5 км/с ² 250 г	10 км/с ² 1000 г
2 м 6,6 футов		500 мм/с ² 0,051 г	2,0 м/с ² 0,20 г	13 м/с ² 1,3 г	50 м/с ² 5,1 г	200 м/с ² 20 г	1,3 км/с ² 130 г	5,0 км/с ² 510 г
5 м 16 футов		200 мм/с ² 0,020 г	800 мм/с ² 0,082 г	5,0 м/с ² 0,51 г	20 м/с ² 2,0 г	80 м/с ² 8,2 г	500 м/с ² 51 г	2,0 км/с ² 200 г
10 м 33 фута	Американские горки вертикальная петля	100 мм/с ² 0,010 г	400 мм/с ² 0,041 г	2,5 м/с ² 0,25 г	10 м/с ² 1,0 г	40 м/с ² 4,1 г	250 м/с ² 25 г	1,0 км/с ² 100 г
20 м 66 футов		50 мм/с ² 0,0051 г	200 мм/с ² 0,020 г	1,3 м/с ² 0,13 г	5,0 м/с ² 0,51 г	20 м/с ² 2 г	130 м/с ² 13 г	500 м/с ² 51 г
50 м 160 футов		20 мм/с ² 0,0020 г	80 мм/с ² 0,0082 г	500 мм/с ² 0,051 г	2,0 м/с ² 0,20 г	8,0 м/с ² 0,82 г	50 м/с ² 5,1 г	200 м/с ² 20 г
100 м 330 футов	Автострада съезд	10 мм/с ² 0,0010 г	40 мм/с ² 0,0041 г	250 мм/с ² 0,025 г	1,0 м/с ² 0,10 г	4,0 м/с ² 0,41 г	25 м/с ² 2,5 г	100 м/с ² 10 г
200 м 660 футов		5,0 мм/с ² 0,00051 г	20 мм/с ² 0,0020 г	130 м/с ² 0,013 г	500 мм/с ² 0,051 г	2,0 м/с ² 0,20 г	13 м/с ² 1,3 г	50 м/с ² 5,1 г
500 м 1600 футов		2,0 мм/с ² 0,00020 г	8,0 мм/с ² 0,00082 г	50 мм/с ² 0,0051 г	200 мм/с ² 0,020 г	800 мм/с ² 0,082 г	5,0 м/с ² 0,51 г	20 м/с ² 2,0 г
1 км 3300 футов	Высокоскоростной железная дорога	1,0 мм/с ² 0,00010 г	4,0 мм/с ² 0,00041 г	25 мм/с ² 0,0025 г	100 мм/с ² 0,010 г	400 мм/с ² 0,041 г	2,5 м/с ² 0,25 г	10 м/с ² 1,0 г

Неравномерный

При неравномерном круговом движении объект движется по круговой траектории с переменной скоростью . Поскольку скорость меняется, существует тангенциальное ускорение помимо нормального ускорения .

При неравномерном круговом движении результирующее ускорение (а) направлено вдоль направления $Δv .$ , которое направлено внутрь круга, но не проходит через его центр (см. рисунок) Чистое ускорение можно разделить на две составляющие: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное или радиальное ускорение. В отличие от тангенциального ускорения, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении.

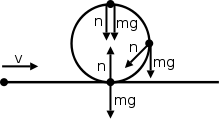
При неравномерном круговом движении нормальная сила не всегда направлена в направлении, противоположном направлению веса . Вот пример, когда объект движется по прямому пути, а затем снова возвращается на прямой путь.

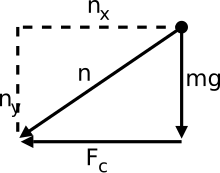
На этой диаграмме показана нормальная сила, направленная в других направлениях, а не противоположная силе веса. Нормальная сила на самом деле представляет собой сумму радиальной и тангенциальной сил. За тангенциальную силу здесь отвечает составляющая силы веса (силой трения мы пренебрегли). Радиальная сила (центростремительная сила) возникает из-за изменения направления скорости, как обсуждалось ранее.

При неравномерном круговом движении нормальная сила и вес могут указывать в одном направлении. Обе силы могут быть направлены вниз, но объект будет оставаться на круговой траектории, не падая прямо вниз. Во-первых, давайте посмотрим, почему нормальная сила может быть направлена вниз. Предположим, что на первой диаграмме объект — это человек, сидящий внутри плоскости, две силы направлены вниз только тогда, когда он достигает вершины круга. Причина этого в том, что нормальная сила представляет собой сумму касательной и центростремительной силы. Тангенциальная сила равна нулю вверху (поскольку работа не совершается, когда движение перпендикулярно направлению приложенной силы. Здесь сила веса перпендикулярна направлению движения объекта в верхней части круга), а центростремительная сила точки вниз, поэтому нормальная сила также будет направлена вниз. С логической точки зрения человек, путешествующий в самолете, окажется вверху круга вверх ногами. В этот момент сиденье человека фактически давит на человека, что является нормальной силой.

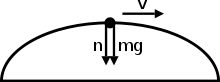
Причина, по которой объект не падает, если на него действует только направленная вниз сила, проста. Подумайте, что удерживает предмет после того, как его бросили. Когда объект подбрасывается в воздух, на объект действует только нисходящая сила гравитации Земли. Это не означает, что, подбросив предмет в воздух, он мгновенно упадет. Что удерживает этот объект в воздухе, так это его скорость . Первый из законов движения Ньютона объекта гласит, что инерция поддерживает его в движении, и поскольку объект в воздухе имеет скорость, он будет стремиться продолжать двигаться в этом направлении.

Изменение угловой скорости объекта, движущегося по круговой траектории, может быть достигнуто и в том случае, если вращающееся тело не имеет однородного распределения массы. Для неоднородных объектов необходимо подойти к задаче так. ^[2]

Можно вывести формулы скорости, ускорения и рывка, предполагая, что все переменные зависят от $t$ : $\mathbf {r} =R\mathbf {u} _{R}$

${\dot {\mathbf {u} }}_{R}=\omega \mathbf {u} _{\theta }$

${\dot {\mathbf {u} }}_{\theta }=-\omega \mathbf {u} _{R}$

$\mathbf {v} ={\frac {d}{dt}}\mathbf {r} ={\dot {\mathbf {r} }}={\dot {R}}\mathbf {u} _{R}+R\omega \mathbf {u} _{\theta }$

$\mathbf {a} ={\frac {d}{dt}}\mathbf {v} ={\dot {\mathbf {v} }}={\ddot {R}}\mathbf {u} _{R}+\left({\dot {R}}\omega \mathbf {u} _{\theta }+{\dot {R}}\omega \mathbf {u} _{\theta }\right)+R{\dot {\omega }}\mathbf {u} _{\theta }-R\omega ^{2}\mathbf {u} _{R}$

$\mathbf {j} ={\frac {d}{dt}}\mathbf {a} ={\dot {\mathbf {a} }}={\dot {\ddot {R}}}\mathbf {u} _{R}+{\ddot {R}}\omega \mathbf {u} _{\theta }+\left(2{\ddot {R}}\omega \mathbf {u} _{\theta }+2{\dot {R}}{\dot {\omega }}\mathbf {u} _{\theta }-2{\dot {R}}\omega ^{2}\mathbf {u} _{R}\right)+{\dot {R}}{\dot {\omega }}\mathbf {u} _{\theta }+R{\ddot {\omega }}\mathbf {u} _{\theta }-R{\dot {\omega }}\omega \mathbf {u} _{R}-{\dot {R}}\omega ^{2}\mathbf {u} _{R}-R2{\dot {\omega }}\omega \mathbf {u} _{R}-R\omega ^{3}\mathbf {u} _{\theta }$

$\mathbf {j} =\left({\dot {\ddot {R}}}-3{\dot {R}}\omega ^{2}-3R{\dot {\omega }}\omega \right)\mathbf {u} _{R}+\left(3{\ddot {R}}\omega +3{\dot {R}}{\dot {\omega }}+R{\ddot {\omega }}-R\omega ^{3}\right)\mathbf {u} _{\theta }$

Дальнейшие преобразования могут включать $curvature=c={\frac {1}{R}},\omega ={\frac {v}{R}}=vc$ и соответствующие производные: ${\begin{aligned}{\dot {R}}&=-{\frac {\dot {c}}{c^{2}}}\\{\ddot {R}}&={\frac {2\left({\dot {c}}\right)^{2}}{c^{3}}}-{\frac {\ddot {c}}{c^{2}}}\\{\dot {\omega }}&={\frac {{\dot {v}}R-{\dot {R}}v}{R^{2}}}={\dot {v}}c+v{\dot {c}}\\\end{aligned}}$

Приложения

Решение приложений, связанных с неравномерным круговым движением, включает анализ сил. При равномерном круговом движении единственной силой, действующей на объект, движущийся по кругу, является центростремительная сила. При неравномерном круговом движении на объект действуют дополнительные силы, обусловленные ненулевым тангенциальным ускорением. Хотя на объект действуют дополнительные силы, сумма всех сил, действующих на объект, должна быть равна центростремительной силе. ${\begin{aligned}F_{\text{net}}&=ma\\&=ma_{r}\\&={\frac {mv^{2}}{r}}\\&=F_{c}\end{aligned}}$

Радиальное ускорение используется при расчете общей силы. Тангенциальное ускорение не используется при расчете общей силы, поскольку оно не отвечает за удержание объекта на круговой траектории. Единственное ускорение, обеспечивающее движение объекта по кругу, — это радиальное ускорение. Поскольку сумма всех сил представляет собой центростремительную силу, рисовать центростремительную силу на диаграмме свободного тела нет необходимости и обычно не рекомендуется.

С использованием $F_{\text{net}}=F_{c}$ , мы можем нарисовать диаграммы свободного тела, чтобы перечислить все силы, действующие на объект, а затем установить их равными $F_{c}$ . После этого мы можем решить все, что неизвестно (это может быть масса, скорость, радиус кривизны, коэффициент трения, нормальная сила и т. д.). Например, изображение выше, показывающее объект в верхней части полукруга, будет выражаться как $F_{c}=n+mg$ .

При равномерном круговом движении полное ускорение объекта на круговой траектории равно радиальному ускорению. Из-за присутствия тангенциального ускорения при неравномерном круговом движении это уже не соответствует действительности. Чтобы найти полное ускорение объекта в неоднородной окружности, найдите векторную сумму тангенциального ускорения и радиального ускорения. ${\sqrt {a_{r}^{2}+a_{t}^{2}}}=a$

Радиальное ускорение по-прежнему равно ${\textstyle {\frac {v^{2}}{r}}}$ . Тангенциальное ускорение — это просто производная скорости в любой данной точке: ${\textstyle a_{t}={\frac {dv}{dt}}}$ . Эта корневая сумма квадратов отдельных радиальных и тангенциальных ускорений верна только для кругового движения; для общего движения внутри плоскости с полярными координатами $(r,\theta )$ , член Кориолиса ${\textstyle a_{c}=2\left({\frac {dr}{dt}}\right)\left({\frac {d\theta }{dt}}\right)}$ следует добавить в $a_{t}$ , тогда как радиальное ускорение становится ${\textstyle a_{r}={\frac {-v^{2}}{r}}+{\frac {d^{2}r}{dt^{2}}}}$ .

См. также

Ссылки

^ Кнудсен, Йенс М.; Хьёрт, Пол Г. (2000). Элементы ньютоновской механики: включая нелинейную динамику (3-е изд.). Спрингер. п. 96. ИСБН 3-540-67652-Х .
^ Гомес, RW; Эрнандес-Гомес, Джей-Джей; Маркина, В. (25 июля 2012 г.). «Прыгающий цилиндр на наклонной плоскости» . Евро. Дж. Физ . 33 (5). ИОП: 1359–1365. arXiv : 1204.0600 . Бибкод : 2012EJPh...33.1359G . дои : 10.1088/0143-0807/33/5/1359 . S2CID 55442794 . Проверено 25 апреля 2016 г.

Внешние ссылки

Physclips: Механика с анимацией и видеоклипами от Университета Нового Южного Уэльса.
Круговое движение — глава из онлайн-учебника «Механика» (2019). Бенджамина Кроуэлла
Circular Motion Lecture – видеолекция по КМ
[1] - онлайн-учебник с различным анализом кругового движения.

[1] Кнудсен, Йенс М.; Хьёрт, Пол Г. (2000). Элементы ньютоновской механики: включая нелинейную динамику (3-е изд.). Спрингер. п. 96. ИСБН 3-540-67652-Х .

[2] Гомес, RW; Эрнандес-Гомес, Джей-Джей; Маркина, В. (25 июля 2012 г.). «Прыгающий цилиндр на наклонной плоскости» . Евро. Дж. Физ . 33 (5). ИОП: 1359–1365. arXiv : 1204.0600 . Бибкод : 2012EJPh...33.1359G . дои : 10.1088/0143-0807/33/5/1359 . S2CID 55442794 . Проверено 25 апреля 2016 г.

[1]

[2]