Рационализируемая стратегия
| Рационализируемость | |
|---|---|
| Концепция решения в теории игр | |
| Отношение | |
| Подмножество | Равновесие доминирующей стратегии |
| Суперсет | Равновесие Нэша |
| Значение | |
| Предложено | Д. Бернхейм и Д. Пирс |
| Пример | Соответствующие пенни |
Рационализируемость — это концепция решения в теории игр . Это наиболее либеральная из возможных концепций решения, которая по-прежнему требует, чтобы оба игрока были хотя бы в некоторой степени рациональны и знали, что другие игроки также в некоторой степени рациональны, т. е. что они не используют стратегии, в которых доминируют . Стратегия является рационализируемой, если существует некоторый возможный набор убеждений, которые оба игрока могут иметь относительно действий друг друга, которые все равно будут приводить к использованию данной стратегии.
Рационализируемость – это более широкое понятие, чем равновесие Нэша . Оба требуют, чтобы игроки оптимально реагировали на некоторые убеждения о действиях своих оппонентов, но равновесие Нэша требует, чтобы эти убеждения были правильными, а рационализируемость - нет. Рационализируемость была впервые независимо определена Бернхеймом (1984) и Пирсом (1984).
Определение
[ редактировать ]Начиная с игры нормальной формы , рационализируемый набор действий можно вычислить следующим образом:
- Начните с полного набора действий для каждого игрока.
- Удалите все доминирующие стратегии , то есть стратегии, которые «никогда не имеют смысла» (никогда не являются лучшим ответом на какие-либо убеждения о действиях оппонентов). Мотивацией этого шага является то, что ни один рациональный игрок никогда не выберет такие действия.
- действиях оппонентов Удалите все действия, которые никогда не являются лучшим ответом на какое-либо мнение об остальных — этот второй шаг оправдан, поскольку каждый игрок знает , что другие игроки рациональны.
- Продолжайте процесс до тех пор, пока дальнейшие действия не будут устранены.
В игре с конечным числом действий этот процесс всегда завершается и оставляет непустое множество действий для каждого игрока. Это рационализируемые действия.
Повторное устранение строго доминируемых стратегий (IESDS)
[ редактировать ]Итерированное устранение (или удаление, или удаление) доминируемых стратегий (также называемое IESDS, или IDSDS, или IRSDS) является одним из распространенных методов решения игр, который включает в себя итеративное удаление доминируемых стратегий. На первом этапе из пространства стратегий каждого из игроков удаляется не более одной доминируемой стратегии, поскольку ни один рациональный игрок никогда не будет использовать эти стратегии. В результате получается новая игра меньшего размера. Некоторые стратегии, над которыми раньше не доминировали, могут доминировать в более мелкой игре. Первый шаг повторяется, создается новая игра еще меньшего размера и так далее. Процесс останавливается, когда ни для одного игрока не найдена доминирующая стратегия. Этот процесс действителен, поскольку предполагается, что рациональность среди игроков общеизвестна , то есть каждый игрок знает, что остальные игроки рациональны, и каждый игрок знает, что остальные игроки знают, что он знает, что остальные игроки игроки рациональны, и так до бесконечности (см. Aumann, 1976).
Есть две версии этого процесса. Одна версия предполагает лишь устранение строго доминируемых стратегий. Если после завершения этого процесса у каждого игрока останется только одна стратегия, этот набор стратегий является уникальным равновесием Нэша. [1] Более того, многократное устранение строго доминируемых стратегий не зависит от пути. То есть, если в какой-то момент процесса существует несколько строго доминируемых стратегий, то для конечного результата не имеет значения, какие стратегии мы удалим первыми. [2]
Пошаговый пример удаления строгого доминирования:

- Для игрока 1 C строго доминирует игрок A. Следовательно, игрок 1 никогда не будет использовать стратегию C. Игрок 2 знает это. (см. рисунок 1 IESDS)
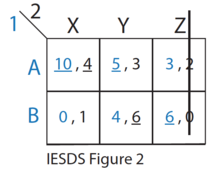
- Из оставшихся стратегий (см. рисунок 2 IESDS) над Z строго доминируют Y и X для игрока 2. Следовательно, игрок 2 никогда не будет использовать стратегию Z. Игрок 1 знает об этом.
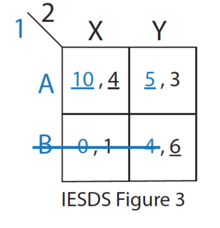
- Из оставшихся стратегий (см. рис. 3 IESDS) стратегия B строго доминируется А для Игрока 1. Следовательно, Игрок 1 никогда не будет играть в B. Игрок 2 знает это.
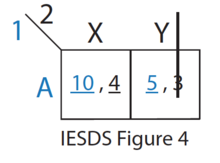
- Из остальных стратегий (см. рис. 4 IESDS) в Y строго доминирует X для игрока 2. Следовательно, игрок 2 никогда не будет играть в Y. Игрок 1 знает это.
- Осталась только одна рационализируемая стратегия {A,X}, которая приводит к выигрышу (10,4). Это единственное равновесие Нэша для этой игры.
Другая версия предполагает устранение как строго, так и слабо доминируемых стратегий. Если в конце процесса для каждого игрока существует единственная стратегия, этот набор стратегий также является равновесием Нэша . Однако, в отличие от первого процесса, устранение слабо доминируемых стратегий может устранить некоторые равновесия Нэша. В результате равновесие Нэша, найденное путем исключения стратегий со слабым доминированием, может быть не единственным равновесием Нэша. (В некоторых играх, если мы удаляем стратегии со слабым доминированием в другом порядке, мы можем получить другое равновесие Нэша.)
Пошаговый пример удаления слабого доминирования:
- Для Игрока 1 O строго доминирует N. Следовательно, Игрок 1 никогда не будет использовать стратегию O. Игрок 2 знает это. (см. Рисунок 5 IESDS)
- U слабо доминируется T для Игрока 2. Если Игрок 2 выбирает T, то окончательное равновесие будет (N,T)
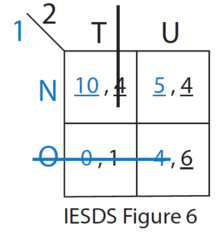
- Для Игрока 1 O строго доминирует N. Следовательно, Игрок 1 никогда не будет использовать стратегию O. Игрок 2 знает это. (см. Рисунок 6 IESDS)
- T слабо доминируется U для Игрока 2. Если Игрок 2 выбирает U, то окончательное равновесие будет (N,U)
В любом случае, если в результате многократного исключения доминируемых стратегий у каждого игрока остается только одна стратегия, игра называется игрой , разрешимой с доминированием .
Повторное исключение по смешанной стратегии
[ редактировать ]Бывают случаи, когда не существует чистой стратегии, которая доминировала бы над другой чистой стратегией, но смесь двух или более чистых стратегий может доминировать над другой стратегией. Это называется строго доминантными смешанными стратегиями. Некоторые авторы допускают таким образом устранение стратегий, в которых доминирует смешанная стратегия.
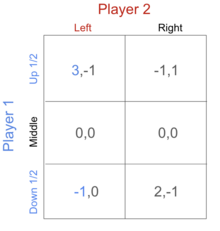
Пример 1:
В этом сценарии для игрока 1 не существует чистой стратегии, которая доминировала бы над другой чистой стратегией. Определим вероятность того, что игрок 1 сыграет, как p, и пусть p = 1/2 . Мы можем установить смешанную стратегию, в которой игрок 1 играет вверх и вниз с вероятностями ( 1 / 2 , 1/2 ) . Когда игрок 2 играет слева, то выигрыш игрока 1, использующего смешанную стратегию вверх и вниз, равен 1, когда игрок 2 играет справа, выигрыш игрока 1, использующего смешанную стратегию, равен 0,5. Таким образом, независимо от того, выберет ли игрок 2 левую или правую позицию, игрок 1 получит больше от этой смешанной стратегии «вверх» и «вниз», чем если бы игрок использовал среднюю стратегию. В этом случае нам следует исключить среднюю стратегию для игрока 1, поскольку в ней доминирует смешанная стратегия игры вверх и вниз с вероятностью ( 1 / 2 , 1 / 2 ).
Пример 2:
Мы можем продемонстрировать те же методы в более сложной игре и найти рациональные стратегии. В этом сценарии синий цвет представляет доминирующие числа в конкретной стратегии.

Пошаговое решение:
Для игрока 2 в X доминирует смешанная стратегия. 1/2 Y и 1 / 2 Z.
Ожидаемый выигрыш за стратегию игры 1 / 2 Y + 1 / 2 Z должно быть больше ожидаемого выигрыша при использовании чистой стратегии X, присваивая 1/2 и 1/2 как значения тестера. Аргумент в пользу доминирования смешанной стратегии может быть выдвинут, если существует хотя бы одна смешанная стратегия, допускающая доминирование.
Тестирование с 1/2 и 1/2 : получает следующее
Ожидаемый средний выигрыш 1/2 Y Стратегия : 1 / 2 (4+0+4) = 4
Ожидаемый средний выигрыш 1/2 Z : Стратегия 1 / 2 (0+5+5) = 5
Ожидаемый средний выигрыш чистой стратегии X: (1+1+3) = 5
Установите неравенство, чтобы определить, будет ли смешанная стратегия доминировать над чистой стратегией, основанной на ожидаемых выигрышах.
в 1/2 + Y ты 1/2 u Z ⩼ X
4 + 5 > 5
Смешанная стратегия 1/2 Y и 1/2 будет доминировать в чистой стратегии X для Игрока 2, и, таким образом , Z X можно исключить из рационализируемых стратегий для P2.
Для Игрока 1 в U доминирует чистая стратегия D.
Для игрока 2 в Y доминирует чистая стратегия Z.
В результате M доминирует над D для Игрока 1.
Тогда единственной рационализируемой стратегией для игроков 1 и 2 будет (M,Z) или (3,5).
Ограничения убеждений
[ редактировать ]| А | Б | |
|---|---|---|
| а | 1, 1 | 0, 0 |
| б | 0, 0 | 1, 1 |
Рассмотрим простую координационную игру ( платежная матрица справа). Игрок ряда может сыграть a, что игрок столбца может сыграть A , поскольку a — лучший ответ на A. если он может обоснованно полагать , Он может разумно полагать, что игрок в столбце может сыграть , если для игрока в столбце разумно полагать, что игрок в ряду может сыграть . А Она может поверить, что он сыграет а, если для нее разумно полагать, что он может сыграть а и т. д.
| С | Д | |
|---|---|---|
| с | 2, 2 | 0, 3 |
| д | 3, 0 | 1, 1 |
Это обеспечивает бесконечную цепочку последовательных убеждений, в результате которых игроки играют ( a , A ). Это делает ( a , A ) рационализируемой парой действий. Аналогичный процесс можно повторить для ( b , B ).
В качестве примера, когда не все стратегии рациональны, рассмотрим дилемму заключенного, изображенную слева. Игрок в ряд никогда не будет играть c , поскольку c не является лучшим ответом на любую стратегию игрока в столбце. По этой причине c не является рационализируемым.
| л | Р | |
|---|---|---|
| т | 3, - | 0, - |
| м | 0, - | 3, - |
| б | 1, - | 1, - |
И наоборот, для игр с двумя игроками набор всех рационализируемых стратегий можно найти путем многократного исключения строго доминируемых стратегий. Однако для того, чтобы этот метод работал, необходимо также учитывать строгое доминирование смешанных стратегий . Рассмотрим игру справа, в которой для простоты опущены выигрыши игрока-колонны. Обратите внимание, что «b» не находится под строгим доминированием «t» или «m» в чисто стратегическом смысле, но в нем все еще доминирует стратегия, которая смешала бы «t» и «m» с вероятностью каждого, равной 1/ 2. Это связано с тем, что при любом предположении о действиях игрока в колонне смешанная стратегия всегда будет приносить более высокий ожидаемый выигрыш. [3] Это означает, что «b» не является рационализируемым.
Более того, «b» — не лучший ответ ни на «L», ни на «R», ни на любое их сочетание. Это связано с тем, что действие, которое не поддается рационализации, никогда не может быть лучшим ответом на стратегию любого противника (чистую или смешанную). Это подразумевало бы другую версию предыдущего метода поиска рационализируемых стратегий, поскольку они выдерживают многократное устранение стратегий, которые никогда не являются лучшим ответом (в чистом или смешанном смысле).
Однако в играх с участием более двух игроков могут существовать стратегии, которые не являются строго доминируемыми, но которые никогда не могут быть лучшим ответом. Путем многократного исключения всех таких стратегий можно найти рационализируемые стратегии для многопользовательской игры.
Рационализируемость и равновесия Нэша
[ редактировать ]Можно легко доказать, что равновесие Нэша является рационализируемым равновесием; однако обратное неверно. Некоторые рационализируемые равновесия не являются равновесиями Нэша. Это делает концепцию рационализируемости обобщением концепции равновесия Нэша.
| ЧАС | Т | |
|---|---|---|
| час | 1, -1 | -1, 1 |
| т | -1, 1 | 1, -1 |
В качестве примера рассмотрим игру «Сопоставление монет», изображенную справа. В этой игре единственным равновесием Нэша является игра по строке h и t с равной вероятностью и игра по столбцу H и T. с равной вероятностью Однако все чистые стратегии в этой игре рационализируемы.
Рассмотрим следующее рассуждение: строка может воспроизводить h, если у нее есть основания полагать, что столбец будет H. воспроизводить Столбец может сыграть H, если для него разумно полагать, что эта строка будет играть t . Строка может сыграть t, если у нее есть основания полагать, что столбец будет T. играть Столбец может сыграть T, если у него есть основания полагать, что строка будет играть h (начиная цикл заново). Это обеспечивает бесконечный набор последовательных убеждений, что приводит к игре по строкам h . Аналогичный аргумент можно привести для воспроизведения строки t и для воспроизведения столбца либо H , либо T .
См. также
[ редактировать ]Сноски
[ редактировать ]- ^ Джоэл., Ватсон. Стратегия: введение в теорию игр (Второе изд.). Нью-Йорк. ISBN 9780393929348 .
- ^ Гильбоа, И.; Калай, Э.; Земель, Э. (1990). «О порядке устранения доминируемых стратегий» (PDF) . Письма об исследованиях операций . 9 (2): 85–89. дои : 10.1016/0167-6377(90)90046-8 .
- ^ Гиббонс, Роберт (1992). Букварь по теории игр . стр. 32–33.
Ссылки
[ редактировать ]- Бернхейм, Д. (1984) Рационализируемое стратегическое поведение. Эконометрика 52: 1007–1028.
- Фуденберг, Дрю и Жан Тироль (1993) Теория игр. Кембридж: MIT Press.
- Пирс, Д. (1984) Рационализируемое стратегическое поведение и проблема совершенства. Эконометрика 52: 1029–1050.
- Рэтклифф, Дж. (1992–1997) конспекты лекций по теории игр, §2.2: «Итеративное доминирование и рационализация».