Теорема Безу

Теорема Безу — это утверждение алгебраической геометрии, количества общих нулей от $n$ многочленов касающееся $n$ неопределённых. В своей первоначальной форме теорема утверждает, что в общем случае количество общих нулей равно произведению степеней многочленов . ^[1] Он назван в честь Этьена Безу .

В некоторых элементарных текстах теорема Безу относится только к случаю двух переменных и утверждает, что если две плоские алгебраические кривые степеней $d_{1}$ и $d_{2}$ не имеют общего компонента, они имеют $d_{1}d_{2}$ точки пересечения, учитываемые с учетом их кратности , включая точки на бесконечности и точки с комплексными координатами. ^[2]

В своей современной формулировке теорема утверждает, что если $N$ — число общих точек в алгебраически замкнутом поле из $n$ проективных гиперповерхностей, определяемых однородными полиномами от $n + 1$ неопределённых, то $N$ либо бесконечно, либо равно произведению степеней полиномов. Более того, конечный случай имеет место почти всегда.

В случае двух переменных и в случае аффинных гиперповерхностей, если не учитывать кратности и бесконечно удаленные точки, эта теорема дает лишь верхнюю оценку числа точек, которая почти всегда достигается. Эту границу часто называют границей Безу .

Теорема Безу является фундаментальной в компьютерной алгебре и эффективной алгебраической геометрии , показывая, что большинство задач имеют вычислительную сложность , которая, по крайней мере, экспоненциальна по числу переменных. Отсюда следует, что в этих областях наибольшая сложность, на которую можно надеяться, будет иметь место с алгоритмами, сложность которых полиномиальна по границе Безу.

История

В случае плоских кривых теорема Безу была по существу сформулирована Исааком Ньютоном в его доказательстве леммы 28 первого тома его «Начал» в 1687 году, где он утверждает, что две кривые имеют количество точек пересечения, определяемое произведением их степеней. ^[3]

Общая теорема была позже опубликована в 1779 году в Этьена Безу «Общей теории алгебраических уравнений» . Он предполагал, что уравнения «полные», что в современной терминологии можно было бы перевести как «общее» . Поскольку у полиномов общего положения нет бесконечно удаленных точек и все кратности равны единице, формулировка Безу правильна, хотя его доказательство не соответствует современным требованиям строгости. Это, а также тот факт, что концепция множественности пересечений находилась за пределами знаний его времени, привела к мнению, выраженному некоторыми авторами, что его доказательство не было ни правильным, ни первым доказательством, которое было дано. ^[4]

Доказательство утверждения, включающего кратности, требует точного определения кратностей пересечения и поэтому было невозможно до 20 века. Определения кратностей, данные в первой половине 20 в., включали непрерывные и бесконечно малые деформации . Отсюда следует, что доказательства этого периода применимы только к области комплексных чисел. Лишь в 1958 году Жан-Пьер Серр дал чисто алгебраическое определение кратностей, что привело к доказательству, справедливому для любого алгебраически замкнутого поля. ^[5]

Современные исследования, связанные с теоремой Безу, получили различные верхние оценки системы многочленов, используя другие свойства многочленов, такие как теорема Бернштейна-Кушниренко , или обобщили ее на большой класс функций, таких как функции Нэша . ^[6]

Заявление

Плоские кривые

Предположим, что X и Y — две плоские проективные кривые, определенные над полем F , не имеющие общей компоненты (это условие означает, что X и Y определяются полиномами без общего делителя положительной степени). Тогда общее число точек пересечения X и Y с координатами в алгебраически замкнутом поле E содержащем F , считая с их кратностями , равно произведению степеней X и Y. ,

Общий случай

Обобщение в более высоком измерении можно сформулировать как:

Пусть n проективных гиперповерхностей над алгебраически замкнутым полем даны в проективном пространстве размерности n , которые определяются n однородными многочленами от n + 1 переменных степеней $d_{1},\ldots ,d_{n}.$ Тогда либо число точек пересечения бесконечно, либо количество точек пересечения, считая с кратностью, равно произведению $d_{1}\cdots d_{n}.$ Если гиперповерхности находятся в относительном общем положении , то существуют $d_{1}\cdots d_{n}$ точки пересечения, все с кратностью 1.

Существуют различные доказательства этой теоремы, которые либо выражаются чисто алгебраическими терминами, либо используют язык алгебраической геометрии . Ниже представлены три алгебраических доказательства.

Теорема Безу была обобщена как так называемая мультиоднородная теорема Безу .

Аффинный случай

Аффинным случаем теоремы является следующее утверждение, доказанное в 1983 году Дэвидом Массером и Гисбертом Вюстхольцем . ^[7]

Рассмотрим $n$ аффинных гиперповерхностей , заданных над алгебраически замкнутым полем $n$ полиномами от $n$ переменных степеней $d_{1},\ldots ,d_{n}.$ Тогда либо число точек пересечения бесконечно, либо число точек пересечения, считая с их кратностями, не превосходит произведения $d_{1}\cdots d_{n}.$ Если гиперповерхности находятся в относительном общем положении , то существует ровно $d_{1}\cdots d_{n}$ точки пересечения, все с кратностью 1.

Эта версия не является прямым следствием общего случая, поскольку в аффинном пространстве возможно иметь конечное число точек пересечения с бесконечным количеством точек пересечения на бесконечности. Приведенное выше утверждение является частным случаем более общего утверждения, которое является результатом доказательства Массера и Вюстхольца.

Для формулировки общего результата следует вспомнить, что точки пересечения образуют алгебраическое множество и что существует конечное число точек пересечения тогда и только тогда, когда все компоненты пересечения имеют нулевую размерность (алгебраическое множество положительной размерности имеет бесконечность точек над алгебраически замкнутым полем). Точка пересечения называется изолированной , если она не принадлежит компоненте положительной размерности пересечения; терминология имеет смысл, поскольку изолированная точка пересечения имеет окрестности (для топологии Зариского или для обычной топологии в случае комплексных гиперповерхностей), не содержащие никакой другой точки пересечения.

Рассмотрим $n$ проективных гиперповерхностей, заданных над алгебраически замкнутым полем $n$ однородными полиномами от $n+1$ переменные, степени $d_{1},\ldots ,d_{n}.$ Тогда сумма кратностей их изолированных точек пересечения не превосходит произведения $d_{1}\cdots d_{n}.$ Результат остается справедливым для любого числа $m$ гиперповерхностей, если положить $d_{m+1}=0$ в случае $m<n,$ и, в противном случае, если кто-то заказывает степени за наличие $d_{2}\geq d_{3}\geq \cdots \geq d_{m}\geq d_{1}.$ То есть не существует изолированной точки пересечения, если $m<n,$ в противном случае оценка представляет собой произведение наименьшей степени и $n-1$ наибольшие степени.

Примеры (плоские кривые)

Две линии

Уравнение прямой в евклидовой плоскости линейно , то есть приравнивает нулю многочлен первой степени. Итак, граница Безу для двух линий равна $1$ , что означает, что две линии либо пересекаются в одной точке, либо не пересекаются. В последнем случае линии параллельны и встречаются в бесконечной точке .

В этом можно убедиться с помощью уравнений. Уравнение первой линии можно записать в форме наклона-пересечения. $y=sx+m$ или в проективных координатах $y=sx+mt$ (если линия вертикальная, можно поменять местами $x$ и $y$ ). Если уравнение второй линии (в проективных координатах) $ax+by+ct=0,$ заменив $sx+mt$ за $ты получаешь$ это $(a+bs)x+(c+bm)t=0.$ Если $a+bs\neq 0,$ можно получить $координату x$ точки пересечения $, решив последнее уравнение относительно x$ и положив $t = 1.$

Если $a+bs=0,$ то есть $s=-a/b,$ две линии параллельны и имеют одинаковый наклон. Если $m\neq -c/b,$ они различны, и замененное уравнение дает $t = 0$ . Это дает точку в бесконечности проективных координат $(1, s, 0)$ .

Линия и кривая

Как и выше, уравнение линии в проективных координатах можно записать как $y=sx+mt.$ Если кривая определяется в проективных координатах однородным полиномом $p(x,y,t)$ степени $n$ замена $y$ дает однородный полином степени $n$ по $x$ и $t$ . Фундаментальная теорема алгебры подразумевает, что ее можно учитывать с помощью линейных факторов. Каждый фактор дает соотношение $координат x$ и $t$ точки пересечения, а кратность фактора представляет собой кратность точки пересечения.

Если $t$ рассматривать как координату бесконечности , коэффициент, равный $t,$ представляет точку пересечения на бесконечности.

Если хотя бы одна частная производная многочлена $p$ не равна нулю в точке пересечения, то тангенс кривой в этой точке определен (см. Алгебраическая кривая § Касательная в точке ), а кратность пересечения больше единицы, если и только если линия касается кривой. Если все частные производные равны нулю, точка пересечения является особой точкой , а кратность пересечения равна как минимум двум.

Две конические секции

Два конических сечения обычно пересекаются в четырех точках, некоторые из которых могут совпадать. Чтобы правильно учесть все точки пересечения, может потребоваться разрешить комплексные координаты и включить точки бесконечной линии в проективную плоскость. Например:

Две окружности никогда не пересекаются более чем в двух точках плоскости, а теорема Безу предсказывает четыре. Несоответствие возникает из-за того, что каждая окружность проходит через одни и те же две комплексные точки на бесконечной прямой. Написание круга $(x-a)^{2}+(y-b)^{2}=r^{2}$ в однородных координатах получим $(x-az)^{2}+(y-bz)^{2}-r^{2}z^{2}=0,$ откуда ясно, что две точки $(1 : i : 0)$ и $(1 : - i : 0)$ лежат на каждой окружности. Когда две окружности вообще не пересекаются в реальной плоскости, два других пересечения имеют нереальные координаты, или, если окружности концентрические, то они встречаются ровно в двух точках на бесконечной линии с кратностью пересечения, равной двум.
Согласно теореме любая коника должна пересекать бесконечную линию в двух точках. Гипербола встречается с ним в двух вещественных точках, соответствующих двум направлениям асимптот. Эллипс пересекает его в двух комплексных точках, сопряженных друг с другом — в случае круга — в точках $(1: i : 0)$ и $(1: - i : 0)$ . Парабола пересекает его только в одной точке, но это точка касания и поэтому учитывается дважды.
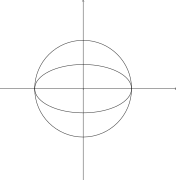
На следующих рисунках показаны примеры, в которых круг $x 2 + и 2 - 1 = 0$ встречается с другим эллипсом в меньшем количестве точек пересечения, поскольку хотя бы один из них имеет кратность больше единицы:

Пересечение эллипса и единичной окружности

Два пересечения кратности 2
$x^{2}+4y^{2}-1=0$
Два пересечения кратностей 3 и 1
$5x^{2}+6xy+5y^{2}+6y-5=0$
Одно пересечение кратности 4
$4x^{2}+y^{2}+6x+2=0$

Множественность

Концепция множественности является фундаментальной для теоремы Безу, поскольку она позволяет иметь равенство вместо гораздо более слабого неравенства.

Интуитивно понятно, что кратность общего нуля нескольких многочленов — это количество нулей, на которые может разбиться общий ноль при незначительном изменении коэффициентов. Например, касательная к кривой — это линия, разрезающая кривую в точке, которая разделяется на несколько точек, если линию слегка переместить. Обычно это число равно двум (обычным точкам), но может быть и больше (три для точек перегиба , четыре для точек волнистости и т. д.). Это число и есть «кратность контакта» касательной.

Это определение множественности посредством деформации было достаточным до конца XIX века, но имело несколько проблем, которые привели к более удобным современным определениям: деформациями трудно манипулировать; например, в случае корня одномерного многочлена , чтобы доказать, что кратность, полученная путем деформации, равна кратности соответствующего линейного множителя многочлена, нужно знать, что корни являются непрерывными функциями коэффициентов. Деформации нельзя использовать над полями характеристики положительной . Более того, бывают случаи, когда удобную деформацию определить трудно (например, в случае более чем двух плоских кривых, имеющих общую точку пересечения), и даже случаи, когда никакая деформация невозможна. ^{[ нужна ссылка ]}

В настоящее время, следуя Жану-Пьеру Серру , кратность обычно определяется как длина локального кольца, связанного с точкой, где рассматривается кратность. ^[5] Можно показать, что большинство конкретных определений являются частным случаем определения Серра.

В случае теоремы Безу общей теории пересечений можно избежать, поскольку существуют доказательства (см. ниже), которые связывают с каждым входным данными для теоремы многочлен от коэффициентов уравнений, который разлагается на линейные множители, каждый из которых соответствует единственная точка пересечения. Итак, кратность точки пересечения равна кратности соответствующего фактора. Доказательство того, что эта кратность равна кратности, полученной путем деформации, следует тогда из того факта, что точки пересечения и факторизованный многочлен непрерывно зависят от корней.

Доказательства

Используя полученный (плоские кривые)

Пусть $P$ и $Q$ — два однородных многочлена от неопределенных $x, y, t$ соответствующих степеней $p$ и $q$ . Их нули — однородные координаты двух проективных кривых . однородные координаты их точек пересечения являются общими нулями $P$ и $Q.$ Таким образом ,

Собирая вместе степени одной неопределенной величины, скажем, $y$ , можно получить одномерные многочлены, коэффициенты которых являются однородными многочленами от $x$ и $t$ .

По техническим причинам необходимо изменить координаты , чтобы степени по $y$ P $0$ и $Q$ были равны их сумме степеней ( $p$ и $q$ ), и каждая линия, проходящая через две точки пересечения, не проходила через точку $(0, 1, )$ (это означает, что никакие две точки не имеют одинаковой декартовой $x$ координаты .

R Результирующий $x (x, t)$ P $:$ и $Q$ относительно $y$ представляет собой однородный полином по $и$ t $,$ который обладает следующим свойством $R(\alpha ,\tau )=0$ с $(\alpha ,\tau )\neq (0,0)$ тогда и только тогда, когда оно существует $\beta$ такой, что $(\alpha ,\beta ,\tau )$ является общим нулем $P$ и $Q$ (см. Результирующие § Нули ). Вышеуказанное техническое состояние гарантирует, что $\beta$ является уникальным. Первое приведенное выше техническое условие означает, что при определении равнодействующей используются степени $p$ и $q$ ; это означает, что степень $R$ равна $pq$ (см. Результирующий § Однородность ).

Поскольку $R$ — однородный многочлен от двух неопределённых, из фундаментальной теоремы алгебры следует, что $R$ — произведение $pq$ линейных многочленов. Если определить кратность общего нуля $P$ и $Q$ как количество вхождений соответствующего множителя в произведение, теорема Безу будет доказана.

Чтобы доказать, что кратность пересечения, которая только что была определена, равна определению в терминах деформации, достаточно заметить, что результирующая и, следовательно, ее линейные факторы являются непрерывными функциями коэффициентов $P$ и $Q$ .

Доказательство равенства с другими определениями кратностей пересечения зависит от технических особенностей этих определений и поэтому выходит за рамки этой статьи.

Использование $U$ -результата

В начале 20-го века Фрэнсис Сауэрби Маколей ввел многомерный результат (также известный как результат Маколея ) $n$ однородных многочленов от $n$ неопределенных, который является обобщением обычного результата двух многочленов. Результат Маколея представляет собой полиномиальную функцию коэффициентов $n$ однородных многочленов, которая равна нулю тогда и только тогда, когда многочлены имеют нетривиальный (то есть некоторый компонент ненулевой) общий нуль в алгебраически замкнутом поле, содержащем коэффициенты.

U $-$ результат является частным случаем результата Маколея, также введенного Маколеем. Даны $n$ однородных многочленов $f_{1},\ldots ,f_{n}$ в $n + 1$ неопределенном $x_{0},\ldots ,x_{n},$ U $-результат является$ результатом $f_{1},\ldots ,f_{n},$ и $U_{0}x_{0}+\cdots +U_{n}x_{n},$ где коэффициенты $U_{0},\ldots ,U_{n}$ являются вспомогательными неопределенными. -результат $U$ представляет собой однородный многочлен от $U_{0},\ldots ,U_{n},$ степень которого является произведением степеней $f_{i}.$

Хотя многомерный полином обычно неприводим , $U$ -результат можно разложить на линейные (в $U_{i}$ ) многочлены над алгебраически замкнутым полем, содержащим коэффициенты $f_{i}.$ Эти линейные коэффициенты соответствуют общим нулям $f_{i}$ следующим образом: к каждому общему нулю $(\alpha _{0},\ldots ,\alpha _{n})$ соответствует линейному коэффициенту $(\alpha _{0}U_{0}+\cdots +\alpha _{n}U_{n}),$ и наоборот.

Это доказывает теорему Безу, если кратность общего нуля определяется как кратность соответствующего линейного множителя $U$ -результата. Что касается предыдущего доказательства, то равенство этой кратности с определением путем деформации вытекает из непрерывности $U$ -результата как функции коэффициентов $f_{i}.$

Это доказательство теоремы Безу кажется самым старым доказательством, удовлетворяющим современным критериям строгости.

Используя степень идеала

Теорему Безу можно доказать методом повторения числа многочленов. воспользовавшись следующей теоремой.

Пусть $V$ — проективное алгебраическое размерности множество $\delta$ и степень $d_{1}$ , а $H$ — гиперповерхность (определяемая одним полиномом) степени $d_{2}$ , не содержащий ни одной неприводимой V $компоненты$ ; согласно этим гипотезам пересечение $V$ и $H$ имеет размерность $\delta -1$ и степень $d_{1}d_{2}.$

Для (набросков) доказательства с использованием рядов Гильберта см. Ряды Гильберта и полином Гильберта § Степень проективного многообразия и теорему Безу .

Помимо концептуального простого доказательства теоремы Безу, эта теорема имеет фундаментальное значение для теории пересечений , поскольку эта теория по существу посвящена изучению кратностей пересечений, когда гипотезы вышеупомянутой теоремы не применяются.

См. также

Мультиоднородная теорема Безу
Теорема AF + BG - Об алгебраических кривых, проходящих через все точки пересечения двух других кривых.
Теорема Бернштейна – Кушниренко - О количестве общих нулей полиномов Лорана.

Примечания

^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Теорема Безу» , Архив истории математики MacTutor , Университет Сент-Эндрюс
^ Фултон 1974 .
^ Ньютон 1966 .
^ Кирван, Фрэнсис (1992). Сложные алгебраические кривые . Соединенное Королевство: Издательство Кембриджского университета. ISBN 0-521-42353-8 .
^ Jump up to: Перейти обратно: ^а ^б Теплица 1965 года .
^ Раманакорайсина, Р. (1989). «Теорема Безу для функций Нэша» . Журнал чистой и прикладной алгебры . 61 (3): 295–301. дои : 10.1016/0022-4049(89)90080-7 .
^ Массер и Вюстхольц 1983 .

Ссылки

Фултон, Уильям (1974). Алгебраические кривые . Серия лекций по математике. В. А. Бенджамин. п. 112. ISBN 0-8053-3081-4 .
Массер, Дэвид ; Вюстхольц, Гисберт (1983). «Поля большой степени трансцендентности, порожденные значениями эллиптических функций». Математические изобретения . 72 (3). Спрингер: 407–464. Бибкод : 1983ИнМат..72..407М . дои : 10.1007/BF01398396 . S2CID 120947443 .
Ньютон, И. (1966), Principia Vol. I «Движение тел» (на основе 2-го издания Ньютона (1713 г.); переведено Эндрю Моттом (1729 г.) и отредактировано Флорианом Каджори (1934 г.), Беркли, Калифорния: University of California Press, ISBN 978-0-520-00928-8 Ньютона Альтернативный перевод более раннего (2-го) издания «Начал» .
Серр, Жан-Пьер (1965). Локальная алгебра и кратности: курсы в Коллеж де Франс, 1957–1958, написанные Пьером Габриэлем . Спрингер.

Внешние ссылки

[1] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Теорема Безу» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[FOOTNOTEFulton1974-2] Фултон 1974 .

[FOOTNOTENewton1966-3] Ньютон 1966 .

[4] Кирван, Фрэнсис (1992). Сложные алгебраические кривые . Соединенное Королевство: Издательство Кембриджского университета. ISBN 0-521-42353-8 .

[FOOTNOTESerre1965-5] Jump up to: Перейти обратно: ^а ^б Теплица 1965 года .

[6] Раманакорайсина, Р. (1989). «Теорема Безу для функций Нэша» . Журнал чистой и прикладной алгебры . 61 (3): 295–301. дои : 10.1016/0022-4049(89)90080-7 .

[FOOTNOTEMasserWüstholz1983-7] Массер и Вюстхольц 1983 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]