Капиллярное действие

Капиллярная вода течет вверх по пористому кирпичу высотой 225 мм после того, как его поместили в неглубокий поддон с водой. Указывается время, прошедшее после первого контакта с водой. С учетом увеличения веса расчетная пористость составляет 25%.

Капиллярное действие воды (полярной) по сравнению с ртутью (неполярной), в каждом случае по отношению к полярной поверхности, такой как стекло (≡Si–OH).

Капиллярное действие (иногда называемое капиллярностью , капиллярным движением , капиллярным подъемом , капиллярным эффектом или впитыванием ) — это процесс течения жидкости в узком пространстве вопреки или, по крайней мере, без помощи каких-либо внешних сил, таких как гравитация .

Эффект можно увидеть при втягивании жидкости между волосками кисти, в тонкой трубке, такой как соломинка , в пористых материалах, таких как бумага и гипс, в некоторых непористых материалах, таких как глина и сжиженный углерод. волокно , или в биологической клетке .

Это происходит из-за межмолекулярных сил между жидкостью и окружающими твердыми поверхностями. Если диаметр трубки достаточно мал, то сочетание поверхностного натяжения (которое вызывается сцеплением внутри жидкости) и сил сцепления между жидкостью и стенками контейнера приводит в движение жидкость.

Этимология

«Капилляр» происходит от латинского слова capillaris, что означает «волосы или похожие на них». Значение этого слова кроется в крошечном, похожем на волос диаметре капилляра.

История

Первое зарегистрированное наблюдение действия капилляров было сделано Леонардо да Винчи . Говорят, что бывший ученик Галилея исследовал Никколо Аджунти действие капилляров. В 1660 году капиллярное действие все еще было новинкой для ирландского химика Роберта Бойля , когда он сообщил, что «некоторые любознательные французы» заметили, что, когда капиллярную трубку погружают в воду, вода поднимается «на некоторую высоту в трубе». . Затем Бойль сообщил об эксперименте, в котором он окунул капиллярную трубку в красное вино, а затем подверг трубку частичному вакууму. Он обнаружил, что вакуум не оказывает заметного влияния на высоту жидкости в капилляре, поэтому поведение жидкостей в капиллярах обусловлено каким-то явлением, отличным от того, которое управляет ртутными барометрами.

Вскоре примеру Бойля последовали и другие. Некоторые (например, Оноре Фабри , Джейкоб Бернулли ) считал, что жидкости поднимаются в капиллярах, потому что воздух не может проникать в капилляры так же легко, как жидкости, поэтому давление воздуха внутри капилляров было ниже. Другие (например, Исаак Воссиус , Джованни Альфонсо Борелли , Луи Карре , Фрэнсис Хоксби , Иосия Вайтбрехт ) считал, что частицы жидкости притягиваются друг к другу и к стенкам капилляра.

Хотя экспериментальные исследования продолжались и в XVIII веке, успешное количественное лечение капиллярного действия не был достигнут до 1805 года двумя исследователями: Томасом Янгом из Соединенного Королевства. и Пьер-Симон Лаплас из Франции. Они вывели Юнга – Лапласа уравнение капиллярного действия . К 1830 году немецкий математик Карл Фридрих Гаусс определил граничные условия, управляющие капиллярным действием (т. е. условия на границе раздела жидкость-твердое тело). В 1871 году британский физик сэр Уильям Томсон (впоследствии лорд Кельвин) определил влияние мениска на жидкости давление пара — соотношение, известное как уравнение Кельвина . Немецкий физик Франц Эрнст Нейман (1798–1895) впоследствии определил взаимодействие двух несмешивающихся жидкостей.

Первая статья Альберта Эйнштейна , представленная в журнал Annalen der Physik в 1900 году, была посвящена капиллярности.

Явления и физика

Умеренная поднимающаяся влажность на внутренней стене

Эксперимент «Капиллярное течение» для исследования капиллярных течений и явлений на борту Международной космической станции.

Капиллярное проникновение в пористые среды имеет тот же динамический механизм, что и течение в полых трубках, поскольку обоим процессам противодействуют силы вязкости. Следовательно, обычным устройством, используемым для демонстрации этого явления, является капиллярная трубка . Когда нижний конец стеклянной трубки помещается в жидкость, например воду, образуется вогнутый мениск . Адгезия происходит между жидкостью и твердой внутренней стенкой, тянущей столб жидкости вперед до тех пор, пока не появится достаточная масса жидкости, чтобы гравитационные силы могли преодолеть эти межмолекулярные силы. Длина контакта (по краю) между верхней частью столба жидкости и трубкой пропорциональна радиусу трубки, а вес столба жидкости пропорционален квадрату радиуса трубки. Таким образом, узкая трубка будет протягивать столб жидкости дальше, чем более широкая трубка, при условии, что внутренние молекулы воды достаточно связаны с внешними.

Примеры

В искусственной среде ограниченное испарением капиллярное проникновение является причиной явления повышения влажности в бетоне и каменной кладке , в то время как в промышленности и диагностической медицине это явление все чаще используется в области микрофлюидики на основе бумаги .

В физиологии капиллярное действие имеет важное значение для дренажа постоянно вырабатываемой слезной жидкости из глаза. имеются два канальца крошечного диаметра Во внутреннем углу века , называемые также слезными протоками ; их отверстия можно увидеть невооруженным глазом внутри слезных мешков при вывернутых веках.

Впитывание – это поглощение жидкости материалом, подобно фитилю свечи.

Бумажные полотенца впитывают жидкость за счет капиллярного действия, позволяя жидкости переноситься с поверхности на полотенце. Маленькие поры губки действуют как маленькие капилляры, заставляя ее впитывать большое количество жидкости. Говорят, что некоторые текстильные ткани используют капиллярное действие для «отвода» пота от кожи. Их часто называют впитывающими тканями из-за капиллярных свойств свечей и ламп фитилей .

Капиллярное действие наблюдается в тонкослойной хроматографии , при которой растворитель движется вертикально вверх по пластине под действием капиллярных сил. В этом случае поры представляют собой промежутки между очень мелкими частицами.

Капиллярное действие притягивает чернила к кончикам перьевой ручки перьев из резервуара или картриджа внутри ручки.

В некоторых парах материалов, таких как ртуть и стекло, межмолекулярные силы внутри жидкости превышают силы между твердым телом и жидкостью, поэтому образуется выпуклый мениск, и капиллярное действие действует в обратном направлении.

В гидрологии капиллярное действие описывает притяжение молекул воды к частицам почвы. Капиллярное действие отвечает за перемещение грунтовых вод из влажных участков почвы в сухие. Различия в потенциале почвы ( $\Psi _{m}$) вызывают капиллярное действие в почве.

Практическим применением капиллярного действия является сифон капиллярного действия. Вместо полой трубки (как в большинстве сифонов) это устройство состоит из отрезка шнура из волокнистого материала (подойдет хлопковый шнур или веревка). После насыщения шнура водой один (утяжеленный) конец помещают в резервуар, наполненный водой, а другой конец – в приемный сосуд. Резервуар должен быть выше приемного сосуда. Подобный, но упрощенный капиллярный сифон состоит только из двух стержней из нержавеющей стали в форме крючков, поверхность которых гидрофильна, что позволяет воде смачивать узкие канавки между ними. За счет капиллярного действия и силы тяжести вода будет медленно перемещаться из резервуара в приемный сосуд. Это простое устройство можно использовать для полива комнатных растений, когда никого нет дома. Это свойство используется и при смазке паровозов : фитили из камвольной шерсти используются для всасывания масла из резервуаров в нагнетательные трубы, ведущие к подшипникам .

У растений и животных

Капиллярное действие наблюдается у многих растений и играет роль в транспирации . Вода поднимается по деревьям за счет ветвей; испарение на листьях, вызывающее разгерметизацию; вероятно, из-за осмотического давления, создаваемого у корней; и, возможно, в других местах внутри растения, особенно при сборе влаги воздушными корнями .

Капиллярное действие поглощения воды было описано у некоторых мелких животных, таких как Ligia Exotica. и ужасный Молох

Высота мениска

Капиллярный подъем жидкости в капилляре

Зависимость высоты воды в капилляре от диаметра капилляра

Высота h столба жидкости определяется законом Жюрина.

$h={{2\gamma \cos {\theta }} \over {\rho gr}},$

где $\scriptstyle \gamma$ жидкость-воздух - поверхностное натяжение (сила/единица длины), θ - угол контакта , ρ - плотность жидкости (масса/объем), g - местное ускорение силы тяжести (длина/квадрат времени). ), а r — радиус трубки.

Поскольку r находится в знаменателе, то чем тоньше пространство, в котором может перемещаться жидкость, тем дальше она поднимается. Аналогичным образом, более легкая жидкость и меньшая сила тяжести увеличивают высоту колонны.

Для стеклянной трубки, наполненной водой, на воздухе в стандартных лабораторных условиях γ = 0,0728 Н/м при 20   °С, ρ = 1000 кг/м. ³ , и g = 9,81 м/с ² . Поскольку вода растекается по чистому стеклу, эффективный равновесный контактный угол равен примерно нулю. Для этих значений высота водного столба равна

$h\approx {{1.48\times 10^{-5}\ {\mbox{m}}^{2}} \over r}.$

Таким образом, для стеклянной трубки радиусом 2 м (6,6 фута) в лабораторных условиях, указанных выше, вода поднимется на незаметные 0,007 мм (0,00028 дюйма). Однако для трубки радиусом 2 см (0,79 дюйма) вода поднимется на 0,7 мм (0,028 дюйма), а для трубки радиусом 0,2 мм (0,0079 дюйма) вода поднимется на 70 мм (2,8 дюйма).

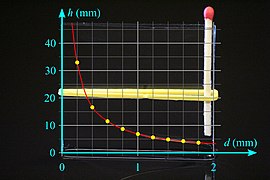
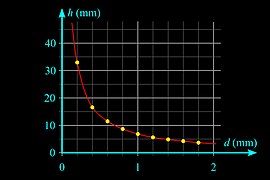
Капиллярный подъем жидкости между двумя стеклянными пластинами.

Произведение толщины слоя ( d ) и высоты возвышения ( h ) является постоянным ( d · h = константа), эти две величины обратно пропорциональны . Поверхность жидкости между плоскостями представляет собой гиперболу .

• Вода между двумя стеклянными пластинами
• 
• 
• 
• 
• 
• 

Транспорт жидкости в пористых средах

Капиллярное течение в кирпиче с сорбционной способностью 5,0 мм·мин. ^−1/2 и пористость 0,25.

Когда сухая пористая среда контактирует с жидкостью, она поглощает жидкость со скоростью, которая со временем уменьшается. При рассмотрении испарения проникновение жидкости достигнет предела, зависящего от параметров температуры, влажности и проницаемости. Этот процесс известен как испарение, ограниченное капиллярным проникновением. и широко наблюдается в обычных ситуациях, включая впитывание жидкости в бумагу и повышение влажности в бетонных или каменных стенах. Для стержневого сечения материала с площадью поперечного сечения A , смоченного с одного конца, совокупный объем V абсорбированной жидкости за время t равен

$V=AS{\sqrt {t}},$

где S – сорбционная способность среды, в м·с ^−1/2 или мм·мин ^−1/2 . Это соотношение зависимости от времени аналогично уравнению Уошберна для капилляров и пористых сред. Количество

$i={\frac {V}{A}}$

называется совокупным потреблением жидкости, имеющим размерность длины. Смоченная длина стержня, то есть расстояние между смоченным концом стержня и так называемым мокрым фронтом , зависит от доли f объема, занимаемого пустотами. Это число f — пористость среды; смоченная длина тогда равна

$x={\frac {i}{f}}={\frac {S}{f}}{\sqrt {t}}.$

используют величину S/f . Некоторые авторы в качестве сорбционной способности

Приведенное выше описание относится к случаю, когда гравитация и испарение не играют роли.

Сорбирующая способность является важным свойством строительных материалов, поскольку она влияет на количество поднимающейся влаги . Некоторые значения сорбционной способности строительных материалов приведены в таблице ниже.

Сорбционная способность выбранных материалов (источник: )

Материал	Сорбционная способность (мм·мин −1/2 )
Газобетон	0.50
Гипсовая штукатурка	3.50
Глиняный кирпич	1.16
миномет	0.70
Бетонный кирпич	0.20

См. также

• Число связи – безразмерное число в гидродинамике. Страницы с краткими описаниями целей перенаправления.
• Связанная вода – тонкий слой воды, окружающий минеральные поверхности.
• Капиллярная кайма - подповерхностный слой, в котором грунтовые воды просачиваются из уровня грунтовых вод под действием капилляров.
• Капиллярное давление - давление между двумя жидкостями из-за сил между жидкостями и стенками трубки.
• Капиллярная волна - волна на поверхности жидкости, в которой преобладает поверхностное натяжение.
• Капиллярные мостики - минимизированная поверхность жидкости, соединяющая два смачиваемых объекта.
• Гидроизоляция - тип контроля влажности в строительстве зданий.
• Закон Дарси - Уравнение, описывающее течение жидкости через пористую среду.
• Морозный цветок - тонкий слой льда, выдавленный из растения.
• Морозное пучение - набухание почвы вверх при замерзании.
• Индуистское молочное чудо - предполагаемые чудесные происшествия в 1995 году. Страницы с краткими описаниями целей перенаправления.
• Модель Крога
• Порозиметрия - измерение и характеристика пористости материала.
• Игольчатый лед - столб льда, образующийся, когда жидкие грунтовые воды поднимаются в замерзающий воздух.
• Поверхностное натяжение - тенденция поверхности жидкости сжиматься с целью уменьшения площади поверхности.
• Уравнение Уошберна - Уравнение, описывающее длину проникновения жидкости в капилляр с течением времени.
• Уравнение Юнга – Лапласа - описание разницы давлений на границе раздела в механике жидкости.

Дальнейшее чтение

• де Женн, Пьер-Жиль; Брошар-Вайарт, Франсуаза; Кере, Дэвид (2004). Капиллярность и явления смачивания . Спрингер Нью-Йорк. дои : 10.1007/978-0-387-21656-0 . ISBN  978-1-4419-1833-8 .