Демпфирование
| Часть серии о |
| Классическая механика |
|---|

В физических системах затухание — это потеря энергии за колебательной системы счет диссипации . [1] [2] Демпфирование — это воздействие внутри или на колебательную систему, которое приводит к уменьшению или предотвращению ее колебаний. [3] Примеры демпфирования включают вязкое демпфирование в жидкости (см. вязкое сопротивление ), поверхностное трение , излучение , [1] сопротивление в электронных генераторах , поглощение и рассеяние света в оптических генераторах . Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах и велосипедах. [4] (напр. Подвеска (механика) ). Демпфирование не следует путать с трением , которое представляет собой тип диссипативной силы, действующей на систему. Трение может вызывать или быть фактором демпфирования.
Коэффициент затухания — это безразмерная мера, описывающая, как затухают колебания в системе после возмущения. Многие системы демонстрируют колебательное поведение, когда они выводятся из положения статического равновесия . Например, масса, подвешенная на пружине, может, если ее потянуть и отпустить, подпрыгнуть вверх и вниз. При каждом отскоке система стремится вернуться в положение равновесия, но превышает его. Иногда потери (например, фрикционные) демпфируют систему и могут привести к постепенному затуханию амплитуды колебаний к нулю или затуханию . Коэффициент затухания — это мера, описывающая, насколько быстро затухают колебания от одного отскока к другому.
Коэффициент демпфирования — это системный параметр, обозначаемый ζ (« дзета »), который может варьироваться от незатухающего ( ζ = 0 ), недостаточно затухающего ( ζ < 1 ) через критическое затухание ( ζ = 1 ) до перезатухающего ( ζ > 1 ).
Поведение колебательных систем часто представляет интерес в самых разных дисциплинах, включая технику управления , химическую инженерию , машиностроение , структурную инженерию и электротехнику . Колеблющаяся физическая величина сильно различается, и это может быть раскачивание высокого здания на ветру или скорость электродвигателя , но нормализованный или безразмерный подход может быть удобен для описания общих аспектов поведения.
Случаи колебаний
[ редактировать ]В зависимости от степени присутствующего демпфирования система демонстрирует различное колебательное поведение и скорость.
- Если система пружина-масса полностью лишена потерь, масса будет колебаться бесконечно, причем каждый отскок будет иметь одинаковую высоту с предыдущим. Этот гипотетический случай называется незатухающим .
- Если бы система содержала большие потери, например, если эксперимент с пружиной и массой проводился в вязкой жидкости, масса могла бы медленно вернуться в исходное положение, даже не выходя за пределы. Этот случай называется перезатуханием .
- Обычно масса имеет тенденцию выйти за пределы своего исходного положения, а затем вернуться, снова пролетая мимо. При каждом выбросе часть энергии в системе рассеивается, и колебания затухают, стремясь к нулю. Этот случай называется недодемпфированным.
- Между случаями передемпфирования и недостаточного демпфирования существует определенный уровень демпфирования, при котором система просто не сможет проскочить и не совершит ни одного колебания. Этот случай называется критическим демпфированием . Ключевое различие между критическим демпфированием и чрезмерным демпфированием заключается в том, что при критическом демпфировании система возвращается в равновесие за минимальное время. [5]
Затухающая синусоидальная волна
[ редактировать ]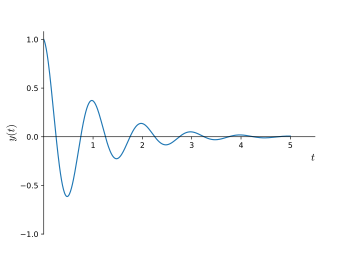
Затухающая синусоидальная волна или затухающая синусоида — это синусоидальная функция , амплитуда которой приближается к нулю с увеличением времени. Это соответствует недодемпфированному случаю затухающих систем второго порядка или недостаточно затухающим дифференциальным уравнениям второго порядка. [6] Затухающие синусоидальные волны часто встречаются в науке и технике , где гармонический генератор теряет энергию быстрее, чем ее подается.Истинная синусоидальная волна, начинающаяся в момент времени = 0, начинается в начале координат (амплитуда = 0). Косинусоидальная волна начинается с максимального значения из-за разницы фаз от синусоидальной волны. Данная синусоидальная форма сигнала может иметь промежуточную фазу, имеющую как синусоидальную, так и косинусоидальную составляющую. Термин «затухающая синусоидальная волна» описывает все такие затухающие сигналы, независимо от их начальной фазы.
Наиболее распространенной формой затухания, которую обычно принимают, является форма, встречающаяся в линейных системах. Эта форма представляет собой экспоненциальное затухание, при котором внешняя огибающая последовательных пиков представляет собой кривую экспоненциального затухания. То есть, когда вы соединяете точки максимума каждой последующей кривой, результат напоминает функцию экспоненциального затухания. Общее уравнение для экспоненциально затухающей синусоиды можно представить как: где:
- – мгновенная амплитуда в момент времени t ;
- – начальная амплитуда огибающей;
- — скорость затухания, обратная единицам времени независимой переменной t ;
- – фазовый угол при t = 0 ;
- - угловая частота .
Другие важные параметры включают в себя:
- Частота : , количество циклов в единицу времени. Выражается в обратных единицах времени. , или герц .
- Постоянная времени : , время уменьшения амплитуды в e раз .
- Период полураспада — это время, за которое огибающая экспоненциальной амплитуды уменьшается в 2 раза. Он равен что примерно .
- Коэффициент демпфирования: - безразмерная характеристика скорости затухания относительно частоты, приблизительно или точно .
- Q-фактор : – еще одна безразмерная характеристика величины демпфирования; высокий Q указывает на медленное затухание относительно колебаний.
Определение коэффициента демпфирования
[ редактировать ]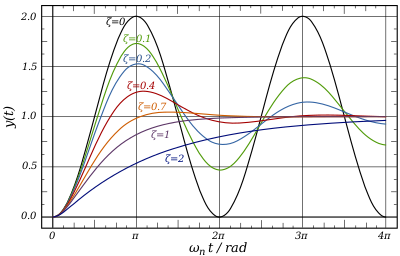
Коэффициент демпфирования — это параметр, обычно обозначаемый ζ (греческая буква дзета), [7] характеризующая частотную характеристику обыкновенного дифференциального уравнения второго порядка . Это особенно важно при изучении теории управления . Это также важно в гармоническом генераторе . В целом, системы с более высокими коэффициентами демпфирования (один или выше) будут демонстрировать больший эффект демпфирования. Системы с недостаточным демпфированием имеют значение меньше единицы. Системы с критическим демпфированием имеют коэффициент демпфирования, равный ровно 1 или, по крайней мере, очень близкий к нему.
Коэффициент демпфирования представляет собой математический способ выражения уровня демпфирования в системе относительно критического демпфирования. Для затухающего гармонического осциллятора с массой m , коэффициентом демпфирования c и жесткостью пружины k его можно определить как отношение коэффициента демпфирования в дифференциальном уравнении системы к критическому коэффициенту демпфирования:
где уравнение движения системы
- . [8]
и соответствующий критический коэффициент демпфирования равен
или
где
- – собственная частота системы.
Коэффициент демпфирования безразмерен и представляет собой отношение двух коэффициентов одинаковых единиц.
Вывод
[ редактировать ]Использование собственной частоты гармонического генератора и определение коэффициента демпфирования, приведенное выше, мы можем переписать это как:
Это уравнение является более общим, чем просто система масса-пружина, а также применимо к электрическим цепям и другим областям. Ее можно решить с помощью подхода
где C и s — комплексные константы, причем s удовлетворяет условиям
Два таких решения для двух значений s, удовлетворяющих уравнению, можно объединить, чтобы получить общие действительные решения с колебательными и затухающими свойствами в нескольких режимах:

- незатухающий
- Является ли тот случай, когда соответствует незатухающему простому гармоническому осциллятору, и в этом случае решение имеет вид , как и ожидалось. Этот случай чрезвычайно редок в мире природы, и наиболее близкими примерами являются случаи, когда трение целенаправленно снижалось до минимальных значений.
- Недостаточно демпфированный
- Если s — пара комплексных значений, то каждый член комплексного решения представляет собой затухающую экспоненту в сочетании с колебательной частью, которая выглядит как . Этот случай имеет место для и называется недостаточно демпфированным (например, банджи-кабель).
- Перезатухающий
- Если s — пара действительных значений, то решение представляет собой просто сумму двух затухающих экспонент без колебаний. Этот случай имеет место для и называется перезатухающим . Ситуации, в которых избыточное демпфирование практично, обычно имеют трагические последствия, если происходит перерегулирование, обычно электрическое, а не механическое. Например, посадка самолета на автопилоте: если система промахнется и выпустит шасси слишком поздно, результатом будет катастрофа.
- Критически демпфированный
- Случай, когда является границей между случаями передемпфирования и недостаточного демпфирования и называется критически демпфированным . Это оказывается желательным результатом во многих случаях, когда требуется инженерное проектирование затухающего генератора (например, механизма закрытия двери).
Добротность и скорость затухания
[ редактировать ]Добротность , что , коэффициент затухания ζ и скорость экспоненциального затухания α связаны так [9]
Когда система второго порядка имеет (то есть, когда система недостаточно демпфирована), она имеет два комплексно-сопряженных полюса, каждый из которых имеет действительную часть ; то есть параметр скорости затухания представляет собой скорость экспоненциального затухания колебаний. Более низкий коэффициент демпфирования подразумевает меньшую скорость затухания, и поэтому очень недостаточно затухающие системы колеблются в течение длительного времени. [10] Например, высококачественный камертон , имеющий очень низкий коэффициент демпфирования, имеет длительные колебания, очень медленно затухающие после удара молотком.
Логарифмический декремент
[ редактировать ]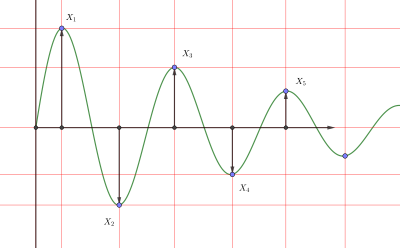
Для недостаточно демпфированных вибраций коэффициент демпфирования также связан с логарифмическим декрементом . Коэффициент затухания можно найти для любых двух пиков, даже если они не являются соседними. [11] Для соседних вершин: [12]
- где
где x 0 и x 1 — амплитуды любых двух последовательных пиков.
Как показано на правом рисунке:
где , – амплитуды двух последовательных положительных пиков и , – амплитуды двух последовательных отрицательных пиков.
Процентное превышение
[ редактировать ]В управления теории перерегулирование относится к выходному сигналу, превышающему его конечное, установившееся значение. [13] Для пошагового входа процентное перерегулирование (PO) представляет собой максимальное значение минус значение шага, разделенное на значение шага. В случае единичного шага перерегулирование представляет собой просто максимальное значение переходной характеристики минус единица.
Процентное перерегулирование (PO) связано с коэффициентом демпфирования ( ζ ) следующим образом:
И наоборот, коэффициент демпфирования ( ζ ), который дает заданный процент перерегулирования, определяется следующим образом:
Примеры и приложения
[ редактировать ]Вязкое сопротивление
[ редактировать ]Когда объект падает в воздухе, единственной силой, препятствующей его свободному падению, является сопротивление воздуха. Объект, падающий через воду или масло, будет замедляться с большей скоростью, пока в конечном итоге не достигнет установившейся скорости, поскольку сила сопротивления приходит в равновесие с силой гравитации. Это концепция вязкого сопротивления , которая, например, применяется в автоматических дверях или дверях с защитой от захлопывания. [14]
Демпфирование в электрических системах
[ редактировать ]Электрические системы, работающие с переменным током (AC), используют резисторы для гашения электрического тока, поскольку они являются периодическими. Диммеры или ручки громкости являются примерами демпфирования в электрической системе. [14]
Магнитное демпфирование и магнитореологическое демпфирование.
[ редактировать ]Кинетическая энергия, вызывающая колебания, рассеивается в виде тепла электрическими вихревыми токами , которые индуцируются при прохождении через полюса магнита, либо через катушку, либо через алюминиевую пластину. Вихревые токи являются ключевым компонентом электромагнитной индукции , поскольку они создают магнитный поток, прямо противодействующий колебательному движению, создавая силу сопротивления. [15] Другими словами, сопротивление, вызванное магнитными силами, замедляет систему. Примером применения этой концепции являются тормоза на американских горках. [16]
В магнитореологических демпферах (MR Dampers) используется магнитореологическая жидкость , вязкость которой изменяется под воздействием магнитного поля. В этом случае магнитореологическое демпфирование можно рассматривать как междисциплинарную форму демпфирования как с вязкостным, так и с магнитным механизмами демпфирования. [17] [18]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Эскюдье, Марсель; Аткинс, Тони (2019). «Словарь машиностроения» . Оксфордский справочник . doi : 10.1093/acref/9780198832102.001.0001 .
- ^ Стейдель (1971). Введение в механические вибрации . Джон Уайли и сыновья. п. 37.
затухающий — термин, используемый при изучении вибрации для обозначения рассеяния энергии.
- ^ Крэндалл, Ш. (январь 1970 г.). «Роль демпфирования в теории вибрации». Журнал звука и вибрации . 11 (1): 3–18, ИН1. дои : 10.1016/s0022-460x(70)80105-5 .
- ^ Дж. П. Мейяард; Дж. М. Пападопулос; А. Руина и А.Л. Шваб (2007). «Линеаризованные уравнения динамики баланса и рулевого управления велосипеда: ориентир и обзор». Труды Королевского общества А. 463 (2084): 1955–1982. Бибкод : 2007RSPSA.463.1955M . дои : 10.1098/rspa.2007.1857 . S2CID 18309860 .
возмущения наклона и рулевого управления угасают, казалось бы, затухая. Однако система не имеет истинного демпфирования и сохраняет энергию. Энергия колебаний наклона и поворота передается на скорость движения вперед, а не рассеивается.
- ^ Уроне, Пол Питер; Хинрикс, Роджер (2016). «16.7 Затухающее гармоническое движение» . Колледж физики . OpenStax – через Университет Центральной Флориды.
- ^ Дуглас К. Джанколи (2000). [ Физика для ученых и инженеров с современной физикой (3-е издание) ]. Прентис Холл. п. 387 ISBN 0-13-021517-1
- ^ Альсиаторе, Дэвид Г. (2007). Введение в мехатронику и измерения (3-е изд.). МакГроу Хилл. ISBN 978-0-07-296305-2 .
- ^ Рахман, Дж.; Муштак, М.; Али, А.; Анджам, Ю.Н.; Назир, С. (2014). «Моделирование системы демпфируемых массовых пружин в MATHLAB Simulink» . Журнал инженерно-технологического факультета . 2 .
- ^ Уильям МакКи. Зиберт. Цепи, сигналы и системы . МТИ Пресс.
- ^ Мин Рао и Хаймин Цю (1993). Инженерия управления технологическими процессами: учебник для инженеров-химиков, механиков и электриков . ЦРК Пресс. п. 96. ИСБН 978-2-88124-628-9 .
- ^ «Динамика и вибрации: Примечания: Свободные затухающие вибрации» .
- ^ «Оценка демпфирования» . 19 октября 2015 г.
- ^ Куо, Бенджамин С. и Голнараги М.Ф. (2003). Системы автоматического управления (Восьмое изд.). Нью-Йорк: Уайли. п. §7.3 с. 236–237. ISBN 0-471-13476-7 .
- ^ Перейти обратно: а б «Демпфирование | Определение, типы и примеры» . Британская энциклопедия . Проверено 9 июня 2021 г.
- ^ Гупта, БР (2001). Основы электротехники, электроники и приборостроения . С. Чанд Лимитед. п. 338. ИСБН 9788121901031 .
- ^ «Вихревые токи и магнитное демпфирование | Физика» . Courses.lumenlearning.com . Проверено 9 июня 2021 г.
- ^ ЛИ, ДАГ-ЯНГ; УЭРЛИ, НОРМАН М. (июнь 2000 г.). «Квазистационарный анализ Гершеля-Балкли электро- и магнитореологических демпферов режима потока» . Электрореологические жидкости и магнитореологические суспензии . ВСЕМИРНАЯ НАУЧНАЯ: 579–586. дои : 10.1142/9789812793607_0066 . ISBN 978-981-02-4258-9 .
- ^ Саварези, Серджио М.; Пуссо-Вассаль, Шарль; Спельта, Криштиану; Сенаме, Оливер; Дугард, Люк (01 января 2010 г.), Саварези, Серхио М.; Пуссо-Вассаль, Шарль; Спельта, Криштиану; Сенаме, Оливер (ред.), «ГЛАВА 2 — Технологии и модели полуактивной подвески» , Проектирование полуактивной подвески для транспортных средств , Бостон: Баттерворт-Хейнеманн, стр. 15–39, номер документа : 10.1016/b978-0- 08-096678-6.00002-х , ISBN 978-0-08-096678-6 , получено 15 июля 2023 г.
- « Демпфирование ». Британская энциклопедия .
- OpenStax, Колледж. « Физика ». Люмен .













































