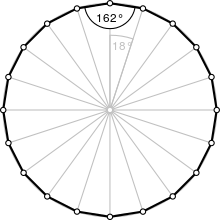
Икосагон

Правильный икосагон
Правильный икосагон
	Обычный икосагон
Тип	Правильный многоугольник
Ребра и вершины	20
Символ Шлефли	{20}, т{10}, тт{5}
Диаграммы Кокстера – Динкина	;
Группа симметрии	Двугранник (Д 20 ), заказ 2х20
Внутренний угол ( градусы )	162°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии икосагон или 20-угольник — это двадцатисторонний многоугольник . Сумма внутренних углов любого икосагона равна 3240 градусов.

Правильный икосагон

Правильный усеченный икосагон имеет Шлефли ${20}$ , а также может быть построен как t десятиугольник {10} $символ$ или дважды усеченный пятиугольник {5} $tt$ .

Один внутренний угол правильного икосагона равен 162°, а это означает, что один внешний угол будет равен 18°.

Площадь равна правильного икосагона с длиной $t$ ребра

A={5}t^{2}(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}})\simeq 31.5687t^{2}.

С точки зрения радиуса $R$ описанной окружности площадь равна

A={\frac {5R^{2}}{2}}({\sqrt {5}}-1);

так как площадь круга $\pi R^{2},$ правильный икосагон заполняет примерно 98,36% описанной окружности.

Использование

Большое колесо из популярного в США телевикторины The Price Is Right имеет икосагональное поперечное сечение.

Когда в 1989 году были проведены частичные раскопки, выяснилось, что «Глобус», театр под открытым небом, использовавшийся актерской труппой Уильяма Шекспира, был построен на икосагональном фундаменте. ^[1]

В качестве голигональной траектории свастика считается неправильным икосагоном. ^[2]

Правильный квадрат, пятиугольник и икосагон могут полностью заполнить вершину плоскости .

Строительство

Поскольку $20 = 2 2 \times 5$ правильный икосагон можно построить с помощью циркуля и линейки или путем разделения ребра пополам правильного десятиугольника или дважды разделенного пополам правильного пятиугольника :

Построение правильного икосагона	Построение правильного десятиугольника

Золотое сечение в икосагоне

В конструкции с заданной длиной стороны дуга вокруг $C$ радиусом $CD$ делит отрезок $E 20 F$ в соотношении золотого сечения.

{\frac {\overline {E_{20}E_{1}}}{\overline {E_{1}F}}}={\frac {\overline {E_{20}F}}{\overline {E_{20}E_{1}}}}={\frac {1+{\sqrt {5}}}{2}}=\varphi \approx 1.618

Симметрия

Правильный икосагон имеет $Dih 20$ симметрию порядка 40. Существует 5 диэдральных симметрий подгрупп: $(Dih 10, Dih 5)$ и $(Dih 4, Dih 2 и Dih 1)$ и 6 циклических групповых симметрий: $(Z 20, Z 10, Z 5)$ и ( $Z 4, Z 2, Z 1)$ .

Эти 10 симметрий можно увидеть в 16 различных симметриях на икосагоне, большем количестве, потому что линии отражения могут проходить либо через вершины, либо через края. Джон Конвей маркирует их буквенным и групповым порядком. ^[3] Полная симметрия правильной формы равна $r40$ , а отсутствие симметрии отмечено $a1$ . Двугранные симметрии делятся в зависимости от того, проходят ли они через вершины ( $d$ для диагонали) или ребра ( $p$ для перпендикуляров), и $i$ , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены буквой $g$ в соответствии с их центральными порядками вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только $подгруппа g20$ не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Неправильные икосагоны с наивысшей симметрией - это $d20$ , изогональный икосагон, построенный из десяти зеркал, которые могут чередовать длинные и короткие края, и $p20$ , изотоксальный икосагон, построенный с равными длинами ребер, но вершины чередуются с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного икосагона.

Диссекция

20-угольник со 180 ромбами
обычный	изотоксал

Коксетер утверждает, что каждый зоногон ( $2- метровый$ угольник, противоположные стороны которого параллельны и одинаковой длины) можно разрезать на $m (m -1)/2$ параллелограмма. ^[4]В частности, это верно для правильных многоугольников с четным числом сторон, и в этом случае все параллелограммы являются ромбами. Для икосагона $m =10$ , и его можно разделить на 45: 5 квадратов и 4 набора по 10 ромбов. Это разложение основано на Петри многоугольной проекции 10-куба с 45 из 11520 граней. В списке OEIS : A006245 указано количество решений как 18 410 581 880, включая до 20-кратных вращений и киральные формы в отражении.

Рассечение на 45 ромбов.
10-кубовый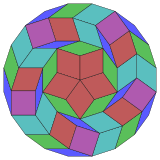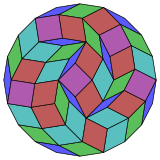

Связанные полигоны

Икосаграмма , — это 20-сторонний звездчатый многоугольник обозначенный символом ${20/n}$ . имеют три регулярные формы Символы Шлефли : ${20/3}$ , ${20/7}$ и ${20/9}$ . Есть также пять обычных звездных фигур (составных фигур), использующих такое же расположение вершин : $2{10}$ , $4{5}$ , $5{4}$ , $2{10/3}$ , $4{5/2}$ и $10{2}.$ .

н	1	2	3	4	5
Форма	Выпуклый многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{20/1} = {20}	{20/2} = 2{10}	{20/3}	{20/4} = 4{5}	{20/5} = 5{4}
Внутренний угол	162°	144°	126°	108°	90°
н	6	7	8	9	10
Форма	Сложный	Звездный многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{20/6} = 2{10/3}	{20/7}	{20/8} = 4{5/2}	{20/9}	{20/10} = 10{2}
Внутренний угол	72°	54°	36°	18°	0°

Более глубокие усечения правильного десятиугольника и декаграммы могут привести к образованию изогональных ( вершинно-транзитивных ) промежуточных форм икосаграммы с одинаково расположенными вершинами и двумя длинами ребер. ^[5]

Правильную икосаграмму ${20/9}$ можно рассматривать как квазиусеченный десятиугольник $t{10/9}={20/9}$ . Аналогично декаграмма { 10/3 $}$ имеет квазиусечение $t{10/7}={20/7}$ , и, наконец, простое усечение декаграммы дает $t{10/3}={20/3}$ .

Икосаграммы как усечения правильных декагонов и декаграмм, {10}, {10/3}
Квазирегулярный					Квазирегулярный
т{10}={20}					т{10/9}={20/9}
т{10/3}={20/3}					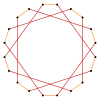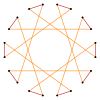т{10/7}={20/7}

Полигоны Петри

Правильный икосагон — это многоугольник Петри для ряда многогранников более высокой размерности, показанный в ортогональных проекциях на плоскости Кокстера :

А ₁₉	Б ₁₀		Д ₁₁	E₈	Ч ₄	⁠ 1 / 2 ⁠ 2H ₂	2H_2H2
19-симплекс	10-ортоплекс	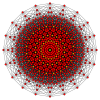10-кубовый	11-демикуб	(4 ₂₁)	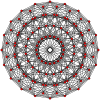600-ячеечный	Большая антипризма	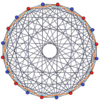10-10 дуопирамида	10-10 дуопризма

Это также многоугольник Петри для икосаэдра со 120 ячейками , малого звездчатого 120-ячеечного , большого икосаэдра со 120 ячейками и большого великого 120-ячеечного .

Ссылки

↑ Мюриэл Притчетт, Университет Джорджии, «To Span the Globe». Архивировано 10 июня 2010 г. в Wayback Machine , см. также примечание редактора, получено 10 января 2016 г.
^ Вайсштейн, Эрик В. «Икосагон» . Математический мир .
^ Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
^ Коксетер , Математические развлечения и очерки, тринадцатое издание, стр.141
^ Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории (1994), Метаморфозы многоугольников , Бранко Грюнбаум

Внешние ссылки

[1] Мюриэл Притчетт, Университет Джорджии, «To Span the Globe». Архивировано 10 июня 2010 г. в Wayback Machine , см. также примечание редактора, получено 10 января 2016 г.

[2] Вайсштейн, Эрик В. «Икосагон» . Математический мир .

[3] Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)

[4] Коксетер , Математические развлечения и очерки, тринадцатое издание, стр.141

[5] Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории (1994), Метаморфозы многоугольников , Бранко Грюнбаум

[1]

[2]

[3]

[4]

[5]