Выпрямленные 5-симплексы

Ортогональные проекции в _{A 5} плоскости Кокстера
5-симплекс	Выпрямленный 5-симплекс	Биректифицированный 5-симплекс

В пятимерной геометрии выпрямленный 5-симплекс — это выпуклый однородный 5-многогранник , являющийся выпрямлением правильного 5-симплекса .

Существует три уникальные степени ректификации, включая нулевую, собственно 5-симплекс. Вершины выпрямленного 5-симплекса расположены в центрах ребер 5-симплекса . Вершины биректифицированного 5-симплекса расположены в центрах треугольных граней 5-симплекса .

Выпрямленный 5-симплекс

Выпрямленный 5-симплекс Выпрямленный гексатерон (rix)
Тип	однородный 5-многогранник
Символ Шлефли	г{3 ⁴} или $\left\{{\begin{array}{l}3,3,3\\3\end{array}}\right\}$
Диаграмма Кокстера	или
4-ликий	12	6 {3,3,3} 6р {3,3,3}
Клетки	45	15 {3,3} 30р {3,3}
Лица	80	80 {3}
Края	60
Вершины	15
Вершинная фигура	{}×{3,3}
Группа Коксетера	А ₅ , [3 ⁴], порядок 720
Двойной
Базовая точка	(0,0,0,0,1,1)
Окружность	0.645497
Характеристики	выпуклый , изогональный изотоксальный

В пятимерной геометрии выпрямленный 5-симплекс — это однородный 5-многогранник с 15 вершинами , 60 ребрами , 80 треугольными гранями , 45 ячейками (30 тетраэдрическими и 15 октаэдрическими ) и 12 4-гранями (6 5-клеточными и 15 октаэдрическими). 6 выпрямленных 5-клеток ). Его также называют 0 _3,1 из-за его ветвящейся диаграммы Кокстера-Дынкина, показанной как .

Э. Л. Эльте определила его в 1912 году как полуправильный многогранник, обозначив его как S. ¹
₅.

Альтернативные названия

Выпрямленный гексатерон (аббревиатура: рикс) (Джонатан Бауэрс)

Координаты

Вершины выпрямленного 5-симплекса проще расположить на гиперплоскости в 6-мерном пространстве как перестановки (0,0,0,0,1,1) или (0,0,1,1,1,1). . Эти конструкции можно рассматривать как грани выпрямленного 6-ортоплекса или биректифицированного 6-куба соответственно.

В качестве конфигурации

Эта матрица конфигурации представляет собой выпрямленный 5-симплекс. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам и 4-граням. Диагональные числа говорят, сколько каждого элемента встречается во всем выпрямленном 5-симплексе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. ^[1]^[2]

Диагональные числа f-вектора получаются с помощью конструкции Витхоффа , разделяющей полный групповой порядок на подгруппу путем удаления одного зеркала за раз. ^[3]

A_А5	k-лицо	ж _к	ж ₀	ж ₁	f_f2		f ₃		ж ₄		к -фигура	примечания
А ₃ А ₁	( )	ж ₀	15	8	4	12	6	8	4	2	{3,3}×{ }	А ₅ /А ₃ А ₁ = 6!/4!/2 = 15
А ₂ А ₁	{ }	ж ₁	2	60	1	3	3	3	3	1	{3}∨( )	А ₅ /А ₂ А ₁ = 6!/3!/2 = 60
А ₂ А ₂	г{3}	f_f2	3	3	20	*	3	0	3	0	{3}	А ₅ /А ₂ А ₂ = 6!/3!/3! =20
А ₂ А ₁	{3}	f_f2	3	3	*	60	1	2	2	1	{ }×( )	А ₅ /А ₂ А ₁ = 6!/3!/2 = 60
А ₃ А ₁	г{3,3}	f ₃	6	12	4	4	15	*	2	0	{ }	А ₅ /А ₃ А ₁ = 6!/4!/2 = 15
A_А3	{3,3}	f ₃	4	6	0	4	*	30	1	1	{ }	А ₅ /А ₃ = 6!/4! = 30
A ₄	г {3,3,3}	ж ₄	10	30	10	20	5	5	6	*	( )	А ₅ /А ₄ = 6!/5! = 6
A ₄	{3,3,3}	ж ₄	5	10	0	10	0	5	*	6	( )	А ₅ /А ₄ = 6!/5! = 6

Изображения

Стереографическая проекция
Стереографическая проекция сферической формы.

орфографические проекции
К Самолет Коксетера	A_А5	A ₄
График
Двугранная симметрия	[6]	[5]
К Самолет Коксетера	A_А3	A_А2
График
Двугранная симметрия	[4]	[3]

Связанные многогранники

Выпрямленный 5-симплекс 0 ₃₁ является вторым в размерной серии однородных многогранников, выраженной Коксетером как 1 _3k серия. Пятая фигура — это евклидовы соты 3 ₃₁ , а последняя — некомпактные гиперболические соты 4 ₃₁ . Каждый прогрессивный однородный многогранник строится из предыдущего как его вершинная фигура .

k ₃₁ размерная фигура
н	4	5	6	7	8	9
Коксетер группа	А ₃ А ₁	A_А5	Д ₆	E ₇	${\tilde {E}}_{7}$ = E ₇⁺	${\bar {T}}_{8}$ =E ₇⁺⁺
Коксетер диаграмма
Симметрия	[3 ^−1,3,1]	[3 ^0,3,1]	[3 ^1,3,1]	[3 ^2,3,1]	[3 ^3,3,1]	[3 ^4,3,1]
Заказ	48	720	23,040	2,903,040	∞
График					-	-
Имя	−1 ₃₁	0 ₃₁	1 ₃₁	2 ₃₁	3 ₃₁	4 ₃₁

Биректифицированный 5-симплекс

Биректифицированный 5-симплекс Биректифицированный гексатерон (точка)
Тип	однородный 5-многогранник
Символ Шлефли	2р{3 ⁴} = {3 ^2,2} или $\left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}$
Диаграмма Кокстера	или
4-ликий	12	12 р{3,3,3}
Клетки	60	30 {3,3} 30р {3,3}
Лица	120	120 {3}
Края	90
Вершины	20
Вершинная фигура	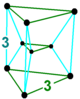{3}×{3}
Группа Коксетера	A ₅×2, [[3 ⁴]], порядок 1440
Двойной
Базовая точка	(0,0,0,1,1,1)
Окружность	0.866025
Характеристики	выпуклый , изогональный изотоксальный

Биректифицированный 5-симплекс изотопен выпрямленные 5 - , все 12 его граней представляют собой ячейки . Он имеет 20 вершин , 90 ребер , 120 треугольных граней , 60 ячеек (30 тетраэдрических и 30 октаэдрических ).

Э. Л. Эльте определила его в 1912 году как полуправильный многогранник, обозначив его как S. ²
₅.

Его также называют 0 _2,2 из-за его ветвящейся диаграммы Кокстера-Дынкина, показанной как . Это видно на вершинной фигуре 6-мерного 1 ₂₂ , .

Альтернативные названия

Биректифицированный гексатерон
додекатерон (аббревиатура: точка) (для 12-гранного политерона) (Джонатан Бауэрс)

Строительство

Элементы правильных многогранников можно выразить в виде матрицы конфигурации . Строки и столбцы ссылаются на вершины, ребра, грани и ячейки, а диагональные элементы — на их счетчики ( f-векторы ). Недиагональные элементы представляют количество элементов строки, инцидентных элементу столбца. ^[4]^[5]

Диагональные числа f-вектора получаются с помощью конструкции Витхоффа , разделяющей полный групповой порядок на подгруппу путем удаления одного зеркала за раз. ^[6]

A_А5	k-лицо	ж _к	ж ₀	ж ₁	f_f2		f ₃			ж ₄		к -фигура	примечания
А ₂ А ₂	( )	ж ₀	20	9	9	9	3	9	3	3	3	{3}×{3}	А ₅ /А ₂ А ₂ = 6!/3!/3! = 20
А ₁ А ₁ А ₁	{ }	ж ₁	2	90	2	2	1	4	1	2	2	{ }∨{ }	А ₅ /А ₁ А ₁ А ₁ = 6!/2/2/2 = 90
А ₂ А ₁	{3}	f_f2	3	3	60	*	1	2	0	2	1	{ }∨( )	А ₅ /А ₂ А ₁ = 6!/3!/2 = 60
А ₂ А ₁	{3}	f_f2	3	3	*	60	0	2	1	1	2	{ }∨( )	А ₅ /А ₂ А ₁ = 6!/3!/2 = 60
А ₃ А ₁	{3,3}	f ₃	4	6	4	0	15	*	*	2	0	{ }	А ₅ /А ₃ А ₁ = 6!/4!/2 = 15
A_А3	г{3,3}		6	12	4	4	*	30	*	1	1		А ₅ /А ₃ = 6!/4! = 30
А ₃ А ₁	{3,3}		4	6	0	4	*	*	15	0	2		А ₅ /А ₃ А ₁ = 6!/4!/2 = 15
A ₄	г {3,3,3}	ж ₄	10	30	20	10	5	5	0	6	*	( )	А ₅ /А ₄ = 6!/5! = 6
A ₄	г {3,3,3}	ж ₄	10	30	10	20	0	5	5	*	6	( )	А ₅ /А ₄ = 6!/5! = 6

Изображения

Проекция А5 имеет внешний вид, идентичный Кубу Метатрона . ^[7]

орфографические проекции
К Самолет Коксетера	A_А5	A ₄
График
Двугранная симметрия	[6]	[[5]]=[10]
К Самолет Коксетера	A_А3	A_А2
График
Двугранная симметрия	[4]	[[3]]=[6]

Пересечение двух 5-симплексов

Стереографическая проекция

Биректифицированный 5-симплекс представляет собой пересечение двух правильных 5-симплексов в дуальной конфигурации. Вершины биректификации существуют в центре граней исходного многогранника (ов). Это пересечение аналогично трехмерному звездчатому октаэдру , рассматриваемому как соединение двух правильных тетраэдров , пересекающихся в центральном октаэдре , при этом это первое выпрямление, при котором вершины находятся в центре исходных ребер.


Двойные 5-симплексы (красный и синий) и их биректифицированное 5-симплексное пересечение показаны зеленым цветом, если смотреть на плоскостях Кокстера A5 и A4. Симплексы перекрываются в проекции А5 и нарисованы пурпурным цветом.

Это также пересечение 6-куба с гиперплоскостью, которая перпендикулярно делит длинную диагональ 6-куба пополам. В этом смысле это 5-мерный аналог правильного шестиугольника, октаэдра и усеченной 5-клетки . Эта характеристика дает простые координаты вершин биректифицированного 5-симплекса в 6-мерном пространстве: 20 различных перестановок (1,1,1,−1,−1,−1).

Вершины биректифицированного 5-симплекса также можно расположить на гиперплоскости в 6-мерном пространстве как перестановки (0,0,0,1,1,1). Эту конструкцию можно рассматривать как грани биректифицированного 6-ортоплекса .

Связанные многогранники

k_22 многогранников

Биректифицированный 5-симплекс 0 ₂₂ является вторым в размерной серии однородных многогранников, выраженной Коксетером как серия k ₂₂ . Биректифицированный 5-симплекс является вершиной третьего числа, 1 ₂₂ . Четвертая фигура — это евклидовы соты 2 ₂₂ , а последняя — некомпактные гиперболические соты 3 ₂₂ . Каждый прогрессивный однородный многогранник строится из предыдущего как его вершинная фигура .

k ₂₂ фигуры в n измерениях
Космос	Конечный			евклидов	гиперболический
н	4	5	6	7	8
Коксетер группа	А ₂ А ₂	E_Е6	${\tilde {E}}_{6}$ = Е ₆⁺	${\bar {T}}_{7}$ = Е ₆⁺⁺
Коксетер диаграмма
Симметрия	[[3 ^2,2,-1]]	[[3 ^2,2,0]]	[[3 ^2,2,1]]	[[3 ^2,2,2]]	[[3 ^2,2,3]]
Заказ	72	1440	103,680	∞
График				∞	∞
Имя	−1 ₂₂	0 ₂₂	1 ₂₂	2 ₂₂	3 ₂₂

Многогранники изотопов

Изотопные однородные усеченные симплексы
Дим.	2	3	4	5	6	7	8
Имя Коксетер	Шестиугольник = т{3} = {6}	Октаэдр = г{3,3} = {3 ^1,1} = {3,4} $\left\{{\begin{array}{l}3\\3\end{array}}\right\}$	Десятилетия 2т{3 ³}	Додекатерон 2р{3 ⁴} = {3 ^2,2} $\left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}$	Тетрадекапетон 3т{3 ⁵}	Гексадекаэксон 3р{3 ⁶} = {3 ^3,3} $\left\{{\begin{array}{l}3,3,3\\3,3,3\end{array}}\right\}$	Октадеказеттон 4т{3 ⁷}
Изображения
Вершинная фигура	( )∨( )	{ }×{ }	{ }∨{ }	{3}×{3}	{3}∨{3}	{3,3}×{3,3}	{3,3}∨{3,3}
Фасеты		{3}	т{3,3}	г {3,3,3}	2т{3,3,3,3}	2р{3,3,3,3,3}	3т{3,3,3,3,3,3}
Как пересекающийся двойной симплексы	∩	∩	∩	∩	∩	∩	∩

Связанные однородные 5-многогранники

Этот многогранник является вершинной фигурой 6 -демикуба и рёберной фигурой однородного 2 ₃₁ многогранника .

Это также один из 19 однородных политеров, основанных на группе Кокстера [3,3,3,3] , все они показаны здесь в _{A 5} плоскости Кокстера ортогональных проекциях . (Вершины окрашены в порядке перекрытия проекций: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый с увеличением количества вершин)

Многогранники А5
t₀	t₁	t₂	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_0,4	t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4
t_0,2,4	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,1,2,3,4

Ссылки

^ Коксетер, Правильные многогранники, раздел 1.8. Конфигурации.
^ Коксетер, Комплексные правильные многогранники, стр.117
^ Клитцинг, Ричард. "o3x3o3o3o - рикс" .
^ Коксетер, Правильные многогранники, раздел 1.8. Конфигурации.
^ Коксетер, Комплексные правильные многогранники, стр.117
^ Клитцинг, Ричард. "o3o3x3o3o - точка" .
^ Мелхиседек, Друнвало (1999). Древняя тайна цветка жизни . Том. 1. Издательство светотехники. стр.160 Рисунок 6-12

ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  - (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  - (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
Клитцинг, Ричард. «5D однородные многогранники (политеры)» . o3x3o3o3o - рикс, o3o3x3o3o - точка

Внешние ссылки

Глоссарий по гиперпространству , Георгий Ольшевский.
Многогранники различных размерностей , Джонатан Бауэрс
- Ректифицированная униформа политера (Рикс), Джонатан Бауэрс
Многомерный глоссарий

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Коксетер, Правильные многогранники, раздел 1.8. Конфигурации.

[2] Коксетер, Комплексные правильные многогранники, стр.117

[3] Клитцинг, Ричард. "o3x3o3o3o - рикс" .

[4] Коксетер, Правильные многогранники, раздел 1.8. Конфигурации.

[5] Коксетер, Комплексные правильные многогранники, стр.117

[6] Клитцинг, Ричард. "o3o3x3o3o - точка" .

[7] Мелхиседек, Друнвало (1999). Древняя тайна цветка жизни . Том. 1. Издательство светотехники. стр.160 Рисунок 6-12

[1]

[2]

[3]

[4]

[5]

[6]

[7]