Ли Йе (математик)
Ли Е ( китайский : Ли Е ; Уэйд-Джайлз : Ли Йе ; 1192–1279), урожденный Ли Чжи (китайский: 李智 ), любезное имя Ли Цзинчжай (китайский: 李京之 ), [1] [2] китайский математик, политик и писатель, опубликовавший и усовершенствовавший метод Тянь Юань Шу для решения полиномиальных уравнений одной переменной. [1] [3] [4] [5] [6] [7] Вместе с китайским астрономом IV века Юй Си Ли Е предложил идею сферической Земли вместо плоской до достижений европейской науки в 17 веке.
Имя
[ редактировать ]Ли Е родился Ли Чжи, но позже изменил свое имя на Ли Е, чтобы избежать путаницы с третьим императором Тан , которого также звали Ли Чжи, удалив одну черту из своего первоначального имени, чтобы изменить характер. Его имя также иногда пишут как Ли Чжи или Ли Йе. Его литературное имя было Жэньцин ( китайский : 仁卿 ; Уэйд-Джайлс : Джен-ц'ин ), а его прозвище было Цзинчжай ( китайский : 敬斋 ; Уэйд-Джайлс : Цзин-чай ). [1] [2]
Жизнь
[ редактировать ]Ли Е родился в Дасине (ныне Пекин). Его отец был секретарем офицера чжурчжэньской армии . Ли сдал экзамен на государственную службу в 1230 году в возрасте 38 лет и был административным префектом префектуры Цзюнь в провинции Хэнань до монгольского вторжения в 1233 году . Тогда он жил в бедности в горной провинции Шаньси . В 1248 году он закончил свою самую известную работу «Цэюань хайцзин» ( 測圓海鏡 , «Морское зеркало круговых измерений »). [1] [8] Затем Ли вернулся в Хэбэй .
В 1257 году Хубилай-хан , внук Чингисхана , приказал Ли давать советы по науке. В 1259 году Ли завершил «Игу яньдуань» ( 益古演段 , «Новые шаги в вычислениях »), также учебник по математике. Став ханом , Хубилай дважды предлагал Ли правительственные должности, но Ли был слишком стар и болен здоровьем. В 1264 году Ли наконец принял должность в Академии Ханьлинь и стал писать официальные истории. Однако у него были политические последствия, и через несколько месяцев он ушел в отставку, снова сославшись на плохое здоровье. [1] Последние годы жизни он провел, преподавая в своем доме недалеко от горы Фэн Лунг в Юане, Хэбэй . Ли велел сыну сжечь все его книги, кроме « Морского зеркала круговых измерений» . [1]
Математика
[ редактировать ]Цюань Хайцзин
[ редактировать ]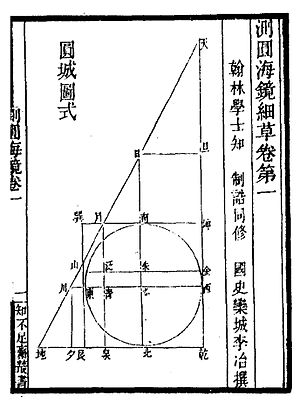
Цэюань хайцзин ( «Морское зеркало измерений круга ») представляет собой сборник из 170 задач, связанных с одним и тем же примером круглой городской стены, вписанной в прямоугольный треугольник и квадрат. [1] [9] В них часто участвуют два человека, которые идут по прямым линиям, пока не увидят друг друга, не встретятся или не доберутся до дерева в определенном месте. Целью книги было изучение сложных геометрических связей с алгеброй и поиск решений уравнений. [10]
Многие проблемы решаются с помощью полиномиальных уравнений, которые представлены с использованием метода, называемого Тянь Юань Шу , «метода массива коэффициентов» или буквально «метода небесного неизвестного». [1] [11] В той или иной форме этот метод был известен и до него. Это позиционная система стержневых цифр для обозначения полиномиальных уравнений .
Например, 2х 2 + 18x − 316 = 0 представляется как
元 . ( юань ) обозначает неизвестное x, поэтому цифры в этой строке означают 18x Строка ниже — это постоянный член (-316), а линия выше — коэффициент квадратичного (x 2 ) срок. Система учитывает произвольно высокие показатели неизвестного, добавляя больше строк сверху, и отрицательные показатели, добавляя строки под постоянным членом. Также могут быть представлены десятичные дроби. Позже порядок строк был изменен на обратный: первая строка имеет наименьший показатель степени.
Ли не объясняет, как вообще решать уравнения, а показывает это на примерах задач. Большинство уравнений можно свести ко второму, а иногда и к третьему порядку. Часто предполагается, что он использовал методы, аналогичные правилу Руффини и схеме Горнера .
Игу Яньдуань
[ редактировать ]
«Игу яньдуань» ( «Новые шаги в вычислениях ») — это работа по более фундаментальной математике, написанная вскоре после того, как Ли Е завершил Цейюань хайцзин, и, вероятно, была написана, чтобы помочь студентам, которые не могли понять Морское зеркало измерений круга . Игу яньдуань состоит из трех томов, посвященных решению геометрических задач на двух направлениях: через Тянь юань шу и геометрию. В нем также содержались алгебраические задачи, но с несколько другими обозначениями. [11]
Астрономия и форма Земли
[ редактировать ]Хунтянская предполагала , ( 渾天 ) теория небесной сферы что Земля плоская и квадратная , а небеса имеют сферическую форму, наряду с небесными телами, такими как Солнце и Луна (описанными ученым-эрудитом и государственным деятелем I века нашей эры Чжаном Хэн похож на арбалетную пулю и шар соответственно). [12] Однако идея плоской Земли подверглась критике со стороны астронома династии Цзинь Юй Си (307-345 гг. н. э.), который предложил в качестве альтернативы округлую форму. [13] В своей работе «Цзинчжай гу чжин чжу» ( «Древние и современные заметки Цзинчжай ») [14] Ли Е повторил идею Юя о том, что Земля имеет сферическую форму , похожую по форме на небо, но меньший по размеру, утверждая, что она не может быть квадратной, поскольку это будет препятствовать движению небес и небесных тел. [15]
Однако идея сферической Земли не была принята в основной китайской науке и картографии до 17 века, в период позднего Мин и раннего Цин , с появлением свидетельств европейского плавания . кругосветного [16] Теория плоской Земли в китайской науке была окончательно опровергнута в 17 веке. Иезуиты в Китае также представили сферическую модель Земли, выдвинутую древними греками, такими как Филолай и Эратосфен. [17] и представлен на картах мира, таких как Маттео Риччи » «Кунью Ванго Кванту , опубликованная в при династии Мин в 1602 году. Китае [18]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час Брерд, Андреа. (01 января 2021 г.). « Ли Е: китайский математик ». Британская энциклопедия . По состоянию на 7 февраля 2021 г.
- ↑ Перейти обратно: Перейти обратно: а б « Ли, Е (1192-1279)李,冶 (1192-1279) » IdRef: Идентификаторы и репозитории для высшего образования и исследований (на французском языке). По состоянию на 19 февраля 2018 г.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (декабрь 2003 г.). «Биография Ли Чжи» . MacTutor Архив истории математики . Университет Сент-Эндрюс в Шотландии . Проверено 21 декабря 2009 г.
- ^ Хо, Пэн Йок (2000). Ли, Ци и Шу: Введение в науку и цивилизацию в Китае (полное издание). Публикации Курьера Дувра. стр. 89–96. ISBN 0-486-41445-0 .
- ^ Хо, Пэн Йок (2008). «Ли Чжи, также называемый Ли Йе» . Полный словарь научной биографии . Сыновья Чарльза Скрибнера . Проверено 21 декабря 2009 г. Через энциклопедию.com.
- ^ Лам Лай-Ёнг; Анг Тянь-Се (сентябрь 1984 г.). «Ли Е и его И Гу Янь Дуань (старая математика в расширенных разделах)». Архив истории точных наук . 29 (3). Берлин / Гейдельберг: Springer: 237–266. дои : 10.1007/BF00348622 . S2CID 120593520 .
- ^ Светц, Фрэнк (1996). «Загадки китайской математики» . В Рональде Калинджере (ред.). Vita mathematica: исторические исследования и интеграция с преподаванием . Примечания МАА . Том. 40. Издательство Кембриджского университета. стр. 89–90. ISBN 0-88385-097-4 .
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , с. 40.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , стр. 44, 129.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , стр. 44–45.
- ↑ Перейти обратно: Перейти обратно: а б Нидэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , с. 45.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , стр. 216-218, 227.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , стр. 220, 498.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , с. 498; сноска И.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , с. 498.
- ^ Нидхэм, Джозеф; Ван, Линг. (1995) [1959]. Наука и цивилизация в Китае: Математика и науки о небе и Земле , том. 3, репринтное издание. Кембридж: Издательство Кембриджского университета. ISBN 0-521-05801-5 , стр. 498-499.
- ^ Каллен, Кристофер. (1993). «Приложение A: Китайский Эратосфен о плоской Земле: исследование фрагмента космологии в Хуайнаньцзы», майор, Джон. С. (редактор), Небо и Земля в ранней ханьской мысли: третья, четвертая и пятая главы Хуананьцзы . Олбани: Издательство Государственного университета Нью-Йорка. ISBN 0-7914-1585-6 , с. 269-270.
- ^ Баран, Мадлен (16 декабря 2009 г.). «Историческая карта приезжает в Миннесоту» . Сент-Пол, Миннесота: Общественное радио Миннесоты . Проверено 19 февраля 2018 г.
Дальнейшее чтение
[ редактировать ]- Чан, Хок-Лам. 1997. «Рецепт Кубилаю Каану по вопросам управления: случай Чан Дэ-хуэя и Ли Чжи». Журнал Королевского азиатского общества 7 (2). Издательство Кембриджского университета: 257–83. https://www.jstor.org/stable/25183352 .

