Семиугольник

Правильный семиугольник
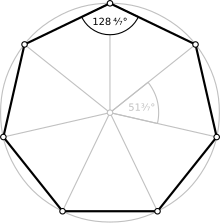Правильный семиугольник
Тип	Правильный многоугольник
Ребра и вершины	7
Символ Шлефли	{7}
Диаграммы Кокстера – Динкина
Группа симметрии	Dihedral (D 7 ), order 2×7
Внутренний угол ( градусы )	≈128.571°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии семиугольник — или семиугольник это семиугольник или 7-угольник.

Семиугольник иногда называют семиугольником , используя «септ-» ( исключение септуа- , латинского происхождения , числового префикса а не гепта- , числового префикса греческого происхождения; оба являются родственными) вместе с греческим суффиксом. «-agon» означает угол.

Правильный семиугольник

Правильный , у которого все стороны и все семиугольник углы равны, имеет внутренние углы 5π/7 радиан (128 4/7 ​ градусов ) . Его символ Шлефли — {7}.

Область

Площадь ( A ) правильного семиугольника со стороной a определяется выражением:

$A={\frac {7}{4}}a^{2}\cot {\frac {\pi }{7}}\simeq 3.634a^{2}.$

В этом можно убедиться, разделив семиугольник с единичной стороной на семь треугольных «кусков пирога» с вершинами в центре и вершинах семиугольника, а затем разделив каждый треугольник пополам, используя апофему в качестве общей стороны. Апофема равна котангенса половине $\pi /7,$ а площадь каждого из 14 маленьких треугольников составляет одну четвертую апофемы.

Площадь правильного семиугольника, вписанного в круг радиуса R, равна ${\tfrac {7R^{2}}{2}}\sin {\tfrac {2\pi }{7}},$ а площадь самого круга равна $\pi R^{2};$ таким образом, правильный семиугольник заполняет примерно 0,8710 описанной окружности.

Строительство

Поскольку 7 — простое число Пьерпона , но не простое число Ферма , правильный семиугольник невозможно построить с помощью циркуля и линейки , но можно построить с помощью помеченной линейки и циркуля. Это наименьший правильный многоугольник с таким свойством. Такая конструкция называется неусисной конструкцией . Его также можно построить с помощью циркуля, линейки и трисектора угла. Невозможность построения линейки и циркуля следует из наблюдения, что $\scriptstyle {2\cos {\tfrac {2\pi }{7}}\approx 1.247}$ является нулем неприводимой кубики x ³ + х ² - 2 Икс - 1 . Следовательно, этот многочлен является минимальным многочленом от 2cos( 2π ⁄ 7 ), тогда как степень минимального многочлена конструктивного числа должна быть степенью 2.

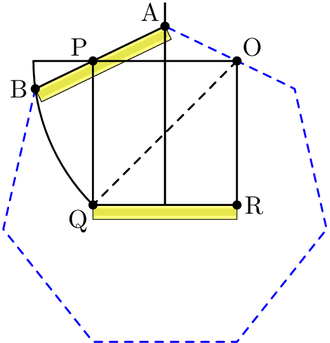Нейзисная конструкция внутреннего угла правильного семиугольника.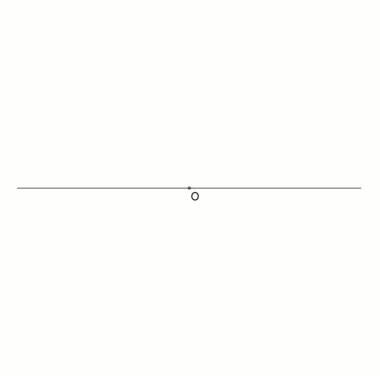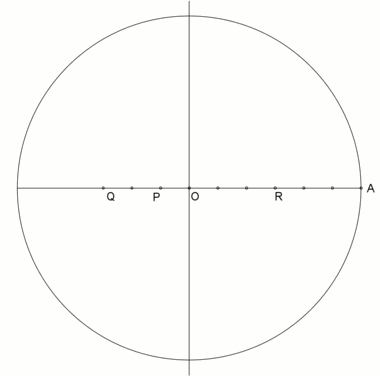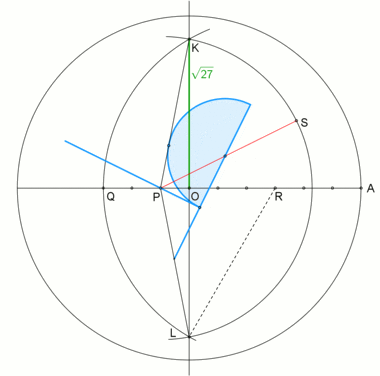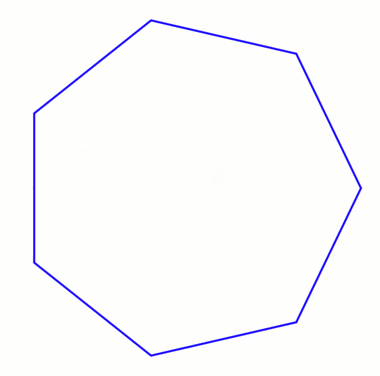

Анимация конструкции neusis с радиусом описанной окружности. ${\overline {OA}}=6$, по словам Эндрю М. Глисона на основе трисекции угла с помощью томагавка . Эта конструкция опирается на то, что $6\cos \left({\frac {2\pi }{7}}\right)=2{\sqrt {7}}\cos \left({\frac {1}{3}}\arctan \left(3{\sqrt {3}}\right)\right)-1.$

Семиугольник с заданной длиной стороны :
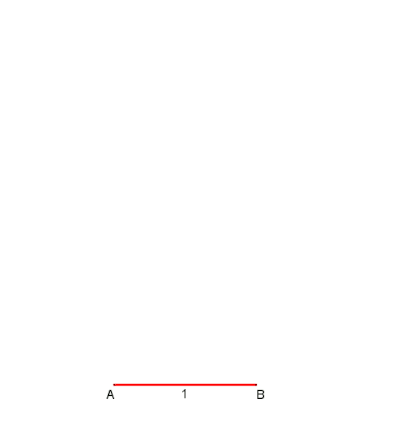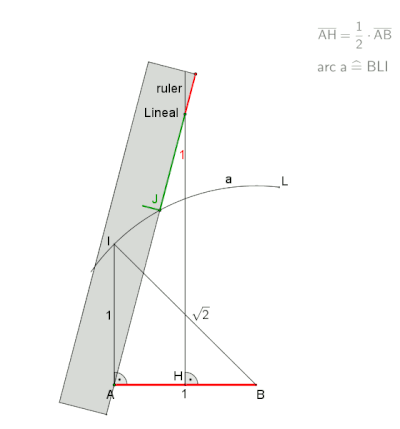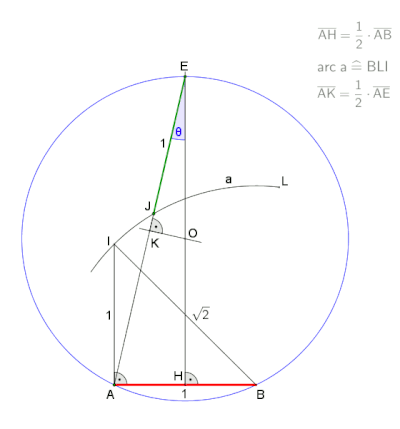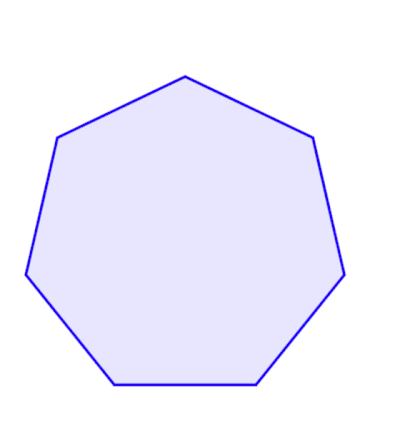
Анимация конструкции neusis с отмеченной линейкой, по словам Дэвида Джонсона Лейска ( Крокетт Джонсон ).

Приближение

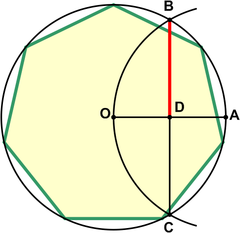
Приближением для практического использования с погрешностью около 0,2% является использование половины стороны равностороннего треугольника, вписанного в ту же окружность, что и длина стороны правильного семиугольника. Неизвестно, кто первым нашел это приближение, но оно было упомянуто Героном Александрийским в « Метрике» в I веке нашей эры, было хорошо известно средневековым исламским математикам, и его можно найти в работах Альбрехта Дюрера . Пусть А лежит на окружности описанной окружности. Нарисуйте дугу BOC . Затем $\scriptstyle {BD={1 \over 2}BC}$ дает приближение края семиугольника.

В этом приближении используется $\scriptstyle {{\sqrt {3}} \over 2}\approx 0.86603$ для стороны семиугольника, вписанного в единичный круг, а точное значение равно $\scriptstyle 2\sin {\pi \over 7}\approx 0.86777$.

Пример, иллюстрирующий ошибку:
При радиусе описанной окружности r = 1 м абсолютная погрешность 1-й стороны составит примерно -1,7 мм.

Другие приближения

Существуют и другие приближения семиугольника с использованием циркуля и линейки, но их рисование требует много времени.

Симметрия

Симметрии правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. Приказы о вращении даны в центре.

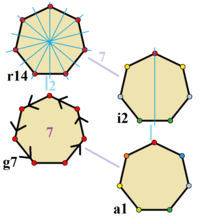
Правильный семиугольник принадлежит D _7h точечной группе ( обозначение Шенфлиса ), порядка 28. Элементами симметрии являются: ось собственного вращения 7-го порядка C ₇ , ось несобственного вращения 7-го порядка S ₇ , 7 вертикальных зеркальных плоскостей, σ _v , 7 осей 2-кратного вращения, C ₂ , в плоскости семиугольника и горизонтальной зеркальной плоскости σ _h , также в плоскости семиугольника.

Диагонали и семиугольный треугольник

Основная статья: Семиугольный треугольник

a = красная, b = синяя, c = зеленые линии

правильного семиугольника Сторона a , более короткая диагональ b и более длинная диагональ c с a < b < c удовлетворяют условиям

$a^{2}=c(c-b),$

$b^{2}=a(c+a),$

$c^{2}=b(a+b),$

${\frac {1}{a}}={\frac {1}{b}}+{\frac {1}{c}}$ ( оптическое уравнение )

и, следовательно,

$ab+ac=bc,$

и

$b^{3}+2b^{2}c-bc^{2}-c^{3}=0,$

$c^{3}-2c^{2}a-ca^{2}+a^{3}=0,$

$a^{3}-2a^{2}b-ab^{2}+b^{3}=0,$

Таким образом, b / c , c / a и a / b удовлетворяют кубическому уравнению. $t^{3}-2t^{2}-t+1=0.$ Однако для решений этого уравнения не существует алгебраических выражений с чисто вещественными членами, поскольку оно является примером неприводимого casus .

Приблизительные длины диагоналей в терминах стороны правильного семиугольника определяются выражением

$b\approx 1.80193\cdot a,\qquad c\approx 2.24698\cdot a.$

У нас также есть

$b^{2}-a^{2}=ac,$

$c^{2}-b^{2}=ab,$

$a^{2}-c^{2}=-bc,$

и

${\frac {b^{2}}{a^{2}}}+{\frac {c^{2}}{b^{2}}}+{\frac {a^{2}}{c^{2}}}=5.$

Семиугольный треугольник имеет вершины, совпадающие с первой, второй и четвертой вершинами правильного семиугольника (из произвольной начальной вершины), и углы $\pi /7,2\pi /7,$ и $4\pi /7.$ Таким образом, его стороны совпадают с одной стороной и двумя частными диагоналями правильного семиугольника.

В многогранниках

За исключением семиугольной призмы и семиугольной антипризмы , ни один выпуклый многогранник, полностью составленный из правильных многоугольников, не содержит семиугольника в качестве грани.

Звездные семиугольники

Два типа звездных семиугольников ( гептаграмм ) могут быть построены из правильных семиугольников, обозначенных символами Шлефли {7/2} и {7/3}, причем делителем является интервал соединения.

Синие, {7/2} и зеленые {7/3} звездные семиугольники внутри красного семиугольника.

Укладка плитки и упаковка

Треугольник, семиугольник и вершина из 42 угольников

Гиперболическая мозаика семиугольника

Правильный треугольник, семиугольник и 42-угольник могут полностью заполнить вершину плоскости . Однако мозаика плоскости только этими многоугольниками невозможна, поскольку невозможно поместить один из них на третью сторону треугольника, не оставляя зазора или не создавая перекрытия. В гиперболической плоскости возможны замощения правильными семиугольниками. На евклидовой плоскости также возможны вогнутые семиугольники.

Самая плотная двойная решетчатая упаковка евклидовой плоскости правильными семиугольниками, предположительно имеющая наименьшую максимальную плотность упаковки среди всех выпуклых множеств.

Правильный семиугольник имеет двойную решетчатую упаковку евклидовой плоскости с плотностью упаковки примерно 0,89269. Было высказано предположение, что это наименьшая возможная плотность для оптимальной плотности упаковки двойной решетки любого выпуклого множества и, в более общем плане, для оптимальной плотности упаковки любого выпуклого множества.

Эмпирические примеры

Семиугольник, разделенный на треугольники, глиняная табличка из Суз , 2-е тысячелетие до н.э.

Семиугольный купол мавзолея принца Эрнста

В Соединенном Королевстве с 1982 года выпускаются две семиугольные монеты : 50 пенсов и 20 пенсов. Барбадосский доллар также имеет семиугольную форму. Строго говоря, форма монет представляет собой семиугольник Рело , криволинейный семиугольник, имеющий кривые постоянной ширины ; боковые стороны изогнуты наружу, что позволяет монетам плавно катиться, когда они вставляются в торговый автомат . Монеты Ботсваны пула номиналом 2 пулы, 1 пула, 50 фив и 5 фив также имеют форму семиугольников с равносторонней кривизной. Монеты в форме семиугольников Рело также находятся в обращении на Маврикии, ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, Гаити, Ямайке, Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, острове Мэн, Гибралтар, Гайана, Соломоновы острова, Фолклендские острова и остров Святой Елены. Монета Замбии номиналом 1000 квач представляет собой настоящий семиугольник.

монете На бразильской достоинством 25 центов в диск вписан семиугольник. В некоторых старых вариантах герба Грузии , в том числе в советские времена , в качестве элемента использовалась гептаграмма {7/2}.

Ряд монет, в том числе монета в 20 евроцентов , имеют семиугольную симметрию в форме, называемой испанским цветком .

В архитектуре семиугольные планы этажей встречаются очень редко. Замечательным примером является Мавзолей принца Эрнста в Штадтхагене , Германия .

Многие значки полицейских в США имеют контур гептаграммы {7/2}.

См. также

• Гептаграмма
• Полигон

Внешние ссылки

• Определение и свойства семиугольника С интерактивной анимацией
• Семиугольник по Джонсону
• Еще один примерный метод строительства
• Многоугольники – Семиугольники
• Недавно открытое высокоточное приближение построения правильного семиугольника.
• Семиугольник, аппроксимирующая конструкция в виде анимации.
• Семиугольник с заданной стороной, аппроксимирующая конструкция в виде анимации.

Семиугольник