Комплексный анализ
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( Март 2021 г. ) |
| Математический анализ → Комплексный анализ |
| Комплексный анализ |
|---|
 |
| Комплексные числа |
| Сложные функции |
| Основная теория |
| Геометрическая теория функций |
| Люди |
Комплексный анализ , традиционно известный как теория функций комплексной переменной , является разделом математического анализа , который исследует функции комплексных чисел . Он полезен во многих разделах математики, включая алгебраическую геометрию , теорию чисел , аналитическую комбинаторику и прикладную математику , а также в физике , включая разделы гидродинамики , термодинамики , квантовой механики и твисторной теории . В более широком смысле, использование комплексного анализа также находит применение в инженерных областях, таких как ядерная , аэрокосмическая , машиностроительная и электротехника . [1]
Поскольку дифференцируемая функция комплексной переменной равна своему ряду Тейлора (то есть она аналитична ), комплексный анализ особенно касается аналитических функций комплексной переменной, то есть голоморфных функций . Эту концепцию можно распространить на функции нескольких комплексных переменных .
История [ править ]

Комплексный анализ — один из классических разделов математики, уходящий корнями в XVIII век и чуть раньше. Важные математики, связанные с комплексными числами, включают Эйлера , Гаусса , Римана , Коши , Гёста Миттаг-Леффлера , Вейерштрасса и многих других в 20 веке. Комплексный анализ, в частности теория конформных отображений , имеет множество физических приложений, а также используется во всей аналитической теории чисел . В наше время он стал очень популярен благодаря новому импульсу от сложной динамики и изображений фракталов, получаемых путем итерации голоморфных функций . Другое важное применение комплексного анализа находится в теории струн , которая исследует конформные инварианты квантовой теории поля .
Сложные функции [ править ]

Комплексная функция — это функция преобразования комплексных чисел в комплексные числа. Другими словами, это функция, которая имеет (не обязательно правильное) подмножество комплексных чисел в качестве домена и комплексных чисел в качестве кодомена . Обычно предполагается, что комплексные функции имеют область определения, содержащую непустое открытое подмножество комплексной плоскости .
Для любой сложной функции значения из домена и их изображений в диапазоне можно разделить на действительную и мнимую части:
где все они имеют реальную стоимость.
Другими словами, сложная функция может быть разложено на
- и
т. е. на две действительные функции ( , ) двух действительных переменных ( , ).
Аналогично, любую комплексную функцию f на произвольном множестве X ( изоморфную и, следовательно, в этом смысле) можно рассматривать как упорядоченную пару двух вещественных функций : (Re f , Im f ) или, альтернативно, как векторная функция из X в
Некоторые свойства комплекснозначных функций (например, непрерывность ) представляют собой не что иное, как соответствующие свойства векторнозначных функций двух действительных переменных. Другие понятия комплексного анализа, такие как дифференцируемость , являются прямыми обобщениями аналогичных понятий для действительных функций, но могут иметь совсем другие свойства. В частности, каждая дифференцируемая комплексная функция является аналитической (см. следующий раздел), а две дифференцируемые функции, равные в окрестности точки, равны на пересечении своей области определения (если области определения соединены ). Последнее свойство лежит в основе принципа аналитического продолжения , который позволяет расширить каждую действительную аналитическую функцию уникальным образом и получить комплексную аналитическую функцию, областью определения которой является вся комплексная плоскость с удаленным конечным числом дуг кривой . многие основные и специальные Таким образом определяются комплексные функции, включая комплексную показательную функцию , комплексные логарифмические функции и тригонометрические функции. .
Голоморфные функции [ править ]
Комплексные функции, дифференцируемые в каждой точке открытого подмножества. комплексной плоскости называются голоморфными на . В контексте комплексного анализа производная в определяется как [2]
На первый взгляд это определение формально аналогично определению производной вещественной функции. Однако комплексные производные и дифференцируемые функции ведут себя существенно иначе, чем их реальные аналоги. В частности, чтобы этот предел существовал, значение разностного отношения должно приближаться к одному и тому же комплексному числу, независимо от того, каким образом мы приближаемся к нему. в комплексной плоскости. Следовательно, комплексная дифференцируемость имеет гораздо более сильные последствия, чем реальная дифференцируемость. Например, голоморфные функции бесконечно дифференцируемы , тогда как существование n -й производной не обязательно влечет за собой существование ( n + 1)-й производной для вещественных функций. Более того, все голоморфные функции удовлетворяют более сильному условию аналитичности , что означает, что функция в каждой точке своей области локально задается сходящимся степенным рядом. По сути это означает, что функции, голоморфные на может быть сколь угодно хорошо аппроксимирована полиномами в некоторой окрестности каждой точки множества. . Это резко контрастирует с дифференцируемыми действительными функциями; существуют бесконечно дифференцируемые действительные функции, нигде не аналитические; см . Неаналитическая гладкая функция § Гладкая функция, которая нигде не является действительно аналитической .
Большинство элементарных функций, включая показательную функцию , тригонометрические функции и все полиномиальные функции , соответствующим образом расширяются до комплексных аргументов как функции. , голоморфны на всей комплексной плоскости, что делает их целыми функциями , а рациональные функции , где p и q — полиномы, голоморфны в областях, исключающих точки, где q равно нулю. Такие функции, голоморфные всюду, кроме множества изолированных точек, называются мероморфными функциями . С другой стороны, функции , , и не голоморфны нигде на комплексной плоскости, о чем свидетельствует их неудовлетворение условиям Коши–Римана (см. ниже).
Важным свойством голоморфных функций является связь между частными производными их вещественной и мнимой составляющих, известная как условия Коши–Римана . Если , определяемый , где , голоморфен в области , то для всех ,
С точки зрения действительной и мнимой частей функции u и v это эквивалентно паре уравнений и , где индексы указывают на частичное дифференцирование. Однако условия Коши–Римана не характеризуют голоморфные функции без дополнительных условий непрерывности (см. теорему Лумана–Меншоффа ).
Голоморфные функции обладают некоторыми замечательными особенностями. Например, теорема Пикара утверждает, что диапазон целой функции может принимать только три возможные формы: , , или для некоторых . Другими словами, если два различных комплексных числа и не находятся в диапазоне всей функции , затем является постоянной функцией. Более того, голоморфная функция на связном открытом множестве определяется ее ограничением на любое непустое открытое подмножество.
Конформная карта [ править ]

В математике конформное отображение — это функция , которая локально сохраняет углы , но не обязательно длины.
Более формально, пусть и быть открытыми подмножествами . Функция называется конформным (или сохраняющим угол) в точке если он сохраняет углы между направленными кривыми через , а также сохранение ориентации. Конформные карты сохраняют как углы, так и формы бесконечно малых фигур, но не обязательно их размер или кривизну .
Конформное свойство может быть описано в терминах Якобиана матрицы производных координатного преобразования . Преобразование является конформным, если якобиан в каждой точке представляет собой положительный скаляр, умноженный на матрицу вращения ( ортогональную определителю). Некоторые авторы определяют конформность как включающую в себя отображения, меняющие ориентацию, якобианы которых можно записать как любое скалярное произведение на любую ортогональную матрицу. [3]
Для двумерных отображений конформные отображения (сохраняющие ориентацию) представляют собой в точности локально обратимые комплексные аналитические функции. В трехмерных и более высоких измерениях теорема Лиувилля резко ограничивает конформные отображения несколькими типами.
Понятие конформности естественным образом обобщается на отображения между римановыми или полуримановыми многообразиями .Основные результаты
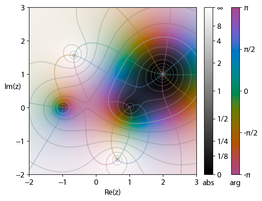
Оттенок представляет аргумент , яркость — величину.
Одним из центральных инструментов комплексного анализа является линейный интеграл . Линейный интеграл по замкнутому пути функции, голоморфной всюду внутри области, ограниченной замкнутым путем, всегда равен нулю, как утверждает интегральная теорема Коши . Значения такой голоморфной функции внутри диска можно вычислить с помощью интеграла по путям на границе диска (как показано в интегральной формуле Коши ). теория вычетов Интегралы по путям в комплексной плоскости часто используются для определения сложных действительных интегралов, и здесь среди прочих применима (см. методы контурного интегрирования ). «Полюс» (или изолированная особенность ) функции — это точка, в которой значение функции становится неограниченным или «взрывается». Если у функции есть такой полюс, то там можно вычислить остаток функции, который можно использовать для вычисления интегралов по путям, включающих функцию; это содержание мощной теоремы о вычетах . Замечательное поведение голоморфных функций вблизи существенных особенностей описывается формулой Теорема Пикара . Функции, имеющие только полюсы, но не имеющие существенных особенностей, называются мероморфными . Ряды Лорана являются комплекснозначным эквивалентом рядов Тейлора , но их можно использовать для изучения поведения функций вблизи особенностей с помощью бесконечных сумм более понятных функций, таких как полиномы.
Ограниченная функция , голоморфная во всей комплексной плоскости, должна быть постоянной; это теорема Лиувилля . Его можно использовать для естественного и краткого доказательства фундаментальной теоремы алгебры , которая утверждает, что поле комплексных чисел алгебраически замкнуто .
Если функция голоморфна во всей связной области, то ее значения полностью определяются ее значениями в любой меньшей подобласти. Говорят, что функция в большей области аналитически продолжается от своих значений в меньшей области. Это позволяет расширить определение функций, таких как дзета-функция Римана , которые изначально определяются в терминах бесконечных сумм, сходящихся только в ограниченных областях, почти на всю комплексную плоскость. Иногда, как в случае с натуральным логарифмом , невозможно аналитически продолжить голоморфную функцию до неодносвязной области на комплексной плоскости, но можно расширить ее до голоморфной функции на тесно связанной поверхности, известной как Риманова поверхность .
Все это относится к комплексному анализу по одной переменной. Существует также очень богатая теория комплексного анализа в более чем одном комплексном измерении , в которой сохраняются аналитические свойства, такие как разложение в степенной ряд , тогда как большинство геометрических свойств голоморфных функций в одном комплексном измерении (например, конформность ) не сохраняются. . Теорема Римана об отображении о конформных отношениях определенных областей на комплексной плоскости, которая может быть наиболее важным результатом одномерной теории, резко терпит неудачу в более высоких измерениях.
Основное применение некоторых комплексных пространств находится в квантовой механике в качестве волновых функций .
См. также [ править ]
- Сложная геометрия
- Гиперкомплексный анализ
- Векторное исчисление
- Список тем сложного анализа
- Теорема о монодромии
- Реальный анализ
- Теорема Римана – Роха
- Теорема Рунге
Ссылки [ править ]
- ^ «Промышленное применение комплексного анализа» . Ньютон «Ворота в математику» . 30 октября 2019 г. . Проверено 20 ноября 2023 г.
- ^ Рудин, Уолтер (1987). Реальный и комплексный анализ (PDF) . Макгроу-Хилл Образование. п. 197. ИСБН 978-0-07-054234-1 .
- ^ Блэр, Дэвид (17 августа 2000 г.). Теория инверсии и конформное отображение . Студенческая математическая библиотека. Том. 9. Провиденс, Род-Айленд: Американское математическое общество. дои : 10.1090/stml/009 . ISBN 978-0-8218-2636-2 . S2CID 118752074 .
Источники [ править ]
- Абловиц, М. Дж. и А. С. Фокас , Комплексные переменные: введение и применение (Кембридж, 2003).
- Альфорс Л. Комплексный анализ (McGraw-Hill, 1953).
- Х. Картан Элементарная теория аналитических функций одной или нескольких комплексных переменных. (Герман, 1961). Английский перевод, Элементарная теория аналитических функций одной или нескольких комплексных переменных. (Аддисон-Уэсли, 1963).
- Каратеодори, К. , Функционентеория. (Биркхойзер, 1950). Английский перевод, Теория функций комплексной переменной (Челси, 1954). [2 тома.]
- Кэрриер, Г.Ф. , М. Крук и К.Э. Пирсон, Функции комплексной переменной: теория и техника. (МакГроу-Хилл, 1966).
- Конвей, Дж. Б. , Функции одной комплексной переменной. (Спрингер, 1973).
- Фишер С. Комплексные переменные. (Уодсворт и Брукс/Коул, 1990).
- Форсайт А. Теория функций комплексной переменной (Кембридж, 1893).
- Фрайтаг, Э. и Р. Бусам, теория функций . (Спрингер, 1995). Английский перевод, Комплексный анализ . (Спрингер, 2005).
- Гурса Э. , Курс математического анализа, том 2 . (Готье-Виллар, 1905). Английский перевод, Курс математического анализа, вып. 2, часть 1: Функции комплексной переменной . (Гинн, 1916).
- Хенричи П. Прикладной и вычислительный комплексный анализ (Wiley). [Три тома: 1974, 1977, 1986 гг.]
- Крейциг, Э. , Высшая инженерная математика. (Уайли, 1962).
- Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. ( Methods of the Theory of Functions of a Complex Variable ). (1951, in Russian).
- Маркушевич А.И. , Теория функций комплексного переменного , (Прентис-Холл, 1965). [Три тома.]
- Марсден и Хоффман, Базовый комплексный анализ. (Фриман, 1973).
- Нидэм Т. Визуальный комплексный анализ. (Оксфорд, 1997). http://usf.usfca.edu/vca/
- Р. Реммерт Теория комплексных функций . (Спрингер, 1990).
- В. Рудин Реальный и комплексный анализ. (МакГроу-Хилл, 1966).
- Шоу, В.Т., Комплексный анализ с помощью Mathematica (Кембридж, 2006).
- Штейн, Э. и Р. Шакарчи, Комплексный анализ. (Принстон, 2003).
- Sveshnikov, A. G. & A. N. Tikhonov , Теория функций комплексной переменной. (Nauka, 1967). English translation, The Theory Of Functions Of A Complex Variable (MIR, 1978).
- Титчмарш, ЕС , Теория функций. (Оксфорд, 1932 г.).
- Вегерт Э. Визуальные сложные функции . (Биркхойзер, 2012).
- Уиттакер, Э.Т. и Дж.Н. Уотсон , Курс современного анализа . (Кембридж, 1902 г.). 3-е изд. (1920)





































