Взаимодействие Ферми

Не путать с контактным взаимодействием Ферми .

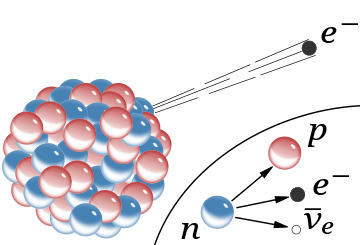
б ⁻
распад в атомном ядре (сопутствующее антинейтрино опущено). На вставке показан бета-распад свободного нейтрона. В обоих процессах промежуточная эмиссия виртуального
В ⁻
бозон (который затем распадается на электрон и антинейтрино) не показан.

В физике элементарных частиц взаимодействие Ферми (также теория бета-распада Ферми или Ферми четырехфермионное взаимодействие ) является объяснением бета-распада , предложенным Энрико Ферми в 1933 году. Теория постулирует, что четыре фермиона напрямую взаимодействуют друг с другом (в одной вершине соответствующей диаграммы Фейнмана ). Это взаимодействие объясняет бета-распад нейтрона прямым взаимодействием нейтрона с электроном , нейтрино (позже определенным как антинейтрино ) и протоном .

Ферми впервые представил эту связь в своем описании бета-распада в 1933 году. Ферми-взаимодействие было предшественником теории слабого взаимодействия , в которой взаимодействие между протоном-нейтроном и электроном-антинейтрино опосредовано виртуальным W ⁻ бозон , из которых теория Ферми является низкоэнергетической эффективной теорией поля .

По мнению Юджина Вигнера , который вместе с Джорданом ввёл преобразование Джордана-Вигнера , статья Ферми о бета-распаде стала его главным вкладом в историю физики.

История первоначального отклонения и более поздней публикации

Ферми впервые представил свою «предварительную» теорию бета-распада в престижный научный журнал Nature , который отверг ее, «поскольку она содержала предположения, слишком далекие от реальности, чтобы представлять интерес для читателя». Утверждалось, что Nature позже признала этот отказ одной из величайших редакционных ошибок в своей истории, но биограф Ферми Дэвид Н. Шварц возразил, что это недоказанно и маловероятно. Затем Ферми представил исправленные версии статьи в итальянские и немецкие издания, которые приняли и опубликовали их на этих языках в 1933 и 1934 годах. В то время статья не появилась в основной публикации на английском языке. Английский перевод основополагающей статьи был опубликован в Американском журнале физики в 1968 году.

Ферми настолько обеспокоил первоначальный отказ от статьи, что он решил на некоторое время отдохнуть от теоретической физики и заняться только экспериментальной физикой. Вскоре это привело к его знаменитой работе по активации ядер медленными нейтронами.

«Попытка»

Определения

Теория рассматривает три типа частиц, предположительно находящихся в прямом взаимодействии: первоначально « тяжелая частица » в «нейтронном состоянии» ( $\rho =+1$), который затем переходит в свое «протонное состояние» ( $\rho =-1$) с испусканием электрона и нейтрино.

Электронное состояние

$\psi =\sum _{s}\psi _{s}a_{s},$

где $\psi$ – одноэлектронная волновая функция , $\psi _{s}$ являются его стационарными состояниями .

$a_{s}$ — оператор, уничтожающий электрон в состоянии $s$ который действует в пространстве Фока как

$a_{s}\Psi (N_{1},N_{2},\ldots ,N_{s},\ldots )=(-1)^{N_{1}+N_{2}+\cdots +N_{s}-1}(1-N_{s})\Psi (N_{1},N_{2},\ldots ,1-N_{s},\ldots ).$

$a_{s}^{*}$ является оператором создания электронного состояния $s:$

$a_{s}^{*}\Psi (N_{1},N_{2},\ldots ,N_{s},\ldots )=(-1)^{N_{1}+N_{2}+\cdots +N_{s}-1}N_{s}\Psi (N_{1},N_{2},\ldots ,1-N_{s},\ldots ).$

Состояние нейтрино

Сходным образом,

$\phi =\sum _{\sigma }\phi _{\sigma }b_{\sigma },$

где $\phi$ — волновая функция одиночного нейтрино, а $\phi _{\sigma }$ являются его стационарными состояниями.

$b_{\sigma }$ — оператор, уничтожающий нейтрино в состоянии $\sigma$ который действует в пространстве Фока как

$b_{\sigma }\Phi (M_{1},M_{2},\ldots ,M_{\sigma },\ldots )=(-1)^{M_{1}+M_{2}+\cdots +M_{\sigma }-1}(1-M_{\sigma })\Phi (M_{1},M_{2},\ldots ,1-M_{\sigma },\ldots ).$

$b_{\sigma }^{*}$ является оператором создания состояния нейтрино $\sigma$.

Состояние тяжелых частиц

$\rho$ — это оператор, введенный Гейзенбергом (позже обобщенный в изоспин ), который действует на состояние тяжелой частицы , собственное значение которого имеет +1, когда частица является нейтроном, и -1, если частица является протоном. Поэтому состояния тяжелых частиц будут представлены двухрядными векторами-столбцами, где

${\begin{pmatrix}1\\0\end{pmatrix}}$

представляет собой нейтрон, и

${\begin{pmatrix}0\\1\end{pmatrix}}$

представляет собой протон (в представлении, где $\rho$ это обычный $\sigma _{z}$ спиновая матрица ).

Операторы, превращающие тяжелую частицу из протона в нейтрон и наоборот, соответственно представляются формулами

$Q=\sigma _{x}-i\sigma _{y}={\begin{pmatrix}0&1\\0&0\end{pmatrix}}$

и

$Q^{*}=\sigma _{x}+i\sigma _{y}={\begin{pmatrix}0&0\\1&0\end{pmatrix}}.$

$u_{n}$ соотв. $v_{n}$ является собственной функцией нейтрона соответственно. протон в состоянии $n$.

гамильтониан

Гамильтониан состоит из трех частей: $H_{\text{h.p.}}$, представляющий энергию свободных тяжелых частиц, $H_{\text{l.p.}}$, представляющая энергию свободных частиц света, и часть, дающая взаимодействие $H_{\text{int.}}$.

$H_{\text{h.p.}}={\frac {1}{2}}(1+\rho )N+{\frac {1}{2}}(1-\rho )P,$

где $N$ и $P$ являются операторами энергии нейтрона и протона соответственно, так что если $\rho =1$, $H_{\text{h.p.}}=N$, и если $\rho =-1$, $H_{\text{h.p.}}=P$.

$H_{\text{l.p.}}=\sum _{s}H_{s}N_{s}+\sum _{\sigma }K_{\sigma }M_{\sigma },$

где $H_{s}$ это энергия электрона в $s^{\text{th}}$ состояние в кулоновском поле ядра и $N_{s}$ – число электронов в этом состоянии; $M_{\sigma }$ количество нейтрино в $\sigma ^{\text{th}}$ государство, и $K_{\sigma }$ энергия каждого такого нейтрино (предполагается, что оно находится в свободном плосковолновом состоянии).

Часть взаимодействия должна содержать член, обозначающий превращение протона в нейтрон вместе с испусканием электрона и нейтрино (теперь известного как антинейтрино), а также член, обозначающий обратный процесс; Кулоновская сила между электроном и протоном игнорируется как не имеющая отношения к $\beta$-процесс распада.

Ферми предлагает два возможных значения для $H_{\text{int.}}$: во-первых, нерелятивистская версия, игнорирующая вращение:

$H_{\text{int.}}=g\left[Q\psi (x)\phi (x)+Q^{*}\psi ^{*}(x)\phi ^{*}(x)\right],$

и впоследствии версия, предполагающая, что легкие частицы являются четырехкомпонентными спинорами Дирака , но что скорость тяжелых частиц мала по сравнению с $c$ и что членами взаимодействия, аналогичными электромагнитному векторному потенциалу, можно пренебречь:

$H_{\text{int.}}=g\left[Q{\tilde {\psi }}^{*}\delta \phi +Q^{*}{\tilde {\psi }}\delta \phi ^{*}\right],$

где $\psi$ и $\phi$ теперь являются четырехкомпонентными спинорами Дирака, ${\tilde {\psi }}$ представляет собой эрмитово сопряжение $\psi$, и $\delta$ это матрица

${\begin{pmatrix}0&-1&0&0\\1&0&0&0\\0&0&0&1\\0&0&-1&0\end{pmatrix}}.$

Матричные элементы

Состояние системы считается заданным кортежем $\rho ,n,N_{1},N_{2},\ldots ,M_{1},M_{2},\ldots ,$ где $\rho =\pm 1$ определяет, является ли тяжелая частица нейтроном или протоном, $n$ — квантовое состояние тяжелой частицы, $N_{s}$ количество электронов в состоянии $s$ и $M_{\sigma }$ количество нейтрино в состоянии $\sigma$.

Используя релятивистскую версию $H_{\text{int.}}$, Ферми дает матричный элемент между состоянием с нейтроном в состоянии $n$ и нет электронов соответственно. нейтрино присутствуют в состоянии $s$ соотв. $\sigma$, и состояние с протоном в состоянии $m$ а электрон и нейтрино находятся в состояниях $s$ и $\sigma$ как

$H_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}=\pm g\int v_{m}^{*}u_{n}{\tilde {\psi }}_{s}\delta \phi _{\sigma }^{*}d\tau ,$

где интеграл берется по всему конфигурационному пространству тяжелых частиц (кроме $\rho$). $\pm$ определяется тем, является ли общее количество легких частиц нечетным (-) или четным (+).

Вероятность перехода

Смотрите также: золотое правило Ферми

Рассчитать время жизни нейтрона в состоянии $n$ согласно обычной квантовой теории возмущений , указанные выше матричные элементы необходимо просуммировать по всем незанятым электронным и нейтринным состояниям. Это упрощается, если предположить, что собственные функции электрона и нейтрино $\psi _{s}$ и $\phi _{\sigma }$ постоянны внутри ядра (т. е. их комптоновская длина волны намного больше размера ядра). Это приводит к

$H_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}=\pm g{\tilde {\psi }}_{s}\delta \phi _{\sigma }^{*}\int v_{m}^{*}u_{n}d\tau ,$

где $\psi _{s}$ и $\phi _{\sigma }$ теперь оцениваются по положению ядра.

По золотому правилу Ферми , вероятность этого перехода равна

${\begin{aligned}\left|a_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}\right|^{2}&=\left|H_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}\times {\frac {\exp {{\frac {2\pi i}{h}}(-W+H_{s}+K_{\sigma })t}-1}{-W+H_{s}+K_{\sigma }}}\right|^{2}\\&=4\left|H_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}\right|^{2}\times {\frac {\sin ^{2}\left({\frac {\pi t}{h}}(-W+H_{s}+K_{\sigma })\right)}{(-W+H_{s}+K_{\sigma })^{2}}},\end{aligned}}$

где $W$ – разность энергий состояний протона и нейтрона.

Усреднение по всем направлениям спина/импульса нейтрино с положительной энергией (где $\Omega ^{-1}$ – плотность состояний нейтрино, обращенная в итоге к бесконечности), получаем

$\left\langle \left|H_{\rho =-1,m,N_{s}=1,M_{\sigma }=1}^{\rho =1,n,N_{s}=0,M_{\sigma }=0}\right|^{2}\right\rangle _{\text{avg}}={\frac {g^{2}}{4\Omega }}\left|\int v_{m}^{*}u_{n}d\tau \right|^{2}\left({\tilde {\psi }}_{s}\psi _{s}-{\frac {\mu c^{2}}{K_{\sigma }}}{\tilde {\psi }}_{s}\beta \psi _{s}\right),$

где $\mu$ – масса покоя нейтрино и $\beta$ – матрица Дирака.

Учитывая, что вероятность перехода имеет резкий максимум для значений $p_{\sigma }$ для чего $-W+H_{s}+K_{\sigma }=0$, это упрощается до

$t{\frac {8\pi ^{3}g^{2}}{h^{4}}}\times \left|\int v_{m}^{*}u_{n}d\tau \right|^{2}{\frac {p_{\sigma }^{2}}{v_{\sigma }}}\left({\tilde {\psi }}_{s}\psi _{s}-{\frac {\mu c^{2}}{K_{\sigma }}}{\tilde {\psi }}_{s}\beta \psi _{s}\right),$

где $p_{\sigma }$ и $K_{\sigma }$ это ценности, для которых $-W+H_{s}+K_{\sigma }=0$.

Ферми делает три замечания по поводу этой функции:

• Поскольку состояния нейтрино считаются свободными, $K_{\sigma }>\mu c^{2}$ и, таким образом, верхний предел непрерывного $\beta$-спектр это $H_{s}\leq W-\mu c^{2}$.
• Поскольку для электронов $H_{s}>mc^{2}$, для того, чтобы $\beta$-чтобы произошел распад, разность энергий протона и нейтрона должна быть $W\geq (m+\mu )c^{2}$
• Фактор

$Q_{mn}^{*}=\int v_{m}^{*}u_{n}d\tau$

при переходе вероятность обычно равна единице, но в особых обстоятельствах она исчезает; это приводит к (приблизительным) правилам отбора для $\beta$-разлагаться.

Запрещенные переходы

Основная статья: Запрещенный переход

Как отмечалось выше, когда внутренний продукт $Q_{mn}^{*}$ между состояниями тяжелых частиц $u_{n}$ и $v_{m}$ исчезает, соответствующий переход «запрещен» (или, скорее, гораздо менее вероятен, чем в случаях, когда он ближе к 1).

Если описание ядра с точки зрения отдельных квантовых состояний протонов и нейтронов является точным с хорошим приближением, $Q_{mn}^{*}$ исчезает, если состояние нейтрона $u_{n}$ и состояние протона $v_{m}$ иметь одинаковый угловой момент; в противном случае необходимо использовать полный угловой момент всего ядра до и после распада.

Влияние

Вскоре после появления статьи Ферми Вернер Гейзенберг в письме Вольфгангу Паули отметил: что испускание и поглощение нейтрино и электронов в ядре должно во втором порядке теории возмущений приводить к притяжению между протонами и нейтронами, аналогично тому, как испускание и поглощение фотонов приводит к возникновению электромагнитной силы. Он обнаружил, что сила будет иметь вид ${\frac {\text{Const.}}{r^{5}}}$, но современные экспериментальные данные привели к значению, которое было слишком маленьким в миллион раз.

В следующем году Хидеки Юкава подхватил эту идею. но в его теории нейтрино и электроны были заменены новой гипотетической частицей с массой покоя примерно в 200 раз тяжелее электрона .

Более поздние события

Четырехфермионная теория Ферми описывает слабое взаимодействие замечательно . К сожалению, расчетное сечение или вероятность взаимодействия растет пропорционально квадрату энергии $\sigma \approx G_{\rm {F}}^{2}E^{2}$. Поскольку это сечение неограниченно растет, теория неприменима при энергиях, намного превышающих примерно 100 ГэВ. Здесь G _F — константа Ферми, обозначающая силу взаимодействия. В конечном итоге это привело к замене четырехфермионного контактного взаимодействия более полной теорией ( УФ-завершение ) — обменом W- или Z-бозоном , как это объясняется в электрослабой теории .

Взаимодействие Ферми, показывающее 4-точечный фермионный векторный ток, связанный константой связи GF _Ферми . Теория Ферми была первой теоретической попыткой описать скорость ядерного распада β-распада.

Взаимодействие также могло бы объяснить распад мюона посредством взаимодействия мюона, электрона-антинейтрино, мюона-нейтрино и электрона с той же фундаментальной силой взаимодействия. Эта гипотеза была выдвинута Герштейном и Зельдовичем и известна как гипотеза сохранения векторного тока.

В исходной теории Ферми предполагал, что формой взаимодействия является контактная связь двух векторных токов. указали Впоследствии Ли и Янг , что ничто не препятствует появлению осевого тока, нарушающего четность, и это было подтверждено экспериментами, проведенными Цзянь-Шюн Ву .

Включение нарушения четности во взаимодействие Ферми было сделано Джорджем Гамовым и Эдвардом Теллером в так называемых переходах Гамова – Теллера , которые описывали взаимодействие Ферми в терминах «разрешенных» распадов, нарушающих четность, и «сверхразрешенных» распадов, сохраняющих четность, в терминах антипараллельные и параллельные спиновые состояния электрона и нейтрино соответственно. До появления электрослабой теории и модели Стандартной Джордж Сударшан и Роберт Маршак , а также независимо Ричард Фейнман и Мюррей Гелл-Манн смогли определить правильную структуру тензора ( вектор минус аксиальный вектор , V — A ) из четырёх -фермионное взаимодействие.

постоянная Ферми

Наиболее точное экспериментальное определение константы Ферми достигается путем измерения времени жизни обратно пропорционально квадрату GF _{мюона , которое} (если пренебречь массой мюона относительно массы W-бозона). Говоря современным языком, «приведенная константа Ферми», то есть константа в натуральных единицах , равна

$G_{\rm {F}}^{0}={\frac {G_{\rm {F}}}{(\hbar c)^{3}}}={\frac {\sqrt {2}}{8}}{\frac {g^{2}}{M_{\rm {W}}^{2}c^{4}}}=1.1663787(6)\times 10^{-5}\;{\textrm {GeV}}^{-2}\approx 4.5437957\times 10^{14}\;{\textrm {J}}^{-2}\ .$

Здесь g — константа связи слабого взаимодействия , а M _W — масса W-бозона , опосредующего рассматриваемый распад.

В Стандартной модели константа Ферми связана с вакуумным математическим ожиданием Хиггса.

$v=\left({\sqrt {2}}\,G_{\rm {F}}^{0}\right)^{-1/2}\simeq 246.22\;{\textrm {GeV}}$.

Точнее, примерно (уровень дерева для стандартной модели),

$G_{\rm {F}}^{0}\simeq {\frac {\pi \alpha }{{\sqrt {2}}~M_{\rm {W}}^{2}(1-M_{\rm {W}}^{2}/M_{\rm {Z}}^{2})}}.$

Это можно еще упростить с точки зрения угла Вайнберга, используя соотношение между W- и Z-бозонами с $M_{\text{Z}}={\frac {M_{\text{W}}}{\cos \theta _{\text{W}}}}$, так что

$G_{\rm {F}}^{0}\simeq {\frac {\pi \alpha }{{\sqrt {2}}~M_{\rm {Z}}^{2}\cos ^{2}\theta _{\rm {W}}\sin ^{2}\theta _{\rm {W}}}}.$