Кривая Бланманже

График кривой бланманже.

В математике представляет кривая бланманже собой самоаффинную фрактальную кривую, которую можно построить путем деления средней точки. Она также известна как кривая Такаги , в честь Тейджи Такаги , который описал ее в 1901 году, или как кривая Такаги-Ландсберга , обобщение кривой, названной в честь Такаги и Георга Ландсберга . Название «бланманже» происходит от сходства с пудингом «бланманже» . Это частный случай более общей кривой де Рама .

Определение

Функция бланманже определяется на единичном интервале формулой

$\operatorname {blanc} (x)=\sum _{n=0}^{\infty }{s(2^{n}x) \over 2^{n}},$

где $s(x)$ — треугольная волна , определяемая формулой $s(x)=\min _{n\in {\mathbf {Z} }}|x-n|$, то есть, $s(x)$ — расстояние от x до ближайшего целого числа .

Кривая Такаги – Ландсберга представляет собой небольшое обобщение, определяемое формулой

$T_{w}(x)=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)$

для параметра $w$; таким образом, кривая бланманже имеет место $w=1/2$. Значение $H=-\log _{2}w$ известен как параметр Херста .

Функцию можно распространить на всю действительную линию: применение приведенного выше определения показывает, что функция повторяется на каждом единичном интервале.

Определение функционального уравнения

Периодическую версию кривой Такаги также можно определить как единственное ограниченное решение. $T=T_{w}:\mathbb {R} \to \mathbb {R}$ к функциональному уравнению

$T(x)=s(x)+wT(2x).$

Действительно, функция бланманже $T_{w}$ заведомо ограничен и решает функциональное уравнение, поскольку

$T_{w}(x):=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)=s(x)+\sum _{n=1}^{\infty }w^{n}s(2^{n}x)$$=s(x)+w\sum _{n=0}^{\infty }w^{n}s(2^{n+1}x)=s(x)+wT_{w}(2x).$

И наоборот, если $T:\mathbb {R} \to \mathbb {R}$ является ограниченным решением функционального уравнения, повторяющим равенство, которое имеет место для любого N

$T(x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+w^{N+1}T(2^{N+1}x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+o(1),{\text{ for }}N\to \infty ,$

откуда $T=T_{w}$. Кстати, приведенные выше функциональные уравнения имеют бесконечно много непрерывных неограниченных решений, например $T_{w}(x)+c|x|^{-\log _{2}w}.$

Графическое построение

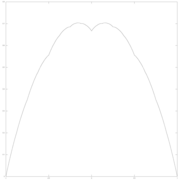
Кривую бланманже можно визуально построить из треугольных волновых функций, если бесконечную сумму аппроксимировать конечными суммами первых нескольких членов. На иллюстрациях ниже к кривой на каждом этапе добавляются все более тонкие функции треугольника (показаны красным).

п = 0	п ≤ 1	п ≤ 2	п ≤ 3

Характеристики

Конвергенция и преемственность

Бесконечная сумма, определяющая $T_{w}(x)$ сходится абсолютно для всех $x.$ С $0\leq s(x)\leq 1/2$ для всех $x\in \mathbb {R} ,$

$\sum _{n=0}^{\infty }|w^{n}s(2^{n}x)|\leq {\frac {1}{2}}\sum _{n=0}^{\infty }|w|^{n}={\frac {1}{2}}\cdot {\frac {1}{1-|w|}}$

если $|w|<1.$ Кривая параметра Такаги $w$ определяется на единичном интервале (или $\mathbb {R}$) если $|w|<1$. Функция Такаги параметра $w$ является непрерывным . Функции $T_{w,n}$ определяется частичными суммами

$T_{w,n}(x)=\sum _{k=0}^{n}w^{k}s(2^{k}x)$

непрерывны и сходятся равномерно к $T_{w}:$

${\begin{aligned}\left|T_{w}(x)-T_{w,n}(x)\right|&=\left|\sum _{k=n+1}^{\infty }w^{k}s(2^{k}x)\right|\\&=\left|w^{n+1}\sum _{k=0}^{\infty }w^{k}s(2^{k+n+1}x)\right|\\&\leq {\frac {|w|^{n+1}}{2}}\cdot {\frac {1}{1-|w|}}\end{aligned}}$

для всех х, когда $|w|<1.$ Эта граница уменьшается по мере $n\to \infty .$ По теореме равномерной предельной $T_{w}$ непрерывно, если | ш | < 1.

• 
  параметр w = 2/3
• 
  параметр w = 1/2
• 
  параметр w = 1/3
• 
  параметр w = 1/4
• 
  параметр w = 1/8

Субаддитивность

Поскольку абсолютное значение является субаддитивной функцией, то же самое относится и к функции $s(x)=\min _{n\in {\mathbf {Z} }}|x-n|$и его расширения $s(2^{k}x)$; поскольку положительные линейные комбинации и поточечные пределы субаддитивных функций субаддитивны, функция Такаги субаддитивна при любом значении параметра $w$.

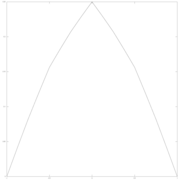
Частный случай параболы

Для $w=1/4$, получается парабола : построение параболы делением средней точки было описано Архимедом .

Дифференцируемость

Для значений параметра $0<w<1/2,$ функция Такаги $T_{w}$ дифференцируема в классическом смысле при любом $x\in \mathbb {R}$ что не является диадическим рациональным . Путем вывода под знаком ряда для любого недвоичного рационального $x\in \mathbb {R} ,$ можно найти

$T_{w}^{\prime }(x)=\sum _{n=0}^{\infty }(2w)^{n}\,(2b_{n}-1)$

где $(b_{n})_{n\in \mathbb {N} }\in \{0,1\}^{\mathbb {N} }$ это последовательность двоичных цифр в по основанию 2 разложении $x$:

$x=\sum _{n=-k}^{\infty }b_{n}2^{-n-1}\;.$

Эквивалентно, биты в двоичном представлении можно понимать как последовательность прямоугольных волн , вейвлетов Хаара , масштабированных по ширине. $2^{-n}.$ Это следует из того, что производная треугольной волны — это просто прямоугольная волна:

${\frac {d}{dx}}s(x)=\operatorname {sgn}(1/2-(x\!\!\!\mod 1))$

и так

$T_{w}^{\prime }(x)=\sum _{n=0}^{\infty }(2w)^{n}\operatorname {sgn}(1/2-(2^{n}x\!\!\!\mod 1))$

Для параметра $0<w<1/2,$ функция $T_{w}$ Липшица ​ константа $1/(1-2w).$ В частности, за особую ценность $w=1/4$ для любого недиадического рационального $x\in [0,1]$ $T_{1/4}'(x)=2-4x$, согласно упомянутому $T_{1/4}(x)=2x(1-x).$

Для $w=1/2$ функция бланманже $T_{w}$ он имеет ограниченную вариацию ни на одном непустом открытом множестве; оно даже не локально липшицево, а квазилипшицево, причем допускает функцию $\omega (t):=t(|\log _{2}t|+1/2)$ как модуль непрерывности .

Разложение в ряд Фурье

Функция Такаги–Ландсберга допускает абсолютно сходящийся разложение в ряд Фурье:

$T_{w}(x)=\sum _{m=0}^{\infty }a_{m}\cos(2\pi mx)$

с $a_{0}=1/4(1-w)$ и, для $m\geq 1$

$a_{m}:=-{\frac {2}{\pi ^{2}m^{2}}}(4w)^{\nu (m)},$

где $2^{\nu (m)}$ это максимальная мощность $2$ который разделяет $m$. Действительно, вышеупомянутая треугольная волна $s(x)$ имеет абсолютно сходящееся разложение в ряд Фурье

$s(x)={\frac {1}{4}}-{\frac {2}{\pi ^{2}}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{2}}}\cos {\big (}2\pi (2k+1)x{\big )}.$

Путем абсолютной сходимости можно переупорядочить соответствующий двойной ряд для $T_{w}(x)$:

$T_{w}(x):=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)={\frac {1}{4}}\sum _{n=0}^{\infty }w^{n}-{\frac {2}{\pi ^{2}}}\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{\frac {w^{n}}{(2k+1)^{2}}}\cos {\big (}2\pi 2^{n}(2k+1)x{\big )}\,:$

положить $m=2^{n}(2k+1)$ дает приведенный выше ряд Фурье для $T_{w}(x).$

Самоподобие

Рекурсивное определение позволяет задать моноид автосимметрий кривой. Этот моноид задается двумя генераторами, g и r , которые действуют на кривую (ограниченную единичным интервалом) как

$[g\cdot T_{w}](x)=T_{w}\left(g\cdot x\right)=T_{w}\left({\frac {x}{2}}\right)={\frac {x}{2}}+wT_{w}(x)$

и

$[r\cdot T_{w}](x)=T_{w}(r\cdot x)=T_{w}(1-x)=T_{w}(x).$

Тогда общий элемент моноида имеет вид $\gamma =g^{a_{1}}rg^{a_{2}}r\cdots rg^{a_{n}}$ для некоторых целых чисел $a_{1},a_{2},\cdots ,a_{n}$ Это действует на кривую как линейная функция : $\gamma \cdot T_{w}=a+bx+cT_{w}$ для некоторых констант a , b и c . Поскольку действие линейно, его можно описать в терминах векторного пространства с базисом векторного пространства :

$1\mapsto e_{1}={\begin{bmatrix}1\\0\\0\end{bmatrix}}$

$x\mapsto e_{2}={\begin{bmatrix}0\\1\\0\end{bmatrix}}$

$T_{w}\mapsto e_{3}={\begin{bmatrix}0\\0\\1\end{bmatrix}}$

В этом представлении действие g и r задается формулами

$g={\begin{bmatrix}1&0&0\\0&{\frac {1}{2}}&{\frac {1}{2}}\\0&0&w\end{bmatrix}}$

и

$r={\begin{bmatrix}1&1&0\\0&-1&0\\0&0&1\end{bmatrix}}$

То есть действие общего элемента $\gamma$ отображает кривую бланманже на единичном интервале [0,1] в подинтервал $[m/2^{p},n/2^{p}]$ для некоторых целых чисел m , n , p . Отображение задается именно выражением $[\gamma \cdot T_{w}](x)=a+bx+cT_{w}(x)$ где значения a , b и c могут быть получены непосредственно путем умножения вышеуказанных матриц. То есть:

$\gamma ={\begin{bmatrix}1&{\frac {m}{2^{p}}}&a\\0&{\frac {n-m}{2^{p}}}&b\\0&0&c\end{bmatrix}}$

Обратите внимание, что $p=a_{1}+a_{2}+\cdots +a_{n}$ является немедленным.

Моноид, порожденный g и r, иногда называют диадическим моноидом ; это субмоноид модульной группы . При обсуждении модульной группы более распространенными обозначениями g и r являются T и S , но эти обозначения конфликтуют с используемыми здесь символами.

Вышеупомянутое трехмерное представление — лишь одно из многих возможных представлений; оно показывает, что кривая бланманже является одной из возможных реализаций действия. То есть существуют представления для любого измерения, а не только для 3; некоторые из них дают кривые де Рама .

Интегрирование кривой Бланманже

Учитывая, интеграл что $\operatorname {blanc} (x)$ от 0 до 1 равно 1/2, тождество $\operatorname {blanc} (x)=\operatorname {blanc} (2x)/2+s(x)$ позволяет вычислять интеграл по любому интервалу с помощью следующего соотношения. Вычисления являются рекурсивными, время вычислений порядка логарифма требуемой точности. Определение

$I(x)=\int _{0}^{x}\operatorname {blanc} (y)\,dy$

у одного есть это

$I(x)={\begin{cases}I(2x)/4+x^{2}/2&{\text{if }}0\leq x\leq 1/2\\1/2-I(1-x)&{\text{if }}1/2\leq x\leq 1\\n/2+I(x-n)&{\text{if }}n\leq x\leq (n+1)\\\end{cases}}$

Определенный интеграл определяется выражением:

$\int _{a}^{b}\operatorname {blanc} (y)\,dy=I(b)-I(a).$

Более общее выражение можно получить, определив

$S(x)=\int _{0}^{x}s(y)dy={\begin{cases}x^{2}/2,&0\leq x\leq {\frac {1}{2}}\\-x^{2}/2+x-1/4,&{\frac {1}{2}}\leq x\leq 1\\n/4+S(x-n),&(n\leq x\leq n+1)\end{cases}}$

что в сочетании с представлением в виде ряда дает

$I_{w}(x)=\int _{0}^{x}T_{w}(y)dy=\sum _{n=0}^{\infty }(w/2)^{n}S(2^{n}x)$

Обратите внимание, что

$I_{w}(1)={\frac {1}{4(1-w)}}$

Этот интеграл также самоподобен на единичном интервале под действием диадического моноида, описанного в разделе Самоподобие . Здесь представление четырехмерное, имеющее базис $\{e_{1},e_{2},e_{3},e_{4}\}=\{1,x,x^{2},I_{w}(x)\}$. Действие g на единичном интервале представляет собой коммутационную диаграмму

$[g\cdot I_{w}](x)=I_{w}\left(g\cdot x\right)=I_{w}\left({\frac {x}{2}}\right)={\frac {x^{2}}{8}}+{\frac {w}{2}}I_{w}(x).$

Отсюда можно сразу считать генераторы четырехмерного представления:

$g={\begin{bmatrix}1&0&0&0\\0&{\frac {1}{2}}&0&0\\0&0&{\frac {1}{4}}&{\frac {1}{8}}\\0&0&0&{\frac {w}{2}}\end{bmatrix}}$

и

$r={\begin{bmatrix}1&1&1&{\frac {1}{4(1-w)}}\\0&-1&-2&0\\0&0&1&0\\0&0&0&-1\end{bmatrix}}$

Повторные интегралы преобразуются в 5,6,... мерном представлении.

Связь с симплициальными комплексами

Позволять

$N={\binom {n_{t}}{t}}+{\binom {n_{t-1}}{t-1}}+\ldots +{\binom {n_{j}}{j}},\quad n_{t}>n_{t-1}>\ldots >n_{j}\geq j\geq 1.$

Определите функцию Краскала–Катона.

$\kappa _{t}(N)={n_{t} \choose t+1}+{n_{t-1} \choose t}+\dots +{n_{j} \choose j+1}.$

Теорема Краскала –Катона утверждает, что это минимальное количество ( t − 1)-симплексов, которые являются гранями набора из N t -симплексов.

Поскольку t и N приближаются к бесконечности, $\kappa _{t}(N)-N$ (должным образом нормализованная) приближается к кривой бланманже.

См. также

• Функция Кантора (также известная как лестница дьявола)
• Функция вопросительного знака Минковского
• Функция Вейерштрасса
• Диадическая трансформация

Ссылки

• Вайсштейн, Эрик В. «Функция Бланманже» . Математический мир .
• Такаги, Тейдзи (1901), «Простой пример непрерывной функции без производной», Proc. Физ.-матем. Соц. Япония. , 1 : 176–177, дои : 10.11429/subutsuhokoku1901.1.F176
• Бенуа Мандельброт , «Фрактальные пейзажи без складок и с реками», опубликованная в «Науке фрактальных изображений » под ред. Хайнц-Отто Пейтген, Дитмар Саупе; Спрингер-Верлаг (1988), стр. 243–260.
• Линас Вепстас, Симметрии карт удвоения периода , (2004)
• Дональд Кнут , Искусство компьютерного программирования , том 4а. Комбинаторные алгоритмы, часть 1. ISBN   0-201-03804-8 . См. стр. 372–375.

Дальнейшее чтение

• Аллаарт, Питер К.; Кавамура, Кико (11 октября 2011 г.), Функция Такаги: опрос , arXiv : 1110.1691 , Bibcode : 2011arXiv1110.1691A
• Лагариас, Джеффри К. (17 декабря 2011 г.), Функция Такаги и ее свойства , arXiv : 1112.4205 , Bibcode : 2011arXiv1112.4205L

Внешние ссылки

• Такаги Эксплорер
• (Некоторые свойства функции Такаги)