Сложный анализ
Эта статья включает в себя список общих ссылок , но в ней не хватает достаточно соответствующих встроенных цитат . ( Март 2021 г. ) |
| Математический анализ → сложный анализ |
| Сложный анализ |
|---|
 |
| Комплексные числа |
| Сложные функции |
| Основная теория |
| Теория геометрической функции |
| Люди |
Сложный анализ , традиционно известный как теория функций сложной переменной , является ветвью математического анализа , которая исследует функции сложных чисел . Это полезно во многих ветвях математики, включая алгебраическую геометрию , теорию чисел , аналитическую комбинаторию и прикладную математику , а также в физике , включая ветви гидродинамики , термодинамики , квантовой механики и теории верителей . По расширению, использование сложного анализа также имеет применение в инженерных областях, таких как ядерная , аэрокосмическая , машиностровая и электротехника . [ 1 ]
В качестве дифференцируемой функции сложной переменной равна ее серии Тейлора (то есть аналитическая ), сложный анализ особенно связан с аналитическими функциями сложной переменной, то есть голоморфными функциями . Концепция может быть расширена на функции нескольких сложных переменных .
История
[ редактировать ]
Сложный анализ является одной из классических ветвей в математике, с корнями в 18 -м веке и только прежде. Важные математики, связанные со сложными числами, включают Эйлера , Гаусса , Римана , Коши , Гёста Миттаг-Леффлер , Вейерштрас и многих других в 20-м веке. Сложный анализ, в частности теория конформных отображений , имеет много физических применений, а также используется в теории аналитических чисел . В наше время он стал очень популярным благодаря новому повышению от сложной динамики и изображениями фракталов, создаваемых итерационными голоморфными функциями . Другое важное применение сложного анализа заключается в теории струн , которая исследует конформальные инварианты в теории квантовых поля .
Сложные функции
[ редактировать ]
Сложная функция - это функция от сложных чисел до сложных чисел. Другими словами, это функция, которая имеет (не обязательно правильное) подмножество комплексных чисел в качестве домена и сложных чисел в качестве кодомана . Предполагается, что сложные функции имеют домен, который содержит непустое открытое подмножество сложной плоскости .
Для любой сложной функции значения из домена и их изображений в диапазоне может быть разделен на реальные и мнимые части:
где все реально.
Другими словами, сложная функция может быть разложен в
- и
т.е. в две реальные функции ( , ) двух реальных переменных ( , ).
Точно так же любая сложная функция F на произвольном наборе x (является изоморфным , и, следовательно, в этом смысле это) может рассматриваться как упорядоченная пара из двух реальных функций : (re f , im f ) или, альтернативно, как векторная функция от x в
Некоторые свойства сложных функций (такие как непрерывность ) являются не чем иным, как соответствующими свойствами векторных ценных функций двух реальных переменных. Другие концепции сложного анализа, такие как дифференциация , являются прямыми обобщениями аналогичных концепций для реальных функций, но могут иметь очень разные свойства. В частности, каждая дифференцируемая сложная функция является аналитической (см. Следующий раздел), и две дифференцирующие функции, которые равны в окрестностях точки, равны на пересечении их домена (если домены связаны ). Последнее свойство является основой принципа аналитического продолжения расширять каждую реальную аналитическую функцию , который позволяет уникально для получения сложной аналитической функции, домен которой является целой сложной плоскостью с конечным количеством удаленных кривых дуг . Многие основные и специальные сложные функции определяются таким образом, включая сложную экспоненциальную функцию , сложные функции логарифма и тригонометрические функции .
Голоморфные функции
[ редактировать ]Сложные функции, которые дифференцируются в каждой точке открытого подмножества сложной плоскости, как говорят Полем В контексте сложного анализа производная в определяется как [ 2 ]
Внешне, это определение формально аналогично определению производной реальной функции. Однако сложные производные и дифференцируемые функции ведут себя значительно по -разному по сравнению с их реальными аналогами. В частности, для этого предела значение коэффициента разницы должно приближаться к одному и тому же комплексному числу, независимо от способа, к которым мы подходим в сложной плоскости. Следовательно, сложная дифференциация имеет гораздо более сильные последствия, чем реальная дифференциация. Например, голоморфные функции бесконечно дифференцируют , тогда как существование производного не требует существования ( n + 1) TH -производной для реальных функций. Кроме того, все голоморфные функции удовлетворяют более сильному условию аналитического анализа , что означает, что функция, в каждой точке в его домене, локально задается серией сходящейся мощности. По сути, это означает, что функционирует голоморф может быть аппроксимирован произвольно хорошо полиномами в некотором районе каждой точки в Полем Это резко контрастирует с дифференцируемыми реальными функциями; Существуют бесконечно дифференцируемые реальные функции, которые нигде аналитические; См. Незаналитическую плавную функцию § плавная функция, которая нигде не является реальной аналитической .
Большинство элементарных функций, включая экспоненциальную функцию , тригонометрические функции и все полиномиальные функции , адекватно расширены на сложные аргументы как функции , голоморфны по всей сложной плоскости, делая их целыми функциями , в то время как рациональные функции , где P и Q являются полиномами, являются голоморфными на доменах, которые исключают точки, где Q равно нулю. Такие функции, которые являются голоморфными повсюду, кроме набора изолированных точек, известны как мероморфные функции . С другой стороны, функции , , и не являются голоморфными нигде на сложной плоскости, как можно показать по их неспособности удовлетворить условия Коши -Римана (см. Ниже).
Важным свойством голоморфных функций является взаимосвязь между частичными производными их реальных и воображаемых компонентов, известных как условия Cauchy -Riemann . Если , определяется , где , голоморфно в регионе , тогда ,
С точки зрения реальных и воображаемых частей функции, U и V , это эквивалентно паре уравнений и , где подписки указывают частичную дифференциацию. Тем не менее, условия Cauchy -Riemann не характеризуют голоморфные функции, без дополнительных условий непрерывности (см. Теорему о том, что Tooman -Menchoff ).
Голоморфные функции демонстрируют некоторые замечательные особенности. Например, теорема Пикарда утверждает, что диапазон всей функции может занять только три возможных формы: , , или для некоторых Полем Другими словами, если два различных комплексных числа и не в диапазоне всей функции , затем это постоянная функция. Кроме того, голоморфная функция на подключенном открытом наборе определяется его ограничением любого непустового открытого подмножества.
Конформная карта
[ редактировать ]
В математике конформная карта - это функция , которая локально сохраняет углы , но не обязательно длины.
Более формально, пусть и быть открытыми подмножествами Полем Функция называется конформным (или сохраняющим угла) в точке Если он сохраняет углы между направленными кривыми через , а также сохранение ориентации. Конформные карты сохраняют как угла, так и формы бесконечно малых фигур, но не обязательно их размер или кривизны .
Конформное свойство может быть описано в терминах якобийской производной матрицы координатной трансформации . Трансформация конформна всякий раз, когда якобиан в каждой точке является положительным скалярным временем матрицей вращения ( ортогональной с определяющим). Некоторые авторы определяют конформность, чтобы включить отображения ориентации, чьи якобианцы могут быть написаны как любые скалярные времена в любую ортогональную матрицу. [ 3 ]
Для отображений в двух измерениях конформные сопоставления (сохраняющие ориентацию) являются именно точкой локально-изменчивых сложных аналитических функций. В трех и более высоких измерениях теорема Лиувиля резко ограничивает конформные отображения несколькими типами.
Понятие конформности естественным образом обобщается для карт между римановым или полудимерным коллекторами .Основные результаты
[ редактировать ]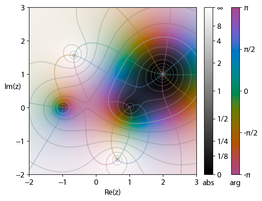
HUE представляет аргумент , яркость величины .
Одним из центральных инструментов в сложном анализе является линейный интеграл . Линия интеграл вокруг закрытого пути функции, которая является голоморфной повсюду внутри области, ограниченной закрытым пути, всегда нулевой, как указывает теорема Интеграла Коши . Значения такой голоморфной функции внутри диска могут быть рассчитаны с помощью интеграла пути на границе диска (как показано в интегральной формуле Коши ). теория остатков Интегралы пути в сложной плоскости часто используются для определения сложных реальных интегралов, и здесь применима (см. Методы интеграции контура ). «Полюс» (или изолированная сингулярность ) функции - это точка, когда значение функции становится неограниченным или «взрывается». Если функция имеет такой полюс, то можно вычислить остаток функции, который можно использовать для вычисления интегралов пути, включающих функцию; Это содержание теоремы мощного остатка . Замечательное поведение голоморфных функций вблизи важных особенностей описывается Теорема Пикарда . Функции, которые имеют только полюсы, но никаких существенных сингулярности называются мероморфными . Серия Laurent -это сложный эквивалент серии Тейлора , но они могут использоваться для изучения поведения функций вблизи сингулярности посредством бесконечных сумм более хорошо изученных функций, таких как полиномы.
Ограниченная функция , которая является голоморфной во всей сложной плоскости, должна быть постоянной; Это теорема Лиувиля . Он может быть использован для обеспечения естественного и короткого доказательства для фундаментальной теоремы алгебры , которая утверждает, что область комплексных чисел является алгебраически закрытым .
Если функция является голоморфной во всем соединенном домене, то ее значения полностью определяются ее значениями на любом меньшем субдомене. Говорят, что функция на более крупном домене аналитически продолжена от его значений в меньшей области. Это позволяет расширить определение функций, таких как функция Riemann Zeta , которые первоначально определяются в терминах бесконечных сумм, которые сходится только на ограниченных доменах почти во всей сложной плоскости. Иногда, как и в случае естественного логарифма , невозможно аналитически продолжить голоморфную функцию до не связанного домен Поверхность Римана .
Все это относится к сложному анализу в одной переменной. Существует также очень богатая теория сложного анализа более чем в одном сложном измерении в котором аналитические свойства, такие как мощности серии , расширение Полем Теорема картирования римана о конформной взаимосвязи определенных доменов в сложной плоскости, которая может быть наиболее важным результатом в одномерной теории, резко терпит неудачу в более высоких измерениях.
Основное применение определенных сложных пространств заключается в квантовой механике в качестве волновых функций .
Смотрите также
[ редактировать ]- Сложная геометрия
- Анализ гиперкомплекса
- Векторное исчисление
- Список комплексных темам анализов
- Теорема монодромии
- Реальный анализ
- Riemann - теорема Roch
- Теорема Рунге
Ссылки
[ редактировать ]- ^ «Промышленное применение сложного анализа» . Newton Gateway в математику . 30 октября 2019 года . Получено 20 ноября 2023 года .
- ^ Рудин, Уолтер (1987). Реальный и сложный анализ (PDF) . McGraw-Hill Education. п. 197. ISBN 978-0-07-054234-1 .
- ^ Блэр, Дэвид (2000-08-17). Теория инверсии и конформное картирование . Студенческая математическая библиотека. Тол. 9. Провиденс, Род -Айленд: Американское математическое общество. doi : 10.1090/stml/009 . ISBN 978-0-8218-2636-2 Полем S2CID 118752074 .
Источники
[ редактировать ]- Ablowitz, MJ & As Fokas , сложные переменные: введение и применение (Cambridge, 2003).
- Ahlfors, L. , сложный анализ (McGraw-Hill, 1953).
- Картан Х. , Элементарная теория аналитических функций одной или нескольких сложных переменных. (Hermann, 1961). Английский перевод, элементарная теория аналитических функций одной или нескольких сложных переменных. (Аддисон-Уэсли, 1963).
- Carathéodory, C. , Funktionentheorie. (Birkhäuser, 1950). Английский перевод, теория функций сложной переменной (Челси, 1954). [2 тома.]
- Carrier, GF , M. Krooke & Ce Pearson, Функции сложной переменной: теория и техника. (McGraw-Hill, 1966).
- Conway, JB , функции одной сложной переменной. (Springer, 1973).
- Фишер С., сложные переменные. (Wadsworth & Brooks/Cole, 1990).
- Форсайт А. Теория функций сложной переменной (Кембридж, 1893).
- Пятница, Э. и Р. Бусам, Функциональная теория . (Springer, 1995). Английский перевод, сложный анализ . (Springer, 2005).
- Goursat, E. , курс математического анализа, том 2 . (Gauthier-Villars, 1905). Английский перевод, раса математического анализа, вып. 2, часть 1: функции сложной переменной . (Джинн, 1916).
- Henrici, P. , прикладной и вычислительный комплексный анализ (Wiley). [Три тома: 1974, 1977, 1986.]
- Крейсзиг Э. , передовая инженерная математика. (Wiley, 1962).
- Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. ( Methods of the Theory of Functions of a Complex Variable ). (1951, in Russian).
- Markushevich, AI , Теория функций сложной переменной , (Prentice-Hall, 1965). [Три тома.]
- Marsden & Hoffman, Основной сложный анализ. (Freeman, 1973).
- Needham, T. , анализ визуального комплекса. (Оксфорд, 1997). http://usf.usfca.edu/vca/
- Реммерт Р. , Теория сложных функций . (Springer, 1990).
- Рудин В. , Реальный и сложный анализ. (McGraw-Hill, 1966).
- Shaw, WT, сложный анализ с Mathematica (Cambridge, 2006).
- Stein, E. & R. Shakarchi, сложный анализ. (Принстон, 2003).
- Sveshnikov, A. G. & A. N. Tikhonov , Теория функций комплексной переменной. (Nauka, 1967). English translation, The Theory Of Functions Of A Complex Variable (MIR, 1978).
- Titchmarsh, EC , теория функций. (Оксфорд, 1932).
- Wegert, E., визуальные комплексные функции . (Birkhäuser, 2012).
- Whittaker, ET & GN Watson , курс современного анализа . (Кембридж, 1902). 3 -е изд. (1920)





































