Магнитогидродинамика

Об академическом журнале см. Магнитогидродинамика (журнал) .

Плазму, составляющую Солнце, можно смоделировать как МГД-систему.

Моделирование МГД-вихревой задачи Орзага–Танга, известной модельной задачи для тестирования перехода к сверхзвуковой 2D МГД-турбулентности.

Магнитогидродинамика ( МГД ; также называемая магнитогидродинамикой или гидромагнетизмом) — это модель электропроводящих жидкостей , которая рассматривает все взаимопроникающие виды частиц вместе как единую непрерывную среду . В первую очередь он занимается низкочастотным крупномасштабным магнитным поведением в плазме и жидких металлах и находит применение во многих областях, включая космическую физику , геофизику , астрофизику и инженерию .

Слово магнитогидродинамика происходит от слов «магнито» — магнитное «гидро» поле, — вода и «динамика» — движение. Область МГД была инициирована Ханнесом Альфвеном , за что он получил Нобелевскую премию по физике в 1970 году.

История

МГД-описание электропроводящих жидкостей было впервые разработано Ханнесом Альфвеном в статье 1942 года, опубликованной в журнале Nature под названием «Существование электромагнитно-гидродинамических волн», в которой изложено его открытие того, что сейчас называется альфвеновскими волнами . Первоначально Альфвен называл эти волны «электромагнитно-гидродинамическими волнами»; однако в более поздней статье он отметил: «Поскольку термин «электромагнитно-гидродинамические волны» несколько сложен, возможно, было бы удобно назвать это явление «магнито-гидродинамическими» волнами».

Уравнения

В МГД движение в жидкости описывается с помощью линейных комбинаций средних движений отдельных частиц : плотности тока $\mathbf {J}$ и центра масс скорость $\mathbf {v}$. В данной жидкости каждый вид $\sigma$ имеет числовую плотность $n_{\sigma }$, масса $m_{\sigma }$, электрический заряд $q_{\sigma }$и средняя скорость $\mathbf {u} _{\sigma }$. Тогда общая массовая плотность жидкости равна ${\textstyle \rho =\sum _{\sigma }m_{\sigma }n_{\sigma }}$, а движение жидкости можно описать плотностью тока, выражаемой как

$\mathbf {J} =\sum _{\sigma }n_{\sigma }q_{\sigma }\mathbf {u} _{\sigma }$

а скорость центра масс выражается как:

$\mathbf {v} ={\frac {1}{\rho }}\sum _{\sigma }m_{\sigma }n_{\sigma }\mathbf {u} _{\sigma }.$

МГД можно описать набором уравнений, состоящим из уравнения неразрывности , уравнения движения , уравнения состояния , закона Ампера , закона Фарадея и закона Ома . Как и в случае любого описания жидкости в кинетической системе, приближение замыкания должно применяться к наивысшему моменту уравнения распределения частиц. Это часто достигается путем аппроксимации теплового потока посредством условия адиабатичности или изотермии .

В адиабатическом пределе, т. е. в предположении изотропного давления $p$ и изотропная температура, жидкость с показателем адиабаты $\gamma$, электрическое сопротивление $\eta$, магнитное поле $\mathbf {B}$и электрическое поле $\mathbf {E}$ можно описать непрерывным уравнением

${\frac {\partial \rho }{\partial t}}+\nabla \cdot \left(\rho \mathbf {v} \right)=0,$

уравнение состояния

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {p}{\rho ^{\gamma }}}\right)=0,$

уравнение движения

$\rho \left({\frac {\partial }{\partial t}}+\mathbf {v} \cdot \nabla \right)\mathbf {v} =\mathbf {J} \times \mathbf {B} -\nabla p,$

низкочастотный закон Ампера

$\mu _{0}\mathbf {J} =\nabla \times \mathbf {B} ,$

Закон Фарадея

${\frac {\partial \mathbf {B} }{\partial t}}=-\nabla \times \mathbf {E} ,$

и закон Ома

$\mathbf {E} +\mathbf {v} \times \mathbf {B} =\eta \mathbf {J} .$

Если взять ротор этого уравнения и использовать закон Ампера и закон Фарадея, получим уравнение индукции :

${\frac {\partial \mathbf {B} }{\partial t}}=\nabla \times (\mathbf {v} \times \mathbf {B} )+{\frac {\eta }{\mu _{0}}}\nabla ^{2}\mathbf {B} ,$

где $\eta /\mu _{0}$ - магнитная диффузия .

В уравнении движения силы Лоренца член $\mathbf {J} \times \mathbf {B}$ можно расширить, используя закон Ампера и тождество векторного исчисления, чтобы дать

$\mathbf {J} \times \mathbf {B} ={\frac {\left(\mathbf {B} \cdot \nabla \right)\mathbf {B} }{\mu _{0}}}-\nabla \left({\frac {B^{2}}{2\mu _{0}}}\right),$

где первый член в правой части — это сила магнитного натяжения , а второй член — сила магнитного давления .

Идеальный МГД

Ввиду бесконечной проводимости любое движение (перпендикулярное полю) жидкости относительно силовых линий запрещено, поскольку оно создаст бесконечные вихревые токи . Таким образом, вещество жидкости «привязывается» к силовым линиям...

Ханнес Альфвен , 1943 год.

Самая простая форма МГД, идеальная МГД , предполагает, что резистивный член $\eta \mathbf {J}$ в законе Ома мала по сравнению с другими членами, так что ее можно принять равной нулю. Это происходит в пределе больших магнитных чисел Рейнольдса , при которых магнитная индукция доминирует над магнитной диффузией масштабах скорости и длины . на рассматриваемых Следовательно, процессы в идеальной МГД, которые преобразуют магнитную энергию в кинетическую энергию, называемые идеальными процессами , не могут генерировать тепло и повышать энтропию .

Фундаментальной концепцией, лежащей в основе идеальной МГД, является теорема о вмороженном потоке , которая утверждает, что объемная жидкость и встроенное магнитное поле вынуждены двигаться вместе, так что можно сказать, что одно из них «связано» или «заморожено» с другим. Следовательно, любые две точки, которые движутся со скоростью объемной жидкости и лежат на одной и той же силовой линии магнитного поля, будут продолжать лежать на одной и той же силовой линии, даже если эти точки переносятся потоками жидкости в системе. Связь между жидкостью и магнитным полем фиксирует топологию магнитного поля в жидкости — например, если набор силовых линий магнитного поля завязан в узел, то они останутся таковыми до тех пор, пока жидкость имеет незначительное удельное сопротивление. Эта трудность в повторном соединении силовых линий магнитного поля позволяет сохранять энергию путем перемещения жидкости или источника магнитного поля. Затем энергия может стать доступной, если условия для идеальной МГД нарушатся, что позволит осуществить магнитное пересоединение , которое высвободит накопленную энергию из магнитного поля.

Идеальные МГД-уравнения

В идеальной МГД резистивный член $\eta \mathbf {J}$ исчезает в законе Ома, давая идеальный закон Ома,

$\mathbf {E} +\mathbf {v} \times \mathbf {B} =0.$

Аналогично, член магнитной диффузии $\eta \nabla ^{2}\mathbf {B} /\mu _{0}$ в уравнении индукции обращается в нуль, давая идеальное уравнение индукции:

${\frac {\partial \mathbf {B} }{\partial t}}=\nabla \times (\mathbf {v} \times \mathbf {B} ).$

Применимость идеальной МГД к плазме

Идеальная МГД строго применима только тогда, когда:

1. Плазма сильно столкновительна, поэтому временной масштаб столкновений короче, чем другие характерные времена в системе, и поэтому распределения частиц близки к максвелловским .
2. Удельное сопротивление вследствие этих столкновений невелико. В частности, типичное время магнитной диффузии на любом масштабе, присутствующем в системе, должно быть больше, чем любой интересующий временной масштаб.
3. Интерес представляют масштабы длины, намного превышающие глубину скин-слоя иона и ларморовский радиус , перпендикулярный полю, достаточно длинные вдоль поля, чтобы игнорировать затухание Ландау , и масштабы времени, намного превышающие время вращения иона (система является гладкой и медленно развивающейся).

Важность удельного сопротивления

В жидкости с неидеальной проводимостью магнитное поле обычно может перемещаться через жидкость по закону диффузии, при этом удельное сопротивление плазмы служит константой диффузии . Это означает, что решения идеальных уравнений МГД применимы только в течение ограниченного времени для области заданного размера, прежде чем диффузия станет слишком важной, чтобы ее можно было игнорировать. Можно оценить время диффузии через активную область Солнца (по столкновительному сопротивлению) в сотни или тысячи лет, что намного дольше, чем фактическое время жизни солнечного пятна, поэтому кажется разумным игнорировать удельное сопротивление. Напротив, в метровом объеме морской воды время магнитной диффузии измеряется миллисекундами.

Даже в физических системах — которые большие и достаточно проводящие, так что простые оценки числа Лундквиста позволяют предположить, что удельное сопротивление можно игнорировать — удельное сопротивление все еще может быть важным: существует множество нестабильностей , которые могут увеличить эффективное удельное сопротивление плазмы более чем в 10 раз. ⁹ . Повышенное удельное сопротивление обычно является результатом образования мелкомасштабной структуры, такой как токовые слои или мелкомасштабная магнитная турбулентность , привносящая в систему небольшие пространственные масштабы, в которых идеальная МГД нарушается и магнитная диффузия может происходить быстро. Когда это происходит, в плазме может произойти магнитное пересоединение с высвобождением накопленной магнитной энергии в виде волн, объемного механического ускорения материала, ускорения частиц и тепла.

Магнитное пересоединение в системах с высокой проводимостью важно, поскольку оно концентрирует энергию во времени и пространстве, поэтому мягкие силы, приложенные к плазме в течение длительных периодов времени, могут вызвать сильные взрывы и всплески радиации.

Когда жидкость нельзя считать полностью проводящей, но другие условия идеальной МГД соблюдены, можно использовать расширенную модель, называемую резистивной МГД. Это включает в себя дополнительный член закона Ома, который моделирует столкновительное сопротивление. Обычно компьютерное моделирование МГД является, по крайней мере, в некоторой степени резистивным, поскольку их расчетная сетка вводит числовое удельное сопротивление .

Структуры в МГД-системах

Дополнительная информация: Движение частиц магнитосферы.

Схематическое изображение различных токовых систем, формирующих магнитосферу Земли.

Во многих МГД-системах большая часть электрического тока сжимается в тонкие почти двумерные ленты, называемые токовыми слоями . Они могут разделить жидкость на магнитные домены, внутри которых токи относительно слабы. Текущие листы вСчитается, что толщина солнечной короны составляет от нескольких метров до нескольких километров, что довольно мало по сравнению с магнитными доменами (диаметр которых составляет от тысяч до сотен тысяч километров). Земли Другой пример – магнитосфера Земли , где токовые слои разделяют топологически различные области, изолируя большую часть ионосферы от солнечного ветра .

Волны

Смотрите также: Волны в плазме.

Волновые моды, полученные с помощью уравнений МГД, называются магнитогидродинамическими волнами или МГД-волнами . Существует три волновых режима МГД, которые можно вывести из линеаризованных уравнений идеальной МГД для жидкости с однородным и постоянным магнитным полем:

• Альфвеновские волны
• Медленные магнитозвуковые волны
• Быстрые магнитозвуковые волны

Фазовая скорость, построенная относительно θ

v _А > v _s

v _А < v _s

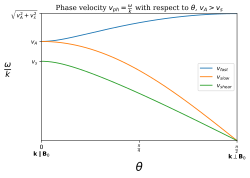
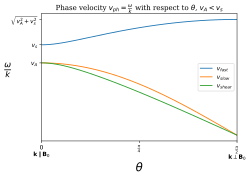
Фазовые скорости этих мод не зависят от величины волнового вектора, поэтому они не испытывают дисперсии. Фазовая скорость зависит от угла между волновым вектором k и магнитным B. полем МГД-волна, распространяющаяся под произвольным углом θ по отношению к независимому от времени или объемному полю B _0, будет удовлетворять дисперсионному соотношению

${\frac {\omega }{k}}=v_{A}\cos \theta$

где

$v_{A}={\frac {B_{0}}{\sqrt {\mu _{0}\rho }}}$

— альфвеновская скорость. Эта ветвь соответствует сдвиговой альфвеновской моде. Кроме того, дисперсионное уравнение дает

${\frac {\omega }{k}}=\left({\tfrac {1}{2}}\left(v_{A}^{2}+v_{s}^{2}\right)\pm {\tfrac {1}{2}}{\sqrt {\left(v_{A}^{2}+v_{s}^{2}\right)^{2}-4v_{s}^{2}v_{A}^{2}\cos ^{2}\theta }}\right)^{\frac {1}{2}}$

где

$v_{s}={\sqrt {\frac {\gamma p}{\rho }}}$

— идеальная скорость звука в газе. Плюсовая ветвь соответствует режиму быстрых МГД-волн, а минусовая ветвь соответствует режиму медленных МГД-волн. Приведен краткий обзор свойств этих волн:

Режим	Тип	Ограничение фазовых скоростей		Групповая скорость	Направление потока энергии
		$\mathbf {k} \parallel \mathbf {B}$	$\mathbf {k} \perp \mathbf {B}$
Альфвеновская волна	поперечный; несжимаемый	$v_{A}$	$0$	${\frac {\mathbf {B} }{\sqrt {\mu _{0}\rho }}}$	$\mathbf {Q} \parallel \mathbf {B}$
Быстрая магнитозвуковая волна	ни поперечный, ни продольный; компрессионный	$\max(v_{A},v_{s})$	${\sqrt {v_{A}^{2}+v_{s}^{2}}}$	равна фазовой скорости	ок. $\mathbf {Q} \parallel \mathbf {k}$
Медленная магнитозвуковая волна		$\min(v_{A},v_{s})$	$0$		ок. $\mathbf {Q} \parallel \mathbf {B}$

МГД-колебания будут затухать, если жидкость не является идеально проводящей, но имеет конечную проводимость или если присутствуют эффекты вязкости.

МГД-волны и колебания — популярный инструмент для дистанционной диагностики лабораторной и астрофизической плазмы, например, короны Солнца ( корональная сейсмология ).

Расширения

Резистивный

Резистивная МГД описывает намагниченные жидкости с конечной диффузией электронов ( η ≠ 0 ). Эта диффузия приводит к нарушению магнитной топологии; Линии магнитного поля могут «воссоединиться» при столкновении. Обычно этот срок невелик, и воссоединение можно рассматривать, думая о нем как о чем-то похожем на шок ; Было показано, что этот процесс важен для магнитных взаимодействий Земли и Солнца.

Расширенный

Расширенная МГД описывает класс явлений в плазме более высокого порядка, чем резистивная МГД, но которые можно адекватно рассматривать с помощью описания одной жидкости. К ним относятся эффекты физики Холла, градиенты электронного давления, конечные ларморовские радиусы в гиродвижении частиц и инерция электронов.

Двухжидкостный

Двухжидкостная МГД описывает плазму, которая включает в себя немалое электрическое поле Холла . В результате импульсы электронов и ионов необходимо рассматривать отдельно. Это описание более тесно связано с уравнениями Максвелла, поскольку существует уравнение эволюции электрического поля.

Зал

В 1960 году М. Дж. Лайтхилл раскритиковал применимость идеальной или резистивной МГД-теории для плазмы. Речь шла о пренебрежении « членом тока Холла » в законе Ома, частом упрощении, применяемом в теории магнитного синтеза. Магнитогидродинамика Холла (HMHD) учитывает это описание магнитогидродинамики электрическим полем, и закон Ома принимает форму

$\mathbf {E} +\mathbf {v} \times \mathbf {B} \underbrace {-{\frac {1}{n_{e}e}}(\mathbf {J} \times \mathbf {B} )} _{\text{Hall current term}}=\eta \mathbf {J} ,$

где $n_{e}$ - плотность электронов и $e$ это элементарный заряд . Самое важное отличие состоит в том, что при отсутствии разрыва силовой линии магнитное поле привязано к электронам, а не к объемной жидкости.

Электронная МГД

Электронная магнитогидродинамика (ЭМГД) описывает плазму небольших масштабов, когда движение электронов намного быстрее, чем ионов. Основными эффектами являются изменения законов сохранения, дополнительное сопротивление, важность инерции электронов. Многие эффекты Электронной МГД аналогичны эффектам Двухжидкостной МГД и МГД Холла. ЭМГД особенно важна для z-пинча , магнитного пересоединения , ионных двигателей , нейтронных звезд и плазменных переключателей.

Бесстолкновительный

МГД также часто используется для бесстолкновительной плазмы. В этом случае уравнения МГД выводятся из уравнения Власова .

Уменьшенный

Используя многомасштабный анализ, (резистивные) уравнения МГД можно свести к набору из четырех замкнутых скалярных уравнений. Это позволяет, среди прочего, проводить более эффективные численные расчеты.

Ограничения

Важность кинетических эффектов

Еще одним ограничением МГД (и теории жидкости в целом) является то, что они зависят от предположения, что плазма является сильно столкновительной (это первый критерий, перечисленный выше), поэтому временной масштаб столкновений короче, чем другие характерные времена в система, а распределения частиц максвелловские . Обычно этого не происходит в термоядерной, космической и астрофизической плазме. Когда это не так или интерес проявляется в меньших пространственных масштабах, может возникнуть необходимость использовать кинетическую модель, которая должным образом учитывает немаксвелловскую форму функции распределения. Однако, поскольку МГД относительно проста и отражает многие важные свойства динамики плазмы, она часто качественно точна и поэтому часто является первой опробованной моделью.

Эффекты, которые по существу являются кинетическими и не отражаются моделями жидкости, включают двойные слои , затухание Ландау , широкий диапазон нестабильностей, химическое разделение в космической плазме и убегание электронов. В случае лазерных взаимодействий сверхвысокой интенсивности невероятно короткие сроки выделения энергии означают, что гидродинамические коды не могут уловить суть физики.

Приложения

Геофизика

Под мантией Земли находится ядро, состоящее из двух частей: твердого внутреннего ядра и жидкого внешнего ядра. Оба содержат значительное количество железа . Жидкое внешнее ядро ​​движется в присутствии магнитного поля, и в нем возникают вихри из-за эффекта Кориолиса . Эти вихри создают магнитное поле, которое усиливает исходное магнитное поле Земли — процесс, который является самоподдерживающимся и называется геомагнитным динамо.

Инверсия магнитного поля Земли

На основе уравнений МГД Глатцмайер и Пол Робертс создали суперкомпьютерную модель недр Земли. После запуска моделирования в течение тысяч лет в виртуальном времени можно изучить изменения магнитного поля Земли. Результаты моделирования хорошо согласуются с наблюдениями, поскольку моделирование правильно предсказало, что магнитное поле Земли меняется каждые несколько сотен тысяч лет. Во время переворотов магнитное поле не исчезает совсем — оно просто становится более сложным.

Землетрясения

Некоторые станции мониторинга сообщают, что землетрясениям иногда предшествует всплеск сверхнизкочастотной (УНЧ) активности. Замечательный пример этого произошел перед землетрясением в Лома Приета в Калифорнии в 1989 году . хотя последующее исследование показало, что это было не более чем неисправность датчика. 9 декабря 2010 года учёные-геологи объявили, что спутник DEMETER наблюдал резкое усиление УНЧ-радиоволн над Гаити за месяц до землетрясения магнитудой 7,0 М _в 2010 году . Исследователи пытаются узнать больше об этой корреляции, чтобы выяснить, можно ли использовать этот метод как часть системы раннего предупреждения о землетрясениях.

Космическая физика

Исследование космической плазмы вблизи Земли и во всей Солнечной системе известно как космическая физика . Области исследований в области космической физики охватывают большое количество тем: от ионосферы до полярных сияний Земли , магнитосферы , солнечного ветра и корональных выбросов массы .

МГД формирует основу для понимания того, как популяции плазмы взаимодействуют в локальной геокосмической среде. Исследователи разработали глобальные модели, используя МГД для моделирования явлений в магнитосфере Земли, таких как расположение магнитопаузы Земли. (граница между магнитным полем Земли и солнечным ветром), образование кольцевого тока , авроральных электроджетов , и геомагнитно-индуцированные токи .

Одним из видных применений глобальных МГД-моделей является прогнозирование космической погоды . Интенсивные солнечные бури могут нанести серьезный ущерб спутникам и инфраструктуры, поэтому крайне важно, чтобы такие события обнаруживались на ранней стадии. Центр прогнозирования космической погоды (SWPC) использует модели MHD для прогнозирования прибытия и воздействия явлений космической погоды на Землю.

Астрофизика

МГД применяется к астрофизике , включая звезды, межпланетную среду (пространство между планетами) и, возможно, внутри межзвездной среды (пространство между звездами) и джеты . Большинство астрофизических систем не находятся в локальном тепловом равновесии и поэтому требуют дополнительной кинематической обработки для описания всех явлений внутри системы (см. Астрофизическая плазма ).

Солнечные пятна вызваны магнитными полями Солнца, как предположил Джозеф Лармор в 1919 году. Солнечным ветром также управляет МГД. Дифференциальное вращение Солнца может быть долговременным эффектом магнитного сопротивления на полюсах Солнца, явлением МГД, возникающим из-за формы спирали Паркера , которую принимает расширенное магнитное поле Солнца.

Раньше теории, описывающие формирование Солнца и планет, не могли объяснить, почему Солнце имеет 99,87% массы, но при этом лишь 0,54% углового момента Солнечной системы . В закрытой системе, такой как облако газа и пыли, из которого образовалось Солнце, масса и угловой момент сохраняются . Это сохранение означало бы, что по мере того, как масса концентрируется в центре облака, образуя Солнце, оно будет вращаться быстрее, подобно конькобежцу, втягивающему руки. Высокая скорость вращения, предсказанная ранними теориями, отбросила бы прото -Солнце друг от друга до того, как оно могло образоваться. Однако магнитогидродинамические эффекты передают угловой момент Солнца во внешнюю Солнечную систему, замедляя его вращение.

Известно, что распад идеальной МГД (в форме магнитного пересоединения) является вероятной причиной солнечных вспышек . Магнитное поле в солнечной активной области над пятном может накапливать энергию, которая высвобождается внезапно в виде всплеска движения, рентгеновских лучей и излучения , когда основной токовый слой сжимается, повторно соединяя поле.

Сплав с магнитным удержанием

МГД описывает широкий спектр физических явлений, происходящих в термоядерной плазме в таких устройствах, как токамаки или стеллараторы .

Уравнение Града-Шафранова, полученное на основе идеальной МГД, описывает равновесие осесимметричной тороидальной плазмы в токамаке. В экспериментах на токамаке равновесие во время каждого разряда регулярно рассчитывается и восстанавливается, что дает информацию о форме и положении плазмы, контролируемой токами во внешних катушках.

Известно, что теория стабильности МГД определяет эксплуатационные пределы токамаков. Например, идеальные режимы МГД-кинка обеспечивают жесткие ограничения на достижимую бета-версию плазмы ( предел Тройона ) и плазменный ток (устанавливаемый $q>2$ требование фактора безопасности ).

Датчики

Магнитогидродинамические датчики используются для прецизионных измерений угловых скоростей в инерциальных навигационных системах, например в аэрокосмической технике . Точность повышается с увеличением размера датчика. Датчик способен выживать в суровых условиях.

Инженерное дело

МГД связана с инженерными проблемами, такими как удержание плазмы , жидкометаллическое охлаждение ядерных реакторов и электромагнитное литье (среди прочих).

или Магнитогидродинамический привод МГД-движитель — это метод движения морских судов с использованием только электрических и магнитных полей без движущихся частей с использованием магнитогидродинамики. Принцип работы заключается в электрификации топлива (газа или воды), которое затем можно направить с помощью магнитного поля, толкая транспортное средство в противоположном направлении. Хотя существуют некоторые рабочие прототипы, MHD-приводы остаются непрактичными.

Первый прототип такого рода двигательной установки был построен и испытан в 1965 году Стюардом Уэйем, профессором машиностроения Калифорнийского университета в Санта-Барбаре . Уэй, находившийся в отпуске с работы в Westinghouse Electric , поручил своим студентам старших курсов разработать подводную лодку с этой новой двигательной установкой. В начале 1990-х годов фонд в Японии (Ship & Ocean Foundation (Минато-ку, Токио)) построил экспериментальную лодку « Ямато-1» , которая использовала магнитогидродинамический привод, включающий сверхпроводник , охлаждаемый жидким гелием , и могла двигаться со скоростью 15 км/ч.

Производство электроэнергии МГД , работающее на сжигании углекислого газа с затравкой калия, показало потенциал для более эффективного преобразования энергии (отсутствие твердых движущихся частей позволяет работать при более высоких температурах), но не удалось из-за непомерно высоких технических трудностей. Одной из серьезных инженерных проблем было разрушение стенки камеры сгорания первичного угля из-за истирания.

В микрофлюидике МГД изучается как жидкостный насос для создания непрерывного непульсирующего потока в сложной конструкции микроканалов.

МГД может быть реализована в процессе непрерывной разливки металлов для подавления нестабильностей и управления потоком.

Проблемы промышленной МГД можно моделировать с помощью программного обеспечения EOF-Library с открытым исходным кодом. Два примера моделирования: 3D МГД со свободной поверхностью для плавления с помощью электромагнитной левитации , и перемешивание жидкого металла вращающимися постоянными магнитами.

Магнитное нацеливание на наркотики

Важной задачей в исследованиях рака является разработка более точных методов доставки лекарств в пораженные районы. Один из методов предполагает связывание лекарства с биологически совместимыми магнитными частицами (такими как феррожидкости), которые направляются к цели посредством тщательного размещения постоянных магнитов на внешнем теле. Уравнения магнитогидродинамики и анализ методом конечных элементов используются для изучения взаимодействия между частицами магнитной жидкости в кровотоке и внешним магнитным полем.

См. также

• Вычислительная магнитогидродинамика
• Электрогидродинамика
• Электромагнитный насос
• Феррожидкость
• Измеритель скорости силы Лоренца
• Магнитный расходомер
• Магнитогидродинамический генератор
• Магнитогидродинамическая турбулентность
• Расплавленная соль
• Стабильность плазмы
• Удары и разрывы (магнитогидродинамика)
• Список учебников по электромагнетизму

Дальнейшее чтение

• Галтье, Себастьен (2016). Введение в современную магнитогидродинамику . Издательство Кембриджского университета . ISBN  9781107158658 .