Геодезический эффект

Эта статья о прецессии орбитальных тел. О наблюдении двойных звезд см. Эксперимент де Ситтера с двойной звездой .

Представление геодезического эффекта со значениями для Gravity Probe B .

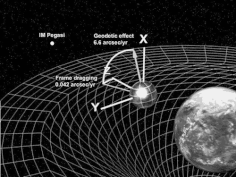
Геодезический эффект (также известный как геодезическая прецессия , прецессия де Ситтера или эффект де Ситтера ) представляет собой эффект кривизны пространства-времени , предсказанный общей теорией относительности , на вектор, увлекаемый вместе с вращающимся по орбите телом. Например, вектором может быть угловой момент гироскопа, вращающегося вокруг Земли, как это было выполнено в Gravity Probe B. эксперименте Геодезический эффект был впервые предсказан Виллемом де Ситтером в 1916 году, который внес релятивистские поправки в движение системы Земля-Луна. Работа Де Ситтера была расширена в 1918 году Яном Схоутеном и в 1920 году Адрианом Фоккером . Его также можно применить к определенной вековой прецессии астрономических орбит, эквивалентной вращению вектора Лапласа – Рунге – Ленца .

Термин «геодезический эффект» имеет два несколько разных значения, поскольку движущееся тело может вращаться или не вращаться. Невращающиеся тела движутся по геодезическим , тогда как вращающиеся тела движутся по немного другим орбитам.

Разница между прецессией де Ситтера и прецессией Лензе – Тирринга (перетаскиванием системы отсчета) заключается в том, что эффект де Ситтера обусловлен просто наличием центральной массы, тогда как прецессия Лензе – Тирринга обусловлена ​​вращением центральной массы. Полная прецессия рассчитывается путем объединения прецессии де Ситтера с прецессией Лензе – Тирринга.

Экспериментальное подтверждение

Геодезический эффект был подтвержден с точностью более 0,5% с помощью Gravity Probe B — эксперимента, измеряющего наклон оси вращения гироскопов на орбите вокруг Земли. Первые результаты были объявлены 14 апреля 2007 года на заседании Американского физического общества .

Формулы

Чтобы вывести прецессию, предположим, что система находится во вращающейся метрике Шварцшильда . Невращающаяся метрика

$ds^{2}=dt^{2}\left(1-{\frac {2m}{r}}\right)-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi '^{2}),$

где с = G = 1.

Введем вращающуюся систему координат с угловой скоростью $\omega$, такой, что спутник, находящийся на круговой орбите в плоскости θ = π/2, остается в покое. Это дает нам

$d\phi =d\phi '-\omega \,dt.$

В этой системе координат наблюдатель в радиальной позиции r видит вектор, расположенный в r, как вращающийся с угловой частотой ω. Однако этот наблюдатель видит вектор, расположенный при каком-то другом значении r , как вращающийся с другой скоростью из-за релятивистского замедления времени. Преобразуя метрику Шварцшильда во вращающуюся систему отсчета и предполагая, что $\theta$ является константой, мы находим

${\begin{aligned}ds^{2}&=\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)\left(dt-{\frac {r^{2}\beta \omega }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi \right)^{2}-\\&-dr^{2}\left(1-{\frac {2m}{r}}\right)^{-1}-{\frac {r^{2}\beta -2mr\beta }{1-2m/r-r^{2}\beta \omega ^{2}}}\,d\phi ^{2},\end{aligned}}$

с $\beta =\sin ^{2}(\theta )$. Для тела, вращающегося в плоскости θ = π/2, мы будем иметь β = 1, и мировая линия тела будет сохранять постоянные пространственные координаты все время. Теперь метрика имеет канонический вид

$ds^{2}=e^{2\Phi }\left(dt-w_{i}\,dx^{i}\right)^{2}-k_{ij}\,dx^{i}\,dx^{j}.$

Из этой канонической формы мы можем легко определить скорость вращения гироскопа в нужное время.

${\begin{aligned}\Omega &={\frac {\sqrt {2}}{4}}e^{\Phi }[k^{ik}k^{jl}(\omega _{i,j}-\omega _{j,i})(\omega _{k,l}-\omega _{l,k})]^{1/2}=\\&={\frac {{\sqrt {\beta }}\omega (r-3m)}{r-2m-\beta \omega ^{2}r^{3}}}={\sqrt {\beta }}\omega .\end{aligned}}$

где последнее равенство верно только для свободно падающих наблюдателей, для которыхускорения нет, поэтому $\Phi ,_{i}=0$. Это приводит к

$\Phi ,_{i}={\frac {2m/r^{2}-2r\beta \omega ^{2}}{2(1-2m/r-r^{2}\beta \omega ^{2})}}=0.$

Решение этого уравнения для ω дает

$\omega ^{2}={\frac {m}{r^{3}\beta }}.$

По сути, это закон периодов Кеплера , который оказывается релятивистски точным, если выражаться через временную координату t этой конкретной вращающейся системы координат. Во вращающейся системе отсчета спутник остается в покое, но наблюдатель на борту спутника видит, что вектор углового момента гироскопа прецессирует со скоростью ω. Этот наблюдатель также видит вращающиеся далекие звезды, но они вращаются с немного другой скоростью из-за замедления времени. гироскопа Пусть τ — собственное время . Затем

$\Delta \tau =\left(1-{\frac {2m}{r}}-r^{2}\beta \omega ^{2}\right)^{1/2}\,dt=\left(1-{\frac {3m}{r}}\right)^{1/2}\,dt.$

Член −2 m / r интерпретируется как гравитационное замедление времени, а дополнительный − m / r обусловлен вращением этой системы отсчета. Пусть α' — накопленная прецессия во вращающейся системе отсчета. С $\alpha '=\Omega \Delta \tau$, прецессия на протяжении одной орбиты относительно далеких звезд определяется выражением:

$\alpha =\alpha '+2\pi =-2\pi {\sqrt {\beta }}{\Bigg (}\left(1-{\frac {3m}{r}}\right)^{1/2}-1{\Bigg )}.$

первого порядка, Используя ряд Тейлора мы находим

$\alpha \approx {\frac {3\pi m}{r}}{\sqrt {\beta }}={\frac {3\pi m}{r}}\sin(\theta ).$

Прецессия Томаса

Можно попытаться разложить прецессию де Ситтера на кинематический эффект, называемый прецессией Томаса, в сочетании с геометрическим эффектом, вызванным гравитационно искривленным пространством-временем. Хоть один автор действительно описывает это именно так, но другие утверждают, что «прецессия Томаса вступает в силу для гироскопа на поверхности Земли…, но не для гироскопа на свободно движущемся спутнике». Возражением против первой интерпретации является то, что требуемая прецессия Томаса имеет неверный знак. Уравнение переноса Ферми -Уокера дает как геодезический эффект, так и прецессию Томаса и описывает перенос 4-вектора спина при ускоренном движении в искривленном пространстве-времени. 4-вектор спина ортогонален 4-вектору скорости. Транспорт Ферми-Уокера сохраняет это соотношение. Если ускорения нет, транспорт Ферми-Уокера представляет собой просто параллельный транспорт вдоль геодезической и дает прецессию спина из-за геодезического эффекта. Для ускорения, обусловленного равномерным круговым движением в плоском пространстве-времени Минковского, транспорт Ферми-Уокера дает прецессию Томаса.

См. также

• Перетаскивание кадров
• Геодезика в общей теории относительности
• Гравитационный колодец
• Хронология гравитационной физики и теории относительности

Ссылки

• Вольфганг Риндлер (2006) Относительность: специальная, общая и космологическая (2-е изд.), Oxford University Press, ISBN   978-0-19-856731-8

Внешние ссылки

• Веб-сайты Gravity Probe B в НАСА и Стэнфордском университете
• Прецессия в искривленном пространстве «Геодезический эффект»
• Геодезический эффект