Стехиометрия

Стехиометрическая диаграмма реакции метана горения .

Стехиометрия ( / ˌ s t ɔɪ k i ˈ ɒ m ɪ t r i / ) — это соотношение между массами реагентов и продуктов до, во время и после химических реакций .

Стехиометрия основана на законе сохранения массы , согласно которому общая масса реагентов равна общей массе продуктов, что приводит к пониманию того, что отношения между количествами реагентов и продуктов обычно образуют соотношение целых положительных чисел. Это означает, что если известны количества отдельных реагентов, то можно рассчитать количество продукта. И наоборот, если количество одного реагента известно и количество продуктов можно определить эмпирически, то количество других реагентов также можно рассчитать.

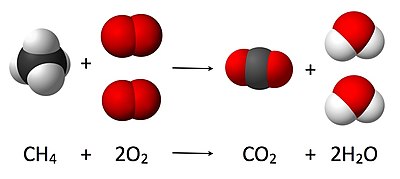
Это показано на изображении здесь, где сбалансированное уравнение:

СН ₄ + 2 О ₂ → СО ₂ + 2 Н ₂ О

Здесь одна молекула метана и реагирует с двумя молекулами газообразного кислорода с образованием одной молекулы углекислого газа двух молекул воды . Это конкретное химическое уравнение является примером полного сгорания. Стехиометрия измеряет эти количественные отношения и используется для определения количества продуктов и реагентов, которые образуются или необходимы в данной реакции. Описание количественных отношений между веществами, участвующими в химических реакциях, называется реакционной стехиометрией . В приведенном выше примере стехиометрия реакции измеряет соотношение между количествами метана и кислорода, которые реагируют с образованием углекислого газа и воды.

Определение стехиометрии ИЮПАК

Из-за хорошо известной связи молей с атомными массами соотношения, полученные с помощью стехиометрии, можно использовать для определения массовых количеств в реакции, описываемой сбалансированным уравнением. Это называется стехиометрией состава .

Газовая стехиометрия занимается реакциями с участием газов, где газы имеют известные температуру, давление и объем и могут считаться идеальными газами . Для газов соотношение объемов идеально одинаково по закону идеального газа , но массовое соотношение одной реакции должно быть рассчитано на основе молекулярных масс реагентов и продуктов. На практике из-за существования изотопов вместо этого при расчете отношения масс молярные массы используются .

Этимология

Термин «стехиометрия» был впервые использован Иеремиасом Бенджамином Рихтером первый том книги Рихтера « Anfangsgründe der Stöchyometrie oder Meßkunst chymischer Elemente» ( «Основы стехиометрии, или искусство измерения химических элементов »). в 1792 году, когда был опубликован Термин происходит от древнегреческого слова στοιχεῖον stoiheîon «элемент». и μέτρον метрон «мера».Л. Дармстедтер и Ральф Э. Оспер написали по этому поводу полезный отчет.

Определение

Основная статья: Количество вещества

Стехиометрическое количество или стехиометрическое соотношение реагента – это оптимальное количество или соотношение, при котором, предполагая , что реакция протекает до завершения:

1. Весь реагент израсходован.
2. Дефицита реагента нет.
3. Избытка реагента нет.

Стехиометрия опирается на самые основные законы, которые помогают лучше понять ее, т. е. закон сохранения массы , закон определенных пропорций (т. е. закон постоянного состава ), закон кратных пропорций и закон обратных пропорций . Вообще химические реакции соединяют в определенных соотношениях химические вещества. Поскольку химические реакции не могут ни создать, ни разрушить материю, ни превратить один элемент в другой, количество каждого элемента должно быть одинаковым на протяжении всей реакции. Например, количество атомов данного элемента X на стороне реагента должно равняться количеству атомов этого элемента на стороне продукта, независимо от того, все ли эти атомы действительно участвуют в реакции.

Химические реакции, как макроскопические единичные операции, состоят просто из очень большого числа элементарных реакций , в которых одна молекула реагирует с другой молекулой. Поскольку реагирующие молекулы (или фрагменты) состоят из определенного набора атомов в целочисленном соотношении, соотношение между реагентами в полной реакции также находится в целочисленном соотношении. В реакции может потребляться более одной молекулы, и стехиометрическое число учитывает это число, определяемое как положительное для продуктов (добавленных) и отрицательное для реагентов (удаленных). Беззнаковые коэффициенты обычно называют стехиометрическими коэффициентами .

Каждый элемент имеет атомную массу , а если рассматривать молекулы как совокупность атомов, то соединения имеют определенную молярную массу . По определению атомная масса углерода-12 равна 12 Да , что дает молярную массу 12 г/моль. Число молекул на моль в веществе определяется константой Авогадро , определяемой как 6,022 140 76 × 10. ²³ моль ⁻¹ . Таким образом, для расчета стехиометрии по массе количество молекул, необходимое для каждого реагента, выражается в молях и умножается на молярную массу каждого, чтобы получить массу каждого реагента на моль реакции. Массовые отношения можно рассчитать, разделив каждое на общее количество во всей реакции.

Элементы в их естественном состоянии представляют собой смеси изотопов различной массы; таким образом, атомные массы и, следовательно, молярные массы не являются целыми числами. Например, вместо точного соотношения 14:3 17,04 г аммиака состоят из 14,01 г азота и 3 × 1,01 г водорода, поскольку природный азот включает небольшое количество азота-15, а природный водород включает водород-2 ( дейтерий ).

Стехиометрический реагент — это реагент, который расходуется в реакции, в отличие от каталитического реагента , который не расходуется в общей реакции, поскольку он реагирует на одной стадии и регенерируется на другой стадии.

Перевод граммов в моли

Стехиометрия используется не только для балансировки химических уравнений, но также используется при преобразованиях, т. е. преобразовании граммов в моли с использованием молярной массы в качестве коэффициента преобразования или из граммов в миллилитры с использованием плотности . Например, чтобы найти количество NaCl (хлорида натрия) в 2,00 г, нужно сделать следующее:

${\frac {2.00{\mbox{ g NaCl}}}{58.44{\mbox{ g NaCl mol}}^{-1}}}=0.0342\ {\text{mol}}$

В приведенном выше примере, записанные в виде дроби, единицы граммов образуют мультипликативное тождество, которое эквивалентно единице (г/г = 1), с результирующим количеством в молях (нужная единица измерения), как показано. в следующем уравнении

$\left({\frac {2.00{\mbox{ g NaCl}}}{1}}\right)\left({\frac {1{\mbox{ mol NaCl}}}{58.44{\mbox{ g NaCl}}}}\right)=0.0342\ {\text{mol}}$

Молярная доля

Стехиометрия часто используется для балансировки химических уравнений (стехиометрия реакций). Например, два двухатомных газа, водород и кислород , могут объединиться с образованием жидкости, воды, в экзотермической реакции , как описано следующим уравнением:

2 Ч ₂ + О ₂ → 2 Ч ₂ О

Стехиометрия реакции описывает соотношение молекул водорода, кислорода и воды 2:1:2 в приведенном выше уравнении.

Молярное соотношение позволяет производить преобразование молей одного вещества в моли другого. Например, в реакции

2 СН ₃ ОН + 3 О ₂ → 2 СО ₂ + 4 Н ₂ О

количество воды, которое получится при сгорании 0,27 моля CH.
₃ OH получают, используя молярное соотношение CH
₃ ОН и Н
₂ О от 2 до 4.

$\left({\frac {0.27{\mbox{ mol }}\mathrm {CH_{3}OH} }{1}}\right)\left({\frac {4{\mbox{ mol }}\mathrm {H_{2}O} }{2{\mbox{ mol }}\mathrm {CH_{3}OH} }}\right)=0.54\ {\text{mol }}\mathrm {H_{2}O}$

Термин «стехиометрия» также часто используется для обозначения молярных пропорций элементов в стехиометрических соединениях (стехиометрия состава). Например, стехиометрия водорода и кислорода в H
₂ О составляет 2:1. В стехиометрических соединениях молярные доли представляют собой целые числа.

Определение количества продукта

Стехиометрию также можно использовать для определения количества продукта, образующегося в результате реакции. кусок твердой меди добавить Если к водному раствору нитрата серебра (Cu) ( AgNO ₃ ), серебро (Ag) будет заменено в одной реакции замещения с образованием водного нитрата меди (II) ( Cu(NO ₃ ) ₂ ) и твердое серебро. Сколько серебра получится, если к раствору избытка нитрата серебра добавить 16,00 г меди?

Будут использоваться следующие шаги:

1. Напишите и уравновесьте уравнение
2. Масса в моли: Перевести граммы меди в моли меди.
3. Молярное соотношение: конвертируйте моли Cu в моли полученного Ag.
4. Моль в массу: переведите моли Ag в граммы произведенного Ag.

Полное сбалансированное уравнение будет иметь вид:

Cu + 2 AgNO ₃ → Cu(NO ₃ ) ₂ + 2 Ag

На этапе преобразования массы в моль масса меди (16,00 г) будет преобразована в моли меди путем деления массы меди на ее молярную массу : 63,55 г/моль.

$\left({\frac {16.00{\mbox{ g Cu}}}{1}}\right)\left({\frac {1{\mbox{ mol Cu}}}{63.55{\mbox{ g Cu}}}}\right)=0.2518\ {\text{mol Cu}}$

Теперь, когда количество Cu в молях (0,2518) найдено, мы можем установить мольное соотношение. Это можно определить, взглянув на коэффициенты сбалансированного уравнения: Cu и Ag находятся в соотношении 1:2.

$\left({\frac {0.2518{\mbox{ mol Cu}}}{1}}\right)\left({\frac {2{\mbox{ mol Ag}}}{1{\mbox{ mol Cu}}}}\right)=0.5036\ {\text{mol Ag}}$

Теперь, когда известно, что количество произведенного Ag составляет 0,5036 моль, мы преобразуем это количество в граммы произведенного Ag, чтобы прийти к окончательному ответу:

$\left({\frac {0.5036{\mbox{ mol Ag}}}{1}}\right)\left({\frac {107.87{\mbox{ g Ag}}}{1{\mbox{ mol Ag}}}}\right)=54.32\ {\text{g Ag}}$

Этот набор вычислений можно свести к одному шагу:

$m_{\mathrm {Ag} }=\left({\frac {16.00{\mbox{ g }}\mathrm {Cu} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {Cu} }{63.55{\mbox{ g }}\mathrm {Cu} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {Ag} }{1{\mbox{ mol }}\mathrm {Cu} }}\right)\left({\frac {107.87{\mbox{ g }}\mathrm {Ag} }{1{\mbox{ mol Ag}}}}\right)=54.32{\mbox{ g}}$

Дальнейшие примеры

Для пропана ( C ₃ H ₈ ), реагирующий с газообразным кислородом ( O ₂ ), сбалансированное химическое уравнение:

С ₃ Н ₈ + 5 О ₂ → 3 СО ₂ + 4 Н ₂ О

Масса воды, образовавшаяся, если 120 г пропана ( C ₃ H ₈ ) сгорает в избытке кислорода, затем

$m_{\mathrm {H_{2}O} }=\left({\frac {120.{\mbox{ g }}\mathrm {C_{3}H_{8}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {C_{3}H_{8}} }{44.09{\mbox{ g }}\mathrm {C_{3}H_{8}} }}\right)\left({\frac {4{\mbox{ mol }}\mathrm {H_{2}O} }{1{\mbox{ mol }}\mathrm {C_{3}H_{8}} }}\right)\left({\frac {18.02{\mbox{ g }}\mathrm {H_{2}O} }{1{\mbox{ mol }}\mathrm {H_{2}O} }}\right)=196{\mbox{ g}}$

Стехиометрическое соотношение

Стехиометрия также используется для определения правильного количества одного реагента , чтобы «полностью» прореагировать с другим реагентом в химической реакции , то есть стехиометрических количеств, при которых не останется остатков реагентов при протекании реакции. Ниже показан пример термитной реакции .

Fe ₂ O ₃ + 2 Al → Al ₂ O ₃ + 2 Fe

Это уравнение показывает, что из 1 моля оксида железа(III) и 2 молей алюминия образуется 1 моль оксида алюминия и 2 моля железа . Итак, для полной реакции с 85,0 г оксида железа(III) (0,532 моль) необходимо 28,7 г (1,06 моль) алюминия.

$m_{\mathrm {Al} }=\left({\frac {85.0{\mbox{ g }}\mathrm {Fe_{2}O_{3}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {Fe_{2}O_{3}} }{159.7{\mbox{ g }}\mathrm {Fe_{2}O_{3}} }}\right)\left({\frac {2{\mbox{ mol Al}}}{1{\mbox{ mol }}\mathrm {Fe_{2}O_{3}} }}\right)\left({\frac {26.98{\mbox{ g Al}}}{1{\mbox{ mol Al}}}}\right)=28.7{\mbox{ g}}$

Ограничивающий реагент и процентный выход

Основные статьи: Ограничивающий реагент и выход (химия)

Лимитирующий реагент — это реагент, который ограничивает количество продукта, который может образоваться, и полностью расходуется после завершения реакции. Избыточный реагент — это реагент, который остается после остановки реакции из-за истощения лимитирующего реагента.

Рассмотрим уравнение обжига сульфида свинца(II) (PbS) в кислороде ( O ₂ ) для производства оксида свинца(II) (PbO) и диоксида серы ( СО2 _: )

2 PbS + 3 O ₂ → 2 PbO + 2 SO ₂

Определить теоретический выход оксида свинца(II), если 200,0 г сульфида свинца(II) и 200,0 г кислорода нагреть в открытом сосуде:

$m_{\mathrm {PbO} }=\left({\frac {200.0{\mbox{ g }}\mathrm {PbS} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {PbS} }{239.27{\mbox{ g }}\mathrm {PbS} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {PbO} }{2{\mbox{ mol }}\mathrm {PbS} }}\right)\left({\frac {223.2{\mbox{ g }}\mathrm {PbO} }{1{\mbox{ mol }}\mathrm {PbO} }}\right)=186.6{\mbox{ g}}$

$m_{\mathrm {PbO} }=\left({\frac {200.0{\mbox{ g }}\mathrm {O_{2}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {O_{2}} }{32.00{\mbox{ g }}\mathrm {O_{2}} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {PbO} }{3{\mbox{ mol }}\mathrm {O_{2}} }}\right)\left({\frac {223.2{\mbox{ g }}\mathrm {PbO} }{1{\mbox{ mol }}\mathrm {PbO} }}\right)=930.0{\mbox{ g}}$

Поскольку на 200,0 г PbS образуется меньшее количество PbO, ясно, что PbS является лимитирующим реагентом.

В действительности фактический выход не совпадает с теоретически рассчитанным стехиометрическим выходом. Таким образом, процентная доходность выражается следующим уравнением:

${\mbox{percent yield}}={\frac {\mbox{actual yield}}{\mbox{theoretical yield}}}$

Если получено 170,0 г оксида свинца(II), то процентный выход будет рассчитываться следующим образом:

${\mbox{percent yield}}={\frac {\mbox{170.0 g PbO}}{\mbox{186.6 g PbO}}}=91.12\%$

Пример

Рассмотрим следующую реакцию, в которой хлорид железа(III) реагирует с сероводородом с образованием сульфида железа(III) и хлористого водорода :

2 FeCl ₃ + 3 H ₂ S → Fe ₂ S ₃ + 6 HCl

Стехиометрические массы для этой реакции:

324,41 г FeCl ₃ , 102,25 г H ₂ S , 207,89 г Fe ₂ S ₃ , 218,77 г HCl

Предположим, 90,0 г FeCl ₃ реагирует с 52,0 г Ч ₂ С . Чтобы найти лимитирующий реагент и массу HCl, образующегося в результате реакции, изменим указанные выше количества в 90/324,41 раза и получим следующие количества:

90,00 г FeCl3 _{, 28,37} г H ₂ S , 57,67 г Fe ₂ S ₃ , 60,69 г HCl

Лимитирующим реагентом (или реагентом) является FeCl ₃ , так как израсходованы все 90,00 г его, а всего 28,37 г. H ₂ S расходуются. Таким образом, 52,0 − 28,4 = 23,6 г. H ₂ S осталось в избытке. Масса полученной HCl составляет 60,7 г.

Глядя на стехиометрию реакции, можно было догадаться FeCl ₃ является лимитирующим реагентом; в три раза больше FeCl ₃ используется по сравнению с H ₂ S (324 г против 102 г).

Разная стехиометрия в конкурирующих реакциях

Часто с использованием одних и тех же исходных материалов возможно проведение более чем одной реакции. Реакции могут различаться по своей стехиометрии. Например метилирование бензола , ( C ₆ H ₆ ), по реакции Фриделя–Крафтса с использованием AlCl ₃ в качестве катализатора может давать однократно метилированные ( C ₆ H ₅ CH ₃ ), дважды метилированный ( C ₆ H ₄ (CH ₃ ) ₂ ), или еще более сильно метилированный ( C ₆ H _{6− n} (CH ₃ ) _n ) продукты, как показано в следующем примере,

C ₆ H ₆ + CH ₃ Cl → C ₆ H ₅ CH ₃ + HCl

C ₆ H ₆ + 2 CH ₃ Cl → C ₆ H ₄ (CH ₃ ) ₂ + 2 HCl

C ₆ H ₆ + n CH ₃ Cl → C ₆ H _{6− n} (CH ₃ ) _n + n HCl

В этом примере то, какая реакция происходит, частично контролируется относительными концентрациями реагентов.

Стехиометрический коэффициент и стехиометрическое число

Проще говоря, стехиометрический коэффициент любого данного компонента — это количество молекул и/или формульных единиц , которые участвуют в реакции, как написано. Родственной концепцией является стехиометрическое число (с использованием номенклатуры ИЮПАК), где стехиометрический коэффициент умножается на +1 для всех продуктов и на -1 для всех реагентов.

Например, в реакции CH ₄ + 2 O ₂ → CO ₂ + 2 H ₂ O , стехиометрическое число CH ₄ равен −1, стехиометрическое число O ₂ равен −2, для CO ₂ это будет +1, а для H ₂ O это +2.

Говоря более технически точным языком, стехиометрическое число в химической реакционной системе -го компонента i определяется как

$\nu _{i}={\frac {\Delta N_{i}}{\Delta \xi }}\,$

или

$\Delta N_{i}=\nu _{i}\,\Delta \xi \,$

где $N_{i}$ - число молекул i , а $\xi$ — это переменная прогресса или степень реакции .

Стехиометрическое число $\nu _{i}$ представляет собой степень участия химического вещества в реакции. (которые расходуются) присваиваются отрицательные числа Согласно соглашению, реагентам — положительные , а продуктам , что соответствует соглашению о том, что увеличение степени реакции будет соответствовать смещению состава от реагентов к продуктам. Однако любую реакцию можно рассматривать как идущую в обратном направлении, и с этой точки зрения она изменится в отрицательном направлении, чтобы снизить свободную энергию Гиббса системы. Будет ли реакция действительно идти в произвольно выбранном прямом направлении или нет, зависит от количеств веществ, присутствующих каждый данный момент времени, что определяет кинетику и термодинамику , т. е. лежит ли равновесие справа слева или в от исходного состояния.

В механизмах реакций стехиометрические коэффициенты для каждой стадии всегда целые числа , поскольку в элементарных реакциях всегда участвуют целые молекулы. Если использовать составное представление общей реакции, некоторые из них могут быть рациональными дробями . Часто присутствуют химические соединения, которые не участвуют в реакции; поэтому их стехиометрические коэффициенты равны нулю. Любой регенерируемый химический компонент, например катализатор , также имеет стехиометрический коэффициент, равный нулю.

Самый простой случай — изомеризация.

А → Б

в котором ν _B = 1 , поскольку при каждом протекании реакции образуется одна молекула B, а ν _A = −1 , поскольку одна молекула A обязательно потребляется. В любой химической реакции сохраняется не только общая масса , но и число атомов каждого сорта , что накладывает соответствующие ограничения на возможные значения стехиометрических коэффициентов.

, обычно одновременно протекают несколько реакций В любой природной реакционной системе, в том числе в биологии . Поскольку любой химический компонент может участвовать в нескольких реакциях одновременно, стехиометрическое число i -го компонента в k -й реакции определяется как

$\nu _{ik}={\frac {\partial N_{i}}{\partial \xi _{k}}}\,$

так что общее (дифференциальное) изменение количества i -го компонента равно

$dN_{i}=\sum _{k}\nu _{ik}\,d\xi _{k}.\,$

Степень реакции обеспечивает самый ясный и явный способ представления изменения состава, хотя она еще не получила широкого распространения.

В случае сложных реакционных систем часто полезно рассматривать как представление реакционной системы в терминах количеств присутствующих химических веществ { N _i } ( переменные состояния ), так и представление в терминах фактических композиционных степеней свободы , как выражается степенью реакции { ξ _k } . Преобразование вектора , выражающего размеры, в вектор, выражающий суммы, использует прямоугольную матрицу , элементами которой являются стехиометрические числа [ ν _{i k} ] .

Максимум и минимум для любого ξ _k возникают всякий раз, когда первый из реагентов исчерпывается для прямой реакции; или первый из «продуктов» истощается, если рассматривать реакцию как идущую в обратном направлении. Это чисто кинематическое реакции ограничение на симплекс — гиперплоскость в пространстве состава или N которого -пространстве, размерность равна числу линейно-независимых химических реакций. Это обязательно меньше числа химических компонентов, поскольку каждая реакция проявляет связь по крайней мере между двумя химическими веществами. Доступная область гиперплоскости зависит от количества реально присутствующих каждого химического вещества, что является случайным фактом. Разные такие количества могут даже порождать разные гиперплоскости, имеющие одну и ту же алгебраическую стехиометрию.

В соответствии с принципами химической кинетики и термодинамического равновесия каждая химическая реакция обратима , по крайней мере до некоторой степени, так что каждая точка равновесия должна быть внутренней точкой симплекса. Как следствие, экстремумы для ξ s не возникнут, если экспериментальная система не будет приготовлена ​​с нулевыми начальными количествами некоторых продуктов.

Число физически независимых реакций может быть даже больше, чем число химических компонентов, и зависит от различных механизмов реакции. Например, может существовать два (или более) пути реакции для указанной выше изомерии. Реакция может протекать сама по себе, но быстрее и с другими интермедиатами, в присутствии катализатора.

(Безразмерными) «единицами» можно считать молекулы или моли . Чаще всего используются «кроты», но более убедительно представлять дополнительные химические реакции в терминах молекул. N константу s и ξ s преобразуются в мольные единицы путем деления на Авогадро . Хотя можно использовать размерные единицы массы , комментарии о целых числах больше не применимы.

Матрица стехиометрии

Основная статья: Теория сетей химических реакций

В сложных реакциях стехиометрии часто представляются в более компактной форме, называемой матрицей стехиометрии. обозначается символом N. Матрица стехиометрии

Если в реакционной сети есть n реакций и m участвующих видов молекул, то матрица стехиометрии будет иметь соответственно m строк и n столбцов.

Например, рассмотрим систему реакций, показанную ниже:

С ₁ → С ₂

5С3 + _С2 4С3 ₊ 2С2 _→

С3 → _С4

С ₄ → С ₅

Эта система включает четыре реакции и пять различных видов молекул. Матрицу стехиометрии этой системы можно записать в виде:

$\mathbf {N} ={\begin{bmatrix}-1&0&0&0\\1&1&0&0\\0&-1&-1&0\\0&0&1&-1\\0&0&0&1\\\end{bmatrix}}$

где строки соответствуют S1 _​ , _S2 , _S3 , _S4 и _S5 . соответственно Процесс преобразования схемы реакции в матрицу стехиометрии может представлять собой преобразование с потерями: например, стехиометрии во второй реакции упрощаются при включении в матрицу. Это означает, что не всегда возможно восстановить исходную схему реакции по матрице стехиометрии.

Часто матрица стехиометрии объединяется с вектором скорости v и вектором вида x , чтобы сформировать компактное уравнение, уравнение биохимической системы , описывающее скорость изменения молекулярных видов:

${\frac {d\mathbf {x} }{dt}}=\mathbf {N} \cdot \mathbf {v} .$

Газовая стехиометрия

Газовая стехиометрия — это количественная связь (соотношение) между реагентами и продуктами в химической реакции с реакциями, в результате которых образуются газы . Газовая стехиометрия применяется, когда образующиеся газы считаются идеальными , а температура, давление и объем газов известны. Для этих расчетов используется закон идеального газа. Часто, но не всегда, стандартные температура и давление (STP) принимаются равными 0 °C и 1 бар и используются в качестве условий для стехиометрических расчетов газа.

Расчеты газовой стехиометрии позволяют определить неизвестный объем или массу газообразного продукта или реагента. Например, если мы хотим вычислить объем газообразного NO ₂ образуется при сгорании 100 г NH ₃ , по реакции:

4 NH ₃ (г) + 7 O ₂ (г) → 4 NO ₂ (г) + 6 H ₂ O (ж)

мы проведем следующие расчеты:

$100\,\mathrm {g\,NH_{3}} \cdot {\frac {1\,\mathrm {mol\,NH_{3}} }{17.034\,\mathrm {g\,NH_{3}} }}=5.871\,\mathrm {mol\,NH_{3}}$

Существует молярное соотношение 1:1 NH ₃ до NO ₂ в вышеуказанной реакции сбалансированного горения, поэтому 5,871 моль NO ₂ образуется. Мы будем использовать закон идеального газа для определения объема при 0 °C (273,15 К) и 1 атмосфере, используя газового закона R константу = 0,08206 л·атм·К. ⁻¹ ·моль ⁻¹ :

${\begin{aligned}PV&=nRT\\V&={\frac {nRT}{P}}\\&={\frac {5.871\cdot 0.08206\cdot 273.15}{1}}\\&=131.597\,\mathrm {L\,NO_{2}} \end{aligned}}$

Газовая стехиометрия часто предполагает знание молярной массы газа с учетом плотности этого газа. Закон идеального газа можно переформулировать, чтобы получить связь между плотностью и молярной массой идеального газа:

$\rho ={\frac {m}{V}}$ и $n={\frac {m}{M}}$

и таким образом:

$\rho ={\frac {MP}{R\,T}}$

где:

• P = абсолютное давление газа
• V  = gas volume
• n = количество (измеряется в молях )
• R = универсальная константа закона идеального газа
• T = абсолютная температура газа
• ρ = плотность газа при T и P
• м = масса газа
• M = молярная масса газа

Стехиометрические соотношения воздух-топливо обычных видов топлива

См. Также: Соотношение воздух-топливо и сгорание.

В реакции горения кислород вступает в реакцию с топливом, и точка, в которой расходуется ровно весь кислород и сгорает все топливо, определяется как стехиометрическая точка. При большем количестве кислорода (сверхстехиометрическое горение) часть его остается непрореагировавшей. Аналогично, если сгорание неполное из-за отсутствия достаточного количества кислорода, топливо остается непрореагировавшим. (Непрореагировавшее топливо также может остаться из-за медленного сгорания или недостаточного смешивания топлива и кислорода – это не связано со стехиометрией.) Различные углеводородные топлива имеют разное содержание углерода, водорода и других элементов, поэтому их стехиометрия различается.

Кислород составляет всего 20,95% объема воздуха и всего 23,20% его массы. Перечисленные ниже соотношения воздух-топливо намного превышают эквивалентные соотношения кислород-топливо из-за высокой доли инертных газов в воздухе.

Топливо	Соотношение по массе	Соотношение по объему	Процент топлива по массе	Основная реакция
Бензин	14.7 : 1	—	6.8%	2 С 8 Н 18 + 25 О 2 → 16 СО 2 + 18 Н 2 О
Природный газ	17.2 : 1	9.7  : 1	5.8%	СН 4 + 2 О 2 → СО 2 + 2 Н 2 О
Пропан ( LP )	15.67 : 1	23.9 : 1	6.45%	С 3 Н 8 + 5 О 2 → 3 СО 2 + 4 Н 2 О
Этанол	9 : 1	—	11.1%	С 2 Н 6 О + 3 О 2 → 2 СО 2 + 3 Н 2 О
Метанол	6.47 : 1	—	15.6%	2 СН 4 О + 3 О 2 → 2 СО 2 + 4 Н 2 О
н -бутанол	11.2 : 1	—	8.2%	С 4 Н 10 О + 6 О 2 → 4 СО 2 + 5 Н 2 О
Водород	34.3 : 1	2.39 : 1	2.9%	2 Ч 2 + О 2 → 2 Ч 2 О
Дизель	14.5 : 1	—	6.8%	2 С 12 Н 26 + 37 О 2 → 24 СО 2 + 26 Н 2 О
Метан	17.19 : 1	9.52 : 1	5.5%	СН 4 + 2 О 2 → СО 2 + 2 Н 2 О
Ацетилен	13.26 : 1	11.92 : 1	7.0%	2 С 2 Н 2 + 5 О 2 → 4 СО 2 + 2 Н 2 О
Этан	16.07 : 1	16.68 : 1	5.9%	2 С 2 Н 6 + 7 О 2 → 4 СО 2 + 6 Н 2 О
Бутан	15.44 : 1	30.98 : 1	6.1%	2 С 4 Н 10 + 13 О 2 → 8 СО 2 + 10 Н 2 О
Пентан	15.31 : 1	38.13 : 1	6.1%	С 5 Н 12 + 8 О 2 → 5 СО 2 + 6 Н 2 О

Бензиновые двигатели могут работать при стехиометрическом соотношении воздух-топливо, поскольку бензин довольно летуч и перед воспламенением смешивается (распыляется или карбюрируется) с воздухом. Дизельные двигатели, напротив, работают на бедной смеси, имея больше воздуха, чем требует простая стехиометрия. Дизельное топливо менее летучее и эффективно сгорает при впрыскивании.

См. также

• Нестехиометрическое соединение
• Уравнение биохимических систем
• Химическая реакция
• Химическое уравнение
• Молекула
• Молярная масса
• Закон идеального газа

Ссылки

• Зумдал, Стивен С. Химические принципы . Хоутон Миффлин, Нью-Йорк, 2005 г., стр. 148–150.
• Основы двигателей внутреннего сгорания, Джон Б. Хейвуд

Внешние ссылки

• Праймер по сгоранию двигателя от Плимутского университета.
• Бесплатные учебные пособия по стехиометрии от ChemCollective Карнеги-Меллона
• Надстройка стехиометрии для Microsoft Excel. Архивировано 11 мая 2011 г. на Wayback Machine для расчета молекулярных масс, коэффициентов реакции и стехиометрии.
• Калькулятор стехиометрии реакций — комплексный бесплатный онлайн-калькулятор стехиометрии реакций.