Усеченный куб

Усеченный кубический граф
Усеченный кубический граф
	4-кратной симметрии Диаграмма Шлегеля
Вершины	24
Края	36
Автоморфизм	48
Хроматическое число	3
Характеристики	Кубический , гамильтонов , регулярный , нуль-симметричный
	Таблица графиков и параметров

Усеченный куб
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Архимедово тело Однородный многогранник
Элементы	F = 14, E = 36, V = 24 (χ = 2)
Лица по сторонам	8{3}+6{8}
Обозначение Конвея	ТК
Символы Шлефли	т{4,3}
Символы Шлефли	т _0,1 {4,3}
Символ Витхоффа	2 3 \| 4
Диаграмма Кокстера
Группа симметрии	О _h , B ₃ , [4,3], (*432), порядок 48
Группа вращения	О , [4,3] ⁺, (432), порядок 24
Двугранный угол	3-8: 125°15′51″ 8-8: 90°
Ссылки	У ₀₉ , С ₂₁ , Ж ₈
Характеристики	Полуправильный выпуклый
Цветные лица	3.8.8 ( фигура вершины )
Октаэдр Триакиса ( двойной многогранник )	Сеть

В геометрии , усеченный куб или усеченный шестигранник , представляет собой архимедово тело . Он имеет 14 правильных граней (6 восьмиугольных и 8 треугольных ), 36 ребер и 24 вершины.

Если усеченный куб имеет единичную длину ребра, его двойственный триаки-октаэдр имеет ребра длиной 2 и 2 + √ 2 .

Площадь и объем

Площадь A и объем V усеченного куба с длиной ребра a равны:

{\begin{aligned}A&=2\left(6+6{\sqrt {2}}+{\sqrt {3}}\right)a^{2}&&\approx 32.434\,6644a^{2}\\V&={\frac {21+14{\sqrt {2}}}{3}}a^{3}&&\approx 13.599\,6633a^{3}.\end{aligned}}

Ортогональные проекции

Усеченный куб имеет пять специальных ортогональных проекций , центрированных на вершине, на двух типах ребер и двух типах граней: треугольниках и восьмиугольниках. Последние два соответствуют _{B 2} и A ₂ плоскостям Кокстера .

Ортогональные проекции
В центре	Вертекс	Край 3-8	Край 8-8	Лицо Октагон	Лицо Треугольник
Твердый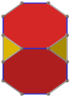
Каркас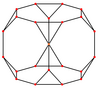
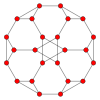
Двойной
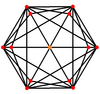
Проективный симметрия	[2]	[2]	[2]	[4]	[6]

Сферическая черепица

Усеченный куб также можно представить в виде сферической мозаики и спроецировать на плоскость с помощью стереографической проекции . Эта проекция является равноугольной , сохраняющей углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.

Ортографическая проекция	Стереографические проекции
	восьмиугольник с центром	треугольник с центром

Декартовы координаты

Декартовы координаты вершин усеченного шестигранника с центром в начале координат и длиной ребра 2 ξ — это все перестановки

(± ξ , ±1, ±1),

где ξ = √ 2 − 1.

Параметр ξ можно изменять в пределах ±1. Значение 1 дает куб , 0 — кубооктаэдр , а отрицательные значения — самопересекающиеся октаграммные грани.

Если самопересекающиеся части октаграмм удалить, оставив квадраты и усекая треугольники в шестиугольники, образуются усеченные октаэдры , и последовательность заканчивается тем, что центральные квадраты сводятся к точке и образуют октаэдр .

Диссекция

Усеченный куб можно разрезать на центральный куб с шестью квадратными куполами вокруг каждой грани куба и 8 правильными тетраэдрами по углам. Это рассечение также можно увидеть в рунических кубических сотах с ячейками куба , тетраэдра и ромбокубооктаэдра .

Это рассечение можно использовать для создания тороида Стюарта со всеми правильными гранями, удалив два квадратных купола и центральный куб. Этот раскопанный куб имеет 16 треугольников , 12 квадратов и 4 восьмиугольника . ^{[ 1 ]}^{[ 2 ]}

Расположение вершин

Он разделяет расположение вершин с тремя невыпуклыми однородными многогранниками :

Усеченный куб	Невыпуклый большой ромбокубооктаэдр	Большой кубический октаэдр	Большой ромбогексаэдр

Связанные многогранники

Усеченный куб связан с другими многогранниками и мозаиками по симметрии.

Усечённый куб — один из семейства однородных многогранников, родственных кубу и правильному октаэдру.

Однородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Мутации симметрии

Этот многогранник топологически связан как часть последовательности однородных усеченных многогранников с конфигурациями вершин (3,2 n .2 n ) и [ n ,3 ] симметрией группы Кокстера , а также серии многогранников и мозаик n .8.8.

* n 32 мутация симметрии усеченных сферических мозаик: t{ n ,3}
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.
Symmetry *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Truncated figures
Symbol	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}
Triakis figures
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

* n 42 мутация симметрии усеченных мозаик: n.8.8 v т и
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracompact
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
n-kis figures
Config.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

Попеременное усечение

Тетраэдр, усечение его ребра и усеченный куб

Усечение чередующихся вершин куба дает тетраэдр с фаской , то есть усечение ребра тетраэдра.

Усеченный треугольный трапецоэдр — это еще один многогранник, который можно образовать путем усечения ребер куба.

Связанные многогранники

Усеченный является вторым в куб последовательности усеченных гиперкубов :

Усеченные гиперкубы
Изображение								...
Имя	Октагон	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Усеченный 7-куб	Усеченный 8-куб
Диаграмма Кокстера
Вершинная фигура	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3,3}	( )v{3,3,3,3,3}

Усеченный кубический граф

В математической области теории графов усеченный кубический граф — это граф вершин и ребер усеченного куба , одного из архимедовых тел . Он имеет 24 вершины и 36 ребер и представляет собой кубический архимедовый граф . ^{[ 3 ]}

орфографический

См. также

Вращающийся усеченный куб
Кубосвязные циклы — семейство графов, включающее скелет усеченного куба.

Ссылки

^ Б. М. Стюарт, Приключения среди тороидов (1970) ISBN 978-0-686-11936-4
^ «Приключения среди тороидов - Глава 5 - Простейшие (R)(A)(Q)(T) тороиды рода p=1» .
^ Читай, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Кромвель, П. Многогранники , CUP hbk (1997), pbk. (1999). Гл.2 стр. 79-86 Архимедовы тела

Внешние ссылки

Вайсштейн, Эрик В. , « Усеченный куб » (« Архимедово тело ») в MathWorld .
- Вайсштейн, Эрик В. «Усеченный кубический граф» . Математический мир .
Клитцинг, Ричард. «3D выпуклые однородные многогранники o3x4x — тик» .
Редактируемая для печати сеть усеченного куба с интерактивным 3D-видом
Однородные многогранники
Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- VRML Модель
- Обозначение Конвея для многогранников. Попробуйте: «tC».

[1] Б. М. Стюарт, Приключения среди тороидов (1970) ISBN 978-0-686-11936-4

[2] «Приключения среди тороидов - Глава 5 - Простейшие (R)(A)(Q)(T) тороиды рода p=1» .

[3] Читай, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269

[ 1 ]

[ 2 ]

[ 3 ]