Теория многогранных скелетных электронных пар
В химии теория многогранных скелетных электронных пар (PSEPT) предоставляет правила счета электронов, полезные для предсказания структуры кластеров, таких как борановые и карборановые кластеры. Правила счета электронов были первоначально сформулированы Кеннетом Уэйдом . [1] и были далее развиты другими, включая Майкла Мингоса ; [2] их иногда называют правилами Уэйда или правилами Уэйда-Мингоса . [3] Правила основаны на молекулярно-орбитальном подходе к связи. [4] [5] [6] [7] Эти правила были расширены и унифицированы в форме Джеммиса мно правил . [8] [9]
Прогнозирование структуры кластерных соединений
[ редактировать ]
Различные правила (4 n , 5 n или 6 n ) применяются в зависимости от количества электронов на вершину.
Правила 4 n достаточно точны в предсказании структуры кластеров, имеющих около 4 электронов на вершину, как это имеет место для многих боранов и карборанов . Для таких кластеров структуры основаны на дельтаэдрах , которые представляют собой многогранники , в которых каждая грань треугольна. Кластеры из 4 n классифицируются как клозо- , нидо- , арахно- или гипо- , в зависимости от того, представляют ли они полный ( клозо- ) дельтаэдр или дельтаэдр, в котором отсутствует один ( нидо- ), два ( арахно- ) или дельтаэдр. три ( гифо- ) вершины.
Однако гифокластеры встречаются относительно редко из-за того, что количество электронов достаточно велико, чтобы начать заполнять разрыхляющие орбитали и дестабилизировать структуру 4 n . Если количество электронов близко к 5 электронам на вершину, структура часто меняется на структуру, подчиняющуюся правилам 5n, основанным на 3-связных многогранниках.
По мере дальнейшего увеличения количества электронов структуры кластеров с числом электронов 5n становятся нестабильными, поэтому 6 n могут быть реализованы правила . Кластеры размером 6 n имеют структуры, основанные на кольцах.
Метод молекулярных орбиталей может быть использован для рационализации связывания кластерных соединений типов 4 n , 5 n и 6 n .
4 n правил
[ редактировать ]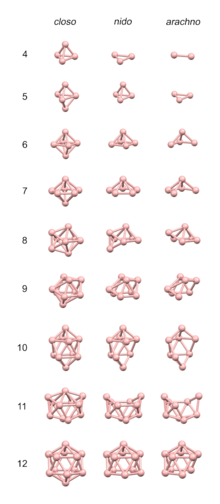
Следующие многогранники являются закрытыми многогранниками и являются основой правил 4 n ; у каждого из них треугольные грани. [10] Количество вершин в кластере определяет, на каком многограннике основана структура.
| Количество вершин | Многогранник |
|---|---|
| 4 | Тетраэдр |
| 5 | Треугольная бипирамида |
| 6 | Октаэдр |
| 7 | Пятиугольная бипирамида |
| 8 | D 2d (тригональный) додекаэдр ( взносый дисфеноид ) |
| 9 | Треугольная призма с тремя вершинами |
| 10 | Двуглавая квадратная антипризматическая молекулярная геометрия |
| 11 | Икосаэдр со суженным ребром (октадекаэдр) |
| 12 | Икосаэдр (двуглавая пятиугольная антипризма) |
Используя подсчет электронов, можно найти предсказанную структуру. n — количество вершин в кластере. Правила 4 n перечислены в следующей таблице.
| Количество электронов | Имя | Прогнозируемая структура |
|---|---|---|
| 4 n − 2 | закрытие Двуглавое | многогранник с n - 2 вершинами Закрытый и двумя закрытыми ( дополненными ) гранями |
| 4 n | закрыто | n - 1 вершина закрытого многогранника с 1 гранью, закрытой |
| 4 n + 2 | близко | замкнутый многогранник с n вершинами |
| 4 n + 4 | нидо | n + 1 замкнутый многогранник с 1 недостающей вершиной |
| 4n + 6 | арахно | многогранник с n + 2 вершинами Закрытый и двумя недостающими вершинами |
| 4n + 8 | гиф | многогранник с n + 3 вершинами Закрытый и 3 недостающими вершинами |
| 4n + 10 | клада | многогранник с n + 4 вершинами Закрытый и 4 недостающими вершинами |
10
количество валентных электронов При подсчете электронов для каждого кластера подсчитывается . Для каждого присутствующего переходного металла из общего количества электронов вычитается 10 электронов. Например, в Rh 6 (CO) 16 общее число электронов будет 6 × 9 + 16 × 2 − 6 × 10 = 86 – 60 = 26. Следовательно, кластер представляет собой замкнутый многогранник, поскольку n = 6 с 4 п + 2 = 26 .

4
При прогнозировании структуры кластеров можно учитывать и другие правила:
- Для кластеров, состоящих в основном из переходных металлов, любые присутствующие элементы основной группы часто лучше всего считать лигандами или межузельными атомами, а не вершинами.
- Более крупные и более электроположительные атомы имеют тенденцию занимать вершины с высокой связностью, а меньшие, более электроотрицательные атомы имеют тенденцию занимать вершины с низкой связностью.
- В частном случае кластеров гидрида бора каждый атом бора, соединенный с 3 или более вершинами, имеет один концевой гидрид, а атом бора, соединенный с двумя другими вершинами, имеет два концевых атома водорода. Если присутствует больше атомов водорода, они помещаются в открытые грани, чтобы выровнять координационное число вершин.
- В частном случае кластеров переходных металлов лиганды к металлическим центрам добавляются водорода, , чтобы придать металлам разумные координационные числа, и, если присутствуют какие-либо атомы они помещаются в мостиковые положения, чтобы выровнять координационные числа вершин.
В общем, закрытые структуры с n вершинами представляют собой n -вершинные многогранники.
Чтобы предсказать структуру нидо -кластера, клозо- кластер с n в качестве отправной точки используется + 1 вершиной; если кластер состоит из маленьких атомов, удаляется вершина с высокой связностью, а если кластер состоит из больших атомов, удаляется вершина с низкой связностью.
Чтобы предсказать структуру арахно- кластера, закрытый многогранник с n в качестве отправной точки используется с n + 1 вершиной + 2 вершинами, а нидокомплекс генерируется в соответствии с приведенным выше правилом; вторая вершина, смежная с первой, удаляется, если кластер состоит преимущественно из мелких атомов, вторая вершина, не смежная с первой, удаляется, если кластер состоит преимущественно из крупных атомов.
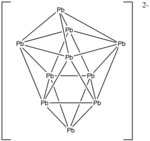
Пример: Пб 2−
10
- Количество электронов: 10 × Pb + 2 (для отрицательного заряда) = 10 × 4 + 2 = 42 электрона.
- Поскольку n = 10, 4 n + 2 = 42, кластер представляет собой близкую двуглавую квадратную антипризму.
Пример: С 2+
4
- Количество электронов: 4 × S – 2 (для положительного заряда) = 4 × 6 – 2 = 22 электрона.
- Поскольку n = 4, 4 n + 6 = 22, то кластер арахно .
- Начиная с октаэдра удаляется вершина высокой связности, а затем удаляется несмежная вершина.
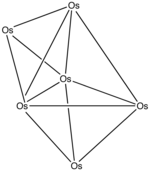
Пример: Ос 6 (СО) 18
- Количество электронов: 6 × Os + 18 × CO – 60 (для 6 атомов осмия) = 6 × 8 + 18 × 2 – 60 = 24
- Так как n = 6, 4 n = 24, кластер ограничен почти .
- Начиная с тригональной бипирамиды, грань закрывается. Карбонилы опущены для ясности.
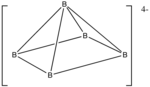
55Ч 4−
5 , атомы водорода опущены
Пример: [11] Б
55Ч 4−
5
- Количество электронов: 5 × B + 5 × H + 4 (для отрицательного заряда) = 5 × 3 + 5 × 1 + 4 = 24.
- Поскольку n = 5, 4 n + 4 = 24, то кластер является нидо.
- Начиная с октаэдра, удаляется одна из вершин.
Правила полезны также для предсказания структуры карборанов .Пример: C 2 B 7 H 13
- Количество электронов = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42
- Поскольку n в данном случае равно 9, 4 n + 6 = 42, то кластер арахно .
Учет дельтаэдрических кластеров иногда ведется путем подсчета скелетных электронов вместо общего числа электронов. Скелетные орбитали (электронные пары) и количество скелетных электронов для четырех типов дельтаэдрических кластеров:
- n -закрытие вершины : n + 1 скелетные орбитали, 2 n + 2 скелетных электрона.
- n -вершина nido : n + 2 скелетных орбитали, 2 n + 4 скелетных электрона.
- n -вершина арахно : n + 3 скелетных орбиталей, 2 n + 6 скелетных электронов.
- n -вершинная гиф : n + 4 скелетных орбитали, 2 n + 8 скелетных электронов.
Количество скелетных электронов определяется путем суммирования следующего количества электронов:
- 2 от каждого блока BH
- 3 от каждого блока ЦО
- 1 от каждого дополнительного атома водорода (сверх атомов на единицах BH и CH)
- анионный заряд электронов
5 n правил
[ редактировать ]Как обсуждалось ранее, правило 4 n в основном касается кластеров с числом электронов 4 n + k , в которых примерно по 4 электрона находятся в каждой вершине. По мере того, как на каждую вершину добавляется больше электронов, количество электронов на вершину приближается к 5. Вместо того, чтобы принимать структуры, основанные на дельтаэдрах, кластеры 5n-типа имеют структуры, основанные на другой серии многогранников, известных как 3-связные многогранники , в которых каждая вершина соединена с тремя другими вершинами. Трехсвязные многогранники являются двойственными дельтаэдрам. Ниже перечислены распространенные типы трехсвязных многогранников.

| Количество вершин | Тип 3-связного многогранника |
|---|---|
| 4 | Тетраэдр |
| 6 | Треугольная призма |
| 8 | Куб |
| 10 | Пятиугольная призма |
| 12 | D 2d псевдооктаэдр (двойной курносому дисфеноиду) |
| 14 | Двойная триаугментированная треугольная призма ( К 5 ассоциэдр ) |
| 16 | Квадратный усеченный трапецоэдр |
| 18 | Двойной икосаэдр со суженными ребрами |
| 20 | Додекаэдр |
5n Правила заключаются в следующем.
| Общее количество электронов | Прогнозируемая структура |
|---|---|
| 5 н | n -вершинный 3-связный многогранник |
| 5 н + 1 | n – 1 вершинный 3-связный многогранник с одной вершиной, вставленной в ребро |
| 5 н + 2 | n – 2-вершинный 3-связный многогранник с двумя вершинами, вставленными в ребра |
| 5н + к | n - k вершинный 3-связный многогранник с k вершинами, вставленными в ребра |
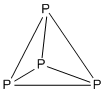
Пример: П 4
- Количество электронов: 4 × P = 4 × 5 = 20.
- Это структура из 5 n с n = 4, поэтому она тетраэдрическая.
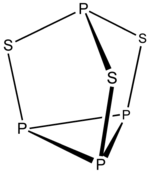
Пример: П 4 С 3
- Количество электронов 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38
- Это структура 5 n + 3 с n = 7. В ребра вставлены три вершины.
Пример: P 4 O 6
- Количество электронов 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56
- Это структура 5 n + 6 с n = 10. Шесть вершин вставлены в ребра.
6 правил
[ редактировать ]добавляется больше электронов По мере того, как в кластер 5 n , количество электронов на вершину приближается к 6. Вместо принятия структур, основанных на правилах 4 n или 5 n , кластеры, как правило, имеют структуры, управляемые правилами 6 n , которые основаны на кольца. Правила для 6 n структур следующие.
| Общее количество электронов | Прогнозируемая структура |
|---|---|
| 6 н – к | n -членное кольцо с k ⁄ 2 трансаннулярных связей |
| 6 н – 4 | n -членное кольцо с двумя трансаннулярными связями |
| 6 н – 2 | n -членное кольцо с 1 трансаннулярной связью |
| 6 н | n- членное кольцо |
| 6 н + 2 | n -членная цепь ( n- членное кольцо с 1 разорванной связью) |
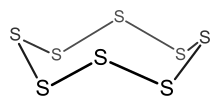
Пример: С 8
- Количество электронов = 8 × S = 8 × 6 = 48 электронов.
- Поскольку n = 8, 6 n = 48, то кластер представляет собой 8-членное кольцо.

Гексан (C 6 H 14 )
- Количество электронов = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38
- Поскольку n = 6, 6 n = 36 и 6 n + 2 = 38, то кластер представляет собой 6-членную цепь.
Изолобальные вершинные единицы
[ редактировать ]Если вершинная единица изолобальна BH, то она, по крайней мере, в принципе, может быть заменена единицей BH, даже если BH и CH не изоэлектронны. СН + единица изолобальна, следовательно, правила применимы к карборанам. Это можно объяснить пограничной орбитальной обработкой. [10] Кроме того, существуют изолобальные звенья переходных металлов. Например, Fe(CO) 3 дает 2 электрона. Вывод вкратце выглядит следующим образом:
- Fe имеет 8 валентных электронов.
- Каждая карбонильная группа является чистым донором двух электронов с внутренних σ- и π-связей , образующих 14 электронов. учетом
- Считается, что 3 пары участвуют в σ-связывании Fe-CO , а 3 пары участвуют в π -связывании от Fe к CO, уменьшая 14 до 2.
Связывание в кластерных соединениях
[ редактировать ]- близко - Б
66Ч 2−
6
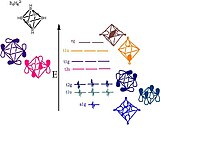
66Ч 2−
6 показаны орбитали, ответственные за формирование кластера. Показаны графические изображения орбиталей; каждый из наборов МО симметрии T и E будет иметь два или одно дополнительное графическое изображение соответственно, которые здесь не показаны.
- Атомы бора лежат в каждой вершине октаэдра и находятся в sp-гибридизации. [11] Один sp-гибрид отходит от структуры, образуя связь с атомом водорода. Другой sp-гибрид расходится в центр структуры, образуя большую связывающую молекулярную орбиталь в центре кластера. Остальные две негибридизированные орбитали лежат вдоль касательной сферической структуры, создавая больше связывающих и разрыхляющих орбиталей между вершинами бора. [9] Орбитальная диаграмма выглядит следующим образом:
- 18 каркасных молекулярных орбиталей (МО), полученных из 18 атомных орбиталей бора:
- 1 связывающая МО в центре кластера и 5 разрыхляющих МО с 6 sp-радиальных гибридных орбиталей.
- 6 связывающих МО и 6 разрыхляющих МО из 12 тангенциальных p-орбиталей.
- 18 каркасных молекулярных орбиталей (МО), полученных из 18 атомных орбиталей бора:
- Таким образом, общее количество скелетных связывающих орбиталей равно 7, т.е. n + 1 .
Кластеры переходных металлов
[ редактировать ]Кластеры переходных металлов используют d-орбитали для связи . Таким образом, они имеют до девяти связывающих орбиталей вместо четырех, присутствующих в кластерах бора и основной группы. [12] [13] PSEPT также применяется к металлоборанам.
Кластеры с межузельными атомами
[ редактировать ]Из-за большого радиуса переходные металлы обычно образуют кластеры, которые больше, чем элементы основной группы. Следствием увеличенного размера является то, что эти кластеры часто содержат атомы в своих центрах. Ярким примером является [Fe 6 C(CO) 16 ] 2- . В таких случаях правила счета электронов предполагают, что междоузельный атом вносит все валентные электроны в кластерную связь. Таким образом, [Fe 6 C(CO) 16 ] 2- эквивалентно [Fe 6 (CO) 16 ] 6- или [Fe 6 (CO) 18 ] 2- . [14]
Ссылки
[ редактировать ]- ^ Уэйд, К. (1971). «Структурное значение количества скелетных электронных пар в карборанах, высших боранах и боран-анионах, а также различных карбонильных кластерных соединениях переходных металлов». Дж. Хим. Соц. Д. 1971 (15): 792–793. дои : 10.1039/C29710000792 .
- ^ Мингос, DMP (1972). «Общая теория кластерных и кольцевых соединений основной группы и переходных элементов». Природа Физика . 236 (68): 99–102. Бибкод : 1972НПфС..236...99М . дои : 10.1038/physci236099a0 .
- ^ Уэлч, Алан Дж. (2013). «Значение и влияние правил Уэйда». хим. Коммун . 49 (35): 3615–3616. дои : 10.1039/C3CC00069A . ПМИД 23535980 .
- ^ Уэйд, К. (1976). «Структурные закономерности и закономерности связей в кластерной химии». Адв. Неорг. хим. Радиохим . Достижения неорганической химии и радиохимии. 18 : 1–66. дои : 10.1016/S0065-2792(08)60027-8 . ISBN 9780120236183 .
- ^ Джиролами, Г. (осень 2008 г.). «Конспекты лекций, распространенные в Университете Иллинойса, Урбана-Шампейн».
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) Эти заметки содержали оригинальный материал, послуживший основой разделов о правилах 4 n , 5 n и 6 n . - ^ Гилспи, Р.Дж. (1979). «Лекции памяти Нихольма». хим. Соц. Откр. 8 (3): 315–352. дои : 10.1039/CS9790800315 .
- ^ Мингос, DMP (1984). «Подход к многогранным скелетным электронным парам». Акк. хим. Рез. 17 (9): 311–319. дои : 10.1021/ar00105a003 .
- ^ Джеммис, Элуватингал Д.; Балакришнараджан, Мусири М.; Панчаратна, Паттат Д. (2001). «Объединяющее правило подсчета электронов для макрополиэдрических боранов, металлоборанов и металлоценов». Дж. Ам. хим. Соц. 123 (18): 4313–4323. дои : 10.1021/ja003233z . ПМИД 11457198 .
- ^ Перейти обратно: а б Джеммис, Элуватингал Д.; Балакришнараджан, Мусири М.; Панчаратна, Паттат Д. (2002). «Электронные требования к макрополиэдрическим боранам». хим. Преподобный. 102 (1): 93–144. дои : 10.1021/cr990356x . ПМИД 11782130 .
- ^ Перейти обратно: а б Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Передовая неорганическая химия (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5
- ^ Перейти обратно: а б Коттон, Альберт (1990). Химические приложения теории групп . Джон Уайли и сыновья. стр. 205–251 . ISBN 0-471-51094-7 .
- ^ Кинг, РБ; Рувре, Д.Х. (1977). «Химические приложения теории групп и топологии. 7. Теоретико-графовая интерпретация топологии связи в многогранных боранах, карборанах и металлических кластерах». Дж. Ам. хим. Соц. 99 (24): 7834–7840. дои : 10.1021/ja00466a014 .
- ^ Костикова, Г.П.; Корольков, Д.В. (1985). «Электронная структура кластерных комплексов переходных металлов с лигандами слабого и сильного поля». Расс. хим. Преподобный . 54 (4): 591–619. Бибкод : 1985RuCRv..54..344K . дои : 10.1070/RC1985v054n04ABEH003040 . S2CID 250797537 .
- ^ Фельнер, Томас П. (2006). «Кластерные соединения: металлоорганические соединения, содержащие переходные металлы и элементы основной группы». Энциклопедия неорганической химии . дои : 10.1002/0470862106.ia097 . ISBN 0470860782 .
Общие ссылки
[ редактировать ]- Гринвуд, Норман Н .; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8 .
- Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Передовая неорганическая химия (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5