Базовый номер репродукции

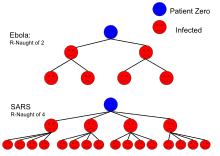
В эпидемиологии базовое репродуктивное число , или базовое репродуктивное число (иногда называемое базовым коэффициентом воспроизводства или базовым коэффициентом воспроизводства ), обозначается $R_{0}$ (произносится как R нуль или R ноль ), ^{[ 1 ]} инфекции случаев , – это ожидаемое число непосредственно вызванных одним случаем в популяции, где все люди восприимчивы к инфекции. ^{[ 2 ]} Определение предполагает, что другие люди не инфицированы и не иммунизированы (естественным путем или посредством вакцинации ). Некоторые определения, например определение Министерства здравоохранения Австралии , добавляют отсутствие «любого преднамеренного вмешательства в передачу болезней». ^{[ 3 ]} Базовое число воспроизведений не обязательно совпадает с эффективным числом воспроизведений. $R$ (обычно пишется $R_{t}$ [ t для времени], иногда $R_{e}$ ), ^{[ 4 ]} это количество случаев, возникших в текущем состоянии популяции, которое не обязательно должно быть незараженным. $R_{0}$ представляет собой безразмерное число (количество инфицированных на одного заразившегося), а не показатель времени, который имел бы единицы времени ⁻¹, ^{[ 5 ]} или единицы времени, такие как удвоение времени . ^{[ 6 ]}

$R_{0}$ не является биологической константой для патогена, поскольку на него также влияют другие факторы, такие как условия окружающей среды и поведение инфицированного населения. $R_{0}$ значения обычно оцениваются на основе математических моделей, а оценочные значения зависят от используемой модели и значений других параметров. Таким образом, значения, приведенные в литературе, имеют смысл только в данном контексте, и не рекомендуется сравнивать значения, основанные на разных моделях. ^{[ 7 ]} $R_{0}$ Сам по себе он не дает оценки того, насколько быстро инфекция распространяется среди населения.

Наиболее важные варианты использования $R_{0}$ определяют, может ли возникающее инфекционное заболевание распространиться среди населения, и определяют, какая часть населения должна быть иммунизирована путем вакцинации, чтобы искоренить болезнь. В широко используемых моделях инфекции , когда $R_{0}>1$ инфекция сможет начать распространяться среди населения, но не в том случае, если $R_{0}<1$ . Как правило, чем больше значение $R_{0}$ , тем труднее контролировать эпидемию. Для простых моделей доля населения, которую необходимо эффективно иммунизировать (то есть не восприимчивой к инфекции) для предотвращения устойчивого распространения инфекции, должна быть больше, чем $1-1/R_{0}$ . ^{[ 8 ]} Это так называемый коллективного иммунитета порог или уровень коллективного иммунитета . В данном случае коллективный иммунитет означает, что болезнь не может распространяться среди населения, поскольку каждый инфицированный человек в среднем может передать инфекцию менее чем одному другому контакту. ^{[ 9 ]} И наоборот, доля населения, которая остается восприимчивой к инфекции в условиях эндемического равновесия, равна $1/R_{0}$ . Однако этот порог основан на простых моделях, которые предполагают полностью смешанную популяцию без структурированных отношений между людьми. Например, если существует некоторая корреляция между статусом иммунизации (например, вакцинации) людей, то формула $1-1/R_{0}$ могут недооценивать порог коллективного иммунитета. ^{[ 9 ]}

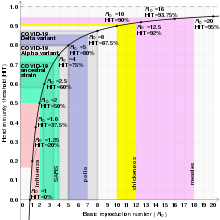
На базовую репродуктивную численность влияют несколько факторов, в том числе продолжительность инфекционности пораженных людей, контагиозность микроорганизма и количество восприимчивых людей в популяции, с которой контактируют инфицированные люди. ^{[ 10 ]}

История

Корни базовой концепции воспроизводства можно проследить в работах Рональда Росса , Альфреда Лотки и других. ^{[ 11 ]} но его первое современное применение в эпидемиологии было сделано Джорджем Макдональдом в 1952 году. ^{[ 12 ]} который построил популяционные модели распространения малярии . В своей работе он назвал величину базовой нормой воспроизводства и обозначил ее через $Z_{0}$ .

Обзор $R_{0}$ методы оценки

Отсекальные модели

Компартментальные модели представляют собой общий метод моделирования, часто применяемый для математического моделирования инфекционных заболеваний . В этих моделях члены популяции распределяются по «отсекам» с метками – например, S, I или R (восприимчивый, инфекционный или выздоровевший). Эти модели можно использовать для оценки $R_{0}$ .

Эпидемические модели в сетях

Эпидемии можно моделировать как заболевания, распространяющиеся через сети контактов и передачи болезней между людьми. ^{[ 13 ]} Узлы в этих сетях представляют отдельных лиц, а связи (ребра) между узлами представляют собой контакт или передачу заболевания между ними. Если такая сеть является локально древовидной, то базовое воспроизведение можно записать через среднюю степень избытка передающей сети так, что:

$R_{0}={\frac {\langle k^{2}\rangle }{\langle k\rangle }}-1,$

где ${\langle k\rangle }$ - средняя степень (средняя степень) сети и ${\langle k^{2}\rangle }$ — второй момент сети передачи распределения степени .

Гетерогенные популяции

В неоднородных популяциях определение $R_{0}$ является более тонким. В определении необходимо учитывать тот факт, что типичный инфицированный человек не может быть обычным человеком. В качестве крайнего примера рассмотрим популяцию, в которой небольшая часть особей полностью смешивается друг с другом, а остальные особи изолированы. Заболевание может распространяться в полностью смешанной части, даже если случайно выбранный человек приведет к менее чем одному вторичному случаю. Это связано с тем, что типичный инфицированный человек находится в полностью смешанной части и, таким образом, способен успешно вызывать инфекции. В целом, если лица, инфицированные на ранних стадиях эпидемии, в среднем либо с большей, либо с меньшей вероятностью передают инфекцию, чем лица, инфицированные на поздних стадиях эпидемии, то расчет $R_{0}$ должны учитывать эту разницу. Подходящее определение для $R_{0}$ в данном случае это «ожидаемое количество вторичных случаев, возникших в полностью восприимчивой популяции от типичного инфицированного человека». ^{[ 14 ]}

Базовое репродуктивное число можно рассчитать как соотношение известных показателей с течением времени: если заразный человек контактирует $\beta$ других людей в единицу времени, если предполагается, что все эти люди заразились этой болезнью и если болезнь имеет средний заразный период ${\dfrac {1}{\gamma }}$ , то базовое число воспроизводства равно $R_{0}={\dfrac {\beta }{\gamma }}$ . Некоторые заболевания имеют несколько возможных латентных периодов, и в этом случае число репродукций для заболевания в целом представляет собой сумму числа репродукций для каждого времени перехода к заболеванию.

Эффективное число воспроизводства

Объяснение

R

простыми словами от правительства Уэльса .

В действительности, различные доли населения в любой момент времени имеют иммунитет к той или иной болезни. Чтобы учесть это, эффективное число воспроизводства $R_{e}$ или $R$ используется. $R_{t}$ — среднее количество новых инфекций, вызванных одним инфицированным человеком в момент времени t среди частично восприимчивой популяции. Его можно найти, умножив $R_{0}$ долей S населения, которая восприимчива. Когда доля населения, обладающего иммунитетом, увеличивается (т. е. восприимчивая популяция S уменьшается) настолько, что $R_{e}$ опустится ниже, коллективный иммунитет и количество случаев заболевания среди населения постепенно снизится до нуля. достигнут ^{[ 15 ]}^{[ 16 ]}^{[ 17 ]}

Ограничения $R_{0}$

Использование $R_{0}$ в популярной прессе привело к неправильному пониманию и искажению его смысла. $R_{0}$ может быть рассчитана на основе множества различных математических моделей . Каждый из них может дать разную оценку $R_{0}$ , который необходимо интерпретировать в контексте этой модели. ^{[ 10 ]} Поэтому контагиозность разных инфекционных агентов нельзя сравнивать без пересчета. $R_{0}$ с инвариантными предположениями. $R_{0}$ значения для прошлых вспышек могут быть недействительны для текущих вспышек того же заболевания. Вообще говоря, $R_{0}$ может использоваться в качестве порога, даже если рассчитывается разными методами: если $R_{0}<1$ , вспышка затухнет, и если $R_{0}>1$ , вспышка будет расширяться. В некоторых случаях для некоторых моделей значения $R_{0}<1$ все еще может привести к самовоспроизводящимся вспышкам. Это особенно проблематично, если между хозяевами существуют промежуточные переносчики (как в случае зоонозов ), например малярия . ^{[ 18 ]} Поэтому сравнения значений из «Значений $R_{0}$ Таблицу известных инфекционных болезней» следует проводить с осторожностью.

Хотя $R_{0}$ не может быть изменено посредством вакцинации или других изменений в восприимчивости населения, оно может варьироваться в зависимости от ряда биологических, социально-поведенческих и экологических факторов. ^{[ 7 ]} Его также можно изменить с помощью физического дистанцирования и других мер государственной политики или социальных мер. ^{[ 19 ]}^{[ 7 ]} хотя некоторые исторические определения исключают любое преднамеренное вмешательство в снижение передачи заболеваний, включая нефармакологические вмешательства. ^{[ 3 ]} И действительно, включены ли нефармакологические вмешательства в $R_{0}$ часто зависит от статьи, заболевания и того, изучается ли какое-либо вмешательство. ^{[ 7 ]} Это создает некоторую путаницу, поскольку $R_{0}$ не является константой; тогда как большинство математических параметров с индексами «ноль» являются константами.

$R$ зависит от многих факторов, многие из которых необходимо оценить. Каждый из этих факторов увеличивает неопределенность в оценках $R$ . Многие из этих факторов не важны для информирования государственной политики. Таким образом, государственную политику могут лучше обслуживать показатели, подобные $R$ , но которые легче оценить, например время удвоения или период полураспада ( $t_{1/2}$ ). ^{[ 20 ]}^{[ 21 ]}

Методы, используемые для расчета $R_{0}$ включить функцию выживания , переставить наибольшее собственное значение матрицы Якоби , метод следующего поколения , ^{[ 22 ]} расчеты на основе собственного темпа роста, ^{[ 23 ]} наличие эндемического равновесия, число восприимчивых к эндемическому равновесию, средний возраст заражения ^{[ 24 ]} и окончательное уравнение размера. ^{[ 25 ]} Лишь немногие из этих методов согласуются друг с другом, даже если они начинаются с одной и той же системы дифференциальных уравнений . ^{[ 18 ]} Еще меньше людей реально подсчитывают среднее число вторичных инфекций. С $R_{0}$ редко наблюдается в полевых условиях и обычно рассчитывается с помощью математической модели, что серьезно ограничивает его полезность. ^{[ 26 ]}

Примерные значения для различных инфекционных заболеваний

Несмотря на трудности с оценкой $R_{0}$ Как упоминалось в предыдущем разделе, оценки были сделаны для ряда родов и показаны в этой таблице. Каждый род может состоять из многих видов , штаммов или вариантов . Оценки $R_{0}$ данные по видам, штаммам и вариантам обычно менее точны, чем по родам, поэтому они представлены в отдельных таблицах ниже для заболеваний, представляющих особый интерес ( грипп и COVID-19 ).

Значения R ₀ и пороги коллективного иммунитета (HIT) инфекционных заболеваний до вмешательства
Болезнь	Передача инфекции	R_Р0	УДАРЯТЬ ^{[ а ]}
Корь	Аэрозоль	12–18 ^{[ 27 ]}^{[ 7 ]}	92–94%
Ветряная оспа (ветряная оспа)	Аэрозоль	10–12 ^{[ 28 ]}	90–92%
Свинка	Респираторные капли	10–12 ^{[ 29 ]}	90–92%
COVID-19 (см. значения для конкретных штаммов ниже)	Респираторные капли и аэрозоли	2.9-9.5 ^{[ 30 ]}	65–89%
краснуха	Респираторные капли	6–7 ^{[ б ]}	83–86%
Полиомиелит	Фекально-оральный путь	5–7 ^{[ б ]}	80–86%
Коклюш	Респираторные капли	5.5 ^{[ 35 ]}	82%
оспа	Респираторные капли	3.5–6.0 ^{[ 36 ]}	71–83%
ВИЧ/СПИД	Жидкости организма	2–5 ^{[ 37 ]}	50–80%
ОРВИ	Респираторные капли	2–4 ^{[ 38 ]}	50–75%
Дифтерия	Слюна	2.6 ( 1.7 – 4.3 ) ^{[ 39 ]}	62% ( 41 – 77% )
Простуда (например, риновирус)	Респираторные капли	2–3 ^{[ 40 ]}^{[ нужна медицинская ссылка ]}	50–67%
Мпокс	Физический контакт, биологические жидкости, капли из дыхательных путей, половой контакт (МСМ)	2.1 ( 1.1 – 2.7 ) ^{[ 41 ]}^{[ 42 ]}	53% ( 22 – 63% )
Эбола ( вспышка 2014 г. )	Жидкости организма	1.8 ( 1.4 – 1.8 ) ^{[ 43 ]}	44% ( 31 – 44% )
Грипп (сезонные штаммы)	Респираторные капли	1.3 ( 1.2 – 1.4 ) ^{[ 44 ]}	23% ( 17 – 29% )
Андский хантавирус	Дыхательные капли и жидкости организма	1.2 ( 0.8 – 1.6 ) ^{[ 45 ]}	16% ( 0 – 36% ) ^{[ с ]}
Вирус Нипах	Жидкости организма	0.5 ^{[ 46 ]}	0% ^{[ с ]}
ПРОГУЛКА	Респираторные капли	0.5 ( 0.3 – 0.8 ) ^{[ 47 ]}	0% ^{[ с ]}

Оценки штаммов гриппа .

Значения R ₀ и пороги коллективного иммунитета (HIT) для конкретных штаммов гриппа
Болезнь	Передача инфекции	R_Р0	УДАРЯТЬ ^{[ а ]}
Грипп ( пандемический штамм 1918 года )	Респираторные капли	2 ^{[ 48 ]}	50%
Грипп ( пандемический штамм 2009 г. )	Респираторные капли	1.6 ( 1.3 – 2.0 ) ^{[ 2 ]}	37% ( 25 – 51% )
Грипп (сезонные штаммы)	Респираторные капли	1.3 ( 1.2 – 1.4 ) ^{[ 44 ]}	23% ( 17 – 29% )

Оценки вариантов SARS-CoV-2 .

Значения R ₀ и пороги коллективного иммунитета (HIT) для вариантов SARS-CoV-2
Болезнь	Передача инфекции	R_Р0	УДАРЯТЬ ^{[ а ]}
COVID-19 ( вариант Омикрона )	Респираторные капли и аэрозоли	9.5 ^{[ 30 ]}	89%
COVID-19 ( вариант Дельта )	Респираторные капли и аэрозоли	5.1 ^{[ 49 ]}	80%
COVID-19 ( альфа-вариант )	Респираторные капли и аэрозоли	4–5 ^{[ 50 ]}^{[ нужна медицинская ссылка ]}	75–80%
COVID-19 ( предковый штамм )	Респираторные капли и аэрозоли ^{[ 51 ]}	2.9 ( 2.4 – 3.4 ) ^{[ 52 ]}	65% ( 58 – 71% )

В популярной культуре

В фильме 2011 года «Заражение» , вымышленном медицинском триллере-катастрофе, расчеты блоггера $R_{0}$ представлены для отражения прогрессирования смертельной вирусной инфекции от единичных случаев до пандемии. ^{[ 19 ]}

См. также

Примечания

^ Перейти обратно: ^а ^б ^с Рассчитано с использованием $p = 1 − .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 1 / R 0 ⁠$ .
^ Перейти обратно: ^а ^б Из модуля обучающего курса ^{[ 31 ]} с измененными данными из других источников. ^{[ 32 ]}^{[ 33 ]}^{[ 34 ]}
^ Перейти обратно: ^а ^б ^с При R ₀ < 1,0 заболевание естественным образом исчезает.

Ссылки

^ Миллиган Г.Н., Барретт А.Д. (2015). Вакцинология: важное руководство . Чичестер, Западный Суссекс: Уайли Блэквелл. п. 310. ИСБН 978-1-118-63652-7 . OCLC 881386962 .
^ Перейти обратно: ^а ^б Фрейзер С., Доннелли К.А., Кошемес С., Ханаге В.П., Ван Керхове, доктор медицинских наук, Холлингсворт Т.Д. и др. (июнь 2009 г.). «Пандемический потенциал штамма гриппа А (H1N1): первые результаты» . Наука . 324 (5934): 1557–61. Бибкод : 2009Sci...324.1557F . дои : 10.1126/science.1176062 . ПМЦ 3735127 . ПМИД 19433588 .
^ Перейти обратно: ^а ^б Беккер Н.Г., Гласс К., Барнс Б., Кейли П., Филп Д., Маккоу Дж.М. и др. (апрель 2006 г.). «Номер репродукции» . Использование математических моделей для оценки мер реагирования на вспышку нового вирусного респираторного заболевания . Национальный центр эпидемиологии и здоровья населения. ISBN 1-74186-357-0 . Архивировано из оригинала 1 февраля 2020 года . Проверено 1 февраля 2020 г.
^ Адам Д. (июль 2020 г.). «Руководство по R – неправильно понятому показателю пандемии» . Природа . 583 (7816): 346–348. Бибкод : 2020Natur.583..346A . doi : 10.1038/d41586-020-02009-w . ПМИД 32620883 .
^ Джонс Дж. «Заметки о R0» (PDF) . Стэнфордский университет .
^ Сигел Э. «Почему «экспоненциальный рост» так страшен для коронавируса COVID-19» . Форбс . Проверено 19 марта 2020 г.
^ Перейти обратно: ^а ^б ^с ^д ^и Деламатер П.Л., Стрит Э.Дж., Лесли Т.Ф., Ян Ю.Т., Якобсен К.Х. (январь 2019 г.). «Сложность основного числа воспроизводства (R ₀ )» . Новые инфекционные заболевания . 25 (1): 1–4. дои : 10.3201/eid2501.171901 . ПМК 6302597 . ПМИД 30560777 .
^ Хорошо, П.; Имс, К.; Хейманн, Д.Л. (1 апреля 2011 г.). « «Стадный иммунитет»: грубое руководство» . Клинические инфекционные болезни . 52 (7): 911–916. дои : 10.1093/cid/cir007 . ПМИД 21427399 .
^ Перейти обратно: ^а ^б Хираока, Такаюки; К. Ризи, Аббас; Кивеля, Микко; Сарамяки, Яри (12 мая 2022 г.). «Коллективный иммунитет и размер эпидемии в сетях с прививочной гомофилией» . Физический обзор E . 105 (5): L052301. arXiv : 2112.07538 . Бибкод : 2022PhRvE.105e2301H . дои : 10.1103/PhysRevE.105.L052301 . ПМИД 35706197 . S2CID 245130970 .
^ Перейти обратно: ^а ^б Вегвари К. «Комментарий к использованию репродуктивного числа R во время пандемии COVID-19». Статические методы Med Res . ПМИД 34569883 .
^ Смит Д.Л., Баттл К.Е., Хэй С.И., Баркер С.М., Скотт Т.В., Маккензи Ф.Е. (5 апреля 2012 г.). «Росс, Макдональд и теория динамики и контроля патогенов, передающихся комарами» . ПЛОС Патогены . 8 (4): e1002588. doi : 10.1371/journal.ppat.1002588 . ПМК 3320609 . ПМИД 22496640 .
^ Макдональд Дж. (сентябрь 1952 г.). «Анализ равновесия при малярии». Бюллетень тропических болезней . 49 (9): 813–29. ПМИД 12995455 .
^ Сетевая наука Альберта-Ласло Барабаши .
^ Дикманн О, Хестербек Дж.А., Мец Дж.А. (1990). «Об определении и расчете базового коэффициента воспроизводства R0 в моделях инфекционных заболеваний в гетерогенных популяциях». Журнал математической биологии . 28 (4): 365–82. дои : 10.1007/BF00178324 . hdl : 1874/8051 . ПМИД 2117040 . S2CID 22275430 .
^ Гарнетт GP (февраль 2005 г.). «Роль коллективного иммунитета в определении эффекта вакцин против болезней, передающихся половым путем» . Журнал инфекционных болезней . 191 (Приложение 1): С97-106. дои : 10.1086/425271 . ПМИД 15627236 .
^ Родпотхонг П., Ауеваракул П. (октябрь 2012 г.). «Эволюция вируса и эффективность передачи» . Всемирный журнал вирусологии . 1 (5): 131–4. дои : 10.5501/wjv.v1.i5.131 . ПМЦ 3782273 . ПМИД 24175217 .
^ Даббагян В., Маго В.К. (2013). Теории и моделирование сложных социальных систем . Спрингер. стр. 134–35. ISBN 978-3642391491 . Проверено 29 марта 2015 г.
^ Перейти обратно: ^а ^б Ли Дж., Блейкли Д., Смит Р.Дж. (2011). «Отказ R0» . Вычислительные и математические методы в медицине . 2011 (527610): 527610. doi : 10.1155/2011/527610 . ПМК 3157160 . ПМИД 21860658 .
^ Перейти обратно: ^а ^б Бирн М. (6 октября 2014 г.), «Неправильно понятое число, которое предсказывает эпидемии» , vice.com , получено 23 марта 2020 г.
^ Балкев Т.М. (декабрь 2010 г.). Модель SIR, когда S(t) является мультиэкспоненциальной функцией (тезис). Государственный университет Восточного Теннесси.
^ Ирландия MW, изд. (1928). Медицинский департамент армии США в мировой войне, том. IX: Инфекционные и другие болезни . Вашингтон: США: Типография правительства США. стр. 116–7.
^ Дикманн О, Хестербек Дж.А. (2000). «Базовый коэффициент воспроизводства» . Математическая эпидемиология инфекционных болезней: построение моделей, анализ и интерпретация . Нью-Йорк: Уайли. стр. 73–98. ISBN 0-471-49241-8 .
^ Чоуэлл Дж., Хенгартнер Н.В., Кастильо-Чавес К., Фенимор П.В., Хайман Дж.М. (июль 2004 г.). «Основное репродуктивное число Эболы и последствия мер общественного здравоохранения: случаи Конго и Уганды». Журнал теоретической биологии . 229 (1): 119–26. arXiv : q-bio/0503006 . Бибкод : 2004JThBi.229..119C . дои : 10.1016/j.jtbi.2004.03.006 . ПМИД 15178190 . S2CID 7298792 .
^ Аджелли М., Яннелли М., Манфреди П., Чиофи дельи Атти М.Л. (март 2008 г.). «Базовые математические модели временной динамики ВГА в среднеэндемичных регионах Италии». Вакцина . 26 (13): 1697–707. doi : 10.1016/j.vaccine.2007.12.058 . ПМИД 18314231 .
^ фон Чефалвай, Крис (1 января 2023 г.), фон Чефалвай, Крис (редактор), «2 - Простые разделенные модели: основа математической эпидемиологии» , Вычислительное моделирование инфекционных заболеваний , Academic Press, стр. 19–91, doi : 10.1016/b978-0-32-395389-4.00011-6 , ISBN 978-0-323-95389-4 , получено 2 марта 2023 г.
^ Хеффернан Дж. М., Смит Р. Дж., Валь Л. М. (сентябрь 2005 г.). «Перспективы базового репродуктивного коэффициента» . Журнал Королевского общества, Интерфейс . 2 (4): 281–93. дои : 10.1098/rsif.2005.0042 . ПМЦ 1578275 . ПМИД 16849186 .
^ Герра Ф.М., Болотин С., Лим Дж., Хеффернан Дж., Дикс С.Л., Ли Ю., Кроукрофт Н.С. (декабрь 2017 г.). «Основное репродуктивное число (R ₀ ) кори: систематический обзор». «Ланцет». Инфекционные болезни . 17 (12): е420–е428. дои : 10.1016/S1473-3099(17)30307-9 . ПМИД 28757186 .
^ Службы здравоохранения Ирландии. Информация для медицинских работников (PDF) . Проверено 27 марта 2020 г.
^ Министерства здравоохранения Австралии Определение лабораторного случая эпидемического паротита (LCD)
^ Перейти обратно: ^а ^б Лю, Ю (9 марта 2022 г.). «Эффективное репродуктивное число варианта Омикрон SARS-CoV-2 в несколько раз превышает число Дельта» . Журнал туристической медицины . 29 (3). Таблица 1. doi : 10.1093/jtm/taac037 . ISSN 1708-8305 . ПМЦ 8992231 . ПМИД 35262737 .
^ Центры по контролю и профилактике заболеваний; Всемирная организация здравоохранения (2001). «История и эпидемиология глобальной ликвидации оспы». Оспа: заболевание, профилактика и вмешательство (учебный курс) (Презентация). Атланта: Центры по контролю и профилактике заболеваний (опубликовано 25 августа 2014 г.). компакт-диск: 27929. Архивировано (PDF) из оригинала 17 марта 2017 г. Проверено 17 июня 2021 г.
^ Хорошо, Пол Э.М. (1993). «Коллективный иммунитет: история, теория, практика». Эпидемиологические обзоры . 15 (2): 265–302. doi : 10.1093/oxfordjournals.epirev.a036121 . ПМИД 8174658 .
^ Луман, ET; Баркер, Ле; Симпсон, DM; Родевальд, Луизиана; Силадьи, П.Г.; Чжао, Z (май 2001 г.). «Уровни охвата вакцинацией детей в возрасте 19–35 месяцев на национальном уровне, в штате и в городах, США, 1999». Американский журнал профилактической медицины . 20 (4): 88–153. дои : 10.1016/s0749-3797(01)00274-4 . ПМИД 12174806 .
^ Джайлс, РБ; Фукс, С; Клевенс, Р.М. (22 сентября 2000 г.). «Охват вакцинацией детей, обучающихся в программах Head Start, детских садах или поступающих в школу» . Еженедельный отчет о заболеваемости и смертности . 49 (9): 27–38. ПМИД 11016876 .
^ Кречмар М., Теунис П.Ф., Пебоди Р.Г. (июнь 2010 г.). «Заболеваемость и показатели воспроизводства коклюша: оценки на основе серологических данных и данных социальных контактов в пяти европейских странах» . ПЛОС Медицина . 7 (6): e1000291. дои : 10.1371/journal.pmed.1000291 . ПМЦ 2889930 . ПМИД 20585374 .
^ Гани Р., Лич С. (декабрь 2001 г.). «Потенциал передачи оспы среди современного населения» . Природа . 414 (6865): 748–51. Бибкод : 2001Natur.414..748G . дои : 10.1038/414748a . ПМИД 11742399 . S2CID 52799168 . Проверено 18 марта 2020 г.
^ «Игра в цифры: R0» . Национальный учебно-образовательный центр по новым специальным патогенам. 30 января 2020 года. Архивировано из оригинала 12 мая 2020 года . Проверено 27 декабря 2020 г. [...] в то время как инфекции, требующие полового контакта, такие как ВИЧ, имеют более низкий R ₀ (2-5).
^ Согласительный документ по эпидемиологии тяжелого острого респираторного синдрома (ТОРС) . Департамент эпиднадзора за инфекционными заболеваниями и реагирования на них (Технический отчет). Всемирная организация здравоохранения . п. 26. HDL : 10665/70863 . ВОЗ/CDS/CSR/GAR/2003.11. Ряд исследователей оценили базовую воспроизводственную численность, подобрав модели к начальному росту эпидемий в ряде стран. Их наблюдения показывают, что SARS-CoV менее заразен, чем первоначально предполагалось, с оценками Ro в диапазоне 2-4.
^ Трулав С.А., Киган Л.Т., Мосс В.Дж., Чессон Л.Х., Мейчер Э., Азман А.С., Лесслер Дж. (июнь 2020 г.). «Клинические и эпидемиологические аспекты дифтерии: систематический обзор и объединенный анализ» . Клинические инфекционные болезни . 71 (1): 89–97. дои : 10.1093/cid/ciz808 . ПМЦ 7312233 . ПМИД 31425581 .
^ Фриман С. (6 ноября 2014 г.). «Волшебная формула, которая определит, побеждена ли Эбола» . Телеграф . Телеграф.Ко.Великобритания. Архивировано из оригинала 12 января 2022 года . Проверено 30 марта 2020 г.
^ Грант Р., Нгуен Л.Л., Бребан Р. (1 сентября 2020 г.). «Моделирование передачи оспы обезьян от человека к человеку» (PDF) . Бюллетень Всемирной организации здравоохранения . 98 (9): 638–640. дои : 10.2471/BLT.19.242347 . ISSN 0042-9686 . ПМЦ 7463189 . ПМИД 33012864 . Архивировано из оригинала (PDF) 11 декабря 2020 г.
^ Аль-Раи М. (февраль 2023 г.). «Изучение заболевания оспой человека в 2022 году с использованием эпидемических моделей: коллективный иммунитет и базовое репродуктивное число случаев» . Анналы медицины и хирургии . 85 (2): 316–321. дои : 10.1097/MS9.0000000000000229 . ISSN 2049-0801 . ПМЦ 9949786 . ПМИД 36845803 .
^ Вонг З.С., Буй С.М., Чухтай А.А., Макинтайр Ч.Р. (апрель 2017 г.). «Систематический обзор ранних исследований по моделированию болезни, вызванной вирусом Эбола, в Западной Африке» . Эпидемиология и инфекции . 145 (6): 1069–1094. дои : 10.1017/S0950268817000164 . ПМЦ 9507849 . ПМИД 28166851 . Медиана средней оценки R ₀ для продолжающейся эпидемии (в целом) составляет 1,78 (межквартильный размах: 1,44, 1,80).
^ Перейти обратно: ^а ^б Чоуэлл Дж., Миллер М.А., Вибуд С. (июнь 2008 г.). «Сезонный грипп в США, Франции и Австралии: передача и перспективы борьбы» . Эпидемиология и инфекции . 136 (6). Издательство Кембриджского университета : 852–64. дои : 10.1017/S0950268807009144 . ПМК 2680121 . ПМИД 17634159 . Коэффициент воспроизводства в разные сезоны гриппа и в разных странах находился в диапазоне 0,9–2,0 при общем среднем значении 1,3 и 95% доверительном интервале (ДИ) 1,2–1,4.
^ Мартинес, Валерия П.; ДиПаола, Николас; Алонсо, Дэниел О.; Перес-Сауту, Унаи; Белломо, Карла М.; Иглесиас, Айелен А.; и др. (3 декабря 2020 г.). « Суперраспространители» и передача Андского вируса от человека к человеку в Аргентине» . Медицинский журнал Новой Англии . 383 (23): 2230–2241. дои : 10.1056/NEJMoa2009040 . PMID 33264545 . S2CID 227259435 .
^ Лубы СП (октябрь 2013 г.). «Пандемический потенциал вируса Нипах». Противовирусные исследования . 100 (1): 38–43. дои : 10.1016/j.antiviral.2013.07.011 . ПМИД 23911335 .
^ Кучарский А.Я., Althaus CL (июнь 2015 г.). «Роль сверхраспространения в передаче коронавируса ближневосточного респираторного синдрома (MERS-CoV)» . Евронаблюдение . 20 (25): 14–8. дои : 10.2807/1560-7917.ES2015.20.25.21167 . ПМИД 26132768 .
^ «Передача Омикрона: как распространяются заразные болезни» . Медицина Небраски . 21 декабря 2021 . Проверено 25 января 2022 г.
^ Лю, Ин; Роклов, Иоаким (1 октября 2021 г.). «Репродуктивная численность дельта-варианта SARS-CoV-2 намного выше по сравнению с предковым вирусом SARS-CoV-2» . Журнал туристической медицины . 28 (7). дои : 10.1093/jtm/taab124 . ISSN 1708-8305 . ПМЦ 8436367 . ПМИД 34369565 .
^ Галлахер, Джеймс (12 июня 2021 г.). «Covid: есть ли предел тому, насколько худшие варианты могут стать?» . Новости Би-би-си . Проверено 21 июля 2021 г.
^ Пратер, Кимберли А.; Марр, Линси С.; Шули, Роберт Т.; МакДиармид, Мелисса А.; Уилсон, Мэри Э.; Милтон, Дональд К. (16 октября 2020 г.). «Воздушно-капельная передача SARS-CoV-2». Наука . 370 (6514): 303,2–304. Бибкод : 2020Sci...370..303P . дои : 10.1126/science.abf0521 . ПМИД 33020250 . S2CID 222145689 .
^ Биллах, Ариф; Миа, Мамун; Хан, Нуруззаман (11 ноября 2020 г.). «Репродуктивное число коронавируса: систематический обзор и метаанализ, основанный на доказательствах глобального уровня» . ПЛОС ОДИН . 15 (11): e0242128. Бибкод : 2020PLoSO..1542128B . дои : 10.1371/journal.pone.0242128 . ПМЦ 7657547 . ПМИД 33175914 .

Дальнейшее чтение

У Scholia есть профиль для основного номера воспроизводства (Q901464) .

Хестербек, Япония (2002). «Краткая история R0 и рецепт его расчета». Acta Biotheoretica . 50 (3): 189–204. дои : 10.1023/а:1016599411804 . hdl : 1874/383700 . ПМИД 12211331 . S2CID 10178944 .
Хеффернан, Дж. М.; Смит, Р.Дж.; Валь, Л.М. (22 сентября 2005 г.). «Перспективы базового репродуктивного коэффициента» . Журнал интерфейса Королевского общества . 2 (4): 281–293. дои : 10.1098/rsif.2005.0042 . ПМЦ 1578275 . ПМИД 16849186 .
Джонс Дж. Х. (1 мая 2007 г.). «Заметки о $R_{0}$ . (PDF) Проверено 6 ноября 2018 года .
Ван Ден Дриссе, П.; Уотмо, Джеймс (2008). «Дальнейшие примечания к базовому репродукционному номеру». Математическая эпидемиология . Конспект лекций по математике. Том. 1945. стр. 159–178. дои : 10.1007/978-3-540-78911-6_6 . ISBN 978-3-540-78910-9 .

[calc-27] Перейти обратно: ^а ^б ^с Рассчитано с использованием $p = 1 − .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 1 / R 0 ⁠$ .

[cdc-who-2001-36] Перейти обратно: ^а ^б Из модуля обучающего курса ^{[ 31 ]} с измененными данными из других источников. ^{[ 32 ]}^{[ 33 ]}^{[ 34 ]}

[lowr-48] Перейти обратно: ^а ^б ^с При R ₀ < 1,0 заболевание естественным образом исчезает.

[1] Миллиган Г.Н., Барретт А.Д. (2015). Вакцинология: важное руководство . Чичестер, Западный Суссекс: Уайли Блэквелл. п. 310. ИСБН 978-1-118-63652-7 . OCLC 881386962 .

[Fraser-2] Перейти обратно: ^а ^б Фрейзер С., Доннелли К.А., Кошемес С., Ханаге В.П., Ван Керхове, доктор медицинских наук, Холлингсворт Т.Д. и др. (июнь 2009 г.). «Пандемический потенциал штамма гриппа А (H1N1): первые результаты» . Наука . 324 (5934): 1557–61. Бибкод : 2009Sci...324.1557F . дои : 10.1126/science.1176062 . ПМЦ 3735127 . ПМИД 19433588 .

[:0-3] Перейти обратно: ^а ^б Беккер Н.Г., Гласс К., Барнс Б., Кейли П., Филп Д., Маккоу Дж.М. и др. (апрель 2006 г.). «Номер репродукции» . Использование математических моделей для оценки мер реагирования на вспышку нового вирусного респираторного заболевания . Национальный центр эпидемиологии и здоровья населения. ISBN 1-74186-357-0 . Архивировано из оригинала 1 февраля 2020 года . Проверено 1 февраля 2020 г.

[4] Адам Д. (июль 2020 г.). «Руководство по R – неправильно понятому показателю пандемии» . Природа . 583 (7816): 346–348. Бибкод : 2020Natur.583..346A . doi : 10.1038/d41586-020-02009-w . ПМИД 32620883 .

[5] Джонс Дж. «Заметки о R0» (PDF) . Стэнфордский университет .

[6] Сигел Э. «Почему «экспоненциальный рост» так страшен для коронавируса COVID-19» . Форбс . Проверено 19 марта 2020 г.

[Delamater-7] Перейти обратно: ^а ^б ^с ^д ^и Деламатер П.Л., Стрит Э.Дж., Лесли Т.Ф., Ян Ю.Т., Якобсен К.Х. (январь 2019 г.). «Сложность основного числа воспроизводства (R ₀ )» . Новые инфекционные заболевания . 25 (1): 1–4. дои : 10.3201/eid2501.171901 . ПМК 6302597 . ПМИД 30560777 .

[8] Хорошо, П.; Имс, К.; Хейманн, Д.Л. (1 апреля 2011 г.). « «Стадный иммунитет»: грубое руководство» . Клинические инфекционные болезни . 52 (7): 911–916. дои : 10.1093/cid/cir007 . ПМИД 21427399 .

[:1-9] Перейти обратно: ^а ^б Хираока, Такаюки; К. Ризи, Аббас; Кивеля, Микко; Сарамяки, Яри (12 мая 2022 г.). «Коллективный иммунитет и размер эпидемии в сетях с прививочной гомофилией» . Физический обзор E . 105 (5): L052301. arXiv : 2112.07538 . Бибкод : 2022PhRvE.105e2301H . дои : 10.1103/PhysRevE.105.L052301 . ПМИД 35706197 . S2CID 245130970 .

[Vegvari-10] Перейти обратно: ^а ^б Вегвари К. «Комментарий к использованию репродуктивного числа R во время пандемии COVID-19». Статические методы Med Res . ПМИД 34569883 .

[11] Смит Д.Л., Баттл К.Е., Хэй С.И., Баркер С.М., Скотт Т.В., Маккензи Ф.Е. (5 апреля 2012 г.). «Росс, Макдональд и теория динамики и контроля патогенов, передающихся комарами» . ПЛОС Патогены . 8 (4): e1002588. doi : 10.1371/journal.ppat.1002588 . ПМК 3320609 . ПМИД 22496640 .

[12] Макдональд Дж. (сентябрь 1952 г.). «Анализ равновесия при малярии». Бюллетень тропических болезней . 49 (9): 813–29. ПМИД 12995455 .

[13] Сетевая наука Альберта-Ласло Барабаши .

[Diekmann-14] Дикманн О, Хестербек Дж.А., Мец Дж.А. (1990). «Об определении и расчете базового коэффициента воспроизводства R0 в моделях инфекционных заболеваний в гетерогенных популяциях». Журнал математической биологии . 28 (4): 365–82. дои : 10.1007/BF00178324 . hdl : 1874/8051 . ПМИД 2117040 . S2CID 22275430 .

[pmid15627236-15] Гарнетт GP (февраль 2005 г.). «Роль коллективного иммунитета в определении эффекта вакцин против болезней, передающихся половым путем» . Журнал инфекционных болезней . 191 (Приложение 1): С97-106. дои : 10.1086/425271 . ПМИД 15627236 .

[pmid24175217-16] Родпотхонг П., Ауеваракул П. (октябрь 2012 г.). «Эволюция вируса и эффективность передачи» . Всемирный журнал вирусологии . 1 (5): 131–4. дои : 10.5501/wjv.v1.i5.131 . ПМЦ 3782273 . ПМИД 24175217 .

[dabmago-17] Даббагян В., Маго В.К. (2013). Теории и моделирование сложных социальных систем . Спрингер. стр. 134–35. ISBN 978-3642391491 . Проверено 29 марта 2015 г.

[Li_&_Blakely-18] Перейти обратно: ^а ^б Ли Дж., Блейкли Д., Смит Р.Дж. (2011). «Отказ R0» . Вычислительные и математические методы в медицине . 2011 (527610): 527610. doi : 10.1155/2011/527610 . ПМК 3157160 . ПМИД 21860658 .

[Byrne-19] Перейти обратно: ^а ^б Бирн М. (6 октября 2014 г.), «Неправильно понятое число, которое предсказывает эпидемии» , vice.com , получено 23 марта 2020 г.

[Balkew-20] Балкев Т.М. (декабрь 2010 г.). Модель SIR, когда S(t) является мультиэкспоненциальной функцией (тезис). Государственный университет Восточного Теннесси.

[Ireland-21] Ирландия MW, изд. (1928). Медицинский департамент армии США в мировой войне, том. IX: Инфекционные и другие болезни . Вашингтон: США: Типография правительства США. стр. 116–7.

[22] Дикманн О, Хестербек Дж.А. (2000). «Базовый коэффициент воспроизводства» . Математическая эпидемиология инфекционных болезней: построение моделей, анализ и интерпретация . Нью-Йорк: Уайли. стр. 73–98. ISBN 0-471-49241-8 .

[23] Чоуэлл Дж., Хенгартнер Н.В., Кастильо-Чавес К., Фенимор П.В., Хайман Дж.М. (июль 2004 г.). «Основное репродуктивное число Эболы и последствия мер общественного здравоохранения: случаи Конго и Уганды». Журнал теоретической биологии . 229 (1): 119–26. arXiv : q-bio/0503006 . Бибкод : 2004JThBi.229..119C . дои : 10.1016/j.jtbi.2004.03.006 . ПМИД 15178190 . S2CID 7298792 .

[24] Аджелли М., Яннелли М., Манфреди П., Чиофи дельи Атти М.Л. (март 2008 г.). «Базовые математические модели временной динамики ВГА в среднеэндемичных регионах Италии». Вакцина . 26 (13): 1697–707. doi : 10.1016/j.vaccine.2007.12.058 . ПМИД 18314231 .

[25] фон Чефалвай, Крис (1 января 2023 г.), фон Чефалвай, Крис (редактор), «2 - Простые разделенные модели: основа математической эпидемиологии» , Вычислительное моделирование инфекционных заболеваний , Academic Press, стр. 19–91, doi : 10.1016/b978-0-32-395389-4.00011-6 , ISBN 978-0-323-95389-4 , получено 2 марта 2023 г.

[26] Хеффернан Дж. М., Смит Р. Дж., Валь Л. М. (сентябрь 2005 г.). «Перспективы базового репродуктивного коэффициента» . Журнал Королевского общества, Интерфейс . 2 (4): 281–93. дои : 10.1098/rsif.2005.0042 . ПМЦ 1578275 . ПМИД 16849186 .

[28] Герра Ф.М., Болотин С., Лим Дж., Хеффернан Дж., Дикс С.Л., Ли Ю., Кроукрофт Н.С. (декабрь 2017 г.). «Основное репродуктивное число (R ₀ ) кори: систематический обзор». «Ланцет». Инфекционные болезни . 17 (12): е420–е428. дои : 10.1016/S1473-3099(17)30307-9 . ПМИД 28757186 .

[29] Службы здравоохранения Ирландии. Информация для медицинских работников (PDF) . Проверено 27 марта 2020 г.

[30] Министерства здравоохранения Австралии Определение лабораторного случая эпидемического паротита (LCD)

[jtm2022-31] Перейти обратно: ^а ^б Лю, Ю (9 марта 2022 г.). «Эффективное репродуктивное число варианта Омикрон SARS-CoV-2 в несколько раз превышает число Дельта» . Журнал туристической медицины . 29 (3). Таблица 1. doi : 10.1093/jtm/taac037 . ISSN 1708-8305 . ПМЦ 8992231 . ПМИД 35262737 .

[32] Центры по контролю и профилактике заболеваний; Всемирная организация здравоохранения (2001). «История и эпидемиология глобальной ликвидации оспы». Оспа: заболевание, профилактика и вмешательство (учебный курс) (Презентация). Атланта: Центры по контролю и профилактике заболеваний (опубликовано 25 августа 2014 г.). компакт-диск: 27929. Архивировано (PDF) из оригинала 17 марта 2017 г. Проверено 17 июня 2021 г.

[33] Хорошо, Пол Э.М. (1993). «Коллективный иммунитет: история, теория, практика». Эпидемиологические обзоры . 15 (2): 265–302. doi : 10.1093/oxfordjournals.epirev.a036121 . ПМИД 8174658 .

[34] Луман, ET; Баркер, Ле; Симпсон, DM; Родевальд, Луизиана; Силадьи, П.Г.; Чжао, Z (май 2001 г.). «Уровни охвата вакцинацией детей в возрасте 19–35 месяцев на национальном уровне, в штате и в городах, США, 1999». Американский журнал профилактической медицины . 20 (4): 88–153. дои : 10.1016/s0749-3797(01)00274-4 . ПМИД 12174806 .

[35] Джайлс, РБ; Фукс, С; Клевенс, Р.М. (22 сентября 2000 г.). «Охват вакцинацией детей, обучающихся в программах Head Start, детских садах или поступающих в школу» . Еженедельный отчет о заболеваемости и смертности . 49 (9): 27–38. ПМИД 11016876 .

[37] Кречмар М., Теунис П.Ф., Пебоди Р.Г. (июнь 2010 г.). «Заболеваемость и показатели воспроизводства коклюша: оценки на основе серологических данных и данных социальных контактов в пяти европейских странах» . ПЛОС Медицина . 7 (6): e1000291. дои : 10.1371/journal.pmed.1000291 . ПМЦ 2889930 . ПМИД 20585374 .

[38] Гани Р., Лич С. (декабрь 2001 г.). «Потенциал передачи оспы среди современного населения» . Природа . 414 (6865): 748–51. Бибкод : 2001Natur.414..748G . дои : 10.1038/414748a . ПМИД 11742399 . S2CID 52799168 . Проверено 18 марта 2020 г.

[39] «Игра в цифры: R0» . Национальный учебно-образовательный центр по новым специальным патогенам. 30 января 2020 года. Архивировано из оригинала 12 мая 2020 года . Проверено 27 декабря 2020 г. [...] в то время как инфекции, требующие полового контакта, такие как ВИЧ, имеют более низкий R ₀ (2-5).

[40] Согласительный документ по эпидемиологии тяжелого острого респираторного синдрома (ТОРС) . Департамент эпиднадзора за инфекционными заболеваниями и реагирования на них (Технический отчет). Всемирная организация здравоохранения . п. 26. HDL : 10665/70863 . ВОЗ/CDS/CSR/GAR/2003.11. Ряд исследователей оценили базовую воспроизводственную численность, подобрав модели к начальному росту эпидемий в ряде стран. Их наблюдения показывают, что SARS-CoV менее заразен, чем первоначально предполагалось, с оценками Ro в диапазоне 2-4.

[41] Трулав С.А., Киган Л.Т., Мосс В.Дж., Чессон Л.Х., Мейчер Э., Азман А.С., Лесслер Дж. (июнь 2020 г.). «Клинические и эпидемиологические аспекты дифтерии: систематический обзор и объединенный анализ» . Клинические инфекционные болезни . 71 (1): 89–97. дои : 10.1093/cid/ciz808 . ПМЦ 7312233 . ПМИД 31425581 .

[Telegraph_Ebola-42] Фриман С. (6 ноября 2014 г.). «Волшебная формула, которая определит, побеждена ли Эбола» . Телеграф . Телеграф.Ко.Великобритания. Архивировано из оригинала 12 января 2022 года . Проверено 30 марта 2020 г.

[43] Грант Р., Нгуен Л.Л., Бребан Р. (1 сентября 2020 г.). «Моделирование передачи оспы обезьян от человека к человеку» (PDF) . Бюллетень Всемирной организации здравоохранения . 98 (9): 638–640. дои : 10.2471/BLT.19.242347 . ISSN 0042-9686 . ПМЦ 7463189 . ПМИД 33012864 . Архивировано из оригинала (PDF) 11 декабря 2020 г.

[44] Аль-Раи М. (февраль 2023 г.). «Изучение заболевания оспой человека в 2022 году с использованием эпидемических моделей: коллективный иммунитет и базовое репродуктивное число случаев» . Анналы медицины и хирургии . 85 (2): 316–321. дои : 10.1097/MS9.0000000000000229 . ISSN 2049-0801 . ПМЦ 9949786 . ПМИД 36845803 .

[45] Вонг З.С., Буй С.М., Чухтай А.А., Макинтайр Ч.Р. (апрель 2017 г.). «Систематический обзор ранних исследований по моделированию болезни, вызванной вирусом Эбола, в Западной Африке» . Эпидемиология и инфекции . 145 (6): 1069–1094. дои : 10.1017/S0950268817000164 . ПМЦ 9507849 . ПМИД 28166851 . Медиана средней оценки R ₀ для продолжающейся эпидемии (в целом) составляет 1,78 (межквартильный размах: 1,44, 1,80).

[Cambridge_University_Press-46] Перейти обратно: ^а ^б Чоуэлл Дж., Миллер М.А., Вибуд С. (июнь 2008 г.). «Сезонный грипп в США, Франции и Австралии: передача и перспективы борьбы» . Эпидемиология и инфекции . 136 (6). Издательство Кембриджского университета : 852–64. дои : 10.1017/S0950268807009144 . ПМК 2680121 . ПМИД 17634159 . Коэффициент воспроизводства в разные сезоны гриппа и в разных странах находился в диапазоне 0,9–2,0 при общем среднем значении 1,3 и 95% доверительном интервале (ДИ) 1,2–1,4.

[47] Мартинес, Валерия П.; ДиПаола, Николас; Алонсо, Дэниел О.; Перес-Сауту, Унаи; Белломо, Карла М.; Иглесиас, Айелен А.; и др. (3 декабря 2020 г.). « Суперраспространители» и передача Андского вируса от человека к человеку в Аргентине» . Медицинский журнал Новой Англии . 383 (23): 2230–2241. дои : 10.1056/NEJMoa2009040 . PMID 33264545 . S2CID 227259435 .

[49] Лубы СП (октябрь 2013 г.). «Пандемический потенциал вируса Нипах». Противовирусные исследования . 100 (1): 38–43. дои : 10.1016/j.antiviral.2013.07.011 . ПМИД 23911335 .

[50] Кучарский А.Я., Althaus CL (июнь 2015 г.). «Роль сверхраспространения в передаче коронавируса ближневосточного респираторного синдрома (MERS-CoV)» . Евронаблюдение . 20 (25): 14–8. дои : 10.2807/1560-7917.ES2015.20.25.21167 . ПМИД 26132768 .

[51] «Передача Омикрона: как распространяются заразные болезни» . Медицина Небраски . 21 декабря 2021 . Проверено 25 января 2022 г.

[52] Лю, Ин; Роклов, Иоаким (1 октября 2021 г.). «Репродуктивная численность дельта-варианта SARS-CoV-2 намного выше по сравнению с предковым вирусом SARS-CoV-2» . Журнал туристической медицины . 28 (7). дои : 10.1093/jtm/taab124 . ISSN 1708-8305 . ПМЦ 8436367 . ПМИД 34369565 .

[bbc-sarscov2-variants-53] Галлахер, Джеймс (12 июня 2021 г.). «Covid: есть ли предел тому, насколько худшие варианты могут стать?» . Новости Би-би-си . Проверено 21 июля 2021 г.

[ScienceAirborne-54] Пратер, Кимберли А.; Марр, Линси С.; Шули, Роберт Т.; МакДиармид, Мелисса А.; Уилсон, Мэри Э.; Милтон, Дональд К. (16 октября 2020 г.). «Воздушно-капельная передача SARS-CoV-2». Наука . 370 (6514): 303,2–304. Бибкод : 2020Sci...370..303P . дои : 10.1126/science.abf0521 . ПМИД 33020250 . S2CID 222145689 .

[Reproductive_number_of_coronavirus-55] Биллах, Ариф; Миа, Мамун; Хан, Нуруззаман (11 ноября 2020 г.). «Репродуктивное число коронавируса: систематический обзор и метаанализ, основанный на доказательствах глобального уровня» . ПЛОС ОДИН . 15 (11): e0242128. Бибкод : 2020PLoSO..1542128B . дои : 10.1371/journal.pone.0242128 . ПМЦ 7657547 . ПМИД 33175914 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ а ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ б ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ с ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]