Термин (логика)
В математической логике термин формула обозначает математический объект, а обозначает математический факт. В частности, термины появляются как компоненты формулы. Это аналогично естественному языку, где именное словосочетание относится к объекту, а целое предложение относится к факту.
Терм первого порядка из рекурсивно конструируется константных символов, переменных и функциональных символов . Выражение, сформированное путем применения символа-предиката к соответствующему числу терминов, называется атомарной формулой значение дает истинное или ложное , которая в бивалентной логике при определенной интерпретации . Например, — это термин, построенный из константы 1, переменной x и символов двоичной функции и ; это часть атомной формулы который имеет значение true для каждого действительного значения x .
Помимо логики , термины играют важную роль в универсальной алгебре и системах переписывания .
Формальное определение
[ редактировать ]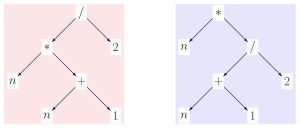
Учитывая набор V переменных символов, набор C постоянных символов и наборы F n из n -арных функциональных символов, также называемых операторными символами, для каждого натурального числа n ≥ 1 набор (несортированных) термов первого порядка T равен рекурсивно определяется как наименьший набор со следующими свойствами: [ 1 ]
- каждый переменный символ является термом: V ⊆ T ,
- каждый постоянный символ является термом: C ⊆ T ,
- из каждых n термов t 1 ,..., t n и каждого n -арного функционального символа f ∈ F n больший терм f ( t 1 , ..., t n ). можно построить
Используя интуитивно понятные псевдограмматические обозначения , это иногда записывается так:
- т ::= х | с е ( т 1 , ..., т н ).
Сигнатура F термина «язык» описывает, какие наборы функциональных символов n являются обитаемыми. Хорошо известными примерами являются символы унарной функции sin , cos ∈ F 1 и символы двоичной функции +, −, ⋅, / ∈ F 2 . Тернарные операции и функции более высокой арности возможны, но на практике встречаются редко. Многие авторы рассматривают константные символы как 0-арные функциональные символы F 0 , поэтому для них не требуется специального синтаксического класса.
Термин обозначает математический объект из области дискурса . Константа c обозначает именованный объект из этого домена, переменная x варьируется по объектам в этом домене, а n -арная функция f отображает n - кортежи объектов в объекты. Например, если n € V — переменный символ, 1 € C — постоянный символ, а add € F 2 — символ двоичной функции, то n € T , 1 € T и (следовательно) add ( n , 1) ∈ T по первому, второму и третьему правилам построения членов соответственно. Последний термин обычно записывается как n +1, используя для удобства инфиксную запись и более распространенный символ оператора +.
Временная структура против представления
[ редактировать ]Первоначально логики определяли термин как строку символов, соответствующую определенным правилам построения. [ 2 ] Однако, поскольку концепция дерева стала популярной в информатике, оказалось удобнее думать о таком термине как о дереве. Например, несколько отдельных строк символов, например " ( n ⋅( n +1))/2 ", " (( n ⋅( n +1)))/2 " и " «обозначают один и тот же термин и соответствуют одному и тому же дереву, а именно левому дереву на рисунке выше. Отделяя древовидную структуру термина от его графического представления на бумаге, также легко учесть круглые скобки (являющиеся лишь представлением, а не структурой) и невидимые операторы умножения (существующие только в структуре, а не в представлении).
Структурное равенство
[ редактировать ]Два термина считаются структурно , буквально или синтаксически равными, если они соответствуют одному и тому же дереву. Например, левое и правое дерево на рисунке выше являются структурно неравными терминами, хотя их можно считать « семантически равными », поскольку они всегда дают одно и то же значение в рациональной арифметике . Хотя структурное равенство можно проверить без каких-либо знаний о значении символов, семантическое равенство невозможно. Если функция /, например, интерпретируется не как рациональная, а как усекающее целочисленное деление, то при n = 2 левый и правый члены оцениваются как 3 и 2 соответственно. Структурно равные термины должны согласовываться в именах переменных.
Напротив, термин t называется переименованием или вариантом термина u, если последний возник в результате последовательного переименования всех переменных первого, т. е. если u = tσ для некоторой переименовывающей замены σ. В этом случае u также является переименованием t , поскольку замена переименования σ имеет обратную σ −1 , и t = uσ −1 . Оба термина тогда также считаются равными по модулю переименования . Во многих контекстах имена конкретных переменных в термине не имеют значения, например, аксиома коммутативности для сложения может быть сформулирована как x + y = y + x или как a + b = b + a ; в таких случаях можно переименовать всю формулу, а произвольный подтерм обычно нет, например, x + y = b + a не является допустимой версией аксиомы коммутативности. [ примечание 1 ] [ примечание 2 ]
Основные и линейные условия
[ редактировать ]Набор переменных терма t обозначается vars ( t ). Термин, который не содержит никаких переменных, называется основным термином ; термин, который не содержит нескольких вхождений переменной, называется линейным термином . Например, 2+2 является основным термином и, следовательно, также линейным термином, x ⋅( n +1) является линейным термином, n ⋅( n +1) является нелинейным термином. Эти свойства важны, например, при переписывании терминов .
Учитывая сигнатуру функциональных символов, набор всех термов образует алгебру свободных термов . Набор всех основных термов образует исходную термальную алгебру .
Сокращая количество констант как f 0 , а количество i -арных функциональных символов как fi : , количество θ h различных основных членов высотой до h можно вычислить по следующей рекурсивной формуле
- θ 0 = f 0 , поскольку основной член высоты 0 может быть только константой,
- , поскольку основной член высотой до h +1 может быть получен путем составления любых i основных членов высотой до h с использованием i -арного символа корневой функции. Сумма имеет конечное значение, если существует только конечное число констант и функциональных символов, что обычно и происходит.
Построение формул из термов
[ редактировать ]Учитывая набор R n n -арных символов отношения для каждого натурального числа n ≥ 1, атомарная формула (несортированного первого порядка) получается путем применения n -арного символа отношения к n терминам. Что касается функциональных символов, набор символов отношения R n обычно непустой только для малых n . В математической логике более сложные формулы строятся из атомарных формул с использованием логических связок и кванторов . Например, позволив обозначаем множество действительных чисел , ∀ x : x ∈ ⇒ ( x +1)⋅( x +1) ≥ 0 — математическая формула, имеющая истинное значение в алгебре комплексных чисел . Атомная формула называется основной, если она полностью построена из основных членов; все основные атомарные формулы, которые можно составить из заданного набора функций и символов-предикатов, составляют основу Эрбрана для этих наборов символов.
Операции с терминами
[ редактировать ]
- Поскольку терм имеет структуру древовидной иерархии, каждому его узлу может быть присвоена позиция или путь , то есть строка натуральных чисел, указывающая место узла в иерархии. Пустая строка, обычно обозначаемая ε, присваивается корневому узлу. Строки позиций внутри черного термина обозначены на рисунке красным.
- В каждой позиции p термина t начинается уникальный подтерм , который обычно обозначается t | п . Например, в позиции 122 черного термина на рисунке подтерм a корень имеет +2. Отношение «является подтермом» представляет собой частичный порядок в множестве термов; он рефлексивен , поскольку каждый термин тривиально является подтермом самого себя.
- Термин, полученный заменой в терме t подтерма в позиции p новым термином u, обычно обозначается t [ u ] p . Термин t [ u ] p также можно рассматривать как результат обобщенной конкатенации термина u с терминоподобным объектом t [.] ; последний называется контекстом или термином с дыркой (обозначается «.»; его позиция — p ), в которую u считается внедренным . Например, если t — черный термин на картинке, то t [ b +1] 12 приводит к члену . Последний член также является результатом встраивания термина b +1 в контекст . В неформальном смысле операции создания экземпляров и внедрения обратны друг другу: в то время как первая добавляет функциональные символы внизу термина, вторая добавляет их вверху. Упорядочение охвата связывает термин и любой результат добавления с обеих сторон.
- Каждому узлу терма может быть присвоена его глубина (некоторые авторы называют ее высотой ), т. е. расстояние (количество ребер) от корня. В этом случае глубина узла всегда равна длине его строки позиции. На рисунке уровни глубины в черном термине обозначены зеленым цветом.
- Размер . термина обычно относится к количеству его узлов или, что то же самое, к длине письменного представления термина, считая символы без круглых скобок Черный и синий термины на картинке имеют размер 15 и 5 соответственно.
- Термин u соответствует термину t , если экземпляр замены u структурно равен подтерму t , или формально, если u σ = t | p для некоторой позиции p в t и некоторой замены σ. В этом случае u , t и σ называются термином шаблона , термином субъекта и соответствующей заменой соответственно. На картинке термин синего образца соответствует черному предметному термину в позиции 1, с соответствующей заменой { x ↦ a , y ↦ a +1, z ↦ a +2 }, указанной синими переменными, немедленно оставленными их черными заменителями. Интуитивно, шаблон, за исключением его переменных, должен содержаться в субъекте; если переменная встречается в шаблоне несколько раз, в соответствующих позициях субъекта требуются равные подтермины.
- объединяющие термины
- переписывание термина
Связанные понятия
[ редактировать ]Сортированные термины
[ редактировать ]Когда область дискурса содержит элементы принципиально разных типов, полезно соответствующим образом разделить набор всех терминов. С этой целью каждой переменной и каждому константному символу присваивается сортировка (иногда также называемая типом ), а также объявление [ примечание 3 ] сортировок доменов и сортировок диапазонов для каждого функционального символа. Сортированный терм f ( t 1 ,..., t n ) может состоять из отсортированных подтермов t 1 ,..., t n только в том случае, если сорт i -го подтерма соответствует объявленному i- му доменному виду f . Такой термин еще называют хорошо отсортированным ; любой другой термин (т.е. подчиняющийся только несортированным правилам ) называется плохо отсортированным .
Например, векторное пространство имеет связанное с ним поле скалярных чисел. Пусть W и N обозначают сорт векторов и чисел соответственно, пусть V W и V N — набор векторных и числовых переменных соответственно, а C W и CN — набор векторных и числовых констант соответственно. Тогда, например и 0 ∈ CN , а сложение векторов, скалярное умножение и скалярное произведение объявляются как и соответственно. Предполагая переменные символы и a , b ∈ V N , термин хорошо отсортирован, в то время как нет (поскольку + не принимает термин типа N в качестве второго аргумента). Чтобы сделать хорошо отсортированный термин, дополнительное объявление требуется. Функциональные символы, имеющие несколько объявлений, называются перегруженными .
Дополнительную информацию см. в разделе «Множественная логика» , включая расширения описанной здесь многосортовой структуры .
Лямбда-термины
[ редактировать ]| Обозначения пример |
Граница переменные |
Бесплатно переменные |
Написано как лямбда-терм |
|---|---|---|---|
| x / n | н | х | предел (λ n . div ( x , n )) |
| я | н | сумма (1, n , λ i . степень ( i ,2)) | |
| т | а , б , к | интеграл ( а , б ,λ т . грех ( k ⋅ т )) |
Мотивация
[ редактировать ]Математические обозначения, показанные в таблице, не вписываются в схему термина первого порядка, определенную выше , поскольку все они вводят собственную локальную или связанную переменную, которая может не появляться за пределами области обозначения, например не имеет смысла. Напротив, другие переменные, называемые свободными , ведут себя как обычные переменные-члены первого порядка, например имеет смысл.
Все эти операторы можно рассматривать как принимающие в качестве одного из аргументов функцию, а не значение. Например, оператор lim применяется к последовательности, т.е. к отображению положительного целого числа, например, в действительные числа. Другой пример: функция C для реализации второго примера из таблицы, Σ, будет иметь аргумент-указатель функции (см. вставку ниже).
Лямбда-термины могут использоваться для обозначения анонимных функций, которые будут предоставляться в качестве аргументов lim , Σ, ∫ и т. д.
Например, квадрат функции из приведенной ниже программы на языке C можно анонимно записать как лямбда-терм λ i . я 2 . Тогда общий оператор суммы Σ можно рассматривать как символ троичной функции, принимающий значение нижней границы, значение верхней границы и функцию, подлежащую суммированию. Благодаря последнему аргументу оператор Σ называется функциональным символом второго порядка . Другой пример: лямбда-терм λ n . x / n обозначает функцию, которая отображает 1, 2, 3,... в x /1, x /2, x /3,... соответственно, то есть обозначает последовательность ( x /1, x / 2, х /3, ...). Оператор lim принимает такую последовательность и возвращает ее предел (если он определен).
В крайнем правом столбце таблицы показано, как каждый пример математической записи может быть представлен лямбда-термом, а также преобразованием обычных инфиксных операторов в префиксную форму.
int sum(int lwb, int upb, int fct(int)) { // implements general sum operator
int res = 0;
for (int i=lwb; i<=upb; ++i)
res += fct(i);
return res;
}
int square(int i) { return i*i; } // implements anonymous function (lambda i. i*i); however, C requires a name for it
#include <stdio.h>
int main(void) {
int n;
scanf(" %d",&n);
printf("%d\n", sum(1, n, square)); // applies sum operator to sum up squares
return 0;
}
Определение
[ редактировать ]Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( апрель 2021 г. ) |
Учитывая набор V переменных символов, набор лямбда-термов определяется рекурсивно следующим образом:
- каждый переменный символ x ∈ V является лямбда-термом;
- если x ∈ V — переменный символ, а t — лямбда-терм, то λ x . t также является лямбда-термом (абстракция);
- если t 1 и t 2 являются лямбда-терминами, то ( t 1 t 2 ) также является лямбда-термом (приложение).
В приведенных выше мотивирующих примерах также использовались некоторые константы, такие как div , power и т. д., которые, однако, не допускаются в чистом лямбда-исчислении.
Интуитивно понятно, что абстракция λ x . t обозначает унарную функцию, которая возвращает t при задании x , а приложение ( t 1 t 2 ) обозначает результат вызова функции t 1 с входными данными t 2 . Например, абстракция λ x . x обозначает тождественную функцию, а λ x . y обозначает постоянную функцию, всегда возвращающую y . Лямбда-терм λ x .( x x ) принимает функцию x и возвращает результат применения x к самому себе.
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Поскольку атомарные формулы тоже можно рассматривать как деревья, а переименование, по сути, является концепцией деревьев, атомарные (и, в более общем смысле, не содержащие кванторов ) формулы можно переименовывать так же, как и термины. Фактически, некоторые авторы рассматривают формулу без кванторов как термин (типа bool, а не, например, int , см. #Сортированные термины ниже).
- ^ Переименование аксиомы коммутативности можно рассматривать как альфа-преобразование универсального замыкания аксиомы: « x + y = y + x » на самом деле означает «∀ x , y : x + y = y + x », что является синонимом to «∀ a , b : a + b = b + a »; см. также термины #Lambda ниже.
- ^ То есть «тип символа» в разделе «Многосортированные подписи» статьи «Подпись (логика)».
Ссылки
[ редактировать ]- Франц Баадер ; Тобиас Нипков (1999). Переписывание терминов и все такое . Издательство Кембриджского университета. стр. 1–2 и 34–35. ISBN 978-0-521-77920-3 .
- ^ Си Чанг ; Х. Джером Кейслер (1977). Теория моделей . Исследования по логике и основам математики. Том. 73. Северная Голландия. ; здесь: Раздел 1.3
- ^ Гермес, Ганс (1973). Введение в математическую логику . Спрингер Лондон. ISBN 3540058192 . ISSN 1431-4657 . ; здесь: Раздел II.1.3






















