Заблуждение игрока

, Заблуждение игрока также известное как ошибка Монте-Карло или ошибка зрелости шансов , заключается в убеждении, что, если событие (чьи события независимы и одинаково распределены ) происходит реже, чем ожидалось, оно с большей вероятностью произойдет. снова в будущем (или наоборот). Заблуждение азартными обычно связано с играми , когда, например, можно полагать, что при следующем броске костей с большей вероятностью выпадет шесть, чем обычно, потому что в последнее время выпало меньше ожидаемого шестерок .

Термин «заблуждение Монте-Карло» возник на примере явления, когда колесо рулетки вращалось черным 26 раз подряд в казино Монте-Карло в 1913 году.

Примеры

Подбрасывание монеты

Со временем соотношение подбрасываний красной/синей монеты приближается к 50-50, но разница бессистемно снижается до нуля.

Заблуждение игрока можно проиллюстрировать, рассмотрев неоднократное подбрасывание честной монеты . Исходы различных бросков статистически независимы , а вероятность выпадения орла при одном броске равна ⁠ 1/2 ⁠ ( . один из двух) Вероятность выпадения двух орлов при двух бросках равна ⁠ 1/4 один из четырёх) , ( ⁠ а вероятность выпадения трёх орлов за три броска равна ⁠ 1/8 ⁠ ( . один из восьми) В общем случае, если A _i — это событие, когда при броске i честной монеты выпал орел, то:

$\Pr \left(\bigcap _{i=1}^{n}A_{i}\right)=\prod _{i=1}^{n}\Pr(A_{i})={1 \over 2^{n}}$.

Если после выпадения четырех орлов подряд при следующем броске монеты также выпадет орел, это завершит серию из пяти последовательных орлов. Поскольку вероятность выпадения пяти последовательных орлов равна ⁠ 1/32 (один из тридцати двух), человек может поверить , что при ⁠ следующем броске с большей вероятностью снова выпадет решка, а не орел. Это неверно и является примером заблуждения игрока. Событие «5 орлов подряд» и событие «сначала 4 орла, потом решка» равновероятны, каждое из которых имеет вероятность ⁠ 1/32 ​ ​ ⁠ . Поскольку при первых четырех бросках выпадает решка, вероятность того, что при следующем броске выпадет решка, равна:

$\Pr \left(A_{5}|A_{1}\cap A_{2}\cap A_{3}\cap A_{4}\right)=\Pr \left(A_{5}\right)={\frac {1}{2}}$.

Хотя серия из пяти орлов имеет вероятность ⁠ 1/32 = 0,03125 ( только ⁠ чуть больше 3%), недоразумение заключается в непонимании того, что это так до того, как будет подброшена первая монета . После первых четырех бросков в этом примере результаты уже не являются неизвестными, поэтому их вероятности в этот момент равны 1 (100%). Вероятность того, что серия подбрасываний монеты любой длины продолжится еще одним подбрасыванием, всегда равна 0,5. Рассуждение о том, что пятый бросок, скорее всего, окажется решкой, потому что предыдущие четыре броска были решкой, а удача в прошлом повлияла на шансы в будущем, составляет основу заблуждения.

Почему вероятность честной монеты равна 1/2

Если честную монету подбросить 21 раз, вероятность выпадения 21 орла равна 1 из 2 097 152. Вероятность выпадения орла после того, как он уже выкинул 20 орлов подряд, равна ⁠ 1/2 ​ ⁠ ​ . Предполагая честную монету:

• Вероятность выпадения 20 орлов и 1 решки равна 0,5. ²⁰ × 0.5 = 0.5 ²¹
• Вероятность того, что выпадет 20 орлов, то 1 орел равна 0,5. ²⁰ × 0.5 = 0.5 ²¹

Вероятность того, что выпадет 20 орлов, а затем одна решка, и вероятность того, что выпадет 20 орлов, а затем еще одна решка, равны 1 из 2 097 152. Если подбросить честную монету 21 раз, то с равной вероятностью выпадет 21 орел, 20 орел и затем 1 решка. Эти два результата столь же вероятны, как и любая другая комбинация, которую можно получить при 21 подбрасывании монеты. Все комбинации из 21 броска будут иметь вероятность, равную 0,5. ²¹ или 1 из 2 097 152. Предположение, что изменение вероятности произойдет в результате результата предыдущих бросков, неверно, поскольку каждый результат последовательности из 21 броска столь же вероятен, как и другие результаты. В соответствии с теоремой Байеса вероятным результатом каждого подбрасывания является вероятность выпадения честной монеты, которая равна ⁠ 1 / 2 ⁠ .

Другие примеры

Это заблуждение приводит к неправильному представлению о том, что предыдущие неудачи повысят вероятность успеха последующих попыток. Для честного 16-гранного кубика вероятность выпадения каждого исхода равна ⁠ 1/16 ⁠ 6,25% ) ( . Если выигрыш определяется как выпадение 1, вероятность того, что 1 выпадет хотя бы один раз из 16 бросков, равна:

$1-\left[{\frac {15}{16}}\right]^{16}\,=\,64.39\%$

Вероятность проигрыша при первом броске равна ⁠ 15/16 ⁠ 93,75% ) ( . Согласно заблуждению, у игрока должны быть более высокие шансы на победу после того, как произошел один проигрыш. Вероятность хотя бы одного выигрыша теперь равна:

$1-\left[{\frac {15}{16}}\right]^{15}\,=\,62.02\%$

Проиграв один бросок, вероятность выигрыша игрока снижается на два процентных пункта. Если осталось 5 проигрышей и 11 бросков, вероятность выигрыша падает примерно до 0,5 (50%). Вероятность хотя бы одного выигрыша не увеличивается после серии проигрышей; на самом деле вероятность успеха фактически снижается , потому что остается меньше испытаний, в которых можно победить. Вероятность выигрыша в конечном итоге будет равна вероятности выигрыша в одном броске, что ⁠ 1/16 происходит , (6,25%) и ⁠ когда остался только один бросок.

Обратное положение

После устойчивой тенденции к выпадению решки игрок может также решить, что решка стала более вероятным исходом. Это рациональный и байесовский вывод, принимая во внимание возможность того, что монета может быть нечестной; это не заблуждение. Полагая, что шансы в пользу решки, игрок не видит причин переходить на решку. Однако ошибочно считать, что последовательность испытаний хранит в себе память о прошлых результатах, которая имеет тенденцию благоприятствовать или препятствовать будущим результатам.

Обратное заблуждение игрока, описанное Яном Хакингом, представляет собой ситуацию, когда игрок, входящий в комнату и видящий, как человек бросает двойную шестерку на паре игральных костей, может ошибочно заключить, что этот человек, должно быть, бросал кости в течение довольно долгого времени, как они бы это сделали. вряд ли наберут двойную шестерку с первой попытки.

Ретроспективная ошибка игрока

Исследователи изучили, существует ли подобная предвзятость для выводов о неизвестных прошлых событиях, основанных на известных последующих событиях, назвав это «заблуждением ретроспективного игрока».

Примером ошибки ретроспективного игрока может быть наблюдение нескольких последовательных «орлов» при подбрасывании монеты и вывод из этого, что ранее неизвестный бросок был «решкой». Утверждалось, что реальные примеры ретроспективной ошибки игрока существуют в таких событиях, как происхождение Вселенной . В своей книге «Вселенные » Джон Лесли утверждает, что «наличие огромного количества вселенных, очень разных по своим характеристикам, может быть нашим лучшим объяснением того, почему по крайней мере одна вселенная имеет характер, допускающий жизнь». Дэниел М. Оппенгеймер и Бенуа Монен утверждают, что «другими словами,« лучшее объяснение »события с низкой вероятностью состоит в том, что это всего лишь одно из множества испытаний, что является основной интуицией ошибки обратного игрока». Продолжаются философские споры о том, являются ли такие аргументы заблуждением, утверждая, что возникновение нашей Вселенной ничего не говорит о существовании других вселенных или испытаниях вселенных. Три исследования с участием студентов Стэнфордского университета проверили существование ретроспективного заблуждения игроков. Все три исследования пришли к выводу, что люди ошибаются как в ретроспективе, так и в отношении будущих событий. Авторы всех трех исследований пришли к выводу, что их результаты имеют значительные « методологические последствия», но могут также иметь «важные теоретические последствия», которые требуют изучения и исследования, заявив, что «[] тщательное понимание таких процессов рассуждения требует, чтобы мы не только изучали, как они влияют на наши предсказания будущего, но и наше восприятие прошлого».

Роды

В 1796 году Пьер-Симон Лаплас описал в «Философском очерке о вероятностях» способы, с помощью которых люди рассчитывали вероятность рождения сыновей: «Я видел людей, страстно желавших иметь сына, которые могли учиться только с тревогой по поводу рождения мальчиков. в том месяце, когда они ожидали стать отцами, полагая, что соотношение этих рождений к числу девочек должно быть одинаковым в конце каждого месяца, они пришли к выводу, что уже родившиеся мальчики сделают более вероятным рождение следующих девочек. " Будущие отцы опасались, что если в окружающей общине родится больше сыновей, то у них самих будет больше шансов родить дочь. Это эссе Лапласа считается одним из самых ранних описаний заблуждения. Аналогичным образом, имея несколько детей одного пола, некоторые родители могут ошибочно полагать, что у них должен родиться ребенок противоположного пола.

Казино Монте-Карло

Пример заблуждения игрока произошел во время игры в рулетку в казино Монте-Карло 18 августа 1913 года, когда шарик выпал черным 26 раз подряд. Это был крайне маловероятный случай: вероятность того, что последовательность красного или черного цвета выпадет 26 раз подряд, равна ( ⁠ 18 / 37 ⁠ ) ^26-1 или около 1 из 66,6 миллиона, если предположить, что механизм объективен. Игроки потеряли миллионы франков, делая ставки против черного цвета, ошибочно полагая, что эта полоса вызывает дисбаланс в случайности колеса и что за ней должна следовать длинная красная полоса.

Непримеры

Ненезависимые события

Заблуждение игрока неприменимо, когда вероятность различных событий не является независимой . В таких случаях вероятность будущих событий может меняться в зависимости от результатов прошлых событий, например, в результате статистической перестановки событий. Примером может служить случай, когда карты вытягиваются из колоды без замены. Если из колоды вытянут туз и не вставлен повторно, следующая вытянутая карта с меньшей вероятностью будет тузом и с большей вероятностью будет другого ранга. Вероятность вытянуть еще один туз, если предположить, что это была первая вытянутая карта и что джокеров нет , уменьшилась с ⁠ 4 / 52 ⁠ (7,69%) до ⁠ 3 / 51 ⁠ (5,88%), при этом вероятность каждого другого ранга увеличилась с ⁠ 4 / 52 ⁠ (7,69%) до ⁠ 4/51 ⁠ 7,84% ) ( . Этот эффект позволяет системам подсчета карт работать в таких играх, как блэкджек .

Предвзятость

В большинстве иллюстраций заблуждения игрока и обратного заблуждения игрока предполагается, что испытание (например, подбрасывание монеты) является справедливым. На практике это предположение может не выполняться. Например, если монету подбросить 21 раз, вероятность того, что на честной монете выпадет 21 орел, равна 1 из 2 097 152. Поскольку эта вероятность очень мала, если это произойдет, вполне может быть, что монета каким-то образом смещена в сторону падения орла, или что она контролируется скрытыми магнитами или чем-то подобным. В этом случае разумной ставкой будет «орёл», потому что байесовский вывод на основе эмпирических данных — 21 орел подряд — предполагает, что монета, скорее всего, будет смещена в сторону орла. Байесовский вывод можно использовать, чтобы показать, что долгосрочная пропорция различных результатов неизвестна, но может быть заменена (это означает, что случайный процесс, в результате которого генерируются результаты, может быть смещенным, но с равной вероятностью будет смещенным в любом направлении) и что предыдущие наблюдения демонстрируют вероятное направление систематической ошибки, результат, который чаще всего возникал в наблюдаемых данных, с наибольшей вероятностью произойдет снова.

Например, если априорная вероятность смещенной монеты составляет, скажем, 1%, и если предположить, что такая смещенная монета выпадет орлом, скажем, в 60% случаев, то после 21 орла вероятность смещенной монеты увеличится примерно до 32. %.

В первой сцене пьесы Розенкранц и Гильденстерн мертвы» « Тома Стоппарда эти проблемы обсуждаются, поскольку один человек постоянно меняет головы, а другой рассматривает различные возможные объяснения.

Изменение вероятностей

Если позволить внешним факторам изменить вероятность событий, ошибка игрока может не состояться. Например, изменение правил игры может дать преимущество одному игроку перед другим, что повысит его или ее процент побед. Точно так же успех неопытного игрока может снизиться после того, как команды соперников узнают об их слабостях и начнут играть против них. Это еще один пример предвзятости.

Психология

Происхождение

Заблуждение игрока возникает из-за веры в закон малых чисел , что приводит к ошибочному убеждению, что небольшие выборки должны быть репрезентативными для большей популяции. Согласно этому заблуждению, полосы должны в конечном итоге выровняться, чтобы быть репрезентативными. Амос Тверски и Дэниел Канеман впервые предположили, что ошибка игрока — это когнитивное предубеждение, вызванное психологической эвристикой, называемой эвристикой репрезентативности , которая утверждает, что люди оценивают вероятность определенного события, оценивая, насколько оно похоже на события, которые они пережили раньше, и насколько похожи события, окружающие эти два процесса. Согласно этой точке зрения, «например, после наблюдения длинной серии красных цветов на рулетке, большинство людей ошибочно полагают, что черный цвет приведет к более репрезентативной последовательности, чем появление дополнительного красного цвета». поэтому люди ожидают, что краткосрочный период случайных результатов должен обладать свойствами более длительного периода, в частности, в том, что отклонения от среднего должны уравновешиваться. Когда людей просят составить случайную последовательность подбрасываний монеты, они склонны составлять последовательности, в которых соотношение орла к решке в любом коротком сегменте остается ближе к 0,5, чем можно было бы предсказать случайно. Это явление известно как нечувствительность к выборке. размер . Канеман и Тверски интерпретируют это так, что люди верят, что короткие последовательности случайных событий должны быть репрезентативными для более длинных. Эвристика репрезентативности также упоминается в основе родственного феномена иллюзии кластеризации , согласно которому люди воспринимают полосы случайных событий как неслучайные, тогда как на самом деле вероятность возникновения таких полос в небольших выборках гораздо выше, чем люди ожидают.

Заблуждение игрока также можно объяснить ошибочным убеждением, что азартные игры или даже случайность сама по себе являются справедливым процессом, который может исправиться в случае полос, известных как гипотеза справедливого мира . Другие исследователи полагают, что вера в эту ошибку может быть результатом ошибочной веры во внутренний локус контроля . Когда человек считает, что результаты азартных игр являются результатом его собственных навыков, он может быть более восприимчив к заблуждению игрока, поскольку отвергает идею о том, что случай может превзойти навыки или талант.

Вариации

Некоторые исследователи полагают, что можно выделить два типа заблуждений игрока: первый тип и второй тип. Первый тип — это классическое заблуждение игрока, когда люди полагают, что определенный результат наступает после длинной серии других результатов. Заблуждение игрока второго типа, по определению Гидеона Керена и Чарльза Льюиса, возникает, когда игрок недооценивает количество наблюдений, необходимых для определения благоприятного результата, например, он наблюдает за колесом рулетки в течение определенного периода времени, а затем делает ставку на числа, которые кажутся наиболее вероятными. часто. Для событий с высокой степенью случайности обнаружение систематической ошибки, которая приведет к благоприятному исходу, занимает непрактично большое количество времени и сделать это очень сложно, если вообще возможно. Эти два типа различаются тем, что первый тип ошибочно предполагает, что условия азартных игр являются справедливыми и идеальными, а второй тип предполагает, что условия являются предвзятыми и что эта предвзятость может быть обнаружена через определенное время.

Другая разновидность, известная как ошибка ретроспективного игрока, возникает, когда люди считают, что, казалось бы, редкое событие должно произойти из более длинной последовательности, чем более распространенное событие. Убеждение в том, что воображаемая последовательность бросков кубика более чем в три раза длиннее, когда наблюдается набор из трех шестерок, а не когда есть только две шестерки. Этот эффект может наблюдаться в единичных случаях или даже последовательно. Другой пример — услышать, что подросток занимался незащищенным сексом и забеременела в данную ночь, и сделать вывод, что она занималась незащищенным сексом дольше, чем если бы мы слышали, что она занималась незащищенным сексом, но не забеременела, когда вероятность забеременеть беременность в результате каждого полового акта не зависит от продолжительности предыдущего полового акта.

Связь с заблуждением горячей руки

Другая психологическая точка зрения гласит, что ошибку игрока можно рассматривать как аналог ошибки «горячей руки» в баскетболе , при которой люди склонны предсказывать тот же результат, что и предыдущее событие (известное как положительная недавность), что приводит к убеждению, что игрок, набравший больше очков, будет продолжать играть. счет. Заблуждение игрока заключается в том, что люди предсказывают результат, противоположный предыдущему событию – отрицательную давность – полагая, что, поскольку колесо рулетки в предыдущих шести случаях выпадало на черное, в следующем оно должно выпасть на красное. Эйтон и Фишер предположили, что люди проявляют положительную новизну к ошибке «горячей руки», потому что ошибка связана с человеческими действиями, и что люди не верят, что неодушевленный объект может стать «горячим». Действия человека не воспринимаются как случайные, и люди с большей вероятностью продолжат серию последовательных результатов, если верят, что процесс, генерирующий результаты, неслучайен. Когда человек демонстрирует ошибку игрока, он с большей вероятностью проявит также ошибку «горячей руки», что позволяет предположить, что за два заблуждения ответственна одна конструкция.

Разница между этими двумя заблуждениями также обнаруживается в процессе принятия экономических решений. В исследовании Хубера, Кирхлера и Стокля, проведенном в 2010 году, изучалось, как на финансовом рынке проявляются «горячая рука» и ошибка игрока. Исследователи предоставили своим участникам выбор: они могли либо сделать ставку на результат серии подбрасываний монеты, использовать мнение эксперта, чтобы повлиять на их решение, либо вместо этого выбрать безрисковую альтернативу за меньшее финансовое вознаграждение. Участники обратились к мнению экспертов, чтобы принять решение в 24% случаев, основываясь на своем прошлом опыте успеха, что является примером «горячей руки». Если эксперт был прав, 78% участников снова выбирали мнение эксперта, в отличие от 57%, когда эксперт ошибался. Участники также продемонстрировали ошибку игрока: их выбор «орел» или «решка» уменьшился после того, как они заметили серию результатов в любом исходе. Этот эксперимент помог укрепить теорию Эйтона и Фишера о том, что люди больше доверяют человеческим действиям, чем кажущимся случайным процессам.

Нейрофизиология

Хотя эвристика репрезентативности и другие когнитивные искажения являются наиболее часто упоминаемой причиной заблуждения игрока, исследования показывают, что здесь может быть и неврологический компонент. Функциональная магнитно-резонансная томография показала, что после проигрыша в пари или азартной игре (так называемая потеря риска) активируется лобно-теменная сеть мозга, что приводит к более рисковому поведению. Напротив, наблюдается снижение активности миндалевидного тела , хвостатого тела и вентрального полосатого тела после потери риска . Активация миндалевидного тела отрицательно коррелирует с заблуждением игрока, так что чем больше активности проявляется в миндалевидном теле, тем меньше вероятность того, что человек станет жертвой заблуждения игрока. Эти результаты показывают, что ошибка игрока больше зависит от префронтальной коры головного мозга , которая отвечает за исполнительные , целенаправленные процессы, и меньше от областей мозга, которые контролируют принятие эмоциональных решений.

Желание продолжать играть в азартные игры или делать ставки контролируется полосатым телом , которое поддерживает метод обучения на основе выбора и результата. Полосатое тело обрабатывает ошибки прогнозирования, и поведение соответственно меняется. После победы положительное поведение подкрепляется , а после проигрыша поведение обуславливается тем, что его следует избегать. У людей, проявляющих ошибку игрока, этот метод выбора и результата нарушен, и они продолжают рисковать после серии проигрышей.

Возможные решения

Заблуждение игрока — это глубоко укоренившееся когнитивное предубеждение, и его очень трудно преодолеть. Обучение людей природе случайности не всегда оказывается эффективным в уменьшении или устранении любого проявления заблуждения. Участникам исследования Бича и Свенсона в 1967 году показали перетасованную колоду учетных карточек с фигурами на них и попросили угадать, какая фигура будет следующей в последовательности. Экспериментальную группу участников проинформировали о природе и существовании заблуждения игрока, и им было дано четкое указание не полагаться на зависимость от бега при построении своих предположений. Контрольной группе этой информации не предоставили. Стили ответов двух групп были схожими, что указывает на то, что экспериментальная группа по-прежнему основывала свой выбор на продолжительности последовательности пробежек. Это привело к выводу, что информирования людей о случайности недостаточно для уменьшения заблуждения игрока.

Восприимчивость человека к заблуждениям игрока может уменьшаться с возрастом. В исследовании, проведенном Фишбейном и Шнархом в 1997 году, анкеты были предложены пяти группам: учащимся 5, 7, 9, 11 классов и студентам колледжей, специализирующимся на преподавании математики. Ни один из участников не получил никакого предварительного образования в отношении вероятности. Заданный вопрос был следующим: «Ронни подбросил монету три раза, и во всех случаях выпал орел. Ронни намеревается подбросить монету еще раз. Каков шанс, что в четвертый раз выпадет орел?» Результаты показали, что по мере того, как студенты становились старше, вероятность того, что они ответят «меньше, чем вероятность выпадения решки», уменьшалась, что указывало на отрицательный эффект новизны. Эффект отрицательного новизны наблюдался у 35% пятиклассников, 35% семиклассников и 20% девятиклассников. Так ответили только 10% одиннадцатиклассников и никто из студентов колледжа. Фишбейн и Шнарх предположили, что склонность человека полагаться на эвристику репрезентативности и другие когнитивные искажения можно преодолеть с возрастом.

Другое возможное решение предлагают Рони и Трик, гештальт- психологи, которые предполагают, что ошибку можно устранить в результате группировки. Когда будущее событие, такое как подбрасывание монеты, описывается как часть последовательности, независимо от того, насколько произвольно, человек автоматически будет рассматривать это событие в его связи с прошлыми событиями, что приводит к ошибке игрока. Когда человек считает каждое событие независимым, ошибка может быть значительно уменьшена.

Рони и Трик сказали участникам эксперимента, что они делают ставку либо на два блока по шесть бросков монеты, либо на два блока по семь бросков монеты. Четвертый, пятый и шестой броски имели одинаковый результат: либо три орла, либо три решки. Седьмой бросок был сгруппирован либо с концом одного блока, либо с началом следующего блока. Участники продемонстрировали сильнейшее заблуждение игрока, когда седьмое испытание было частью первого блока, сразу после последовательности «орел или решка». Исследователи отметили, что участники, которые не продемонстрировали ошибку игрока, проявили меньшую уверенность в своих ставках и делали ставки меньшее количество раз, чем участники, сделавшие выбор с ошибкой игрока. Когда седьмая попытка была сгруппирована со вторым блоком и воспринималась как не являющаяся частью серии, ошибка игрока не произошла.

Рони и Трик утверждали, что вместо того, чтобы учить людей природе случайности, этой ошибки можно избежать, научив людей относиться к каждому событию так, как если бы оно было началом, а не продолжением предыдущих событий. Они предположили, что это помешает людям играть в азартные игры, когда они проигрывают, в ошибочной надежде, что их шансы на выигрыш увеличиваются в результате взаимодействия с предыдущими событиями.

Пользователи

Типы пользователей

В реальных условиях многочисленные исследования показали, что для различных лиц, принимающих решения, находящихся в сценариях с высокими ставками, вполне вероятно, что они будут отражать некоторую степень сильной отрицательной автокорреляции в своих суждениях.

Судьи по вопросам убежища

В исследовании, целью которого было выяснить, существует ли отрицательная автокорреляция, существующая с заблуждением игрока, в решении, принятом американскими судьями по предоставлению убежища, результаты показали, что после двух последовательных предоставлений убежища вероятность одобрения третьего разрешения у судьи будет на 5,5% меньше.

Бейсбольные судьи

В игре в бейсбол решения принимаются каждую минуту. Одним из конкретных решений, принимаемых судьями , которое часто подвергается тщательному анализу, является решение о «зоне удара». Всякий раз, когда бьющий не замахивается, судья должен решить, находился ли мяч в пределах справедливой для бьющего зоны, известной как зона удара . Если мяч находится за пределами этой зоны, мяч не засчитывается в счет аута бьющего. Результаты исследования более 12 000 игр показали, что судьи на 1,3% реже объявляют страйк, если предыдущие два мяча также были страйками.

Кредитные специалисты

При принятии решений кредитными специалистами можно утверждать, что денежные стимулы являются ключевым фактором в принятии предвзятых решений, что затрудняет изучение эффекта ошибки игрока. Однако исследования показывают, что кредитные специалисты, которые не заинтересованы в денежной выгоде, на 8% менее склонны одобрить кредит, если они одобрили его для предыдущего клиента.

Лотерейные игроки

Влияние заблуждения игрока на выбор лотереи, на основе исследований Дека Террелла. После того, как выпали выигрышные номера, игроки в лотерею в ответ сокращают количество раз, когда они выбирают эти номера в следующих тиражах. Этот эффект постепенно исправляется с течением времени, поскольку игроки меньше подвержены влиянию ошибки.

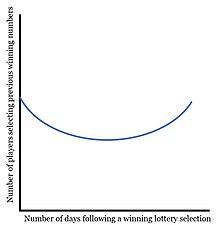
Лотереи и джекпоты привлекают игроков по всему миру, и самым важным решением для многообещающих победителей является то, какие числа выбрать. Хотя у большинства людей будет своя собственная стратегия, данные показывают, что после того, как число будет выбрано в качестве победителя в текущем розыгрыше, количество исходов этого же числа в следующей лотерее значительно упадет. Популярное исследование, проведенное Чарльзом Клотфелтером и Филипом Куком в 1991 году, изучало этот эффект и пришло к выводу, что игроки перестанут выбирать номера сразу после того, как они были выбраны, что в конечном итоге восстановит популярность выбора в течение трех месяцев. Вскоре после этого в 1994 году Дек Террелл провел исследование, чтобы проверить выводы Клотфелтера и Кука. Ключевым изменением в исследовании Террелла стало изучение лотереи тотализатора , в которой выбранное число с меньшими общими ставками приведет к более высокой выплате. Хотя это исследование и пришло к выводу, что игроки в обоих типах лотерей демонстрируют поведение, соответствующее теории заблуждения игрока, те, кто принимал участие в пари-взаимных ставках, похоже, подверглись меньшему влиянию.

Таблица 1. Процентное изменение чисел, выбранных игроками в лотерею, на основе Clotfelter, Cook (1991)

		Сумма ставки игроков в лотерею
Номера разыграны 14 апреля 1988 г.		День розыгрыша	Дни после розыгрыша
апрель	Номера победителей	0	1	3	7	56
11	244	41	34	24	27	30
12	504	29	20	12	18	15
13	718	28	20	17	19	25
14	323	134	95	79	81	76
15	640	10	20	18	16	20
16	957	30	22	20	24	32
Средний процент игроков, выбравших ранее выигрышные номера по сравнению со днем ​​розыгрыша			78%	63%	68%	73%

Эффект ошибки игрока можно наблюдать, поскольку числа выбираются гораздо реже вскоре после того, как они выбраны в качестве победителей, и медленно восстанавливаются в течение двухмесячного периода. Например, 11 апреля 1988 года 41 игрок выбрал в качестве выигрышной комбинации 244. Три дня спустя только 24 человека выбрали 244, что на 41,5% меньше. Это заблуждение игрока в действии, поскольку игроки в лотерею полагают, что появление выигрышной комбинации в предыдущие дни снизит вероятность ее появления сегодня.

Игроки в видеоигры

В некоторых видеоиграх используются лутбоксы — набор внутриигровых предметов, которые можно получить при открытии, со случайным содержимым, определяемым показателями редкости в качестве схемы монетизации . Примерно с 2018 года лутбоксы оказались под пристальным вниманием правительств и правозащитников на том основании, что они сродни азартным играм, особенно в отношении игр, ориентированных на молодежь. В некоторых играх используется специальный механизм «таймера жалости», который заключается в том, что если игрок открыл несколько ящиков с добычей подряд, не получив предмет высокой редкости, последующие ящики с добычей улучшат шансы на выпадение предмета с более высокой вероятностью. Считается, что это способствует заблуждению игрока, поскольку оно укрепляет идею о том, что игрок в конечном итоге получит предмет высокой редкости (выигрыш) после получения только обычных предметов из ряда предыдущих ящиков с добычей.

См. также

• Эвристика доступности
• Тщеславие игрока
• разорение игрока
• Обратное заблуждение игрока
• Заблуждение «горячей руки»
• Закон средних чисел
• Мартингейл (система ставок)
• Возврат к среднему значению (финансы)
• Безпамять
• Оскар
• Регрессия к среднему значению
• Статистическая закономерность
• Проблемы с азартными играми