Частично заказанный комплект

показывать Транзитивные   бинарные отношения
Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Total, Semiconnex Anti- reflexive Equivalence relation Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Preorder (Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Partial order ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Total preorder ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Total order ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Prewellordering ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Well-quasi-ordering ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Well-ordering ✗ Y Y Y ✗ ✗ Y ✗ ✗ Lattice ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-semilattice ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Meet-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Strict partial order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict weak order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict total order ✗ Y Y ✗ ✗ ✗ ✗ Y Y Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Definitions, for all $a,b$ and $S\neq \varnothing :$ ${\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}$ ${\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}$ ${\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}$ ${\begin{aligned}\min S\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}$ $aRa$ ${\text{not }}aRa$ ${\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}$
Y indicates that the column's property is always true the row's term (at the very left), while ✗ indicates that the property is not guaranteed in general (it might, or might not, hold). For example, that every equivalence relation is symmetric, but not necessarily antisymmetric, is indicated by Y in the "Symmetric" column and ✗ in the "Antisymmetric" column, respectively. All definitions tacitly require the homogeneous relation $R$ be transitive: for all $a,b,c,$ if $aRb$ and $bRc$ then $aRc.$ A term's definition may require additional properties that are not listed in this table.

Рис. 1. Диаграмма Хассе множества всех подмножеств трехэлементного множества. $\{x,y,z\},$ упорядочено по включению . Множества, соединенные восходящим путем, например $\emptyset$ и $\{x,y\}$, сопоставимы, а, например, $\{x\}$ и $\{y\}$ нет.

В математике , особенно в теории порядка , частичный порядок множества — это такое расположение, при котором для определенных пар элементов один предшествует другому. Слово «частичный» используется для обозначения того, что не каждая пара элементов должна быть сопоставима; то есть могут существовать пары, в которых ни один элемент не предшествует другому. Таким образом, частичные заказы обобщают общие заказы , в которых каждая пара сопоставима.

Формально частичный порядок — это однородное бинарное отношение , которое является рефлексивным , антисимметричным и транзитивным . Частично упорядоченный набор ( Посет ») — это упорядоченная пара. сокращенно « $P=(X,\leq )$ состоящий из набора $X$ (называемый набором основным $P$) и частичный порядок $\leq$ на $X$. Когда значение ясно из контекста и нет никакой двусмысленности относительно частичного порядка, набор $X$ сам иногда называют посетом.

Отношения частичного порядка

Термин «частичный порядок» обычно относится к рефлексивным отношениям частичного порядка, называемым в этой статье нестрогим частичным порядком. Однако некоторые авторы используют этот термин для обозначения другого распространенного типа отношений частичного порядка — иррефлексивных отношений частичного порядка, также называемых строгими отношениями частичного порядка. Строгий и нестрогий частичный порядок можно поставить во взаимно однозначное соответствие , поэтому для каждого строгого частичного порядка существует уникальный соответствующий нестрогий частичный порядок, и наоборот.

Частичные заказы

Рефлекторный ​ , слабый , или нестрогий частичный порядок , обычно называемый просто частичным порядком , представляет собой однородное отношение ≤ на множестве $P$ это рефлексивно , антисимметрично и транзитивно . То есть для всех $a,b,c\in P,$ он должен удовлетворять:

1. Рефлексивность : $a\leq a$, т.е. каждый элемент связан сам с собой.
2. Антисимметрия : если $a\leq b$ и $b\leq a$ затем $a=b$, т.е. никакие два отдельных элемента не предшествуют друг другу.
3. Транзитивность : если $a\leq b$ и $b\leq c$ затем $a\leq c$.

Нестрогий частичный порядок также известен как антисимметричный предварительный порядок .

Строгие частичные заказы

Невозмутимый ​ , сильный , или строгий частичный порядок — это однородное отношение < на множестве $P$ это иррефлексивно , асимметрично и транзитивно ; то есть он удовлетворяет следующим условиям для всех $a,b,c\in P:$

1. Иррефлексивность : $\neg \left(a<a\right)$, т.е. ни один элемент не связан сам с собой (также называемый антирефлексивным).
2. Асимметрия : если $a<b$ тогда нет $b<a$.
3. Транзитивность : если $a<b$ и $b<c$ затем $a<c$.

Иррефлексивность и транзитивность вместе подразумевают асимметрию. Кроме того, асимметрия подразумевает иррефлексивность. Другими словами, транзитивное отношение асимметрично тогда и только тогда, когда оно иррефлексивно. Таким образом, определение остается тем же, если оно опускает либо иррефлексивность, либо асимметрию (но не то и другое одновременно).

Строгий частичный порядок также известен как асимметричный строгий предварительный порядок .

Соответствие строгих и нестрогих отношений частичного порядка.

Рис. 2 Коммутативная диаграмма связей между строгими/нестрогими отношениями и их двойниками посредством операций рефлексивного замыкания ( cls ), иррефлексивного ядра ( ker ) и обратного отношения ( cnv ). Каждое отношение изображается своей логической матрицей для ЧУ-множества, диаграмма Хассе которого изображена в центре. Например $3\not \leq 4$ поэтому строка 3 и столбец 4 нижней левой матрицы пусты.

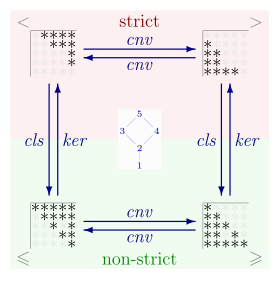
Строгие и нестрогие частичные порядки на множестве. $P$ тесно связаны. Нестрогий частичный порядок $\leq$ может быть преобразован в строгий частичный порядок путем удаления всех отношений вида $a\leq a;$ то есть строгий частичный порядок — это множество $<\;:=\ \leq \ \setminus \ \Delta _{P}$ где $\Delta _{P}:=\{(p,p):p\in P\}$ тождественное отношение на $P\times P$ и $\;\setminus \;$ обозначает вычитание множества . И наоборот, строгий частичный порядок < на $P$ может быть преобразован в нестрогий частичный порядок путем присоединения всех отношений этой формы; то есть, $\leq \;:=\;\Delta _{P}\;\cup \;<\;$ является нестрогим частичным порядком. Таким образом, если $\leq$ является нестрогим частичным порядком, то соответствующий строгий частичный порядок < является иррефлексивным ядром , заданным формулой $$a<b{\text{ if }}a\leq b{\text{ and }}a\neq b.$$И наоборот, если < — строгий частичный порядок, то соответствующий нестрогий частичный порядок $\leq$ это рефлексивное закрытие, определяемое: $$a\leq b{\text{ if }}a<b{\text{ or }}a=b.$$

Двойные заказы

Основная статья: Двойственность (теория порядка)

Двойной или ( противоположный ) $R^{\text{op}}$ отношения частичного порядка $R$ определяется путем разрешения $R^{\text{op}}$ быть обратным отношением $R$, то есть $xR^{\text{op}}y$ тогда и только тогда, когда $yRx$. Двойственным нестрогому частичному порядку является нестрогий частичный порядок, а двойник строгого частичного порядка является строгим частичным порядком. Двойственное к двойственному отношению является исходным отношением.

Обозначения

Учитывая набор $P$ и отношение частичного порядка, обычно нестрогий частичный порядок $\leq$, мы можем однозначно расширить наши обозначения, чтобы определить четыре отношения частичного порядка $\leq ,$ $<,$ $\geq ,$ и $>$, где $\leq$ является нестрогим отношением частичного порядка на $P$, $<$ — ассоциированное строгое отношение частичного порядка на $P$ ( иррефлексивное ядро $\leq$), $\geq$ является двойником $\leq$, и $>$ является двойником $<$. Строго говоря, термин «частично упорядоченное множество» относится к множеству, в котором все эти отношения определены соответствующим образом. Но на практике достаточно рассмотреть только одно отношение: $(P,\leq )$ или $(P,<)$или, в редких случаях, нестрогие и строгие отношения вместе, $(P,\leq ,<)$.

Термин «упорядоченный набор» иногда используется как сокращение от частично упорядоченного набора , если из контекста ясно, что никакой другой вид порядка не подразумевается. В частности, полностью упорядоченные множества также можно называть «упорядоченными множествами», особенно в областях, где эти структуры более распространены, чем частично упорядоченные множества. Некоторые авторы используют другие символы, чем $\leq$ такой как $\sqsubseteq$ или $\preceq$ отличать частичные заказы от полных заказов.

Говоря о частичных заказах, $\leq$ не следует рассматривать как дополнение к $>$. Отношение $>$ является обратным иррефлексивному ядру $\leq$, которое всегда является подмножеством дополнения $\leq$, но $>$ равно дополнению $\leq$ тогда и только тогда, когда , $\leq$ это полный порядок.

Альтернативные определения

Другой способ определения частичного порядка, встречающийся в информатике , заключается в использовании понятия сравнения . В частности, учитывая $\leq ,<,\geq ,{\text{ and }}>$ как определено ранее, можно заметить, что два элемента и y могут находиться в любом из четырех взаимоисключающих отношений друг с другом: либо x < y , либо x = y , либо x > y , либо x и y несравнимы x . Это можно представить функцией ${\text{compare}}:P\times P\to \{<,>,=,\vert \}$ который возвращает один из четырех кодов при наличии двух элементов. Это определение эквивалентно частичному порядку на сетоиде , где равенство считается определенным отношением эквивалентности, а не равенством множеств.

Уоллис определяет более общее понятие отношения частичного порядка как любое однородное отношение , которое является транзитивным и антисимметричным . Сюда входят как рефлексивные, так и иррефлексивные частичные заказы как подтипы.

Конечное ЧУ-множество можно визуализировать через его диаграмму Хассе . В частности, взяв строгое отношение частичного порядка $(P,<)$ ( ориентированный ациклический граф DAG) можно построить, взяв каждый элемент $P$ быть узлом и каждым элементом $<$ быть краем. Транзитивная редукция этого DAG тогда это диаграмма Хассе. Аналогичным образом этот процесс можно обратить вспять, чтобы создать строгие частичные заказы из определенных групп DAG. Напротив, граф, связанный с нестрогим частичным порядком, имеет циклы в каждом узле и, следовательно, не является DAG; когда говорят, что нестрогий порядок изображается диаграммой Хассе, на самом деле показан соответствующий строгий порядок.

Примеры

Рис. 3 График делимости чисел от 1 до 4. Это множество частично, но не полностью упорядочено, поскольку существует связь от 1 с каждым другим числом, но нет связи от 2 к 3 или 3 к 4

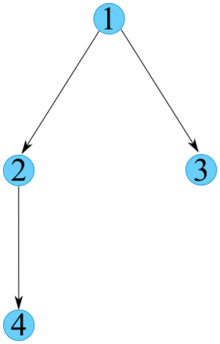
Стандартные примеры ЧУМ, возникающих в математике, включают:

• Действительные числа или вообще любой полностью упорядоченный набор, упорядоченный по стандартному отношению «меньше или равно» ≤, является частичным порядком.
• О реальных цифрах $\mathbb {R}$, обычное отношение меньше чем < является строгим частичным порядком. То же самое относится и к обычному отношению «больше чем » > на $\mathbb {R}$.
• По определению, каждый строгий слабый порядок является строгим частичным порядком.
• Множество подмножеств данного множества (его степенное множество ), упорядоченное по включению (см. рис. 1). Аналогично, набор последовательностей, упорядоченных по подпоследовательности , и набор строк, упорядоченных по подстроке .
• Множество натуральных чисел, снабженных отношением делимости . (см. рис. 3 и рис. 6)
• Множество вершин ориентированного ациклического графа, упорядоченное по достижимости .
• Множество подпространств векторного пространства, упорядоченное по включению.
• Для частично упорядоченного набора P — пространство последовательностей , содержащее все последовательности элементов из P , где последовательность a предшествует последовательности b, если каждый элемент в a предшествует соответствующему элементу в b . Формально, $\left(a_{n}\right)_{n\in \mathbb {N} }\leq \left(b_{n}\right)_{n\in \mathbb {N} }$ тогда и только тогда, когда $a_{n}\leq b_{n}$ для всех $n\in \mathbb {N}$; то есть покомпонентный порядок .
• Для набора X и частично упорядоченного набора P , функциональное пространство содержащее все функции от X до P , где f ≤ g тогда и только тогда, когда f ( x ) ≤ g ( x ) для всех $x\in X.$
• Забор — определяемый чередующейся последовательностью отношений порядка a <b> набор , ... c < d частично упорядоченный
• Набор событий в специальной теории относительности и, в большинстве случаев, Общая теория относительности где для двух событий X и Y , X ≤ Y только тогда, когда находится в будущем световом конусе X. Y тогда и На событие Y может причинно повлиять X только в том случае, если X ≤ Y .

Один знакомый пример частично упорядоченного множества — это совокупность людей, упорядоченных по генеалогическому происхождению. Некоторые пары людей имеют отношения потомок-предок, но другие пары людей несравнимы, поскольку ни один из них не является потомком другого.

Заказы на декартово произведение частично упорядоченных множеств

Рис. 4а Лексикографический порядок на $\mathbb {N} \times \mathbb {N}$

Рис. 4b Заказ продукта на $\mathbb {N} \times \mathbb {N}$

Рис. 4в Рефлексивное закрытие строгого прямого заказа на продукцию $\mathbb {N} \times \mathbb {N} .$ Элементы, ( покрытые 3, 3) и покрывающие (3, 3), выделены зеленым и красным цветом соответственно.

В порядке возрастания силы, т. е. убывания наборов пар, можно выделить три возможных частичных порядка декартова произведения двух частично упорядоченных наборов (см. рис. 4):

• лексикографический порядок : ( a , b ) ≤ ( c , d ), если a < c или ( a = c и b ≤ d );
• порядок продукта : ( a , b ) ≤ ( c , d ), если a ≤ c и b ≤ d ;
• рефлексивное замыкание прямого произведения соответствующих строгих порядков: ( a , b ) ≤ ( c , d ) , если ( a < c и b < d ) или ( a = c и b = d ).

Все три могут быть аналогичным образом определены для декартова произведения более двух множеств.

Применительно к упорядоченным векторным пространствам над одним и тем же полем результат в каждом случае также является упорядоченным векторным пространством.

См. также заказы на декартово произведение полностью упорядоченных множеств .

Суммы частично упорядоченных множеств

Другой способ объединить два (непересекающихся) частично упорядоченных множества — это порядковая сумма. (или линейная сумма ), Z = X ⊕ Y , определенный в объединении базовых множеств X и Y порядком a ⩽ _Z b тогда и только тогда, когда:

• a , b ∈ X с a ≤ _X b , или
• a , b ∈ Y с a ≤ _Y b , или
• а € X и б € Y .

Если два ЧУУ упорядочены , то упорядочена и их порядковая сумма.

Последовательно-параллельные частичные заказы формируются из операции порядковой суммы (в данном контексте называемой композицией серии) и другой операции, называемой параллельной композицией. Параллельная композиция — это непересекающееся объединение двух частично упорядоченных множеств без отношения порядка между элементами одного множества и элементами другого множества.

Производные понятия

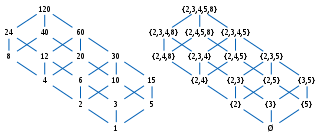
В примерах используется установочный набор $({\mathcal {P}}(\{x,y,z\}),\subseteq )$ состоящий из множества всех подмножеств трехэлементного множества $\{x,y,z\},$ упорядочены по включению множества (см. рис. 1).

• a относится к b, когда a ≤ b . Это не означает, что b также связано с a , поскольку отношение не обязательно должно быть симметричным . Например, $\{x\}$ связано с $\{x,y\},$ но не наоборот.
• a и b сравнимы , если a ≤ b или b ≤ a . В остальном они несравнимы . Например, $\{x\}$ и $\{x,y,z\}$ сопоставимы, в то время как $\{x\}$ и $\{y\}$ нет.
• Полный порядок или линейный порядок — это частичный порядок, при котором каждая пара элементов сравнима, т. е. трихотомия сохраняется . Например, натуральные числа со стандартным порядком.
• Цепочка — это подмножество частично упорядоченного множества. Например, $\{\{\,\},\{x\},\{x,y,z\}\}$ это цепь.
• Антицепь — это подмножество частичного множества, в котором нет двух различных элементов, сравнимых друг с другом. Например, набор синглтонов $\{\{x\},\{y\},\{z\}\}.$
• элемент a Говорят, что строго меньше элемента b , если a ≤ b и $a\neq b.$ Например, $\{x\}$ строго меньше, чем $\{x,y\}.$
• элемент a Говорят, что покрыт другим элементом b , записанным a ⋖ b (или a <: b ), если a строго меньше b не помещается третий элемент c и между ними ; формально: если оба a ≤ b и $a\neq b$ верны, а a ≤ c ≤ b ложно для каждого c с $a\neq c\neq b.$ Используя строгий порядок <, отношение a ⋖ b можно эквивалентно перефразировать как « a < b, но не a < c < b для любого c ». Например, $\{x\}$ покрыто $\{x,z\},$ но не покрывается $\{x,y,z\}.$

Экстрим

Рис. 5. Рисунок выше, из которого удалены наибольший и наименьший элементы. В этом уменьшенном частично упорядоченном наборе все элементы верхнего ряда представляют собой максимальные элементы, а все элементы нижнего ряда — минимальные , но нет ни наибольшего , ни наименьшего элемента.

В частичном наборе есть несколько понятий «наибольшего» и «наименьшего» элемента. $P,$ в частности:

• Величайший элемент и наименьший элемент: элемент $g\in P$ является величайшим элементом, если $a\leq g$ для каждого элемента $a\in P.$ Элемент $m\in P$ является наименьшим элементом, если $m\leq a$ для каждого элемента $a\in P.$ ЧУ-множество может иметь только один наибольший или наименьший элемент. В нашем примере набор $\{x,y,z\}$ является величайшим элементом, и $\{\,\}$ является наименьшим.
• Максимальные элементы и минимальные элементы: элемент $g\in P$ является максимальным элементом, если не существует элемента $a\in P$ такой, что $a>g.$ Аналогично, элемент $m\in P$ является минимальным элементом, если нет элемента $a\in P$ такой, что $a<m.$ Если ЧУ-множество имеет наибольший элемент, он должен быть уникальным максимальным элементом, но в противном случае может быть более одного максимального элемента, и аналогично для наименьших и минимальных элементов. В нашем рабочем примере $\{x,y,z\}$ и $\{\,\}$ — максимальный и минимальный элементы. Если убрать их, останется 3 максимальных элемента и 3 минимальных элемента (см. рис. 5).
• Верхняя и нижняя границы : для подмножества A из P элемент x в P является верхней границей A, a ≤ x , для каждого элемента a в A. если В частности, x не обязательно должен находиться в A, чтобы быть верхней границей A . Аналогично, элемент x в P является нижней границей A, a ≥ x , для каждого элемента a в A. если Наибольший элемент P — это верхняя граница самого P , а наименьший элемент — нижняя P. граница В нашем примере набор $\{x,y\}$ является верхней границей набора элементов $\{\{x\},\{y\}\}.$

Рис. 6. Неотрицательные целые числа , упорядоченные по делимости

В качестве другого примера рассмотрим положительные целые числа , упорядоченные по делимости: 1 — наименьший элемент, так как он делит все остальные элементы; с другой стороны, в этом частичном наборе нет наибольшего элемента. В этом частично упорядоченном множестве даже нет максимальных элементов, поскольку любой g делит, например, 2 g , отличный от него, поэтому g не является максимальным. Если исключить число 1, сохранив при этом делимость как порядок на элементы больше 1, то в результирующем ЧУМ нет наименьшего элемента, но любое простое число является для него минимальным элементом. В этом частичном наборе 60 является верхней границей (но не наименьшей верхней границей) подмножества. $\{2,3,5,10\},$ который не имеет нижней границы (поскольку 1 не входит в частично упорядоченное множество); с другой стороны, 2 — это нижняя граница подмножества степеней 2, которая не имеет верхней границы. Если включено число 0, это будет наибольший элемент, поскольку он кратен каждому целому числу (см. рис. 6).

Отображения между частично упорядоченными наборами

Рис. 7а Порядок сохраняющий, но не отражающий порядок (поскольку f ( u ) ≼ f ( v ) , а не u $\leq$ в) карта.

Рис. 7b Порядковый изоморфизм между делителями числа 120 (частично упорядоченными по делимости) и замкнутыми дивизорами подмножествами {2, 3, 4, 5, 8} (частично упорядоченными по включению множества)

Учитывая два частично упорядоченных набора ( S , ≤) и ( T , ≼) , функция $f:S\to T$ называется сохраняющим порядок , или монотонным , или изотонным , если для всех $x,y\in S,$ $x\leq y$ подразумевает ж ( Икс ) ≼ ж ( у ) .Если ( U , ≲) также является частично упорядоченным множеством, и оба $f:S\to T$ и $g:T\to U$ сохраняют порядок, их состав $g\circ f:S\to U$ также сохраняет порядок.Функция $f:S\to T$ называется отражающим порядок, если для всех $x,y\in S,$ ж ( Икс ) ≼ ж ( у ) подразумевает $x\leq y.$Если f одновременно сохраняет порядок и отражает порядок, то это называется вложением порядка ( S , ≤) в ( T , ≼) .В последнем случае f обязательно инъективен , поскольку $f(x)=f(y)$ подразумевает $x\leq y{\text{ and }}y\leq x$ и в свою очередь $x=y$ в соответствии с антисимметрией $\leq .$ Если существует порядковое вложение между двумя частично упорядоченными множествами S и T , говорят, что S можно вложить в T . Если вложение порядка $f:S\to T$ является биективным , его называют изоморфизмом порядка , а частичные порядки ( S , ≤) и ( T , ≼) называются изоморфными . Изоморфные порядки имеют структурно схожие диаграммы Хассе (см. рис. 7а). Можно показать, что если сохраняющие порядок отображения $f:S\to T$ и $g:T\to U$ существуют такие, что $g\circ f$ и $f\circ g$ дает тождественную функцию на S и T соответственно, тогда S и T порядково-изоморфны.

Например, отображение $f:\mathbb {N} \to \mathbb {P} (\mathbb {N} )$ от набора натуральных чисел (упорядоченных по делимости) к степенному набору натуральных чисел (упорядоченному по включению множества) можно определить, приведя каждое число к множеству его простых делителей . Это сохраняет порядок: если x делит y , то каждый простой делитель x также является простым делителем y . Однако он не является инъективным (поскольку он отображает и 12, и 6 в $\{2,3\}$) и не отражающий порядок (поскольку 12 не делит 6). Вместо этого приведение каждого числа к множеству его простых делителей определяет отображение $g:\mathbb {N} \to \mathbb {P} (\mathbb {N} )$ это сохранение порядка, отражение порядка и, следовательно, вложение порядка. Это не изоморфизм порядка (поскольку он, например, не отображает никакое число в множество $\{4\}$), но его можно сделать таковым, ограничив его кодомен до $g(\mathbb {N} ).$ На рис. 7b показано подмножество $\mathbb {N}$ и его изоморфный образ относительно g . Построение такого изоморфизма порядка в степенное множество можно обобщить на широкий класс частичных порядков, называемых дистрибутивными решетками ; см. теорему о представлении Биркгофа .

Количество частичных заказов

Последовательность A001035 в OEIS дает количество частичных заказов в наборе из n помеченных элементов:

Количество n -элементных бинарных отношений разных типов

Elem­ents	Любой	Переходный	Рефлексивный	Симметричный	Предварительный заказ	Частичный заказ	Общий предзаказ	Общий заказ	Отношение эквивалентности
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
н	2 н 2		2 п ( п -1)	2 п ( п +1)/2			∑ н к = 0 к ! С ( п , к )	н !	∑ н k =0 S ( n , k )
ОЭИС	А002416	А006905	А053763	А006125	А000798	А001035	А000670	А000142	А000110

Обратите внимание, что S ( n , k ) относится к числам Стирлинга второго рода .

Количество строгих частичных заказов такое же, как и у частичных заказов.

Если счет производится только до последовательность 1, 1, 2, 5, 16, 63, 318,... (последовательность A000112 в OEIS изоморфизма, то получается ).

Подмножества

Посет $P^{*}=(X^{*},\leq ^{*})$ называется подмножеством другого частичного множества $P=(X,\leq )$ при условии, что $X^{*}$ является подмножеством ​ $X$ и $\leq ^{*}$ является подмножеством $\leq$. Последнее условие эквивалентно требованию, чтобы для любого $x$ и $y$ в $X^{*}$ (и, следовательно, также в $X$), если $x\leq ^{*}y$ затем $x\leq y$.

Если $P^{*}$ является подмножеством $P$ и более того, для всех $x$ и $y$ в $X^{*}$, в любое время $x\leq y$ у нас также есть $x\leq ^{*}y$, то мы позвоним $P^{*}$ подмножество $P$ вызванный ​ $X^{*}$, и напиши $P^{*}=P[X^{*}]$.

Линейное расширение

Частичный заказ $\leq ^{*}$ на съемочной площадке $X$ называется расширением другого частичного порядка $\leq$ на $X$ при условии, что для всех элементов $x,y\in X,$ в любое время $x\leq y,$ это также тот случай, что $x\leq ^{*}y.$ Линейное расширение — это расширение, которое также является линейным (то есть полным) порядком. Классический пример: лексикографический порядок полностью упорядоченных множеств является линейным расширением порядка их произведений. Каждый частичный порядок может быть расширен до полного порядка ( принцип расширения порядка ).

В информатике алгоритмы поиска линейных расширений частичных порядков (представленных как достижимости порядки ориентированных ациклических графов ) называются топологической сортировкой .

В теории категорий

Основная статья: Посетальная категория

Каждый ЧУУ (и каждый предупорядоченный набор ) можно рассматривать как категорию , в которой для объектов $x$ и $y,$ существует не более одного морфизма из $x$ к $y.$ Более подробно, пусть hom( x , y ) = {( x , y )}, если x ≤ y (и в противном случае пустое множество ), и $(y,z)\circ (x,y)=(x,z).$ Такие категории иногда называют посетальными .

Частные множества эквивалентны друг другу тогда и только тогда, когда они изоморфны . В частичном наборе наименьший элемент, если он существует, является начальным объектом , а самый большой элемент, если он существует, является конечным объектом . Кроме того, каждый предварительно упорядоченный набор эквивалентен частичному множеству. Наконец, каждая подкатегория ЧУ множества изоморфно замкнута .

Частичные порядки в топологических пространствах

Основная статья: Частично упорядоченное пространство

Если $P$ — частично упорядоченное множество, которому также задана структура топологического пространства , то принято считать, что $\{(a,b):a\leq b\}$ является замкнутым подмножеством топологического пространства произведений $P\times P.$ При этом предположении отношения частичного порядка хорошо ведут себя на пределе в том смысле, что если $\lim _{i\to \infty }a_{i}=a,$ и $\lim _{i\to \infty }b_{i}=b,$ и для всех $i,$ $a_{i}\leq b_{i},$ затем $a\leq b.$

Интервалы

См. Также: Интервал (математика)

Выпуклое множество в частично упорядоченном множестве P — это подмножество I в P, обладающее тем свойством, что для любых и y в I и любого z в P , если x ⩽ z ⩽ y , то z также находится в I. x Это определение обобщает определение интервалов действительных чисел . Когда возможна путаница с выпуклыми множествами , геометрии используется порядково-выпуклый вместо слова «выпуклый» .

Выпуклая подрешетка решетки L L. — это подрешетка решетки L которая также является выпуклым множеством решетки , пересечение фильтра и идеала L Любую непустую выпуклую подрешетку можно однозначно представить как .

Интервал — это в частичном наборе P подмножество, которое можно определить с помощью обозначения интервала:

• Для a ≤ b [ замкнутый интервал a , b ] представляет собой набор элементов x, удовлетворяющих a ≤ x ≤ b (то есть a ≤ x и x ≤ b ). Он содержит как минимум элементы a и b .
• Используя соответствующее строгое отношение «<», открытый интервал ( a , b ) представляет собой набор элементов x, удовлетворяющих a < x < b (т. е. a < x и x < b ). Открытый интервал может быть пустым, даже если a < b . Например, открытый интервал (0, 1) для целых чисел пуст, поскольку не существует целого числа x такого, что 0 < x < 1 .
• Полуинтервалы [ b a , b ) и ( a , ] . определяются аналогично

Всякий раз, когда a ≤ b не выполняется, все эти интервалы пусты. Каждый интервал представляет собой выпуклое множество, но обратное неверно; например, в упорядоченном по делимости наборе делителей числа 120 (см. рис. 7б) множество {1, 2, 4, 5, 8} является выпуклым, но не интервалом.

Интервал I ограничен, если существуют элементы $a,b\in P$ такой, что я ⊆ [ а , б ] . Любой интервал, который можно представить в интервальных обозначениях, очевидно, ограничен, но обратное неверно. Например, пусть P = (0, 1) ∪ (1, 2) ∪ (2, 3) как подмножество действительных чисел. Подмножество (1, 2) представляет собой ограниченный интервал, но оно не имеет нижней или верхней границы в P , поэтому его нельзя записать в интервальной записи с использованием P. элементов

ЧУ-множество называется локально конечным, если каждый ограниченный интервал конечен. Например, целые числа локально конечны при их естественном порядке. Лексикографический порядок декартова произведения $\mathbb {N} \times \mathbb {N}$ не является локально конечным, поскольку (1, 2) ⩽ (1, 3) ⩽ (1, 4) ⩽ (1, 5) ⩽ ... ⩽ (2, 1) .Используя интервальную запись, свойство « a покрывается b » можно эквивалентно перефразировать как $[a,b]=\{a,b\}.$

Эту концепцию интервала в частичном порядке не следует путать с особым классом частичных порядков, известным как интервальные порядки .

См. также

• Антиматроид , формализация упорядочения на множестве, которая допускает более общие семейства порядков, чем частично упорядоченные множества.
• Причинное множество — подход к квантовой гравитации, основанный на частичном множестве.
• Граф сопоставимости - граф, связывающий пары сравнимых элементов в частичном порядке.
• Полный частичный порядок - термин, используемый в теории математического порядка. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Направленный набор – математический порядок с верхними границами.
• Градуированный частично упорядоченный набор - частично упорядоченный набор, оснащенный функцией ранга. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Алгебра инцидентности - ассоциативная алгебра, используемая в комбинаторике, разделе математики.
• Решетка - набор, пары которого имеют минимумы и максимумы.
• Локально конечное упорядоченное множество — страницы математики , отображающие описания викиданных в качестве запасного варианта. Страницы, отображающие краткие описания без пробелов.
• Функция Мёбиуса на частично упорядоченных множествах - ассоциативная алгебра, используемая в комбинаторике, разделе математики.
• Коллекция вложенных наборов
• Заказать многогранник
• Упорядоченное поле – алгебраический объект с упорядоченной структурой.
• Упорядоченная группа — группа с совместимым частичным порядком. Страницы, отображающие краткие описания целей перенаправления.
• Упорядоченное векторное пространство - векторное пространство с частичным порядком.
• Топология ЧУМ — своего рода топологическое пространство, которое можно определить из любого ЧУМ-множества.
• Непрерывность Скотта – непрерывность функции между двумя частичными порядками.
• Полурешетка - Частичный порядок с соединениями
• Полупорядок – числовой порядок с погрешностью.
• Теорема расширения Шпильрайна - каждый частичный порядок содержится в некотором полном порядке.
• Стохастическое доминирование - частичный порядок между случайными величинами.
• Строгий слабый порядок – строгий частичный порядок «<», при котором отношение «ни a < b , ни b < a » не является транзитивным.
• Общий порядок - заказ, все элементы которого сопоставимы.
• Лемма Цорна - математическое утверждение, эквивалентное аксиоме выбора.

Ссылки

• Дэйви, бакалавр; Пристли, ХА (2002). Введение в решетки и порядок (2-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-78451-1 .
• Дешпанде, Джаянт В. (1968). «О непрерывности частичного приказа» . Труды Американского математического общества . 19 (2): 383–386. дои : 10.1090/S0002-9939-1968-0236071-7 .
• Шмидт, Гюнтер (2010). Реляционная математика . Энциклопедия математики и ее приложений. Том. 132. Издательство Кембриджского университета. ISBN  978-0-521-76268-7 .
• Бернд Шредер (11 мая 2016 г.). Упорядоченные множества: введение в связи от комбинаторики к топологии . Биркхойзер. ISBN  978-3-319-29788-0 .
• Стэнли, Ричард П. (1997). Перечислительная комбинаторика 1 . Кембриджские исследования по высшей математике. Том. 49. Издательство Кембриджского университета. ISBN  0-521-66351-2 .
• Эйленберг, С. (2016). Основы алгебраической топологии . Издательство Принстонского университета.
• Кальмбах, Г. (1976). «Распространение теории гомологии на частично упорядоченные множества». Дж. Рейн Анжью. Математика . 280 : 134–156.

Внешние ссылки

• Последовательность OEIS A001035 (количество частично упорядоченных наборов с n помеченными элементами)
• Последовательность OEIS A000112 (Количество частично упорядоченных наборов («posesets») с n непомеченными элементами.)