Монотонная функция

«Монотонность» перенаправляется сюда. Информацию о монотонности применительно к системам голосования см. в разделе «Критерий монотонности» . Информацию о монотонности применительно к логическим системам см. в разделе « Монотонность следствия» .

«Монотонный» перенаправляется сюда. Чтобы узнать о других значениях, см. «Монотонность» (значения) .

Рис. 1. Монотонно неубывающая функция

Рис. 2. Монотонно невозрастающая функция

Рисунок 3. Функция, которая не является монотонной

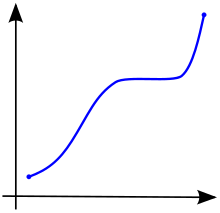
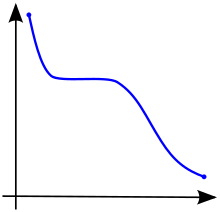
В математике ( монотонная функция или монотонная функция ) — это функция между упорядоченными множествами , которая сохраняет или меняет заданный порядок . Эта концепция впервые возникла в исчислении , а затем была обобщена до более абстрактной теории порядка .

В исчислении и анализе

В исчислении функция $f$ определенный на подмножестве действительных чисел с действительными значениями, называется монотонным, если он либо полностью не возрастает, либо полностью не убывает. То есть, согласно рис. 1, функция, монотонно возрастающая, не обязательно должна только возрастать, она просто не должна убывать.

Функция называется монотонно возрастающей (также возрастающей или неубывающей ). если для всех $x$ и $y$ такой, что $x\leq y$ у одного есть $f\!\left(x\right)\leq f\!\left(y\right)$, так $f$ сохраняет порядок (см. рисунок 1). Аналогично функция называется монотонно убывающей (также убывающей или невозрастающей ). если, когда угодно $x\leq y$, затем $f\!\left(x\right)\geq f\!\left(y\right)$, поэтому меняется на обратный порядок (см. рисунок 2).

Если заказ $\leq$ в определении монотонности заменяется строгим порядком $<$, получаем более сильное требование. Функция, обладающая этим свойством, называется строго возрастающей (также возрастающей ). Опять же, инвертируя символ порядка, можно найти соответствующее понятие, называемое строго убывающим (тоже убывающим ). Функция, обладающая любым из этих свойств, называется строго монотонной . Функции, которые являются строго монотонными, являются взаимно однозначными (поскольку для $x$ не равен $y$, или $x<y$ или $x>y$ и поэтому по монотонности либо $f\!\left(x\right)<f\!\left(y\right)$ или $f\!\left(x\right)>f\!\left(y\right)$, таким образом $f\!\left(x\right)\neq f\!\left(y\right)$.)

Чтобы избежать двусмысленности, термины «слабо монотонно» , «слабо возрастающее» и «слабо убывающее» часто используются для обозначения нестрогой монотонности.

Термины «неубывающий» и «невозрастающий» не следует путать с (гораздо более слабыми) отрицательными определениями «не убывающий» и «не возрастающий». Например, немонотонная функция, показанная на рисунке 3, сначала падает, затем возрастает, затем снова падает. Следовательно, оно не уменьшается и не увеличивается, но оно не является ни неубывающим, ни невозрастающим.

Функция $f$ называется абсолютно монотонным на интервале $\left(a,b\right)$ если производные всех порядков $f$ неотрицательны неположительны или во всех точках интервала.

Обратная функция

Все строго монотонные функции обратимы, поскольку они гарантированно имеют взаимно однозначное отображение своего диапазона в свою область определения.

Однако функции, которые являются лишь слабо монотонными, не являются обратимыми, поскольку они постоянны на некотором интервале (и, следовательно, не являются взаимно однозначными).

Функция может быть строго монотонной в ограниченном диапазоне значений и, следовательно, иметь обратную функцию в этом диапазоне, даже если она не является строго монотонной всюду. Например, если $y=g(x)$ строго возрастает в диапазоне $[a,b]$, то оно имеет обратное $x=h(y)$ на полигоне $[g(a),g(b)]$.

Термин «монотонный» иногда используется вместо «строго монотонный» , поэтому источник может утверждать, что все монотонные функции обратимы, хотя на самом деле это означает, что все строго монотонные функции обратимы.

Монотонное преобразование

Термин монотонное преобразование (или монотонное преобразование ) также может вызвать путаницу, поскольку он относится к преобразованию с помощью строго возрастающей функции. Так обстоит дело в экономике, когда порядковые свойства функции полезности сохраняются при монотонном преобразовании (см. Также монотонные предпочтения ). В этом контексте термин «монотонное преобразование» относится к положительному монотонному преобразованию и предназначен для того, чтобы отличить его от «отрицательного монотонного преобразования», которое меняет порядок чисел.

Некоторые основные приложения и результаты

Монотонная функция с плотным набором скачкообразных разрывов (показаны несколько участков)

Графики 6 функций монотонного роста

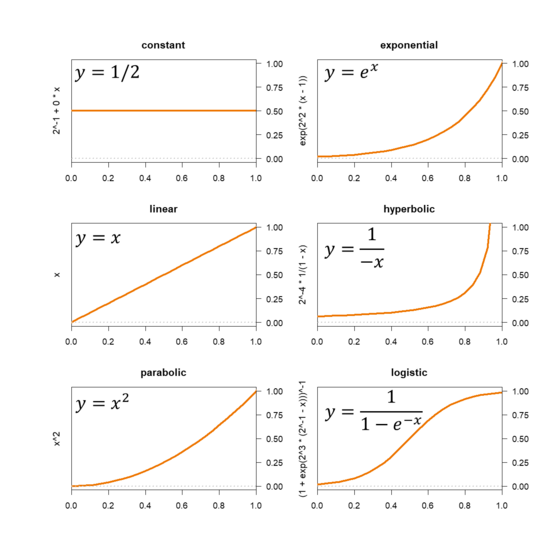
Следующие свойства справедливы для монотонной функции $f\colon \mathbb {R} \to \mathbb {R}$:

• $f$ имеет пределы справа и слева в каждой точке своей области ;
• $f$ имеет предел на положительной или отрицательной бесконечности ( $\pm \infty$) либо действительного числа, $\infty$, или $-\infty$.
• $f$ может иметь только скачкообразные разрывы ;
• $f$ может иметь только счетное число разрывов в своей области. Однако разрывы не обязательно состоят из изолированных точек и могут даже быть плотными на интервале ( a , b ). Например, для любой суммируемой последовательности $(a_{i})$ положительных чисел и любого перечисления $(q_{i})$ рациональных чисел монотонно возрастающая функция $$f(x)=\sum _{q_{i}\leq x}a_{i}$$ непрерывен ровно в каждом иррациональном числе (см. рисунок). Это кумулятивная функция распределения дискретной меры рациональных чисел, где $a_{i}$ это вес $q_{i}$.
• Если $f$ дифференцируема ​ в $x^{*}\in {\mathbb {R}}$ и $f'(x^{*})>0$, то существует невырожденный интервал I такой, что $x^{*}\in I$ и $f$ увеличивается I. на частичное обратное, если f дифференцируема и возрастает на интервале I , то ее производная положительна в каждой точке I. Как

Эти свойства являются причиной того, почему монотонные функции полезны в технической работе по анализу . Другие важные свойства этих функций включают в себя:

• если $f$ — монотонная функция, определенная на интервале $I$, затем $f$ дифференцируема на почти всюду $I$; то есть набор чисел $x$ в $I$ такой, что $f$ не дифференцируема в $x$ имеет Лебега нулевую меру . Кроме того, этот результат невозможно улучшить до счетного: см. функцию Кантора .
• если это множество счетно, то $f$ абсолютно непрерывен
• если $f$ — монотонная функция, определенная на интервале $\left[a,b\right]$, затем $f$ интегрируема по Риману .

Важным применением монотонных функций является теория вероятностей . Если $X$ — случайная величина , ее кумулятивная функция распределения $F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)$ является монотонно возрастающей функцией.

Функция называется унимодальной , если она монотонно возрастает до некоторой точки ( мода ), а затем монотонно убывает.

Когда $f$ является строго монотонной функцией, то $f$ инъективен в своей области определения , и если $T$ это диапазон ​ $f$, то существует обратная функция $T$ для $f$. Напротив, каждая постоянная функция монотонна, но не инъективна. и, следовательно, не может иметь обратного.

На графике показаны шесть монотонных функций. Их простейшие формы показаны в области графика, а выражения, использованные для их создания, показаны на Y. оси

В топологии

Карта $f:X\to Y$ называется монотонным если все его волокна связны , ; то есть для каждого элемента $y\in Y,$ набор (возможно, пустой) $f^{-1}(y)$ связным подпространством является $X.$

В функциональном анализе

В функциональном анализе топологического векторного пространства $X$, (возможно, нелинейный) оператор $T:X\rightarrow X^{*}$ называется монотонным оператором, если

$$(Tu-Tv,u-v)\geq 0\quad \forall u,v\in X.$$Теорема Качуровского показывает, что выпуклые функции в банаховых пространствах имеют в качестве производных монотонные операторы.

Подмножество $G$ из $X\times X^{*}$ называется монотонным множеством, если для каждой пары $[u_{1},w_{1}]$ и $[u_{2},w_{2}]$ в $G$,

$$(w_{1}-w_{2},u_{1}-u_{2})\geq 0.$$$G$ называется максимальным монотонным, если оно максимально среди всех монотонных множеств в смысле включения множества. График монотонного оператора $G(T)$ представляет собой монотонное множество. Монотонный оператор называется максимальным монотонным , если его график представляет собой максимальное монотонное множество .

В порядке теории

Теория порядка рассматривает произвольные частично упорядоченные множества и предупорядоченные множества как обобщение действительных чисел. Приведенное выше определение монотонности актуально и в этих случаях. Однако терминов «возрастание» и «уменьшение» избегают, поскольку их обычное графическое представление не применимо к порядкам, которые не являются тотальными . Кроме того, строгие отношения $<$ и $>$ во многих нетотальных порядках малопригодны, и поэтому для них не вводится дополнительная терминология.

Сдача в аренду $\leq$ обозначают отношение частичного порядка любого частично упорядоченного множества, монотонную функцию, также называемую изотоном , или сохраняющий порядок , удовлетворяющий свойству

$$x\leq y\implies f(x)\leq f(y)$$

для всех x и y в своей области. Композиция двух монотонных отображений также монотонна.

Двойственное или понятие часто называют антитоном , антимонотонностью . порядка изменением Следовательно, функция антитона f удовлетворяет свойству

$$x\leq y\implies f(y)\leq f(x),$$

для всех x и y в своей области.

Постоянная функция бывает одновременно монотонной и антитонной; и наоборот, если f одновременно монотонна и антитонна и если область определения f представляет собой решетку , то f должно быть постоянным.

Монотонные функции занимают центральное место в теории порядка. Они появляются в большинстве статей на эту тему и в этих местах встречаются примеры из специальных приложений. Некоторые известные специальные монотонные функции представляют собой вложения порядка (функции, для которых $x\leq y$ тогда и только тогда, когда $f(x)\leq f(y))$ и изоморфизмы порядка ( сюръективные вложения порядка).

В контексте поисковых алгоритмов

В контексте поисковых алгоритмов монотонность (также называемая согласованностью) — это условие, применяемое к эвристическим функциям . Эвристика $h(n)$ является монотонным, если для каждого узла n и каждого преемника n' из n, сгенерированного любым действием a , предполагаемая стоимость достижения цели из n не превышает стоимость шага достижения n' плюс расчетная стоимость достижения цели от н' ,

$$h(n)\leq c\left(n,a,n'\right)+h\left(n'\right).$$

Это форма неравенства треугольника с n , n' и целью Gn _, ближайшей к n . Поскольку любая монотонная эвристика также допустима , монотонность является более строгим требованием, чем допустимость. Некоторые эвристические алгоритмы , такие как A*, могут оказаться оптимальными при условии, что используемая ими эвристика монотонна.

В логических функциях

С немонотонной функцией «если а, то и b , и с », ложные узлы появляются выше истинные узлы.

Диаграмма Хассе монотонной функции «соблюдаются хотя бы два из a , b , c ». Цвета обозначают выходные значения функции.

В булевой алгебре монотонной функцией называется такая, что для всех a _i и b _i в {0,1} , если a ₁ ⩽ b ₁ , a ₂ ⩽ b ₂ , ..., a _n ⩽ b _n (т. е. Декартово произведение {0, 1} ^н упорядочен по координатам ), то f( a ₁ , ..., a _n ) ≤ f( b ₁ , ... bn _, ) . Другими словами, булева функция является монотонной, если для каждой комбинации входных данных переключение одного из входных данных с ложного на истинное может привести только к переключению вывода с ложного на истинное, а не с истинного на ложное. Графически это означает, что n -арная булева функция является монотонной, когда ее представление в виде n -куба, помеченного значениями истинности, не имеет восходящего края от true до false . (Эта помеченная диаграмма Хассе является двойственной функции помеченной диаграмме Венна , которая является более распространенным представлением для n ≤ 3. )

Монотонные логические функции — это именно те, которые можно определить с помощью выражения, объединяющего входные данные (которое может появляться более одного раза), используя только операторы и и или (в частности, не запрещено). Например, «соблюдаются по крайней мере два из a , b , c » — это монотонная функция от a , b , c , поскольку ее можно записать, например, как (( a и b ) или ( a и c ) или ( b и c )).

Число таких функций от n переменных известно как Дедекинда число n .

Решение SAT , как правило, NP-сложная задача, может быть эффективно достигнуто, когда все задействованные функции и предикаты являются монотонными и логическими.

См. также

• Монотонная кубическая интерполяция
• Псевдомонотонный оператор
• Коэффициент ранговой корреляции Спирмена - мера монотонности набора данных.
• Полная монотонность
• Циклическая монотонность
• Операторная монотонная функция
• Функция монотонного набора
• Абсолютно и вполне монотонные функции и последовательности.

Библиография

• Бартл, Роберт Г. (1976). Элементы реального анализа (второе изд.).
• Гретцер, Джордж (1971). Теория решеток: первые понятия и дистрибутивные решетки . ISBN  0-7167-0442-0 .
• Пембертон, Малькольм; Рау, Николас (2001). Математика для экономистов: Вводный учебник . Издательство Манчестерского университета. ISBN  0-7190-3341-1 .
• Ренарди, Майкл и Роджерс, Роберт С. (2004). Введение в уравнения в частных производных . Тексты по прикладной математике 13 (Второе изд.). Нью-Йорк: Springer-Verlag. п. 356. ИСБН  0-387-00444-0 .
• Рисс, Фридьес и Бела Секефальви-Надь (1990). Функциональный анализ . Публикации Courier Dover. ISBN  978-0-486-66289-3 .
• Рассел, Стюарт Дж.; Норвиг, Питер (2010). Искусственный интеллект: современный подход (3-е изд.). Река Аппер-Сэддл, Нью-Джерси: Прентис-Холл. ISBN  978-0-13-604259-4 .
• Саймон, Карл П.; Блюм, Лоуренс (апрель 1994 г.). Математика для экономистов (первое изд.). ISBN  978-0-393-95733-4 . (Определение 9.31)

Внешние ссылки

• «Монотонная функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Сходимость монотонной последовательности Аник Дебнат и Томас Роксло (Школа Харкера), Демонстрационный проект Wolfram .
• Вайсштейн, Эрик В. «Монотонная функция» . Математический мир .