Самоподобие


В математике объект самоподобный точно или приблизительно похож на часть самого себя (т.е. целое имеет такую же форму, что и одна или несколько частей). Многие объекты в реальном мире, такие как береговые линии , являются статистически самоподобными: части из них показывают одинаковые статистические свойства во многих масштабах. [ 2 ] Самоподобность является типичным свойством фракталов . Масштабная инвариантность является точной формой самоподобия, где при любом увеличении есть меньший кусок объекта, который похож на целое. Например, сторона снежинки Кох является как симметричной , так и масштабной инвариантной; Это может быть постоянно увеличивать 3X без изменения формы. Нетривиальное сходство, очевидное в фракталах, отличается их тонкой структурой или деталями на произвольно небольших масштабах. В качестве контрпример , тогда как любая часть прямой линии может напоминать целое, дополнительная деталь не раскрывается.
Говорят, что развитие явления развития, демонстрируемого самоподобием, если числовое значение определенной наблюдаемой величины измеряются в разное время, отличаются, но соответствующее бессмысленное количество при заданном значении оставаться инвариантными. Это происходит, если количество демонстрирует динамическое масштабирование . Идея - это просто расширение идеи сходства двух треугольников. [ 3 ] [ 4 ] [ 5 ] Обратите внимание, что два треугольника похожи, если числовые значения их бок отличаются, однако соответствующие безразмерные величины, такие как их углы, совпадают.
Peitgen et al. Объясните концепцию как таковую:
Если части фигуры являются небольшими копиями целого, то фигура называется самоподобной .... Фигура строго самоподобна , если фигура может быть разложена на части, которые являются точными копиями целого. Любая произвольная часть содержит точную копию всей фигуры. [ 6 ]
Поскольку математически фрактал может демонстрировать самоподобность при неопределенном увеличении, невозможно воссоздать это физически. Peitgen et al. Предложите изучить самоподобие с использованием приближений:
Чтобы придать операционное значение для собственности самоподобия, мы обязательно ограничены в работе с конечными приближениями предельной фигуры. Это делается с использованием метода, который мы будем называть ящик для самоподобия, где измерения проводятся на конечных стадиях фигуры, используя сетки различных размеров. [ 7 ]
Этот словарный запас был представлен Бенотом Мандельбротом в 1964 году. [ 8 ]
Самоубийство
[ редактировать ]
В математике , самосовершенствование является особенностью фрактала части которых масштабируются различными количествами в направлениях X- и Y. Это означает, что для того, чтобы оценить самоопределение этих фрактальных объектов, их необходимо пересечь с помощью анизотропной аффинной трансформации .
Определение
[ редактировать ]Компактное конечный топологическое пространство x является самоподобным, если существует набор , индексируя набор неруктивных гомеоморфизмов для которого
Если , мы называем x SelfImaler, если это единственное непустое подмножество Y , так что приведенное выше уравнение соответствует Полем Мы называем
структура самоподобная . Гомеоморфизмы могут быть итерацией , что приведет к итерационной функциональной системе . Состав функций создает алгебраическую структуру моноида . Когда набор S имеет только два элемента, моноид известен как диадический моноид . Дьядический моноид может быть визуализирован как бесконечное бинарное дерево ; В более общем плане, если у набора есть элементы P , то моноид может быть представлен как P-Adic Tree.
Автоморфизмы ; диадического моноида являются группой модульной Автоморфизмы могут быть изображены как гиперболические вращения бинарного дерева.
Более общее представление, чем самоподобность-это самоубинство .
Примеры
[ редактировать ]

Набор Мандельброта также является самоподобным вокруг точек Misiurewicz .
Самоподобность имеет важные последствия для разработки компьютерных сетей, поскольку типичный сетевой трафик обладает самоподобными свойствами. Например, в Тетраффической Инженерной Инженерии шаблоны трафика с переключенными пакетами, по-видимому, статистически являются самоподобными. [ 9 ] Это свойство означает, что простые модели, использующие распределение Пуассона, являются неточными, и сети, разработанные без учета самоподобия, вероятно, будут функционировать неожиданным образом.
Аналогичным образом, движения фондового рынка описываются как демонстрация самоффинтности , то есть они кажутся самоподобными при преобразовании с помощью соответствующего аффинного преобразования для уровня показанных деталей. [ 10 ] Эндрю Ло описывает самоподобность журнала фондового рынка в эконометрике . [ 11 ]
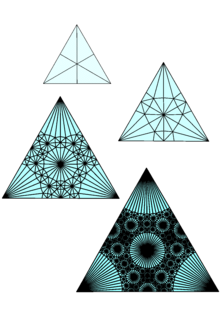
Конечные правила подразделения являются мощной техникой для создания самоподобных наборов, включая набор Cantor и треугольник Sierpinski .
В кибернетике
[ редактировать ]Жизненная система модели системы стаффорда - это организационная модель с аффинной самоподобной иерархией, где данная жизнеспособная система является одним из элементов системы, одной из жизнеспособной системы, один рекурсивный уровень, и для которого элементы его системы One жизнеспособные системы один рекурсивный уровень ниже.
В природе
[ редактировать ]
Самоподобность можно найти и в природе. Справа-это математически сгенерированное, совершенно самоподобное изображение папоротника , которое имеет заметное сходство с природными папоротниками. Другие растения, такие как Romanesco Broccoli , демонстрируют сильную самопоклонность.
В музыке
[ редактировать ]- Строгие каноны отображают различные типы и количества самоподобия, как и разделы фуг .
- Тон Шепарда является самопознанием по частоте или досям длины волны.
- Датский названную композитор в соответствии с Nørgård использовал самоподобную целочисленную последовательность, «Infinity Series» в большей части своей музыки.
- В области поиска музыкальной информации о поиске музыкальной информации самоподобность обычно относится к тому факту, что музыка часто состоит из частей, которые повторяются во времени. [ 12 ] Другими словами, музыка самоподобна при временном переводе, а не (или в дополнение к) при масштабировании. [ 13 ]
Смотрите также
[ редактировать ]Ссылки
[ редактировать ]- ^ Мандельброт, Бенуа Б. (1982). Фрактальная геометрия природы , с.44. ISBN 978-0716711865 .
- ^ Мандельброт, Бенуа Б. (5 мая 1967 г.). «Как долго длится побережье Британии? Статистический самоподобие и дробное измерение» . Наука . Новая серия. 156 (3775): 636–638. Bibcode : 1967sci ... 156..636M . doi : 10.1126/science.156.3775.636 . PMID 17837158 . S2CID 15662830 . Архивировано из оригинала 19 октября 2021 года . Получено 12 ноября 2020 года . PDF
- ^ Хасан М.К., Хасан М.З., Павел Н.И. (2011). «Динамическое масштабирование, CollapsEand самоподобия в сети Барабаси-Альберта». J. Phys A: Математика. Теор . 44 (17): 175101. Arxiv : 1101.4730 . Bibcode : 2011jpha ... 44q5101k . doi : 10.1088/1751-8113/44/17/175101 . S2CID 15700641 .
{{cite journal}}: Cs1 maint: несколько имен: список авторов ( ссылка ) - ^ Hassan Mk, Hassan MZ (2009). «Появление фрактального поведения в конденсационной агрегации». Физический Преподобный 79 (2): 021406. Arxiv : 0901.2761 . Bibcode : 2009frve..79b1406h . doi : 10.1103/physreve.79.021406 . PMID 19391746 . S2CID 26023004 .
- ^ Dayeeen Fr, Hassan Mk (2016). «Мульти-мультифракальность, динамическое масштабирование и статистика соседства в взвешенной плоской стохастической решетке». Хаос, солитоны и фракталы . 91 : 228. Arxiv : 1409.7928 . Bibcode : 2016csf .... 91..228d . doi : 10.1016/j.chaos.2016.06.006 .
- ^ Пейтген, Хайнц-Отто; Юргенс, Хартмут; Saupe, Dietmar; Малецкий, Эван; Персиант, Терри; и Yunker, Lee (1991). Фракталы для классной комнаты: стратегическая деятельность первая , с.21. Springer-Verlag, Нью-Йорк. ISBN 0-387-97346-X и ISBN 3-540-97346-X .
- ^ Puges, et al (1991), с.22-3.
- ^ Как я обнаружил фракталы, интервью с Бенотом Мандельбротом , исследованием https://www.larecherche.fr/math%C3%A9matiques-histoire-desciences/%C2%AB-Comment-d%C3%A9Couvert -les-fractales-%c2%bb
- ^ Леланд, мы; Taqqu, MS; и др. (Январь 1995). «О самоподобном характере трафика Ethernet (расширенная версия)» (PDF) . Транзакции IEEE/ACM в сетях . 2 (1): 1–15. doi : 10.1109/90.282603 . S2CID 6011907 .
- ^ Бенуа Мандельброта (февраль 1999 г.). «Как фракталы могут объяснить, что не так с Уолл -стрит» . Scientific American .
- ^ Кэмпбелл, Ло и Макинлей (1991) « Эконометрика финансовых рынков», издательство Принстонского университета! ISBN 978-0691043012
- ^ Фут, Джонатан (30 октября 1999 г.). «Визуализация музыки и аудио с использованием самоподобия». Материалы Седьмой Международной конференции ACM по мультимедиа (часть 1) (PDF) . С. 77–80. Citeseerx 10.1.1.223.194 . doi : 10.1145/319463.319472 . ISBN 978-1581131512 Полем S2CID 3329298 . Архивировано (PDF) из оригинала 9 августа 2017 года.
- ^ Pareyon, Габриэль (апрель 2011 г.). О музыкальном самоподобию: межсемоз как синекдоша и аналогия (PDF) . Международный институт семиотики в Иматре; Семиотическое общество Финляндии. п. 240. ISBN 978-952-5431-32-2 Полем Архивировано из оригинала (PDF) 8 февраля 2017 года . Получено 30 июля 2018 года . (Также см. Google Books )
Внешние ссылки
[ редактировать ]- "Copperplate Chevrons" -самоободник фрактального масштабирования
- «Самоподобность» -новые статьи о самопоклонности. Алгоритм вальса
Самоубийство
[ редактировать ]- Мандельброт, Бенуа Б. (1985). «Самофактность и фрактальное измерение» (PDF) . Physica Scripta . 32 (4): 257–260. Bibcode : 1985 Phys ... 32..257M . doi : 10.1088/0031-8949/32/4/001 . S2CID 250815596 .
- Сапошников, Виктор; Foufoula-Georgiou, EFI (май 1996 г.). «Самоаффинность в плетеных реках» (PDF) . Исследование водных ресурсов . 32 (5): 1429–1439. Bibcode : 1996wrr .... 32.1429s . doi : 10.1029/96WR00490 . Архивировано (PDF) из оригинала 30 июля 2018 года . Получено 30 июля 2018 года .
- Бенуа Б. Мандельброт (2002). Гауссовая самоубинство и фракталы: глобальность, Земля, 1/F Шум и R/S . Спрингер. ISBN 978-0387989938 .





