Ошибка наблюдения

«Систематическая предвзятость» перенаправляется сюда. О социологическом и организационном явлении см. Системная предвзятость .

Ошибка наблюдения (или ошибка измерения ) — это разница между измеренным значением величины и ее неизвестным истинным значением . Такие ошибки присущи процессу измерения; например, длина, измеренная с помощью линейки, калиброванной в целых сантиметрах, будет иметь погрешность измерения в несколько миллиметров. Погрешность или неопределенность измерения можно оценить и указать для измерения, например, как 32,3 ± 0,5 см. (Ошибка или неточность в процессе измерения приведет к неправильному значению, а не к известной погрешности измерения.)

Ошибки измерения можно разделить на две составляющие: случайную и систематическую . Случайные ошибки — это ошибки в измерении, которые приводят к несогласованности измеримых значений при повторных измерениях постоянного атрибута или величины . Систематические ошибки — это ошибки, которые не определяются случайно, а вносятся повторяемыми процессами, присущими системе . относиться к ошибке с ненулевым средним значением , эффект которой не уменьшается при наблюдений усреднении Систематическая ошибка может также . Например, измерения длины линейкой, точно калиброванной в целых сантиметрах, будут подвержены случайной ошибке; неправильно откалиброванная линейка также будет давать систематическую ошибку.

Ошибки измерения можно суммировать с точки зрения точности и прецизионности .Погрешность измерения не следует путать с неопределенностью измерения .

Наука и эксперименты

Когда случайность или неопределенность, смоделированные теорией вероятностей таким ошибкам приписывается , они являются «ошибками» в том смысле, в котором этот термин используется в статистике ; увидеть ошибки и остатки в статистике .

Каждый раз, когда измерение повторяется, получаются немного разные результаты. Обычно используемая статистическая модель состоит в том, что ошибка состоит из двух аддитивных частей:

1. Систематическая ошибка , которая всегда возникает с одним и тем же значением, когда мы используем инструмент одним и тем же способом и в одном и том же случае.
2. Случайная ошибка , которая может варьироваться от наблюдения к другому.

Систематическую ошибку иногда называют статистической погрешностью . Его часто можно уменьшить с помощью стандартизированных процедур. Частью процесса обучения в различных науках является обучение тому, как использовать стандартные инструменты и протоколы, чтобы минимизировать систематическую ошибку.

Распределение измерений известного истинного значения как с постоянной систематической ошибкой, так и с нормально распределенной случайной ошибкой.

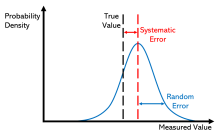
Случайная ошибка (или случайная вариация ) возникает из-за факторов, которые невозможно или невозможно контролировать. Одна из возможных причин отказаться от контроля этих случайных ошибок заключается в том, что контролировать их каждый раз, когда проводится эксперимент или проводятся измерения, может быть слишком дорого. Другие причины могут заключаться в том, что все, что мы пытаемся измерить, меняется во времени (см. Динамические модели ) или является фундаментально вероятностным (как в случае с квантовой механикой — см. Измерение в квантовой механике ). Случайная ошибка часто возникает, когда приборы доводятся до крайних пределов своих рабочих пределов. Например, цифровые весы часто демонстрируют случайную ошибку в младшей цифре. Три измерения одного объекта могут давать примерно такие значения: 0,9111 г, 0,9110 г и 0,9112 г.

Характеристика

Ошибки измерения можно разделить на две составляющие: случайную ошибку и систематическую ошибку.

Случайная ошибка всегда присутствует в измерении. Оно вызвано непредсказуемыми по своей сути колебаниями показаний измерительной аппаратуры или интерпретации экспериментатором показаний прибора. Случайные ошибки проявляются в виде разных результатов для якобы одного и того же повторного измерения. Их можно оценить путем сравнения нескольких измерений и уменьшить путем усреднения нескольких измерений.

Систематическая ошибка предсказуема и обычно постоянна или пропорциональна истинному значению. Если причину систематической ошибки можно определить, то ее обычно можно устранить. Систематические ошибки вызваны несовершенной калибровкой измерительных приборов или несовершенными методами наблюдения или вмешательством окружающей среды в процесс измерения и всегда влияют на результаты эксперимента в предсказуемом направлении. Неправильная установка нуля прибора является примером систематической ошибки приборов.

Стандарт испытаний производительности PTC 19.1-2005 «Неопределенность испытаний», опубликованный Американским обществом инженеров-механиков (ASME), подробно описывает систематические и случайные ошибки. Фактически, в этих терминах он концептуализирует свои основные категории неопределенности.

Случайная ошибка может быть вызвана непредсказуемыми колебаниями показаний измерительной аппаратуры или интерпретации экспериментатором показаний прибора; эти колебания могут быть частично обусловлены вмешательством окружающей среды в процесс измерения. Понятие случайной ошибки тесно связано с понятием точности . Чем выше точность измерительного прибора, тем меньше изменчивость ( стандартное отклонение ) колебаний его показаний.

Источники

Источники систематической ошибки

Неидеальная калибровка

Источниками систематической ошибки могут быть несовершенная калибровка средств измерений (нулевая ошибка), изменения в окружающей среде , которые мешают процессу измерения, а иногда и несовершенные методы наблюдения могут быть либо нулевой ошибкой, либо процентной ошибкой. Если вы представите экспериментатора, считывающего период времени, когда маятник проходит мимо контрольного маркера : если его секундомер или таймер запускается с 1 секундой на часах, то все его результаты будут отличаться на 1 секунду (нулевая ошибка). . возникнет процентная ошибка Если экспериментатор повторит этот эксперимент двадцать раз (каждый раз начиная с 1 секунды), то в вычислении среднего значения его результатов ; конечный результат будет немного больше истинного периода.

Расстояние , измеренное радаром, будет систематически завышаться, если не учитывать небольшое замедление волн в воздухе. Неправильная установка нуля прибора является примером систематической ошибки приборов.

Систематические ошибки могут также присутствовать в результатах оценки, основанной на математической модели или физическом законе . Например, расчетная частота колебаний маятника будет систематически ошибочной , если не учитывать небольшое движение опоры.

Количество

Систематические погрешности могут быть как постоянными, так и связанными (например, пропорциональными или процентными) с фактическим значением измеряемой величины или даже со значением другой величины (на показания линейки может влиять температура окружающей среды). Когда оно постоянное, то это происходит просто из-за неправильной обнуления прибора. Когда оно не является постоянным, оно может менять свой знак. Например, если на термометр влияет пропорциональная систематическая ошибка, равная 2% от фактической температуры, а фактическая температура составляет 200°, 0° или -100°, измеренная температура будет 204° (систематическая погрешность = + 4°), 0° (нулевая систематическая ошибка) или −102° (систематическая ошибка = −2°) соответственно. Таким образом, температура будет завышена, когда она будет выше нуля, и занижена, когда она будет ниже нуля.

Дрифт

Систематические ошибки, которые изменяются в ходе эксперимента ( дрейф ), легче обнаружить. Измерения указывают на тенденции во времени, а не на случайное изменение среднего значения . Дрейф очевиден, если измерение постоянной величины повторяется несколько раз и в течение эксперимента измерения смещаются в одну сторону. Если следующее измерение выше предыдущего измерения, что может произойти, если прибор нагревается во время эксперимента, тогда измеряемая величина является переменной, и можно обнаружить дрейф, проверяя нулевое показание во время эксперимента, а также в начале эксперимента. эксперимента (действительно, нулевое показание является измерением постоянной величины). Если нулевое показание постоянно выше или ниже нуля, имеется систематическая ошибка. Если это невозможно устранить, возможно, путем перезагрузки прибора непосредственно перед экспериментом, то это необходимо разрешить, вычитая его значение (возможно, изменяющееся во времени) из показаний и принимая его во внимание при оценке точности измерения.

Если закономерность в серии повторных измерений не очевидна, наличие фиксированных систематических ошибок можно обнаружить только при проверке измерений либо путем измерения известной величины, либо путем сравнения показаний с показаниями, полученными с использованием другого прибора, заведомо точнее. Например, если вы несколько раз задумаетесь о времени маятника с помощью точного секундомера, вы получите показания, случайно распределенные относительно среднего значения. Систематическая ошибка надежды имеет место, если секундомер сверяется с « говорящими часами » телефонной системы и обнаруживается, что он работает медленно или быстро. Очевидно, что время маятника необходимо корректировать в зависимости от того, насколько быстро или медленно работает секундомер.

Измерительные приборы, такие как амперметры и вольтметры, необходимо периодически проверять на соответствие известным стандартам.

Систематические ошибки также можно обнаружить путем измерения уже известных величин. Например, спектрометр, оснащенный дифракционной решеткой, можно проверить, используя его для измерения длины волны D-линий натрия электромагнитного спектра , которые составляют 600 нм и 589,6 нм. Измерения можно использовать для определения количества линий на миллиметр дифракционной решетки, что затем можно использовать для измерения длины волны любой другой спектральной линии.

С постоянными систематическими ошибками очень трудно бороться, поскольку их последствия можно наблюдать только в том случае, если их можно устранить. Такие ошибки невозможно устранить повторением измерений или усреднением большого количества результатов. Распространенным методом устранения систематической ошибки является калибровка измерительного прибора.

Источники случайных ошибок

Случайная или стохастическая ошибка измерения — это ошибка, которая случайна от одного измерения к другому. Стохастические ошибки имеют тенденцию к нормальному распределению , когда стохастическая ошибка представляет собой сумму многих независимых случайных ошибок из-за центральной предельной теоремы . объясняют изменение Y , которое не может быть объяснено включенными X. Стохастические ошибки, добавленные в уравнение регрессии ,

Опросы

Термин «ошибка наблюдения» также иногда используется для обозначения ошибок ответа и некоторых других типов ошибок, не связанных с выборкой . В ситуациях типа опроса этими ошибками могут быть ошибки при сборе данных, включая как неправильную запись ответа, так и правильную запись неточного ответа респондента. Эти источники ошибок, не связанных с выборкой, обсуждаются в Salant and Dillman (1994) и Bland and Altman (1996).

Эти ошибки могут быть случайными или систематическими. Случайные ошибки вызваны непреднамеренными ошибками респондентов, интервьюеров и/или кодировщиков. Систематическая ошибка может возникнуть в случае систематической реакции респондентов на метод, используемый для формулировки вопроса опроса. Таким образом, точная формулировка вопроса опроса имеет решающее значение, поскольку она влияет на уровень ошибки измерения. Исследователям доступны различные инструменты, которые помогут им принять решение о точной формулировке своих вопросов, например, оценка качества вопроса с помощью экспериментов MTMM . Эту информацию о качестве можно также использовать для исправления ошибок измерения .

Влияние на регрессионный анализ

Если зависимая переменная в регрессии измерена с ошибкой, регрессионный анализ и связанная с ним проверка гипотез не затрагиваются, за исключением того, что R ² будет ниже, чем при идеальном измерении.

Однако если одна или несколько независимых переменных измерены с ошибкой, то коэффициенты регрессии и стандартные проверки гипотез недействительны. Это известно как смещение затухания .

См. также

• Смещение (статистика)
• Когнитивная предвзятость
• Поправка на ошибку измерения (для корреляций Пирсона)
• Ошибки и остатки в статистике
• Ошибка
• Репликация (статистика)
• Статистическая теория
• Метрология
• Разбавление регрессии
• Метод испытания
• Распространение неопределенности
• Ошибка прибора
• Неопределенность измерения
• Модели ошибок в переменных
• Системная предвзятость

Дальнейшее чтение

• Кокран, WG (1968). «Ошибки измерения в статистике». Технометрика . 10 (4): 637–666. дои : 10.2307/1267450 . JSTOR   1267450 . S2CID   120645541 .