Гомология (математика)
В математике гомологии [а] — это общий способ связи последовательности алгебраических объектов, таких как абелевы группы или модули , с другими математическими объектами, такими как топологические пространства . Группы гомологии первоначально были определены в алгебраической топологии . Подобные конструкции доступны в самых разных других контекстах, таких как абстрактная алгебра , группы , алгебры Ли , теория Галуа и алгебраическая геометрия .
Первоначальной мотивацией для определения групп гомологии было наблюдение о том, что две формы можно различить, исследуя их отверстия. Например, круг не является диском, потому что в круге есть отверстие, в то время как диск твердый, а обычная сфера не является кругом, потому что сфера заключает в себе двумерное отверстие, а круг заключает в себе одномерное отверстие. Однако, поскольку дыры «нет», не сразу понятно, как ее определить или как различать разные виды дыр. Гомология изначально была строгим математическим методом определения и классификации дыр в многообразии . Грубо говоря, цикл — это замкнутое подмногообразие, граница — это цикл, который также является границей подмногообразия, а класс гомологий (который представляет дырку) — это класс эквивалентности циклов по модулю границ. Таким образом, класс гомологии представлен циклом, который не является границей какого-либо подмногообразия: цикл представляет собой дыру, а именно гипотетическое многообразие, границей которого был бы этот цикл, но которого «там нет».
Существует множество различных теорий гомологии. Определенный тип математического объекта, такой как топологическое пространство или группа , может иметь одну или несколько связанных теорий гомологии. Когда базовый объект имеет геометрическую интерпретацию, как это делают топологические пространства, n- я группа гомологии представляет поведение в измерении n . Большинство групп или модулей гомологии могут быть сформулированы как производные функторы на соответствующих абелевых категориях измеряя неспособность функтора , точно . С этой абстрактной точки зрения группы гомологии определяются объектами производной категории .
Предыстория [ править ]
Происхождение [ править ]
Можно сказать, что теория гомологии начинается с формулы многогранника Эйлера или характеристики Эйлера . [1] За этим последовало числовых определение Риманом инвариантов рода и n -кратной связности в 1857 году и доказательство Бетти в 1871 году независимости «чисел гомологий» от выбора базиса. [2]
Сама гомология была разработана как способ анализа и классификации многообразий в соответствии с их циклами – замкнутыми петлями (или, в более общем смысле, подмногообразиями), которые можно нарисовать на данном n- мерном многообразии, но не деформировать непрерывно друг в друга. [3] Эти циклы также иногда представляют собой разрезы, которые можно склеить, или молнии, которые можно застегивать и расстегивать. Циклы классифицируются по размерностям. Например, линия, нарисованная на поверхности, представляет собой 1-цикл, замкнутый контур или (1-многообразие), а поверхность, пересекающая трехмерное многообразие, является 2-циклом.
Поверхности [ править ]
бутылка
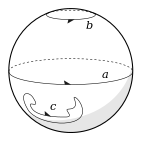
На обычной сфере , цикл b на диаграмме можно сжать к полюсу, и даже большой экваториальный круг a можно сжать таким же образом. Теорема Жордана о кривой показывает, что любой произвольный цикл, такой как c, можно аналогичным образом сжать до точки. Таким образом, все циклы на сфере непрерывно преобразуются друг в друга и принадлежат к одному и тому же классу гомологий. Говорят, что они гомологичны нулю. Разрезание многообразия по циклу, гомологическому нулю, разделяет многообразие на две или более компоненты. Например, если разрезать сферу вдоль a, получится два полушария.
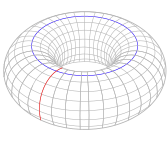
Обычно это не относится к циклам на других поверхностях. Тор имеет циклы, которые не могут непрерывно деформироваться друг в друга, например, на диаграмме ни один из циклов a , b или c не может быть деформирован друг в друга. В частности, циклы a и b нельзя сжать до точки, тогда как цикл c можно, что делает его гомологичным нулю.
Если поверхность тора разрезать вдоль a и b , ее можно развернуть и сплющить в прямоугольник или, что более удобно, в квадрат. Одна противоположная пара сторон представляет разрез по a , а другая противоположная пара представляет разрез по b .
Края квадрата затем можно склеить разными способами. Квадрат можно повернуть, чтобы края сходились в противоположном направлении, как показано стрелками на схеме. Различные способы склеивания сторон дают всего четыре топологически различные поверхности:

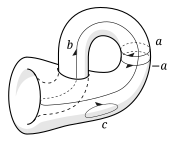
— это бутылка Клейна , представляющая собой тор со скруткой внутри (на квадратной диаграмме скручивание можно рассматривать как разворот нижней стрелки). Это теорема о том, что переклеенная поверхность должна самопересекаться (при погружении в евклидово трехмерное пространство ). Как и тор, циклы a и b не могут быть сокращены, а циклы c можно. Но в отличие от тора, следование b вперед вправо по кругу и назад меняет местами влево и вправо, потому что b случайно пересекает поворот, заданный для одного соединения. Если сделан равноудаленный разрез на одной стороне b , он возвращается на другую сторону и второй раз огибает поверхность, прежде чем вернуться в исходную точку, вырезая скрученную ленту Мёбиуса . Поскольку таким образом локальные лево и право можно произвольно переориентировать, поверхность в целом называется неориентируемой.
Проективная плоскость оба соединения перекручены. Неразрезанная форма, обычно представленная как поверхность Боя , визуально сложна, поэтому на диаграмме показано полусферическое вложение, на котором противоположные точки вокруг края, такие как A и A', идентифицируются как одна и та же точка. Опять же, a является несжимаемым, а c — нет. Если бы b был намотан только один раз, он также был бы несжимаемым и менял бы направление влево и вправо. Однако он заводится во второй раз, при этом снова меняется право и лево; его можно сжать до точки, и он гомологичен c .
Циклы могут быть объединены или сложены вместе, как это было с a и b на торе, когда он был разрезан и сплющен. На бутылки Клейна диаграмме a вращается в одну сторону, а − a вращается в противоположную сторону. Если a рассматривать как разрез, то − a можно рассматривать как операцию склеивания. Разрез и последующая переклейка не меняют поверхность, поэтому a + (− a ) = 0.
Но теперь рассмотрим два a -цикла. Поскольку бутылка Клейна неориентируема, вы можете провезти один из них по всему периметру бутылки (вдоль b -цикла), и он вернется в виде − a . Это связано с тем, что бутылка Клейна сделана из цилиндра, концы a -цикла которого склеены в противоположных направлениях. Следовательно, 2 a = a + a = a + (− a ) = 0. Это явление называется кручением . Аналогично, в проективной плоскости повторный обход несжимаемого цикла b дважды создает тривиальный цикл, который можно сжать до точки; то есть b + b = 0. Поскольку b для достижения нулевого цикла необходимо повторить дважды, говорят, что поверхность имеет коэффициент кручения, равный 2. Однако повторение b -цикла дважды в бутылке Клейна дает просто b + b = 2 b , поскольку этот цикл существует в классе гомологии без кручения. Это соответствует тому, что в фундаментальном многоугольнике бутылки Клейна склеена скруткой только одна пара сторон, тогда как в проективной плоскости скручены обе стороны.
Квадрат — это сжимаемое топологическое пространство , а это означает, что он имеет тривиальные гомологии. Следовательно, дополнительные разрезы отключают его. Квадрат — не единственная фигура на плоскости, которую можно приклеить к поверхности. Например, если склеить противоположные стороны восьмиугольника, получится поверхность с двумя отверстиями. Фактически, все замкнутые поверхности можно получить, склеив стороны некоторого многоугольника, а все многоугольники с четными сторонами (2 n -угольников) можно склеить, чтобы получить разные многообразия. И наоборот, замкнутую поверхность с n ненулевыми классами можно разрезать на 2 n -угольник. Возможны также вариации, например, шестиугольник можно склеить, чтобы получился тор. [4]
Первая известная теория гомологии была опубликована Анри Пуанкаре в его основополагающей статье « Анализ места », J. Ecole Polytech. (2) 1 . 1–121 (1895). В статье представлены классы и отношения гомологии. Возможные конфигурации ориентируемых циклов классифицируются числами Бетти многообразия (числа Бетти являются уточнением эйлеровой характеристики). Классификация неориентируемых циклов требует дополнительной информации о коэффициентах кручения. [3]
Полная классификация 1- и 2-многообразий приведена в таблице.
| Коллектор | Эйлер нет. , час | Ориентируемость | Числа Бетти | Коэффициент кручения (1-мерный) | |||
|---|---|---|---|---|---|---|---|
| Символ [4] | Имя | б 0 | б 1 | б 2 | |||
| Круг (1-коллектор) | 0 | Регулируемый | 1 | 1 | — | — | |
| Сфера | 2 | Регулируемый | 1 | 0 | 1 | Никто | |
| Тор | 0 | Регулируемый | 1 | 2 | 1 | Никто | |
| Проекционная плоскость | 1 | Неориентируемый | 1 | 0 | 0 | 2 | |
| бутылка Клейна | 0 | Неориентируемый | 1 | 1 | 0 | 2 | |
| 2-дырчатый тор | −2 | Регулируемый | 1 | 4 | 1 | Никто | |
| g -дырчатый тор ( g — род ) | 2-2 г | Регулируемый | 1 | 2 г | 1 | Никто | |
| Сфера с поперечными колпачками | 2 - с | Неориентируемый | 1 | с - 1 | 0 | 2 | |
| 2-Коллектор с отверстиями g и c перемычками ( c > 0) | 2 - (2 г + с ) | Неориентируемый | 1 | (2 г + с ) - 1 | 0 | 2 | |
- Примечания
- Для неориентируемой поверхности отверстие эквивалентно двум перемычкам.
- Любое 2-многообразие представляет собой связную сумму g торов и c проективных плоскостей. Для сферы , г = с = 0.
Обобщение [ править ]
Многообразие с краем или открытое многообразие топологически отличается от закрытого многообразия и может быть создано путем разрезания любого подходящего закрытого многообразия. Например диск или 2-шар. ограничен кругом . Его можно создать, разрезав тривиальный цикл в любом двумерном многообразии и оставив его фрагмент удаленным, проткнув сферу и растянув прокол в ширину, или разрезав проективную плоскость. Это также можно рассматривать как заполнение круга на плоскости.
Когда два цикла могут непрерывно деформироваться друг в друга, то разрезание по одному дает ту же форму, что и разрезание по другому, вплоть до некоторого изгиба и растяжения. В этом случае говорят, что два цикла гомологичны или принадлежат одному и тому же классу гомологии . Кроме того, если один цикл можно непрерывно деформировать в комбинацию других циклов, то резка по начальному циклу аналогична резке по комбинации других циклов. Например, разрез по восьмерке эквивалентен разрезу по двум ее лепесткам. В этом случае говорят, что цифра 8 гомологична сумме своих долей.
Два открытых многообразия с одинаковыми границами (с точностью до некоторого изгиба и растяжения) можно склеить вместе, чтобы образовать новое многообразие, которое является их связной суммой.
Этот геометрический анализ многообразий не является строгим. В поисках большей строгости Пуанкаре разработал симплициальные гомологии триангулированного многообразия и создал то, что сейчас называется цепным комплексом . [6] [7] Эти цепные комплексы (поскольку они сильно обобщены) составляют основу большинства современных трактовок гомологии.
В таких обработках цикл не обязательно должен быть непрерывным: 0-цикл представляет собой набор точек, и разрезание по этому циклу соответствует прокалыванию многообразия. 1-цикл соответствует набору замкнутых петель (образ 1-многообразия ). На поверхности резка по 1-циклу дает либо несвязные куски, либо более простую форму. 2-цикл соответствует набору вложенных поверхностей, таких как сфера или тор и т. д.
Эмми Нётер и независимо Леопольд Виеторис и Вальтер Майер развили теорию алгебраических групп гомологии в период 1925–28. [8] [9] [10] Новая комбинаторная топология формально рассматривала топологические классы как абелевы группы . Группы гомологий — это конечно порожденные абелевы группы, а классы гомологий — элементы этих групп. Числа Бетти многообразия представляют собой ранг свободной части группы гомологий, а неориентируемые циклы описываются периодической частью.
Последующее распространение групп гомологии привело к изменению терминологии и точки зрения от «комбинаторной топологии» к « алгебраической топологии ». [11] Алгебраические гомологии остаются основным методом классификации многообразий. [12]
Неофициальные примеры [ править ]
Гомологии топологического пространства X - это набор топологических инвариантов X, представленных его группами гомологии.
Одномерная сфера это круг . Он имеет единственный связный компонент и дырку с одномерной границей, но не имеет дыр более высокой размерности. Соответствующие группы гомологии имеют вид
Двумерная сфера имеет единственную связную компоненту, не имеет дырок с одномерной границей, дырок с двумерной границей и дыр с более высокой размерностью. Соответствующие группы гомологий: [14] [15]
В общем случае для n -мерной сферы группы гомологии
Двумерный шар это цельный диск. Он имеет единственный компонент, связанный по траектории, но, в отличие от круга, не имеет отверстий более высокой размерности. Все соответствующие группы гомологий тривиальны, за исключением . В общем случае для n -мерного шара [14]
Тор . определяется как произведение двух окружностей . Тор имеет единственную компоненту связности путей, две независимые одномерные дыры (обозначены красными и синими кружками) и одну двумерную дыру, служащую внутренней частью тора. Соответствующие группы гомологий: [16]
Если n произведений топологического пространства X записывается как , то, вообще говоря, для n -мерного тора ,
( см. в разделе Тор#n-мерный тор и число Бетти#Больше примеров более подробную информацию ).
Две независимые одномерные дыры образуют независимые генераторы в конечно порожденной абелевой группе, выраженной как группа произведений
Для проективной плоскости P простое вычисление показывает (где – циклическая группа порядка 2): [17]
соответствует, как и в предыдущих примерах, тому факту, что имеется единственная компонента связности. — это новое явление: интуитивно оно соответствует тому факту, что существует единственная несжимаемая «петля», но если мы проделаем цикл дважды, она станет сжимаемой до нуля. Это явление называется кручением .
Построение гомологий групп
Следующий текст описывает общий алгоритм построения групп гомологий. Возможно, читателю будет проще сначала рассмотреть несколько простых примеров: гомологии графов и симплициальные гомологии .
Общая конструкция начинается с такого объекта, как топологическое пространство X , на котором сначала определяется цепной комплекс C ( X кодирующий информацию о X. ) , Цепной комплекс — это последовательность абелевых групп или модулей. . связаны гомоморфизмами которые называются граничными операторами . [16] То есть,
где 0 обозначает тривиальную группу и при i < 0. Требуется также, чтобы композиция любых двух последовательных граничных операторов была тривиальна. То есть для n всех
т. е. постоянная карта, отправляющая каждый элемент групповой идентичности в
Утверждение о том, что граница границы тривиальна, эквивалентно утверждению, что , где обозначает образ граничного оператора и его ядро . Элементы называются границами и элементами называются циклами .
Поскольку каждая цепная группа Cn абелева , все ее подгруппы нормальны. Тогда потому что является подгруппой C n , абелева, и поскольку поэтому является нормальной подгруппой . Тогда можно создать факторгруппу
называется n- й группой гомологии X . Элементы Hn . ( X называются классами гомологий ) Каждый класс гомологии является классом эквивалентности над циклами, и два цикла в одном классе гомологии называются гомологичными . [18]
Цепной комплекс называется точным, если образ ( n +1)-го отображения всегда равен ядру n- го отображения. Таким образом, группы гомологий X измеряют, «насколько далек» цепной комплекс, связанный с X , от точности. [19]
Приведенные группы гомологии цепного комплекса C ( X ) определяются как гомологии расширенного цепного комплекса [20]
где граничный оператор является
для комбинации очков которые являются фиксированными генераторами C 0 . Приведенные группы гомологии совпадают с для Дополнительный в цепном комплексе представлена уникальная карта от пустого симплекса к X .
Вычисление цикла и граница группы обычно довольно сложны, так как они имеют очень большое количество образующих. С другой стороны, есть инструменты, которые облегчают задачу.
Группы симплициальных гомологий свободная H n ( X ) симплициального комплекса X определяются с использованием симплициального цепного комплекса ( X ) , где C n ( X ) — абелева группа, порожденная n -симплексами X. C см. в симплициальной гомологии Подробности .
Сингулярные гомологий группы H n ( X ) определены для любого топологического пространства X и согласуются с симплициальными группами гомологий для симплициального комплекса.
Группы когомологий формально подобны группам гомологий: все начинается с коцепного комплекса , который аналогичен цепному комплексу, но чьи стрелки теперь обозначаются указать в направлении увеличения n, а не уменьшения n ; затем группы коциклов и кограниц следуют из того же описания. я группа Тогда n- когомологий X является факторгруппой
по аналогии с n-й группой гомологии.
Гомология гомотопии против
Гомотопические группы подобны группам гомологий в том, что они могут представлять «дыры» в топологическом пространстве. Существует тесная связь между первой гомотопической группой и первая группа гомологий : последнее есть абелианизация первого. Следовательно, говорят, что «гомология является коммутативной альтернативой гомотопии». [21] : 4:00 Высшие гомотопические группы абелевы и связаны с группами гомологий теоремой Гуревича , но могут быть значительно более сложными. Например, гомотопические группы сфер плохо изучены и вообще не известны, в отличие от прямого описания групп гомологий, данного выше.
Например, пусть X — восьмерка . Его первая гомотопическая группа представляет собой группу направленных петель, начинающихся и заканчивающихся в заданной точке (например, в ее центре). Это эквивалентно свободной группе ранга 2, которая не является коммутативной: цикл по самому левому циклу, а затем по самому правому циклу отличается от цикла по самому правому циклу, а затем по самому левому циклу. Напротив, его первая группа гомологии группа разрезов, выполненных на поверхности. Эта группа коммутативна, поскольку (неформально) разрезание самого левого цикла, а затем самого правого цикла приводит к тому же результату, что и разрезание самого правого цикла, а затем самого левого цикла.
Типы гомологии [ править ]
Различные типы теории гомологии возникают в результате отображения функторов различных категорий математических объектов в категорию цепных комплексов. В каждом случае композиция функтора от объектов к цепным комплексам и функтора от цепных комплексов к группам гомологий определяет общий функтор гомологий теории. [22]
Симплициальная гомология [ править ]
Мотивирующий пример взят из топологии : симплициальные гомологии симплициального комплекса X. алгебраической Здесь цепная группа Cn — это свободная абелева группа или модуль, генераторами которого являются - мерные ориентированные симплексы X. n комплекса Ориентация определяется путем упорядочивания вершин и выражения ориентированного симплекса. как n -кортеж его вершин перечислены в порядке возрастания (т.е. в порядке вершин комплекса, где это вершина, появляющаяся в кортеже). Отображение из Cn называется в Cn −1 граничным отображением и отправляет симплекс
который считается 0, если Такое поведение генераторов индуцирует гомоморфизм на всем следующим Cn образом. Учитывая элемент , запишите его как сумму образующих где представляет собой набор n -симплексов в X , а m i - коэффициенты из кольца C n , определенного над (обычно целыми числами, если не указано иное). Затем определите
Размерность n -й гомологии X оказывается числом «дырок» в X в размерности n . Его можно вычислить, приведя матричные представления этих граничных отображений в нормальную форму Смита .
Сингулярные гомологии [ править ]
Используя пример симплициальной гомологии в качестве модели, можно определить сингулярную гомологию для любого топологического пространства X . Цепной комплекс для X определяется путем взятия C n в качестве свободной абелевой группы (или свободного модуля), генераторами которой являются все непрерывные отображения n -мерных симплексов в X . Гомоморфизмы ∂ n возникают из граничных отображений симплексов.
Групповая гомология [ править ]
В абстрактной алгебре гомологии используются для определения производных функторов , например функторов Tor . мы начинаем с некоторого ковариантного аддитивного функтора F и некоторого модуля X. Здесь Цепной комплекс для X определяется следующим образом: сначала найдите свободный модуль и сюръективный гомоморфизм Затем можно найти бесплатный модуль и сюръективный гомоморфизм Продолжая в том же духе, последовательность бесплатных модулей и гомоморфизмы можно определить. Применяя к этой последовательности функтор F , получаем цепной комплекс; гомология этого комплекса зависит только от F и X и по определению является n м производным функтором F , примененным к X. -
Обычное использование групповых (ко) гомологий заключается в классификации возможных групп расширений E , которые содержат данный G -модуль M как нормальную подгруппу и имеют данную факторгруппу G , так что
теории гомологии Другие
Функторы гомологии
Цепные комплексы образуют категорию : Морфизм цепного комплекса ( ) к цепному комплексу ( ) — последовательность гомоморфизмов такой, что для всех н . - ю n гомологии H n можно рассматривать как ковариантный функтор из категории цепных комплексов в категорию абелевых групп (или модулей).
Если цепной комплекс зависит от объекта X ковариантным образом (это означает, что любой морфизм индуцирует морфизм цепного комплекса X в цепной комплекс Y ), то H n являются ковариантными функторами из категории, которой принадлежит X , в категорию абелевых групп (или модулей).
Единственное различие между гомологиями и когомологиями состоит в том, что в когомологиях цепные комплексы контравариантным образом зависят от X и, следовательно, группы гомологий (которые в этом контексте называются группами когомологий и обозначаются H н ) образуют контравариантные функторы из категории, которой принадлежит X , в категорию абелевых групп или модулей.
Свойства [ править ]
Если ( ) — цепной комплекс такой, что все An, кроме конечного числа, равны нулю , а остальные являются конечно порожденными абелевыми группами (или конечномерными векторными пространствами), то мы можем определить эйлерову характеристику
(с использованием ранга в случае абелевых групп и размерности Гамеля в случае векторных пространств). Оказывается, эйлерову характеристику можно вычислить и на уровне гомологии:
и, особенно в алгебраической топологии, это дает два способа вычисления важного инварианта для объекта X , породившего цепной комплекс.
Каждая короткая точная последовательность
цепных комплексов дает длинную точную последовательность групп гомологии
Все отображения в этой длинной точной последовательности индуцируются отображениями между цепными комплексами, за исключением отображений Последние называются связующими гомоморфизмами и обеспечиваются леммой о зигзаге . Эту лемму можно применять к гомологии множеством способов, которые помогают вычислить группы гомологии, например теории относительной гомологии и последовательности Майера-Вьеториса .
Приложения [ править ]
Применение в чистой математике [ править ]
Известные теоремы, доказанные с использованием гомологии, включают следующее:
- : Теорема Брауэра о неподвижной точке если f — любое непрерывное отображение шара B н сам по себе, то существует фиксированная точка с
- Инвариантность области : если U является открытым подмножеством и — инъективное непрерывное отображение , то открыто f — гомеоморфизм между U и V. и
- Теорема о волосатом шаре : любое непрерывное векторное поле на 2-сфере (или, в более общем плане, на 2 - сфере для любого ) в какой-то момент исчезает.
- Теорема Борсука -Улама : любая непрерывная функция из n -сферы в евклидово n -пространство отображает некоторую пару противоположных точек в одну и ту же точку. (Две точки на сфере называются антиподальными, если они расположены точно в противоположных направлениях от центра сферы.)
- Инвариантность размерности: если непустые открытые подмножества и гомеоморфны, то [23]
Применение в науке и технике [ править ]
В топологическом анализе данных наборы данных рассматриваются как выборка облака точек многообразия или алгебраического многообразия, встроенная в евклидово пространство . Связывая точки ближайших соседей в облаке в триангуляцию, создается симплициальная аппроксимация многообразия и можно вычислить его симплициальные гомологии. Поиск методов надежного расчета гомологии с использованием различных стратегий триангуляции в нескольких масштабах длины является темой устойчивой гомологии . [24]
В сенсорных сетях датчики могут передавать информацию через специальную сеть, которая динамически меняется во времени. Чтобы понять глобальный контекст этого набора локальных измерений и путей связи, полезно вычислить гомологию топологии сети , чтобы оценить, например, дыры в покрытии. [25]
В динамических систем теории в физике Пуанкаре был одним из первых, кто рассмотрел взаимодействие между инвариантным многообразием динамической системы и ее топологическими инвариантами. Теория Морса связывает динамику градиентного потока на многообразии, например, с его гомологиями. Гомологии Флоера распространили это на бесконечномерные многообразия. Теорема КАМ установила, что периодические орбиты могут следовать по сложным траекториям; в частности, они могут образовывать косы , которые можно исследовать с помощью гомологии Флоера. [26]
В одном классе методов конечных элементов может потребоваться решение краевых задач для дифференциальных уравнений, включающих оператор Ходжа-Лапласа , в топологически нетривиальных областях, например, в электромагнитном моделировании . В этих симуляциях решению помогает фиксация класса когомологий решения на основе выбранных граничных условий и гомологии области. Домены FEM можно триангулировать, на основе чего можно рассчитать симплициальную гомологию. [27] [28]
Программное обеспечение [ править ]
Для расчета групп гомологии конечных клеточных комплексов были разработаны различные пакеты программного обеспечения. Linbox — библиотека C++ для выполнения быстрых матричных операций, включая нормальную форму Смита ; он взаимодействует как с Gap , так и с Maple . Chomp , CAPD::Redhom и Perseus также написаны на C++. Все три реализуют алгоритмы предварительной обработки, основанные на простой гомотопической эквивалентности и дискретной теории Морса, для выполнения сохраняющих гомологию сокращений входных комплексов ячеек, прежде чем прибегать к матричной алгебре. Kenzo помимо гомологии его можно также использовать для генерации представлений гомотопических написан на Лиспе, и групп конечных симплициальных комплексов. Gmsh включает в себя решатель гомологии для сеток конечных элементов, который может генерировать базы когомологий, которые можно напрямую использовать в программном обеспечении конечных элементов. [27]
Примечания [ править ]
- ^ частично от греческого ὁμός homos «идентичный»
См. также [ править ]
- Номер Бетти
- Велосипедное пространство
- Когомологии Де Рама
- Аксиомы Эйленберга – Стинрода
- Чрезвычайная теория гомологии
- Гомологическая алгебра
- Гомологические гипотезы в коммутативной алгебре
- Гомологическая связность
- Гомологическое измерение
- Гомотопическая группа
- Теорема Кюннета
- Список теорий гомологии - также есть список теорий гомологии.
- Двойственность Пуанкаре
Ссылки [ править ]
- ^ Стиллвелл 1993 , с. 170
- ^ Weibel 1999 , стр. 2–3 (в PDF)
- ↑ Перейти обратно: Перейти обратно: а б Ричесон 2008 , с. 254
- ↑ Перейти обратно: Перейти обратно: а б Уикс, Джеффри Р. (2001). Форма пространства . ЦРК Пресс. ISBN 978-0-203-91266-9 .
- ^ Ричесон 2008
- ^ Ричесон 2008 , с. 258
- ^ Вейбель 1999 , с. 4
- ^ Хилтон 1988 , с. 284
- ^ Например, появление понятия группы гомологии Николя Басбуа (PDF) на французском языке, примечание 41, прямо называет Нётер изобретателем группы гомологии.
- ^ Хирцебрух, Фридрих, Эмми Нётер и топология в Teicher 1999 , стр. 61–63.
- ^ Бурбаки и алгебраическая топология Джона Макклири (PDF). Архивировано 23 июля 2008 г. в Wayback Machine, содержит документацию (переведенную на английский язык с французских оригиналов).
- ^ Ричесон 2008 , с. 264
- ^ Спаниер 1966 , с. 155
- ↑ Перейти обратно: Перейти обратно: а б с Гауэрс, Barrow-Green & Leader 2010 , стр. 390–391.
- ^ Вильдбергер, Норман Дж. (2012). «Больше вычислений гомологии» . Ютуб . Архивировано из оригинала 11 декабря 2021 г.
- ↑ Перейти обратно: Перейти обратно: а б Хэтчер 2002 , с. 106
- ^ Вильдбергер, Норман Дж. (2012). «Дельта-комплексы, числа Бетти и кручение» . Ютуб . Архивировано из оригинала 11 декабря 2021 г.
- ^ Хэтчер 2002 , стр. 105–106.
- ^ Хэтчер 2002 , с. 113
- ^ Хэтчер 2002 , с. 110
- ^ Вильдбергер, Нью-Джерси (2012). «Введение в гомологию» . Ютуб . Архивировано из оригинала 11 декабря 2021 г.
- ^ Спаниер 1966 , с. 156
- ^ Хэтчер 2002 , с. 126.
- ^ «Обзор CompTop» . Проверено 16 марта 2014 г.
- ^ «Роберт Грист: прикладная топология» . Проверено 16 марта 2014 г.
- ^ ван ден Берг, JB; Грист, Р.; Вандерворст, Колорадо; Войчик, В. (2015). «Гомология Брейда Флоера» (PDF) . Журнал дифференциальных уравнений . 259 (5): 1663–1721. Бибкод : 2015JDE...259.1663V . дои : 10.1016/j.jde.2015.03.022 . S2CID 16865053 .
- ↑ Перейти обратно: Перейти обратно: а б Пелликка, М; С. Сууриниеми; Л. Кеттунен; К. Гезен (2013). «Вычисление гомологии и когомологии при моделировании методом конечных элементов» (PDF) . СИАМ J. Sci. Вычислить . 35 (5): Б1195–Б1214. Бибкод : 2013ГАК...35Б1195П . CiteSeerX 10.1.1.716.3210 . дои : 10.1137/130906556 .
- ^ Арнольд, Дуглас Н.; Ричард С. Фальк; Рагнар Винтер (16 мая 2006 г.). «Внешнее исчисление конечных элементов, гомологические методы и приложения» . Акта Нумерика . 15 :1–155. Бибкод : 2006AcNum..15....1A . дои : 10.1017/S0962492906210018 . S2CID 122763537 .
Дальнейшее чтение [ править ]
- Картан, Анри Поль ; Эйленберг, Сэмюэл (1956). Гомологическая алгебра . Принстонский математический ряд. Том. 19. Издательство Принстонского университета. ISBN 9780674079779 . OCLC 529171 .
- Эйленберг, Сэмюэл; Мур, Дж. К. (1965). Основы относительной гомологической алгебры . Мемуары Американского математического общества. Том. 55. Американское математическое общество. ISBN 9780821812556 . ОСЛК 1361982 .
- Гауэрс, Тимоти ; Барроу-Грин, июнь ; Лидер, Имре, ред. (2010), Принстонский спутник математики , Princeton University Press, ISBN 9781400830398 .
- Хэтчер, А. (2002), Алгебраическая топология , издательство Кембриджского университета, ISBN 0-521-79540-0 . Подробное обсуждение теорий гомологии симплициальных комплексов и многообразий, сингулярных гомологии и т. д.
- Хилтон, Питер (1988), «Краткая субъективная история гомологии и теории гомотопии в этом столетии», Mathematics Magazine , 60 (5), Mathematical Association of America: 282–291, doi : 10.1080/0025570X.1988.11977391 , JSTOR 2689545
- Ричесон, Д. (2008), Жемчужина Эйлера: формула многогранника и рождение топологии , Принстонский университет .
- Спэньер, Эдвин Х. (1966), Алгебраическая топология , Спрингер, стр. 155, ISBN 0-387-90646-0 .
- Стиллвелл, Джон (1993), «Теория гомологии и абелианизация», Классическая топология и комбинаторная теория групп , Тексты для аспирантов по математике, том. 72, Спрингер, стр. 169–184, номер документа : 10.1007/978-1-4612-4372-4_6 , ISBN. 978-0-387-97970-0 .
- Тейчер, М. , изд. (1999), Наследие Эмми Нётер , Материалы Израильской математической конференции, Университет Бар-Илан / Американское математическое общество / Oxford University Press , ISBN 978-0-19-851045-1 , OCLC 223099225
- Вейбель, Чарльз А. (1999), «28. История гомологической алгебры» (PDF) , в Джеймсе, IM (ред.), История топологии , Elsevier, ISBN 9780080534077 .
Внешние ссылки [ править ]
- Группа гомологии в Математической энциклопедии
- [1] Н. Дж. Виндбергер: введение в алгебраическую топологию, последние шесть лекций с простым введением в гомологию.
- [2] Алгебраическая топология Аллен Хэтчер - Глава 2 о гомологии

























































![{\displaystyle [\emptyset ]\longrightarrow X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ce21624866825d0c90e1d5a93ddd41cc74d43fa)









![{\displaystyle (\sigma [0],\sigma [1],\dots,\sigma [n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9893cb6a42a8658098e94b07b7b017fcbf48b942)
![{\displaystyle \sigma [0]<\sigma [1]<\cdots <\sigma [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eeaa6286bd46a6c0ab76d0920a115a03216aa57)
![{\displaystyle \sigma [я]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48f6feb944eb1c860bd78391bccee81f01f4bd93)


![{\displaystyle \sigma =(\sigma [0],\sigma [1],\dots,\sigma [n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7145641dc88fcdeaf628fe229c7a6d5c5857ac57)
![{\displaystyle \partial _ {n}(\sigma)=\sum _{i=0}^{n}(-1)^{i}\left(\sigma [0],\dots,\sigma [i -1],\sigma [i+1],\dots ,\sigma [n]\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1adc96f7f6d2efdd0ba4e7ed003441ebd6e3d32f)


































