Эксперимент Штерна-Герлаха

В квантовой физике эксперимент Штерна-Герлаха что пространственная ориентация углового момента квантуется продемонстрировал , . Таким образом, было показано, что система атомного масштаба обладает внутренне квантовыми свойствами. В оригинальном эксперименте атомы серебра были отправлены через пространственно изменяющееся магнитное поле , которое отклоняло их до того, как они попадали на экран детектора, например, на предметное стекло. Частицы с ненулевым магнитным моментом отклонялись из-за градиента магнитного поля от прямолинейного пути. На экране были видны отдельные точки накопления, а не непрерывного распределения. ^[1] из-за их квантованного спина . Исторически этот эксперимент сыграл решающую роль в убеждении физиков в реальности квантования углового момента во всех системах атомного масштаба. ^[2]^[3]^[4]

После концепции Отто Штерна в 1921 году эксперимент впервые был успешно проведен с Вальтером Герлахом в начале 1922 года. ^[1]^[5]^[6]

Описание

Видео, объясняющее квантовый спин по сравнению с классическим магнитом в эксперименте Штерна-Герлаха

Эксперимент Штерна-Герлаха включает в себя отправку атомов серебра через неоднородное магнитное поле и наблюдение за их отклонением. Атомы серебра испарялись с помощью электрической печи в вакууме. С помощью тонких щелей атомы направлялись в плоский луч, который проходил через неоднородное магнитное поле, прежде чем столкнуться с металлической пластиной. Законы классической физики предсказывают, что совокупность конденсированных атомов серебра на пластине должна образовать тонкую сплошную линию той же формы, что и исходный луч. Однако неоднородное магнитное поле привело к тому, что луч разделился на два отдельных направления, создав две линии на металлической пластине.

Результаты показывают, что частицы обладают собственным угловым моментом , который очень похож на угловой момент классически вращающегося объекта, но принимает только определенные квантованные значения. Другой важный результат заключается в том, что одновременно можно измерить только одну составляющую спина частицы, а это означает, что измерение спина по оси z уничтожает информацию о вращении частицы по осям x и y.

Эксперимент обычно проводится с использованием электрически нейтральных частиц, таких как атомы серебра. Это позволяет избежать большого отклонения на пути заряженной частицы, движущейся через магнитное поле, и позволяет доминировать эффектам, зависящим от спина. ^[7]^[8]

Если частицу рассматривать как классический вращающийся магнитный диполь , она будет прецессировать в магнитном поле из-за крутящего момента, который магнитное поле оказывает на диполь (см. прецессию, вызванную крутящим моментом ). Если она движется в однородном магнитном поле, силы, действующие на противоположные концы диполя, компенсируют друг друга, и траектория частицы не изменяется. Однако если магнитное поле неоднородно, то сила на одном конце диполя будет немного больше, чем противодействующая сила на другом конце, так что существует результирующая сила, которая отклоняет траекторию частицы. Если бы частицы были классическими вращающимися объектами, можно было бы ожидать, что распределение векторов их спинового углового момента будет случайным и непрерывным . Каждая частица будет отклоняться на величину, пропорциональную скалярному произведению ее магнитного момента с градиентом внешнего поля, создавая некоторое распределение плотности на экране детектора. Вместо этого частицы, проходящие через аппарат Штерна-Герлаха, отклоняются вверх или вниз на определенную величину. Это было измерение квантов наблюдаемая, теперь известная как спиновый угловой момент, которая продемонстрировала возможные результаты измерения, когда наблюдаемая имеет дискретный набор значений или точечный спектр .

Хотя некоторые дискретные квантовые явления, такие как атомные спектры , наблюдались гораздо раньше, эксперимент Штерна-Герлаха позволил ученым впервые в истории науки напрямую наблюдать разделение между дискретными квантовыми состояниями.

Теоретически квантовый угловой момент любого вида имеет дискретный спектр , который иногда кратко выражают как «квантуется угловой момент » .

Экспериментируйте с частицами со спином +1/2 или −1/2.

Если эксперимент проводится с использованием заряженных частиц, таких как электроны, возникнет сила Лоренца , стремящаяся искривить траекторию по кругу. Эту силу можно нейтрализовать электрическим полем соответствующей величины, ориентированным поперек траектории заряженной частицы.

Электроны — это частицы со спином 1/2 . У них есть только два возможных значения спинового углового момента, измеренные вдоль любой оси: $+{\frac {\hbar }{2}}$ или $-{\frac {\hbar }{2}}$ , чисто квантовомеханическое явление. Поскольку его значение всегда одинаково, оно считается внутренним свойством электронов и иногда называется «собственным угловым моментом» (чтобы отличить его от орбитального углового момента, который может меняться и зависит от присутствия других частиц). Если измерить вращение вдоль вертикальной оси, электроны описываются как «спин вверх» или «спин вниз», в зависимости от магнитного момента, направленного вверх или вниз соответственно.

Математически описать эксперимент со спином $+{\frac {1}{2}}$ частиц, проще всего использовать Дирака Бракета обозначение . Когда частицы проходят через устройство Штерна-Герлаха, они отклоняются вверх или вниз и наблюдаются детектором, который решает либо увеличить, либо уменьшить вращение. Они описываются квантовым числом углового момента $j$ , который может принимать одно из двух возможных разрешенных значений: $+{\frac {\hbar }{2}}$ или $-{\frac {\hbar }{2}}$ . Наблюдение (измерение) импульса вдоль $z$ ось соответствует оператору $J_{z}$ . ^{[ указать ]} В математических терминах начальное состояние частиц есть

|\psi \rangle =c_{1}\left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle +c_{2}\left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle

где константы $c_{1}$ и $c_{2}$ являются комплексными числами. Этот спин начального состояния может указывать в любом направлении. Квадраты абсолютных значений $|c_{1}|^{2}$ и $|c_{2}|^{2}$ определить вероятности того, что для системы в исходном состоянии $|\psi \rangle$ одно из двух возможных значений $j$ находится после проведения измерения. Константы $c_{1}$ и $c_{2}$ также необходимо нормализовать, чтобы вероятность нахождения любого из значений была равна единице, то есть мы должны гарантировать, что $|c_{1}|^{2}+|c_{2}|^{2}=1$ . Однако этой информации недостаточно для определения значений $c_{1}$ и $c_{2}$ , потому что это комплексные числа. Следовательно, измерение дает только квадраты величин констант, которые интерпретируются как вероятности.

Последовательные эксперименты

Если мы свяжем несколько аппаратов Штерна-Герлаха (прямоугольники, содержащие SG ), мы ясно увидим, что они не действуют как простые селекторы, т.е. отфильтровывают частицы с одним из состояний (существовавших ранее до измерения) и блокируют другие. Вместо этого они изменяют состояние, наблюдая за ним (как в случае с поляризацией света ). На рисунке ниже x и z обозначают направления (неоднородного) магнитного поля, причем плоскость xz ортогональна пучку частиц. В трех системах СГ, показанных ниже, заштрихованные квадраты обозначают блокировку данного выхода, т.е. каждая из систем СГ с блокировщиком позволяет только частицам с одним из двух состояний войти в следующий аппарат СГ в последовательности. ^[9]

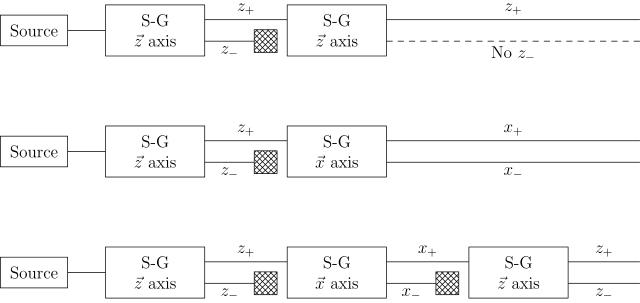
Эксперимент 1

На верхнем рисунке показано, что когда второй, идентичный аппарат СГ размещен на выходе первого аппарата, виден только z+ на выходе второго аппарата . Этот результат является ожидаемым, поскольку ожидается, что все нейтроны в этот момент будут иметь спин z+, поскольку только луч z+ из первого аппарата вошел во второй аппарат. ^[10]

Эксперимент 2

Средняя система показывает, что происходит, когда на выходе луча z+ размещается другое устройство SG, в результате чего первое устройство измеряет отклонение лучей по оси x вместо оси z. Второе устройство выдает выходные данные x+ и x-. Классически мы ожидаем, что один луч будет иметь характеристику x, ориентированную + и характеристику z, ориентированную +, а другой - характеристику x, ориентированную - и характеристику z, ориентированную +. ^[10]

Эксперимент 3

Нижняя система противоречит этому ожиданию. Выходные данные третьего устройства, которое измеряет отклонение по оси z, снова показывают выходные данные как z- , так и z+. Учитывая, что входные данные второго аппарата СГ состояли только из z+ , можно сделать вывод, что аппарат СГ должен изменять состояния частиц, которые проходят через него. Этот эксперимент можно интерпретировать как демонстрацию принципа неопределенности : поскольку угловой момент не может быть измерен в двух перпендикулярных направлениях одновременно, измерение углового момента в направлении x разрушает предыдущее определение углового момента в направлении z. Вот почему третий прибор измеряет обновленные лучи z+ и z-, как будто измерение x фактически полностью очистило выходной сигнал z+. ^[10]

История

Мемориальная доска во Франкфуртском институте в память об эксперименте.

Эксперимент Штерна-Герлаха был задуман Отто Штерном в 1921 году и проведен им и Вальтером Герлахом во Франкфурте в 1922 году. ^[9] На момент эксперимента наиболее распространенной моделью описания атома была модель Бора-Зоммерфельда , ^[11]^[12] которая описывала электроны как движущиеся вокруг положительно заряженного ядра только на определенных дискретных атомных орбиталях или энергетических уровнях . Поскольку электрон был квантован так , чтобы находиться только в определенных положениях в пространстве, разделение на отдельные орбиты называлось пространственным квантованием . Эксперимент Штерна-Герлаха был призван проверить гипотезу Бора-Зоммерфельда о том, что направление углового момента атома серебра квантовано. ^[13]

Впервые эксперимент был проведен с электромагнитом, который позволял постепенно включать неоднородное магнитное поле от нулевого значения. ^[1] Когда поле было нулевым, атомы серебра осаждалися на предметном стекле в виде одной полосы. Когда поле усилилось, середина полосы начала расширяться и в конечном итоге разделиться на две части, так что изображение на предметном стекле стало похоже на отпечаток губы с отверстием посередине и закрытием на обоих концах. ^[14] В середине, где магнитное поле было достаточно сильным, чтобы разделить луч на две части, статистически половина атомов серебра отклонилась из-за неоднородности поля.

Отметим, что эксперимент был проведен за несколько лет до того, как Джордж Уленбек и Сэмюэл Гаудсмит сформулировали свою гипотезу о существовании спина электрона в 1925 году. ^[15] Хотя позже выяснилось, что результат эксперимента Штерна-Герлаха согласуется с предсказаниями квантовой механики для частицы со спином 1/2, экспериментальный результат также согласуется с теорией Бора-Зоммерфельда . ^[16]

В 1927 году Т. Э. Фиппс и Дж. Б. Тейлор воспроизвели этот эффект, используя атомы водорода в основном состоянии , тем самым устранив любые сомнения, которые могли быть вызваны использованием атомов серебра . ^[17] Однако в 1926 году нерелятивистское скалярное уравнение Шрёдингера неверно предсказало, что магнитный момент водорода будет равен нулю в его основном состоянии. Чтобы исправить эту проблему, Вольфганг Паули рассмотрел версию уравнения Шредингера со спином 1/2, используя три матрицы Паули , которые теперь носят его имя, что, как позже было показано Полем Дираком в 1928 году, является следствием его релятивистского уравнения Дирака .

В начале 1930-х годов Штерн вместе с Отто Робертом Фришем и Иммануэлем Эстерманном усовершенствовал аппаратуру молекулярного пучка, достаточную для измерения магнитного момента протона , величины почти в 2000 раз меньшей, чем момент электрона. В 1931 году теоретический анализ, проведенный Грегори Брейтом и Исидором Исааком Раби, показал, что этот прибор можно использовать для измерения ядерного спина всякий раз, когда была известна электронная конфигурация атома. Эта концепция была применена Раби и Виктором Коэнами в 1934 году для определения $3/2$ спин атомов Na. ^[18]

В 1938 году Раби и его коллеги вставили в свой аппарат элемент колеблющегося магнитного поля, изобретя спектроскопию ядерного магнитного резонанса . ^[19]^[20] Настроив частоту генератора на частоту ядерной прецессии, они могли избирательно настраиваться на каждый квантовый уровень исследуемого материала. За эту работу Лави был удостоен Нобелевской премии в 1944 году. ^[21]

Важность

Эксперимент Штерна-Герлаха сильно повлиял на более поздние разработки в современной физике :

В последующее десятилетие ученые, используя аналогичные методы, показали, что ядра некоторых атомов также обладают квантованным угловым моментом. ^{[ нужен пример ]} Именно взаимодействие этого ядерного углового момента со спином электрона отвечает за сверхтонкую структуру спектроскопических линий. ^[22]
В 1930-х годах, используя расширенную версию аппарата Штерна-Герлаха, Исидор Раби и его коллеги показали, что, используя изменяющееся магнитное поле, можно заставить магнитный момент переходить из одного состояния в другое. ^{[ нужна ссылка ]} Серия экспериментов достигла кульминации в 1937 году, когда они обнаружили, что переходы между состояниями могут быть вызваны с помощью изменяющихся во времени полей или радиочастотных полей . Так называемые колебания Раби — это рабочий механизм оборудования магнитно-резонансной томографии, используемого в больницах. ^{[ нужна ссылка ]}
Норман Ф. Рэмси позже модифицировал аппарат Раби, чтобы увеличить время взаимодействия с полем. Чрезвычайная чувствительность, обусловленная частотой излучения, делает его очень полезным для поддержания точного времени, и он до сих пор используется в атомных часах . ^{[ нужна ссылка ]}
В начале шестидесятых годов Рэмси и Дэниел Клеппнер использовали систему Штерна-Герлаха для получения луча поляризованного водорода в качестве источника энергии для водородного мазера , который до сих пор является одним из самых популярных стандартов частоты .
Непосредственное наблюдение спина является наиболее прямым свидетельством квантования в квантовой механике. ^{[ почему? ]} ^{[ нужна ссылка ]}
Эксперимент Штерна-Герлаха стал прототипом ^[23]^[24]^[25] для квантовых измерений , демонстрирующих наблюдение единственного реального значения ( собственного значения ) изначально неизвестного физического свойства. На входе в магнит Штерна-Герлаха направление магнитного момента атома серебра неопределенно, но наблюдается либо параллельное, либо антипараллельное направлению магнитного поля B на выходе из магнита. Атомы с магнитным моментом, параллельным B, были ускорены в этом направлении градиентом магнитного поля; те, у кого моменты антипараллельны, ускорялись в обратную сторону. Таким образом, каждый атом, проходящий через магнит, попадет в детектор ((5) на диаграмме) только в одном из двух мест. Согласно теории квантовых измерений , волновая функция, представляющая магнитный момент атома, находится в суперпозиции этих двух направлений, входящих в магнит. Единственное собственное значение в направлении вращения регистрируется, когда квант импульса передается из магнитного поля к атому, вызывая ускорение и смещение в этом направлении импульса. ^[26]

См. также

Ссылки

^ Перейти обратно: ^а ^б ^с Герлах, В.; Стерн, О. (1922). «Экспериментальное подтверждение направленного квантования в магнитном поле». Журнал физики . 9 (1): 349–352. Бибкод : 1922ZPhy....9..349G . дои : 10.1007/BF01326983 . S2CID 186228677 .
^ Аллан Франклин; Слободан Перович. «Опыт по физике, Приложение 5» . В Эдварде Н. Залте (ред.). Стэнфордская энциклопедия философии (изд. Зима 2016 г.) . Проверено 14 августа 2018 г.
^ Фридрих, Б.; Хершбах, Д. (2003). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику» . Физика сегодня . 56 (12): 53. Бибкод : 2003ФТ....56л..53Ф . дои : 10.1063/1.1650229 . S2CID 17572089 .
^ Кастельвекки, Д. (2022). «Эксперимент Штерна-Герлаха на 100» . Обзоры природы Физика . 4 (3): 140–142. Бибкод : 2022НатРП...4..140С . дои : 10.1038/s42254-022-00436-4 . S2CID 247184330 .
^ Герлах, В.; Стерн, О. (1922). «Магнитный момент атома серебра». Журнал физики . 9 (1): 353–355. Бибкод : 1922ZPhy....9..353G . дои : 10.1007/BF01326984 . S2CID 126109346 .
^ Герлах, В.; Стерн, О. (1922). «Экспериментальное подтверждение магнитного момента атома серебра» . Журнал физики . 8 (1): 110–111. Бибкод : 1922ZPhy....8..110G . дои : 10.1007/BF01329580 . S2CID 122648402 .
^ Мотт, Н.Ф. , Мэсси, HSW (1965/1971). Теория атомных столкновений , третье издание, Oxford University Press, Oxford UK, стр. 214–219, §2, гл. IX, перепечатано в Уилер, Дж.А. ; Журек, WH (1983). Квантовая теория и измерения . Принстон, штат Нью-Джерси: Издательство Принстонского университета. стр. 701–706.
^ Джордж Х. Резерфорд и Райнер Гроуб (1997). «Комментарий к статье «Эффект Штерна-Герлаха для электронных пучков» ». Физ. Преподобный Летт . 81 (4772): 4772. Бибкод : 1998PhRvL..81.4772R . doi : 10.1103/PhysRevLett.81.4772 .
^ Перейти обратно: ^а ^б Сакураи, Ж.-Ж. (1985). Современная квантовая механика . Аддисон-Уэсли . ISBN 0-201-53929-2 .
^ Перейти обратно: ^а ^б ^с Циньсюнь, Ли (8 июня 2020 г.). «Эксперимент Штерна Герлаха: описания и разработки» . Университет науки и технологий Китая : 2–5 . Проверено 24 ноября 2020 г.
^ Кастельвекки, Давиде (2020). "Момент". Физика природы . 16 (9): 994. Бибкод : 2020NatPh..16..994C . дои : 10.1038/s41567-020-1022-6 . S2CID 225215678 .
^ Краг, Хельге (2012). «Теория Бора – Зоммерфельда». Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925 гг . Издательство Оксфордского университета. стр. 140–181. doi : 10.1093/acprof:oso/9780199654987.003.0004 . ISBN 978-0-19-965498-7 .
^ Стерн, О. (1921). «Способ экспериментальной проверки направленного квантования в магнитном поле». Журнал физики . 7 (1): 249–253. Бибкод : 1921ZPhy....7..249S . дои : 10.1007/BF01332793 . S2CID 186234469 .
^ Френч, AP , Тейлор, EF (1979). Введение в квантовую физику , Ван Ностранд Рейнхольд, Лондон, ISBN 0-442-30770-5 , стр. 428–442.
^ Айсберг, Роберт; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Уайли. п. 277. ИСБН 9780471873730 .
^ Вайнерт, Ф. (1995). «Неправильная теория — правильный эксперимент: значение экспериментов Штерна-Герлаха». Исследования по истории и философии современной физики . 26Б (1): 75–86. Бибкод : 1995ШПМП..26...75Вт . дои : 10.1016/1355-2198(95)00002-Б .
^ Фиппс, TE; Тейлор, Дж. Б. (1927). «Магнитный момент атома водорода». Физический обзор . 29 (2): 309–320. Бибкод : 1927PhRv...29..309P . дои : 10.1103/PhysRev.29.309 .
^ Келлог, JBM; Миллман, С. (1 июля 1946 г.). «Метод молекулярно-лучевого магнитного резонанса. Радиочастотные спектры атомов и молекул» . Обзоры современной физики . 18 (3): 323–352. дои : 10.1103/RevModPhys.18.323 . ISSN 0034-6861 .
^ Раби, II; Захариас-младший; Миллман С. и Куш П. (1938). «Новый метод измерения ядерного магнитного момента» . Физический обзор . 53 (4): 318–327. Бибкод : 1938PhRv...53..318R . дои : 10.1103/PhysRev.53.318 .
^ Гамильтон, Дональд Р. (1 декабря 1941 г.). «Молекулярные пучки и ядерные моменты» . Американский журнал физики . 9 (6): 319–337. дои : 10.1119/1.1991712 . ISSN 0002-9505 .
^ «Нобелевская премия по физике 1944 года» . NobelPrize.org .
^ Гриффитс, Дэвид (2005). Введение в квантовую механику, 2-е изд . Пирсон Прентис Холл . п. 267. ИСБН 0-13-111892-7 .
^ Бом, Дэвид (1951). Квантовая теория . Нью-Йорк: Прентис-Холл. стр. 326–330.
^ Готфрид, Курт (1966). Квантовая механика . Нью-Йорк: WA Benjamin, Inc., стр. 170–174.
^ Айсберг, Роберт (1961). Основы современной физики . Нью-Йорк: Джон Уайли и сыновья. стр. 334–338. ISBN 0-471-23463-Х .
^ Деверо, Майкл (2015). «Редукция волновой функции атома в магнитном поле Штерна – Герлаха». Канадский физический журнал . 93 (11): 1382–1390. Бибкод : 2015CaJPh..93.1382D . дои : 10.1139/cjp-2015-0031 . hdl : 1807/69186 . ISSN 0008-4204 .

Дальнейшее чтение

Деверо, М. (2015). «Редукция волновой функции атома в магнитном поле Штерна-Герлаха». Канадский физический журнал . 93 (11): 1382–1390. Бибкод : 2015CaJPh..93.1382D . дои : 10.1139/cjp-2015-0031 . hdl : 1807/69186 .
Майкл Деверо - Редукция волновой функции атома в магнитном поле Штерна-Герлаха
Фридрих, Б.; Хершбах, Д. (2003). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику» . Физика сегодня . 56 (12): 53. Бибкод : 2003ФТ....56л..53Ф . дои : 10.1063/1.1650229 . S2CID 17572089 .
Райниш, Г. (1999). «Эксперимент Штерна-Герлаха как пионерский и, вероятно, самый простой тест квантовой запутанности?». Буквы по физике А. 259 (6): 427–430. Бибкод : 1999PhLA..259..427R . дои : 10.1016/S0375-9601(99)00472-7 .
Венугопалан, А. (1997). «Декогеренция и состояния кота Шредингера в эксперименте типа Штерна-Герлаха». Физический обзор А. 56 (5): 4307–4310. Бибкод : 1997PhRvA..56.4307V . дои : 10.1103/PhysRevA.56.4307 .
Сюй, Б.; Беррондо, М.; Ван Хюле, Ж.-Ф. (2011). «Динамика Штерна-Герлаха с квантовыми пропагаторами» . Физический обзор А. 83 (1): 012109–1–12. Бибкод : 2011PhRvA..83a2109H . дои : 10.1103/PhysRevA.83.012109 .
Джереми Бернштейн (2010). «Эксперимент Штерна Герлаха». arXiv : 1007.2435v1 [ physical.hist-ph ].
(Часто) упускаемый из виду эксперимент, открывший квантовый мир

Внешние ссылки

[SG-1] Перейти обратно: ^а ^б ^с Герлах, В.; Стерн, О. (1922). «Экспериментальное подтверждение направленного квантования в магнитном поле». Журнал физики . 9 (1): 349–352. Бибкод : 1922ZPhy....9..349G . дои : 10.1007/BF01326983 . S2CID 186228677 .

[2] Аллан Франклин; Слободан Перович. «Опыт по физике, Приложение 5» . В Эдварде Н. Залте (ред.). Стэнфордская энциклопедия философии (изд. Зима 2016 г.) . Проверено 14 августа 2018 г.

[FH2003-3] Фридрих, Б.; Хершбах, Д. (2003). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику» . Физика сегодня . 56 (12): 53. Бибкод : 2003ФТ....56л..53Ф . дои : 10.1063/1.1650229 . S2CID 17572089 .

[4] Кастельвекки, Д. (2022). «Эксперимент Штерна-Герлаха на 100» . Обзоры природы Физика . 4 (3): 140–142. Бибкод : 2022НатРП...4..140С . дои : 10.1038/s42254-022-00436-4 . S2CID 247184330 .

[5] Герлах, В.; Стерн, О. (1922). «Магнитный момент атома серебра». Журнал физики . 9 (1): 353–355. Бибкод : 1922ZPhy....9..353G . дои : 10.1007/BF01326984 . S2CID 126109346 .

[6] Герлах, В.; Стерн, О. (1922). «Экспериментальное подтверждение магнитного момента атома серебра» . Журнал физики . 8 (1): 110–111. Бибкод : 1922ZPhy....8..110G . дои : 10.1007/BF01329580 . S2CID 122648402 .

[7] Мотт, Н.Ф. , Мэсси, HSW (1965/1971). Теория атомных столкновений , третье издание, Oxford University Press, Oxford UK, стр. 214–219, §2, гл. IX, перепечатано в Уилер, Дж.А. ; Журек, WH (1983). Квантовая теория и измерения . Принстон, штат Нью-Джерси: Издательство Принстонского университета. стр. 701–706.

[8] Джордж Х. Резерфорд и Райнер Гроуб (1997). «Комментарий к статье «Эффект Штерна-Герлаха для электронных пучков» ». Физ. Преподобный Летт . 81 (4772): 4772. Бибкод : 1998PhRvL..81.4772R . doi : 10.1103/PhysRevLett.81.4772 .

[Sakurai1985-9] Перейти обратно: ^а ^б Сакураи, Ж.-Ж. (1985). Современная квантовая механика . Аддисон-Уэсли . ISBN 0-201-53929-2 .

[:0-10] Перейти обратно: ^а ^б ^с Циньсюнь, Ли (8 июня 2020 г.). «Эксперимент Штерна Герлаха: описания и разработки» . Университет науки и технологий Китая : 2–5 . Проверено 24 ноября 2020 г.

[11] Кастельвекки, Давиде (2020). "Момент". Физика природы . 16 (9): 994. Бибкод : 2020NatPh..16..994C . дои : 10.1038/s41567-020-1022-6 . S2CID 225215678 .

[12] Краг, Хельге (2012). «Теория Бора – Зоммерфельда». Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925 гг . Издательство Оксфордского университета. стр. 140–181. doi : 10.1093/acprof:oso/9780199654987.003.0004 . ISBN 978-0-19-965498-7 .

[13] Стерн, О. (1921). «Способ экспериментальной проверки направленного квантования в магнитном поле». Журнал физики . 7 (1): 249–253. Бибкод : 1921ZPhy....7..249S . дои : 10.1007/BF01332793 . S2CID 186234469 .

[14] Френч, AP , Тейлор, EF (1979). Введение в квантовую физику , Ван Ностранд Рейнхольд, Лондон, ISBN 0-442-30770-5 , стр. 428–442.

[15] Айсберг, Роберт; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Уайли. п. 277. ИСБН 9780471873730 .

[16] Вайнерт, Ф. (1995). «Неправильная теория — правильный эксперимент: значение экспериментов Штерна-Герлаха». Исследования по истории и философии современной физики . 26Б (1): 75–86. Бибкод : 1995ШПМП..26...75Вт . дои : 10.1016/1355-2198(95)00002-Б .

[17] Фиппс, TE; Тейлор, Дж. Б. (1927). «Магнитный момент атома водорода». Физический обзор . 29 (2): 309–320. Бибкод : 1927PhRv...29..309P . дои : 10.1103/PhysRev.29.309 .

[KelloggMillman-18] Келлог, JBM; Миллман, С. (1 июля 1946 г.). «Метод молекулярно-лучевого магнитного резонанса. Радиочастотные спектры атомов и молекул» . Обзоры современной физики . 18 (3): 323–352. дои : 10.1103/RevModPhys.18.323 . ISSN 0034-6861 .

[19] Раби, II; Захариас-младший; Миллман С. и Куш П. (1938). «Новый метод измерения ядерного магнитного момента» . Физический обзор . 53 (4): 318–327. Бибкод : 1938PhRv...53..318R . дои : 10.1103/PhysRev.53.318 .

[20] Гамильтон, Дональд Р. (1 декабря 1941 г.). «Молекулярные пучки и ядерные моменты» . Американский журнал физики . 9 (6): 319–337. дои : 10.1119/1.1991712 . ISSN 0002-9505 .

[21] «Нобелевская премия по физике 1944 года» . NobelPrize.org .

[22] Гриффитс, Дэвид (2005). Введение в квантовую механику, 2-е изд . Пирсон Прентис Холл . п. 267. ИСБН 0-13-111892-7 .

[23] Бом, Дэвид (1951). Квантовая теория . Нью-Йорк: Прентис-Холл. стр. 326–330.

[24] Готфрид, Курт (1966). Квантовая механика . Нью-Йорк: WA Benjamin, Inc., стр. 170–174.

[25] Айсберг, Роберт (1961). Основы современной физики . Нью-Йорк: Джон Уайли и сыновья. стр. 334–338. ISBN 0-471-23463-Х .

[26] Деверо, Майкл (2015). «Редукция волновой функции атома в магнитном поле Штерна – Герлаха». Канадский физический журнал . 93 (11): 1382–1390. Бибкод : 2015CaJPh..93.1382D . дои : 10.1139/cjp-2015-0031 . hdl : 1807/69186 . ISSN 0008-4204 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

v т и Квантовая механика
Background	Introduction History Timeline Classical mechanics Old quantum theory Glossary
Fundamentals	Born rule Bra–ket notation Complementarity Density matrix Energy level Ground state Excited state Degenerate levels Zero-point energy Entanglement Hamiltonian Interference Decoherence Measurement Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Collapse Wave–particle duality
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective collapse Quantum logic Relational Transactional Von Neumann–Wigner
Experiments	Bell test Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz Mach–Zehnder interferometer Elitzur–Vaidman Popper Quantum eraser Stern–Gerlach Wheeler's delayed choice
Science	Quantum biology Quantum chemistry Quantum chaos Quantum cosmology Quantum differential calculus Quantum dynamics Quantum geometry Quantum measurement problem Quantum mind Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum bus Quantum cellular automata Quantum finite automata Quantum channel Quantum circuit Quantum complexity theory Quantum computing Timeline Quantum cryptography Quantum electronics Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum logic Quantum logic gates Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensing Quantum simulator Quantum teleportation
Extensions	Quantum fluctuation Casimir effect Quantum statistical mechanics Quantum field theory History Quantum gravity Relativistic quantum mechanics
Related	Schrödinger's cat in popular culture Wigner's friend EPR paradox Quantum mysticism
Category