Mathematical functions
Лемнискатный синус (красный) и лемнискатный косинус (фиолетовый) применяются к вещественному аргументу по сравнению с тригонометрическим синусом y = sin( πx / ϖ ) В математике лемнискатные эллиптические функции — это эллиптические функции, связанные с длиной дуги лемнискаты Бернулли . Впервые они были изучены Джулио Фаньяно в 1718 году, а затем, среди других, Леонардом Эйлером и Карлом Фридрихом Гауссом . [ 1 ]
Функции лемниската синус и лемниската косинус , обычно обозначаемые символами sl и cl символы sinlem и coslem или sin lemn и cos lemn ), (иногда вместо них используются [ 2 ] тригонометрическим функциям синус и косинус. В то время как тригонометрический синус связывает длину дуги с длиной хорды в единичного диаметра . круге
x
2
+
y
2
=
x
,
{\displaystyle x^{2}+y^{2}=x,}
[ 3 ]
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
Лемнискатные функции имеют периоды, связанные с числом.
ϖ
=
{\displaystyle \varpi =}
константой лемнискаты и представляет собой отношение периметра лемнискаты к ее диаметру. Это число является четвертой степени . аналогом ( квадратичного )
π
=
{\displaystyle \pi =}
отношение периметра к диаметру круга .
Как комплексные функции , sl и cl имеют квадратную решетку периодов (кратных гауссовским целым числам ) с фундаментальными периодами.
{
(
1
+
i
)
ϖ
,
(
1
−
i
)
ϖ
}
,
{\displaystyle \{(1+i)\varpi ,(1-i)\varpi \},}
[ 4 ] эллиптических функций Якоби на этой решетке:
sl
z
=
sn
(
z
;
i
)
,
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;i),}
cl
z
=
cd
(
z
;
i
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;i)}
Точно так же гиперболическая лемниската sine slh и гиперболическая лемниската cosine clh имеют квадратную решетку периодов с фундаментальными периодами.
{
2
ϖ
,
2
ϖ
i
}
.
{\displaystyle {\bigl \{}{\sqrt {2}}\varpi ,{\sqrt {2}}\varpi i{\bigr \}}.}
Функции лемнискаты и гиперболические функции лемнискаты связаны с эллиптической функцией Вейерштрасса.
℘
(
z
;
a
,
0
)
{\displaystyle \wp (z;a,0)}
Функции лемнискаты sl и cl можно определить как решение проблемы начального значения : [ 5 ]
d
d
z
sl
z
=
(
1
+
sl
2
z
)
cl
z
,
d
d
z
cl
z
=
−
(
1
+
cl
2
z
)
sl
z
,
sl
0
=
0
,
cl
0
=
1
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z={\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}\operatorname {cl} z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=-{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}\operatorname {sl} z,\ \operatorname {sl} 0=0,\ \operatorname {cl} 0=1,}
или, что то же самое, как обратный эллиптический интеграл , отображение Шварца – Кристоффеля из комплексного единичного диска в квадрат с углами.
{
1
2
ϖ
,
1
2
ϖ
i
,
−
1
2
ϖ
,
−
1
2
ϖ
i
}
:
{\displaystyle {\big \{}{\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi i,-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi i{\big \}}\colon }
[ 6 ]
z
=
∫
0
sl
z
d
t
1
−
t
4
=
∫
cl
z
1
d
t
1
−
t
4
.
{\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
За пределами этого квадрата функции можно аналитически продолжить на всю комплексную плоскость с помощью серии отражений .
Для сравнения, круговой синус и косинус можно определить как решение задачи начального значения:
d
d
z
sin
z
=
cos
z
,
d
d
z
cos
z
=
−
sin
z
,
sin
0
=
0
,
cos
0
=
1
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\sin z=\cos z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\cos z=-\sin z,\ \sin 0=0,\ \cos 0=1,}
или как инверсию отображения верхней полуплоскости в полубесконечную полосу с вещественной частью между
−
1
2
π
,
1
2
π
{\displaystyle -{\tfrac {1}{2}}\pi ,{\tfrac {1}{2}}\pi }
z
=
∫
0
sin
z
d
t
1
−
t
2
=
∫
cos
z
1
d
t
1
−
t
2
.
{\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}.}
Функция лемнискатного синуса и гиперболические функции лемнискатного синуса определяются как обратные эллиптическим интегралам. Полные интегралы связаны с константой лемнискаты ϖ . Функции лемнискат имеют минимальный действительный период 2 ϖ , минимальный мнимый период 2 ϖ i и фундаментальные комплексные периоды.
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
ϖ, константой лемнискаты [ 7 ]
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2.62205
…
{\displaystyle \varpi =2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=2.62205\ldots }
Лемнискатные функции удовлетворяют основному соотношению
cl
z
=
sl
(
1
2
ϖ
−
z
)
,
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )},}
cos
z
=
sin
(
1
2
π
−
z
)
.
{\displaystyle \cos z={\sin }{\bigl (}{\tfrac {1}{2}}\pi -z{\bigr )}.}
Константа лемнискаты ϖ константы круга π , и многие тождества, включающие π, ϖ тригонометрические функции, имеют аналоги, включающие функции лемнискаты. Например, формулу Вьета для π
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
Аналогичная формула для ϖ [ 8 ]
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
{\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
Формула Мачина для π
1
4
π
=
4
arctan
1
5
−
arctan
1
239
,
{\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}
π
1
4
π
=
arctan
1
2
+
arctan
1
3
{\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}
ϖ
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
.
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}.}
[ 9 ]
Гаусс обнаружил, что константы лемнискаты и окружности связаны друг с другом средним арифметико-геометрическим M [ 10 ]
π
ϖ
=
M
(
1
,
2
)
{\displaystyle {\frac {\pi }{\varpi }}=M{\left(1,{\sqrt {2}}\!~\right)}}
sl
{\displaystyle \operatorname {sl} }
[ 11 ]
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
Лемнискатные функции cl и sl — четные и нечетные функции соответственно:
cl
(
−
z
)
=
cl
z
sl
(
−
z
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\[6mu]\operatorname {sl} (-z)&=-\operatorname {sl} z\end{aligned}}}
При переводах
1
2
ϖ
,
{\displaystyle {\tfrac {1}{2}}\varpi ,}
cl и sl меняются местами, а при трансляциях
1
2
i
ϖ
{\displaystyle {\tfrac {1}{2}}i\varpi }
совершают возвратно-поступательные движения : [ 12 ]
cl
(
z
±
1
2
ϖ
)
=
∓
sl
z
,
cl
(
z
±
1
2
i
ϖ
)
=
∓
i
sl
z
sl
(
z
±
1
2
ϖ
)
=
±
cl
z
,
sl
(
z
±
1
2
i
ϖ
)
=
±
i
cl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}
Удвоение этих переводов на единицу - целое число по Гауссу, кратное
ϖ
{\displaystyle \varpi }
±
ϖ
{\displaystyle \pm \varpi }
±
i
ϖ
{\displaystyle \pm i\varpi }
инволюцию :
cl
(
z
+
ϖ
)
=
cl
(
z
+
i
ϖ
)
=
−
cl
z
sl
(
z
+
ϖ
)
=
sl
(
z
+
i
ϖ
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+i\varpi )=-\operatorname {cl} z\\[4mu]\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{aligned}}}
В результате обе функции инвариантны относительно перевода на четное целое число Гаусса, кратное
ϖ
{\displaystyle \varpi }
[ 13 ]
(
a
+
b
i
)
ϖ
,
{\displaystyle (a+bi)\varpi ,}
a
+
b
=
2
k
{\displaystyle a+b=2k}
a b k
cl
(
z
+
(
1
+
i
)
ϖ
)
=
cl
(
z
+
(
1
−
i
)
ϖ
)
=
cl
z
sl
(
z
+
(
1
+
i
)
ϖ
)
=
sl
(
z
+
(
1
−
i
)
ϖ
)
=
sl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\end{aligned}}}
Это делает их эллиптическими функциями (двоякопериодическими мероморфными функциями в комплексной плоскости) с диагональной квадратной решеткой периодов фундаментальных периодов.
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
[ 14 ]
Отражения и повороты на четверть оборота аргументов функции лемнискаты имеют простые выражения:
cl
z
¯
=
cl
z
¯
sl
z
¯
=
sl
z
¯
cl
i
z
=
1
cl
z
sl
i
z
=
i
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}
Функция sl имеет простые нули в гауссовских целых кратных ϖ
a
ϖ
+
b
ϖ
i
{\displaystyle a\varpi +b\varpi i}
a b полюса в гауссовых полуцелых кратных ϖ
(
a
+
1
2
)
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i}
остатками
(
−
1
)
a
−
b
+
1
i
{\displaystyle (-1)^{a-b+1}i}
cl отражается и смещается от функции sl ,
cl
z
=
sl
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}}
(
a
+
1
2
)
ϖ
+
b
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +b\varpi i}
a
ϖ
+
(
b
+
1
2
)
ϖ
i
,
{\displaystyle a\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i,}
(
−
1
)
a
−
b
i
.
{\displaystyle (-1)^{a-b}i.}
Также
sl
z
=
sl
w
↔
z
=
(
−
1
)
m
+
n
w
+
(
m
+
n
i
)
ϖ
{\displaystyle \operatorname {sl} z=\operatorname {sl} w\leftrightarrow z=(-1)^{m+n}w+(m+ni)\varpi }
для некоторых
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
sl
(
(
1
±
i
)
z
)
=
(
1
±
i
)
sl
z
sl
′
z
.
{\displaystyle \operatorname {sl} ((1\pm i)z)=(1\pm i){\frac {\operatorname {sl} z}{\operatorname {sl} 'z}}.}
Последняя формула представляет собой частный случай комплексного умножения . Аналогичные формулы можно привести для
sl
(
(
n
+
m
i
)
z
)
{\displaystyle \operatorname {sl} ((n+mi)z)}
n
+
m
i
{\displaystyle n+mi}
sl
{\displaystyle \operatorname {sl} }
Z
[
i
]
{\displaystyle \mathbb {Z} [i]}
[ 15 ]
Существуют также бесконечные ряды, отражающие распределение нулей и полюсов sl : [ 16 ] [ 17 ]
1
sl
z
=
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
n
ϖ
+
k
ϖ
i
{\displaystyle {\frac {1}{\operatorname {sl} z}}=\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+n\varpi +k\varpi i}}}
sl
z
=
−
i
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
(
n
+
1
/
2
)
ϖ
+
(
k
+
1
/
2
)
ϖ
i
.
{\displaystyle \operatorname {sl} z=-i\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+(n+1/2)\varpi +(k+1/2)\varpi i}}.}
Кривые x² ⊕ y² = a a . Отрицательный a a a = ±1 a = ∞ Функции лемнискаты удовлетворяют пифагорейскому тождеству:
c
l
2
z
+
s
l
2
z
+
c
l
2
z
s
l
2
z
=
1
{\displaystyle \operatorname {cl^{2}} z+\operatorname {sl^{2}} z+\operatorname {cl^{2}} z\,\operatorname {sl^{2}} z=1}
В результате параметрическое уравнение
(
x
,
y
)
=
(
cl
t
,
sl
t
)
{\displaystyle (x,y)=(\operatorname {cl} t,\operatorname {sl} t)}
кривую четвертой степени
x
2
+
y
2
+
x
2
y
2
=
1.
{\displaystyle x^{2}+y^{2}+x^{2}y^{2}=1.}
Это тождество можно альтернативно переписать: [ 18 ]
(
1
+
c
l
2
z
)
(
1
+
s
l
2
z
)
=
2
{\displaystyle {\bigl (}1+\operatorname {cl^{2}} z{\bigr )}{\bigl (}1+\operatorname {sl^{2}} z{\bigr )}=2}
c
l
2
z
=
1
−
s
l
2
z
1
+
s
l
2
z
,
s
l
2
z
=
1
−
c
l
2
z
1
+
c
l
2
z
{\displaystyle \operatorname {cl^{2}} z={\frac {1-\operatorname {sl^{2}} z}{1+\operatorname {sl^{2}} z}},\quad \operatorname {sl^{2}} z={\frac {1-\operatorname {cl^{2}} z}{1+\operatorname {cl^{2}} z}}}
Определение оператора касательной суммы как
a
⊕
b
:=
tan
(
arctan
a
+
arctan
b
)
=
a
+
b
1
−
a
b
,
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b)={\frac {a+b}{1-ab}},}
c
l
2
z
⊕
s
l
2
z
=
1.
{\displaystyle \operatorname {cl^{2}} z\oplus \operatorname {sl^{2}} z=1.}
Функции
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
(
∫
0
x
cl
~
t
d
t
)
2
+
(
1
−
∫
0
x
sl
~
t
d
t
)
2
=
1.
{\displaystyle \left(\int _{0}^{x}{\tilde {\operatorname {cl} }}\,t\,\mathrm {d} t\right)^{2}+\left(1-\int _{0}^{x}{\tilde {\operatorname {sl} }}\,t\,\mathrm {d} t\right)^{2}=1.}
Производные следующие:
d
d
z
cl
z
=
c
l
′
z
=
−
(
1
+
c
l
2
z
)
sl
z
=
−
2
sl
z
sl
2
z
+
1
c
l
′
2
z
=
1
−
c
l
4
z
d
d
z
sl
z
=
s
l
′
z
=
(
1
+
s
l
2
z
)
cl
z
=
2
cl
z
cl
2
z
+
1
s
l
′
2
z
=
1
−
s
l
4
z
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-{\bigl (}1+\operatorname {cl^{2}} z{\bigr )}\operatorname {sl} z=-{\frac {2\operatorname {sl} z}{\operatorname {sl} ^{2}z+1}}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&={\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\operatorname {cl} z={\frac {2\operatorname {cl} z}{\operatorname {cl} ^{2}z+1}}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}
d
d
z
cl
~
z
=
−
2
sl
~
z
cl
z
−
sl
~
z
cl
z
d
d
z
sl
~
z
=
2
cl
~
z
cl
z
−
cl
~
z
cl
z
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\,{\tilde {\operatorname {cl} }}\,z&=-2\,{\tilde {\operatorname {sl} }}\,z\,\operatorname {cl} z-{\frac {{\tilde {\operatorname {sl} }}\,z}{\operatorname {cl} z}}\\{\frac {\mathrm {d} }{\mathrm {d} z}}\,{\tilde {\operatorname {sl} }}\,z&=2\,{\tilde {\operatorname {cl} }}\,z\,\operatorname {cl} z-{\frac {{\tilde {\operatorname {cl} }}\,z}{\operatorname {cl} z}}\end{aligned}}}
Вторые производные лемнискатного синуса и лемнискатного косинуса представляют собой их отрицательные дублированные кубы:
d
2
d
z
2
cl
z
=
−
2
c
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {cl} z=-2\operatorname {cl^{3}} z}
d
2
d
z
2
sl
z
=
−
2
s
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {sl} z=-2\operatorname {sl^{3}} z}
Функции лемнискаты можно интегрировать с помощью функции обратного тангенса:
∫
cl
z
d
z
=
arctan
sl
z
+
C
∫
sl
z
d
z
=
−
arctan
cl
z
+
C
∫
cl
~
z
d
z
=
sl
~
z
cl
z
+
C
∫
sl
~
z
d
z
=
−
cl
~
z
cl
z
+
C
{\displaystyle {\begin{aligned}\int \operatorname {cl} z\mathop {\mathrm {d} z} &=\arctan \operatorname {sl} z+C\\\int \operatorname {sl} z\mathop {\mathrm {d} z} &=-\arctan \operatorname {cl} z+C\\\int {\tilde {\operatorname {cl} }}\,z\,\mathrm {d} z&={\frac {{\tilde {\operatorname {sl} }}\,z}{\operatorname {cl} z}}+C\\\int {\tilde {\operatorname {sl} }}\,z\,\mathrm {d} z&=-{\frac {{\tilde {\operatorname {cl} }}\,z}{\operatorname {cl} z}}+C\end{aligned}}}
Подобно тригонометрическим функциям, лемнискатные функции удовлетворяют тождествам суммы аргументов и разностей. Первоначальное обозначение, использованное Фаньяно для разделения лемнискаты пополам, было: [ 19 ]
sl
(
u
+
v
)
=
sl
u
s
l
′
v
+
sl
v
s
l
′
u
1
+
s
l
2
u
s
l
2
v
{\displaystyle \operatorname {sl} (u+v)={\frac {\operatorname {sl} u\,\operatorname {sl'} v+\operatorname {sl} v\,\operatorname {sl'} u}{1+\operatorname {sl^{2}} u\,\operatorname {sl^{2}} v}}}
Производные и пифагорейские тождества могут быть использованы для переработки тождества, используемого Фагано, в терминах sl и cl . Определение касательной суммы оператора
a
⊕
b
:=
tan
(
arctan
a
+
arctan
b
)
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b)}
a
⊖
b
:=
a
⊕
(
−
b
)
,
{\displaystyle a\ominus b\mathrel {:=} a\oplus (-b),}
[ 20 ]
cl
(
u
+
v
)
=
cl
u
cl
v
⊖
sl
u
sl
v
=
cl
u
cl
v
−
sl
u
sl
v
1
+
sl
u
cl
u
sl
v
cl
v
cl
(
u
−
v
)
=
cl
u
cl
v
⊕
sl
u
sl
v
sl
(
u
+
v
)
=
sl
u
cl
v
⊕
cl
u
sl
v
=
sl
u
cl
v
+
cl
u
sl
v
1
−
sl
u
cl
u
sl
v
cl
v
sl
(
u
−
v
)
=
sl
u
cl
v
⊖
cl
u
sl
v
{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}
Они напоминают свои тригонометрические аналоги :
cos
(
u
±
v
)
=
cos
u
cos
v
∓
sin
u
sin
v
sin
(
u
±
v
)
=
sin
u
cos
v
±
cos
u
sin
v
{\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v)&=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}
В частности, для вычисления комплекснозначных функций в реальных компонентах,
cl
(
x
+
i
y
)
=
cl
x
−
i
sl
x
sl
y
cl
y
cl
y
+
i
sl
x
cl
x
sl
y
=
cl
x
cl
y
(
1
−
sl
2
x
sl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
−
i
sl
x
sl
y
(
cl
2
x
+
cl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
sl
(
x
+
i
y
)
=
sl
x
+
i
cl
x
sl
y
cl
y
cl
y
−
i
sl
x
cl
x
sl
y
=
sl
x
cl
y
(
1
−
cl
2
x
sl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
+
i
cl
x
sl
y
(
sl
2
x
+
cl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
{\displaystyle {\begin{aligned}\operatorname {cl} (x+iy)&={\frac {\operatorname {cl} x-i\operatorname {sl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y+i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {cl} x\,\operatorname {cl} y\left(1-\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}-i{\frac {\operatorname {sl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\\[12mu]\operatorname {sl} (x+iy)&={\frac {\operatorname {sl} x+i\operatorname {cl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y-i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {sl} x\,\operatorname {cl} y\left(1-\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}+i{\frac {\operatorname {cl} x\,\operatorname {sl} y\left(\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\end{aligned}}}
Формулы биссектрисы:
cl
2
1
2
x
=
1
+
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
{\displaystyle \operatorname {cl} ^{2}{\tfrac {1}{2}}x={\frac {1+\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}}}
sl
2
1
2
x
=
1
−
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
{\displaystyle \operatorname {sl} ^{2}{\tfrac {1}{2}}x={\frac {1-\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}}}
Формулы дублирования: [ 21 ]
cl
2
x
=
−
1
+
2
cl
2
x
+
cl
4
x
1
+
2
cl
2
x
−
cl
4
x
{\displaystyle \operatorname {cl} 2x={\frac {-1+2\,\operatorname {cl} ^{2}x+\operatorname {cl} ^{4}x}{1+2\,\operatorname {cl} ^{2}x-\operatorname {cl} ^{4}x}}}
sl
2
x
=
2
sl
x
cl
x
1
+
sl
2
x
1
+
sl
4
x
{\displaystyle \operatorname {sl} 2x=2\,\operatorname {sl} x\,\operatorname {cl} x{\frac {1+\operatorname {sl} ^{2}x}{1+\operatorname {sl} ^{4}x}}}
Формулы трипликации: [ 21 ]
cl
3
x
=
−
3
cl
x
+
6
cl
5
x
+
cl
9
x
1
+
6
cl
4
x
−
3
cl
8
x
{\displaystyle \operatorname {cl} 3x={\frac {-3\,\operatorname {cl} x+6\,\operatorname {cl} ^{5}x+\operatorname {cl} ^{9}x}{1+6\,\operatorname {cl} ^{4}x-3\,\operatorname {cl} ^{8}x}}}
sl
3
x
=
3
sl
x
−
6
sl
5
x
−
1
sl
9
x
1
+
6
sl
4
x
−
3
sl
8
x
{\displaystyle \operatorname {sl} 3x={\frac {\color {red}{3}\,\color {black}{\operatorname {sl} x-\,}\color {green}{6}\,\color {black}{\operatorname {sl} ^{5}x-\,}\color {blue}{1}\,\color {black}{\operatorname {sl} ^{9}x}}{\color {blue}{1}\,\color {black}{+\,}\,\color {green}{6}\,\color {black}{\operatorname {sl} ^{4}x-\,}\color {red}{3}\,\color {black}{\operatorname {sl} ^{8}x}}}}
Обратите внимание на «обратную симметрию» коэффициентов числителя и знаменателя
sl
3
x
{\displaystyle \operatorname {sl} 3x}
sl
β
x
{\displaystyle \operatorname {sl} \beta x}
β
=
m
+
n
i
{\displaystyle \beta =m+ni}
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
[ 15 ]
Позволять
L
{\displaystyle L}
решеткой
L
=
Z
(
1
+
i
)
ϖ
+
Z
(
1
−
i
)
ϖ
.
{\displaystyle L=\mathbb {Z} (1+i)\varpi +\mathbb {Z} (1-i)\varpi .}
Кроме того, пусть
K
=
Q
(
i
)
{\displaystyle K=\mathbb {Q} (i)}
O
=
Z
[
i
]
{\displaystyle {\mathcal {O}}=\mathbb {Z} [i]}
z
∈
C
{\displaystyle z\in \mathbb {C} }
β
=
m
+
i
n
{\displaystyle \beta =m+in}
γ
=
m
′
+
i
n
′
{\displaystyle \gamma =m'+in'}
m
,
n
,
m
′
,
n
′
∈
Z
{\displaystyle m,n,m',n'\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
m
′
+
n
′
{\displaystyle m'+n'}
γ
≡
1
mod
2
(
1
+
i
)
{\displaystyle \gamma \equiv 1\,\operatorname {mod} \,2(1+i)}
sl
β
z
=
M
β
(
sl
z
)
{\displaystyle \operatorname {sl} \beta z=M_{\beta }(\operatorname {sl} z)}
M
β
(
x
)
=
i
ε
x
P
β
(
x
4
)
Q
β
(
x
4
)
{\displaystyle M_{\beta }(x)=i^{\varepsilon }x{\frac {P_{\beta }(x^{4})}{Q_{\beta }(x^{4})}}}
для некоторых взаимно простых многочленов
P
β
(
x
)
,
Q
β
(
x
)
∈
O
[
x
]
{\displaystyle P_{\beta }(x),Q_{\beta }(x)\in {\mathcal {O}}[x]}
ε
∈
{
0
,
1
,
2
,
3
}
{\displaystyle \varepsilon \in \{0,1,2,3\}}
[ 22 ]
x
P
β
(
x
4
)
=
∏
γ
|
β
Λ
γ
(
x
)
{\displaystyle xP_{\beta }(x^{4})=\prod _{\gamma |\beta }\Lambda _{\gamma }(x)}
и
Λ
β
(
x
)
=
∏
[
α
]
∈
(
O
/
β
O
)
×
(
x
−
sl
α
δ
β
)
{\displaystyle \Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta })}
где
δ
β
{\displaystyle \delta _{\beta }}
β
{\displaystyle \beta }
торсионный генератор (т.е.
δ
β
∈
(
1
/
β
)
L
{\displaystyle \delta _{\beta }\in (1/\beta )L}
[
δ
β
]
∈
(
1
/
β
)
L
/
L
{\displaystyle [\delta _{\beta }]\in (1/\beta )L/L}
(
1
/
β
)
L
/
L
{\displaystyle (1/\beta )L/L}
O
{\displaystyle {\mathcal {O}}}
модуль ). Примеры
β
{\displaystyle \beta }
2
ϖ
/
β
{\displaystyle 2\varpi /\beta }
(
1
+
i
)
ϖ
/
β
{\displaystyle (1+i)\varpi /\beta }
Λ
β
(
x
)
∈
O
[
x
]
{\displaystyle \Lambda _{\beta }(x)\in {\mathcal {O}}[x]}
β
{\displaystyle \beta }
лемнатомный полином . Оно монично и неприводимо
K
{\displaystyle K}
круговых полиномов . [ 23 ]
Φ
k
(
x
)
=
∏
[
a
]
∈
(
Z
/
k
Z
)
×
(
x
−
ζ
k
a
)
.
{\displaystyle \Phi _{k}(x)=\prod _{[a]\in (\mathbb {Z} /k\mathbb {Z} )^{\times }}(x-\zeta _{k}^{a}).}
The
β
{\displaystyle \beta }
Λ
β
(
x
)
{\displaystyle \Lambda _{\beta }(x)}
минимальным многочленом
sl
δ
β
{\displaystyle \operatorname {sl} \delta _{\beta }}
K
[
x
]
{\displaystyle K[x]}
ω
β
=
sl
(
2
ϖ
/
β
)
{\displaystyle \omega _{\beta }=\operatorname {sl} (2\varpi /\beta )}
ω
~
β
=
sl
(
(
1
+
i
)
ϖ
/
β
)
{\displaystyle {\tilde {\omega }}_{\beta }=\operatorname {sl} ((1+i)\varpi /\beta )}
ω
5
{\displaystyle \omega _{5}}
ω
~
5
{\displaystyle {\tilde {\omega }}_{5}}
K
[
x
]
{\displaystyle K[x]}
Λ
5
(
x
)
=
x
16
+
52
x
12
−
26
x
8
−
12
x
4
+
1
,
{\displaystyle \Lambda _{5}(x)=x^{16}+52x^{12}-26x^{8}-12x^{4}+1,}
и [ 24 ]
ω
5
=
−
13
+
6
5
+
2
85
−
38
5
4
{\displaystyle \omega _{5}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}}}
ω
~
5
=
−
13
−
6
5
+
2
85
+
38
5
4
{\displaystyle {\tilde {\omega }}_{5}={\sqrt[{4}]{-13-6{\sqrt {5}}+2{\sqrt {85+38{\sqrt {5}}}}}}}
[ 25 ] (эквивалентное выражение приведено в таблице ниже). Другой пример: [ 23 ]
Λ
−
1
+
2
i
(
x
)
=
x
4
−
1
+
2
i
{\displaystyle \Lambda _{-1+2i}(x)=x^{4}-1+2i}
который является минимальным полиномом
ω
−
1
+
2
i
{\displaystyle \omega _{-1+2i}}
ω
~
−
1
+
2
i
{\displaystyle {\tilde {\omega }}_{-1+2i}}
K
[
x
]
.
{\displaystyle K[x].}
Если
p
{\displaystyle p}
β
{\displaystyle \beta }
[ 26 ] [ 27 ]
deg
Λ
β
=
β
2
∏
p
|
β
(
1
−
1
p
)
(
1
−
(
−
1
)
(
p
−
1
)
/
2
p
)
{\displaystyle \operatorname {deg} \Lambda _{\beta }=\beta ^{2}\prod _{p|\beta }\left(1-{\frac {1}{p}}\right)\left(1-{\frac {(-1)^{(p-1)/2}}{p}}\right)}
который можно сравнить с круговым аналогом
deg
Φ
k
=
k
∏
p
|
k
(
1
−
1
p
)
.
{\displaystyle \operatorname {deg} \Phi _{k}=k\prod _{p|k}\left(1-{\frac {1}{p}}\right).}
Как и в случае с тригонометрическими функциями, значения функций лемнискаты можно вычислить для разделения лемнискаты на n n
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k целое число , а каждое p i число Ферма . [ 28 ]
n
{\displaystyle n}
cl
n
ϖ
{\displaystyle \operatorname {cl} n\varpi }
sl
n
ϖ
{\displaystyle \operatorname {sl} n\varpi }
1
{\displaystyle 1}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
5
6
{\displaystyle {\tfrac {5}{6}}}
−
2
3
−
3
4
{\displaystyle -{\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
3
4
{\displaystyle {\tfrac {3}{4}}}
−
2
−
1
{\displaystyle -{\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
3
{\displaystyle {\tfrac {2}{3}}}
−
1
2
(
3
+
1
−
12
4
)
{\displaystyle -{\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
{\displaystyle {\tfrac {1}{2}}}
0
{\displaystyle 0}
1
{\displaystyle 1}
1
3
{\displaystyle {\tfrac {1}{3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
4
{\displaystyle {\tfrac {1}{4}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
1
6
{\displaystyle {\tfrac {1}{6}}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
n
{\displaystyle n}
cl
n
ϖ
{\displaystyle \operatorname {cl} n\varpi }
sl
n
ϖ
{\displaystyle \operatorname {sl} n\varpi }
3
7
{\displaystyle {\tfrac {3}{7}}}
tanh
{
1
2
arcoth
[
1
2
2
cos
(
3
14
π
)
cot
(
1
28
π
)
+
cos
(
1
7
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}
5
12
{\displaystyle {\tfrac {5}{12}}}
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
−
1
)
{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}-1{\Bigr )}}
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
+
1
)
{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}+1{\Bigr )}}
2
5
{\displaystyle {\tfrac {2}{5}}}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1){\bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\bigr )}}
2
5
−
2
4
sin
(
3
20
π
)
cos
(
1
20
π
)
{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {3}{20}}\pi )\cos({\tfrac {1}{20}}\pi )}}}
3
8
{\displaystyle {\tfrac {3}{8}}}
(
2
4
−
1
)
(
2
+
1
−
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}
(
2
4
−
1
)
(
2
+
1
+
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}
5
14
{\displaystyle {\tfrac {5}{14}}}
tanh
{
1
2
arcoth
[
1
2
2
sin
(
1
7
π
)
cot
(
3
28
π
)
+
sin
(
1
14
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}\ }
3
10
{\displaystyle {\tfrac {3}{10}}}
2
5
−
2
4
sin
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
1
2
(
5
4
−
1
)
(
5
+
2
+
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\bigr )}}
2
7
{\displaystyle {\tfrac {2}{7}}}
tanh
{
1
2
arcoth
[
1
2
2
cos
(
1
14
π
)
tan
(
5
28
π
)
+
sin
(
3
14
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}\ }
3
14
{\displaystyle {\tfrac {3}{14}}}
tanh
{
1
2
arcoth
[
1
2
2
cos
(
1
14
π
)
tan
(
5
28
π
)
+
sin
(
3
14
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}\ }
1
5
{\displaystyle {\tfrac {1}{5}}}
1
2
(
5
4
−
1
)
(
5
+
2
+
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\bigr )}}
2
5
−
2
4
sin
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
1
7
{\displaystyle {\tfrac {1}{7}}}
tanh
{
1
2
arcoth
[
1
2
2
sin
(
1
7
π
)
cot
(
3
28
π
)
+
sin
(
1
14
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}\ }
1
8
{\displaystyle {\tfrac {1}{8}}}
(
2
4
−
1
)
(
2
+
1
+
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}
(
2
4
−
1
)
(
2
+
1
−
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}
1
10
{\displaystyle {\tfrac {1}{10}}}
2
5
−
2
4
sin
(
3
20
π
)
cos
(
1
20
π
)
{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {3}{20}}\pi )\cos({\tfrac {1}{20}}\pi )}}}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1){\bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\bigr )}}
1
12
{\displaystyle {\tfrac {1}{12}}}
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
+
1
)
{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}+1{\Bigr )}}
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
−
1
)
{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}-1{\Bigr )}}
1
14
{\displaystyle {\tfrac {1}{14}}}
tanh
{
1
2
arcoth
[
1
2
2
cos
(
3
14
π
)
cot
(
1
28
π
)
+
cos
(
1
7
π
)
]
}
{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}
Лемнискатный синус и косинус связывают длину дуги лемнискаты с расстоянием одной конечной точки от начала координат. Тригонометрический синус и косинус аналогичным образом связывают длину дуги окружности единичного диаметра с расстоянием одной конечной точки от начала координат.
L
{\displaystyle {\mathcal {L}}}
лемниската Бернулли с единичным расстоянием от центра до самой дальней точки (т. е. с единичной «полушириной»), важна в теории лемнискатных эллиптических функций. Его можно охарактеризовать как минимум тремя способами:
Угловая характеристика: Учитывая два момента
A
{\displaystyle A}
B
{\displaystyle B}
B
′
{\displaystyle B'}
отражением
B
{\displaystyle B}
A
{\displaystyle A}
L
{\displaystyle {\mathcal {L}}}
замыкание геометрического положения точек
P
{\displaystyle P}
|
A
P
B
−
A
P
B
′
|
{\displaystyle |APB-APB'|}
прямой угол . [ 29 ]
Фокальная характеристика:
L
{\displaystyle {\mathcal {L}}}
F
1
=
(
−
1
2
,
0
)
{\displaystyle F_{1}={\bigl (}{-{\tfrac {1}{\sqrt {2}}}},0{\bigr )}}
F
2
=
(
1
2
,
0
)
{\displaystyle F_{2}={\bigl (}{\tfrac {1}{\sqrt {2}}},0{\bigr )}}
1
2
{\displaystyle {\tfrac {1}{2}}}
Явная координатная характеристика:
L
{\displaystyle {\mathcal {L}}}
кривую четвертой степени, удовлетворяющую полярному уравнению
r
2
=
cos
2
θ
{\displaystyle r^{2}=\cos 2\theta }
декартово уравнение
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
Периметр
L
{\displaystyle {\mathcal {L}}}
2
ϖ
{\displaystyle 2\varpi }
Точки на
L
{\displaystyle {\mathcal {L}}}
r
{\displaystyle r}
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
гипербола
x
2
−
y
2
=
r
4
{\displaystyle x^{2}-y^{2}=r^{4}}
(
x
(
r
)
,
y
(
r
)
)
=
(
1
2
r
2
(
1
+
r
2
)
,
1
2
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}\!{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1+r^{2}{\bigr )}}},\,{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
Используя эту параметризацию с
r
∈
[
0
,
1
]
{\displaystyle r\in [0,1]}
L
{\displaystyle {\mathcal {L}}}
длина дуги от начала координат до точки
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
[ 30 ]
∫
0
r
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
0
r
(
1
+
2
t
2
)
2
2
(
1
+
t
2
)
+
(
1
−
2
t
2
)
2
2
(
1
−
t
2
)
d
t
=
∫
0
r
d
t
1
−
t
4
=
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}
Аналогично, длина дуги от
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
∫
r
1
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
r
1
d
t
1
−
t
4
=
arccl
r
=
1
2
ϖ
−
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\end{aligned}}}
Или в обратном направлении функции лемнискатного синуса и косинуса определяют расстояние от начала координат как функции длины дуги от начала координат и точки.
(
1
,
0
)
{\displaystyle (1,0)}
Аналогично, функции кругового синуса и косинуса связывают длину хорды с длиной дуги для окружности единичного диаметра с помощью полярного уравнения
r
=
cos
θ
{\displaystyle r=\cos \theta }
x
2
+
y
2
=
x
,
{\displaystyle x^{2}+y^{2}=x,}
(
x
(
r
)
,
y
(
r
)
)
=
(
r
2
,
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}r^{2},\,{\sqrt {r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
Альтернативно, так же, как единичный круг
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
s
{\displaystyle s}
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
s
)
,
y
(
s
)
)
=
(
cos
s
,
sin
s
)
,
{\displaystyle (x(s),y(s))=(\cos s,\sin s),}
L
{\displaystyle {\mathcal {L}}}
s
{\displaystyle s}
(
1
,
0
)
{\displaystyle (1,0)}
[ 31 ]
(
x
(
s
)
,
y
(
s
)
)
=
(
cl
s
1
+
sl
2
s
,
sl
s
cl
s
1
+
sl
2
s
)
=
(
cl
~
s
,
sl
~
s
)
.
{\displaystyle (x(s),y(s))=\left({\frac {\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}},{\frac {\operatorname {sl} s\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}}\right)=\left({\tilde {\operatorname {cl} }}\,s,{\tilde {\operatorname {sl} }}\,s\right).}
Обозначения
cl
~
,
sl
~
{\displaystyle {\tilde {\operatorname {cl} }},\,{\tilde {\operatorname {sl} }}}
Интеграл лемнискаты и функции лемнискаты удовлетворяют тождеству дублирования аргументов, открытому Фаньяно в 1718 году: [ 32 ]
∫
0
z
d
t
1
−
t
4
=
2
∫
0
u
d
t
1
−
t
4
,
if
z
=
2
u
1
−
u
4
1
+
u
4
and
0
≤
u
≤
2
−
1
.
{\displaystyle \int _{0}^{z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=2\int _{0}^{u}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}},\quad {\text{if }}z={\frac {2u{\sqrt {1-u^{4}}}}{1+u^{4}}}{\text{ and }}0\leq u\leq {\sqrt {{\sqrt {2}}-1}}.}
Лемниската разделена на 15 секций одинаковой длины дуги (красные кривые). Поскольку простые делители 15 (3 и 5) являются простыми числами Ферма, этот многоугольник (черный) можно построить с помощью линейки и циркуля. Позднее математики обобщили этот результат. Аналогично строящимся многоугольникам в круге, лемнискату можно разделить на n линейку и циркуль тогда и только тогда, когда n
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k целое число , а каждое p i число Ферма . [ 33 ] Нильсом Абелем в 1827–1828 годах, а часть «только если» была доказана Майклом Розеном в 1981 году. [ 34 ] n
φ
(
n
)
{\displaystyle \varphi (n)}
φ
{\displaystyle \varphi }
полная функция Эйлера ). лемниската Не предполагается, что уже нарисована; теорема относится только к построению точек деления.
Позволять
r
j
=
sl
2
j
ϖ
n
{\displaystyle r_{j}=\operatorname {sl} {\dfrac {2j\varpi }{n}}}
n
L
{\displaystyle {\mathcal {L}}}
(
r
j
1
2
(
1
+
r
j
2
)
,
(
−
1
)
⌊
4
j
/
n
⌋
1
2
r
j
2
(
1
−
r
j
2
)
)
,
j
∈
{
1
,
2
,
…
,
n
}
{\displaystyle \left(r_{j}{\sqrt {{\tfrac {1}{2}}{\bigl (}1+r_{j}^{2}{\bigr )}}},\ (-1)^{\left\lfloor 4j/n\right\rfloor }{\sqrt {{\tfrac {1}{2}}r_{j}^{2}{\bigl (}1-r_{j}^{2}{\bigr )}}}\right),\quad j\in \{1,2,\ldots ,n\}}
где
⌊
⋅
⌋
{\displaystyle \lfloor \cdot \rfloor }
функция пола . приведены Ниже некоторые конкретные значения
sl
2
ϖ
n
{\displaystyle \operatorname {sl} {\dfrac {2\varpi }{n}}}
Лемнискатный синус связывает длину дуги с координатой x в прямоугольной эластике. Обратный лемнискатный синус также описывает длину дуги s координаты x эластики . [ 35 ] координату y
y
=
∫
x
1
t
2
d
t
1
−
t
4
,
s
=
arcsl
x
=
∫
0
x
d
t
1
−
t
4
{\displaystyle y=\int _{x}^{1}{\frac {t^{2}\mathop {\mathrm {d} t} }{\sqrt {1-t^{4}}}},\quad s=\operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}}
Прямоугольная эластика решает задачу, поставленную Якобом Бернулли в 1691 году для описания формы идеализированного гибкого стержня, закрепленного в вертикальном положении на нижнем конце и притягиваемого вниз под действием веса с дальнего конца до тех пор, пока он не согнется горизонтально. Предложенное Бернулли решение положило начало теории пучка Эйлера-Бернулли , получившей дальнейшее развитие Эйлера в 18 веке.
Лемнискатные эллиптические функции и эллипс Позволять
C
{\displaystyle C}
x
2
+
2
y
2
=
1
{\displaystyle x^{2}+2y^{2}=1}
D
{\displaystyle D}
C
{\displaystyle C}
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
r
{\displaystyle r}
A
{\displaystyle A}
C
{\displaystyle C}
φ
{\displaystyle \varphi }
B
A
C
{\displaystyle BAC}
B
=
(
1
,
0
)
{\displaystyle B=(1,0)}
B
D
{\displaystyle BD}
u
{\displaystyle u}
u
=
∫
0
φ
r
(
θ
)
d
θ
=
∫
0
φ
d
θ
1
+
sin
2
θ
.
{\displaystyle u=\int _{0}^{\varphi }r(\theta )\,\mathrm {d} \theta =\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1+\sin ^{2}\theta }}}.}
Если
E
{\displaystyle E}
D
{\displaystyle D}
F
{\displaystyle F}
C
{\displaystyle C}
cl
u
=
A
F
¯
,
sl
u
=
D
E
¯
,
{\displaystyle \operatorname {cl} u={\overline {AF}},\quad \operatorname {sl} u={\overline {DE}},}
cl
~
u
=
A
F
¯
A
C
¯
,
sl
~
u
=
A
F
¯
F
C
¯
.
{\displaystyle {\tilde {\operatorname {cl} }}\,u={\overline {AF}}{\overline {AC}},\quad {\tilde {\operatorname {sl} }}\,u={\overline {AF}}{\overline {FC}}.}
в степенной ряд равно Разложение лемнискатного синуса в начале координат [ 36 ]
sl
z
=
∑
n
=
0
∞
a
n
z
n
=
z
−
12
z
5
5
!
+
3024
z
9
9
!
−
4390848
z
13
13
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }a_{n}z^{n}=z-12{\frac {z^{5}}{5!}}+3024{\frac {z^{9}}{9!}}-4390848{\frac {z^{13}}{13!}}+\cdots ,\quad |z|<{\tfrac {\varpi }{\sqrt {2}}}}
где коэффициенты
a
n
{\displaystyle a_{n}}
n
≢
1
(
mod
4
)
⟹
a
n
=
0
,
{\displaystyle n\not \equiv 1{\pmod {4}}\implies a_{n}=0,}
a
1
=
1
,
∀
n
∈
N
0
:
a
n
+
2
=
−
2
(
n
+
1
)
(
n
+
2
)
∑
i
+
j
+
k
=
n
a
i
a
j
a
k
{\displaystyle a_{1}=1,\,\forall n\in \mathbb {N} _{0}:\,a_{n+2}=-{\frac {2}{(n+1)(n+2)}}\sum _{i+j+k=n}a_{i}a_{j}a_{k}}
где
i
+
j
+
k
=
n
{\displaystyle i+j+k=n}
композиции обозначает все
n
{\displaystyle n}
a
13
{\displaystyle a_{13}}
13
−
2
=
11
{\displaystyle 13-2=11}
11
=
9
+
1
+
1
=
1
+
9
+
1
=
1
+
1
+
9
{\displaystyle 11=9+1+1=1+9+1=1+1+9}
11
=
5
+
5
+
1
=
5
+
1
+
5
=
1
+
5
+
5
{\displaystyle 11=5+5+1=5+1+5=1+5+5}
a
13
=
−
2
12
⋅
13
(
a
9
a
1
a
1
+
a
1
a
9
a
1
+
a
1
a
1
a
9
+
a
5
a
5
a
1
+
a
5
a
1
a
5
+
a
1
a
5
a
5
)
=
−
11
15600
.
{\displaystyle a_{13}=-{\tfrac {2}{12\cdot 13}}(a_{9}a_{1}a_{1}+a_{1}a_{9}a_{1}+a_{1}a_{1}a_{9}+a_{5}a_{5}a_{1}+a_{5}a_{1}a_{5}+a_{1}a_{5}a_{5})=-{\tfrac {11}{15600}}.}
Разложение можно эквивалентно записать как [ 37 ]
sl
z
=
∑
n
=
0
∞
p
2
n
z
4
n
+
1
(
4
n
+
1
)
!
,
|
z
|
<
ϖ
2
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }p_{2n}{\frac {z^{4n+1}}{(4n+1)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}}
где
p
n
+
2
=
−
12
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
p
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
p
k
p
j
−
k
,
p
0
=
1
,
p
1
=
0.
{\displaystyle p_{n+2}=-12\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}p_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}p_{k}p_{j-k},\quad p_{0}=1,\,p_{1}=0.}
Разложение в степенной ряд
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
sl
~
z
=
∑
n
=
0
∞
α
n
z
n
=
z
−
9
z
3
3
!
+
153
z
5
5
!
−
4977
z
7
7
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\sum _{n=0}^{\infty }\alpha _{n}z^{n}=z-9{\frac {z^{3}}{3!}}+153{\frac {z^{5}}{5!}}-4977{\frac {z^{7}}{7!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}}}
где
α
n
=
0
{\displaystyle \alpha _{n}=0}
n
{\displaystyle n}
[ 38 ]
α
n
=
2
π
ϖ
(
−
1
)
(
n
−
1
)
/
2
n
!
∑
k
=
1
∞
(
2
k
π
/
ϖ
)
n
+
1
cosh
k
π
,
|
α
n
|
∼
2
n
+
5
/
2
n
+
1
ϖ
n
+
2
{\displaystyle \alpha _{n}={\sqrt {2}}{\frac {\pi }{\varpi }}{\frac {(-1)^{(n-1)/2}}{n!}}\sum _{k=1}^{\infty }{\frac {(2k\pi /\varpi )^{n+1}}{\cosh k\pi }},\quad \left|\alpha _{n}\right|\sim 2^{n+5/2}{\frac {n+1}{\varpi ^{n+2}}}}
если
n
{\displaystyle n}
Разложение можно эквивалентно записать как [ 39 ]
sl
~
z
=
∑
n
=
0
∞
(
−
1
)
n
2
n
+
1
(
∑
l
=
0
n
2
l
(
2
n
+
2
2
l
+
1
)
s
l
t
n
−
l
)
z
2
n
+
1
(
2
n
+
1
)
!
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2^{n+1}}}\left(\sum _{l=0}^{n}2^{l}{\binom {2n+2}{2l+1}}s_{l}t_{n-l}\right){\frac {z^{2n+1}}{(2n+1)!}},\quad \left|z\right|<{\frac {\varpi }{2}}}
где
s
n
+
2
=
3
s
n
+
1
+
24
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
s
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
s
k
s
j
−
k
,
s
0
=
1
,
s
1
=
3
,
{\displaystyle s_{n+2}=3s_{n+1}+24\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}s_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}s_{k}s_{j-k},\quad s_{0}=1,\,s_{1}=3,}
t
n
+
2
=
3
t
n
+
1
+
3
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
t
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
t
k
t
j
−
k
,
t
0
=
1
,
t
1
=
3.
{\displaystyle t_{n+2}=3t_{n+1}+3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}t_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}t_{k}t_{j-k},\quad t_{0}=1,\,t_{1}=3.}
Для лемнискатного косинуса [ 40 ]
cl
z
=
1
−
∑
n
=
0
∞
(
−
1
)
n
(
∑
l
=
0
n
2
l
(
2
n
+
2
2
l
+
1
)
q
l
r
n
−
l
)
z
2
n
+
2
(
2
n
+
2
)
!
=
1
−
2
z
2
2
!
+
12
z
4
4
!
−
216
z
6
6
!
+
⋯
,
|
z
|
<
ϖ
2
,
{\displaystyle \operatorname {cl} {z}=1-\sum _{n=0}^{\infty }(-1)^{n}\left(\sum _{l=0}^{n}2^{l}{\binom {2n+2}{2l+1}}q_{l}r_{n-l}\right){\frac {z^{2n+2}}{(2n+2)!}}=1-2{\frac {z^{2}}{2!}}+12{\frac {z^{4}}{4!}}-216{\frac {z^{6}}{6!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}},}
cl
~
z
=
∑
n
=
0
∞
(
−
1
)
n
2
n
q
n
z
2
n
(
2
n
)
!
=
1
−
3
z
2
2
!
+
33
z
4
4
!
−
819
z
6
6
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,z=\sum _{n=0}^{\infty }(-1)^{n}2^{n}q_{n}{\frac {z^{2n}}{(2n)!}}=1-3{\frac {z^{2}}{2!}}+33{\frac {z^{4}}{4!}}-819{\frac {z^{6}}{6!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}}}
где
r
n
+
2
=
3
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
r
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
r
k
r
j
−
k
,
r
0
=
1
,
r
1
=
0
,
{\displaystyle r_{n+2}=3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}r_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}r_{k}r_{j-k},\quad r_{0}=1,\,r_{1}=0,}
q
n
+
2
=
3
2
q
n
+
1
+
6
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
q
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
q
k
q
j
−
k
,
q
0
=
1
,
q
1
=
3
2
.
{\displaystyle q_{n+2}={\tfrac {3}{2}}q_{n+1}+6\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}q_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}q_{k}q_{j-k},\quad q_{0}=1,\,q_{1}={\tfrac {3}{2}}.}
Знаменитая идентичность cos/cosh Рамануджана гласит, что если
R
(
s
)
=
π
ϖ
2
∑
n
∈
Z
cos
(
2
n
π
s
/
ϖ
)
cosh
n
π
,
{\displaystyle R(s)={\frac {\pi }{\varpi {\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {\cos(2n\pi s/\varpi )}{\cosh n\pi }},}
затем [ 38 ]
R
(
s
)
−
2
+
R
(
i
s
)
−
2
=
2
,
|
Re
s
|
<
ϖ
2
,
|
Im
s
|
<
ϖ
2
.
{\displaystyle R(s)^{-2}+R(is)^{-2}=2,\quad \left|\operatorname {Re} s\right|<{\frac {\varpi }{2}},\left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}.}
Существует тесная связь между лемнискатными функциями и
R
(
s
)
{\displaystyle R(s)}
[ 38 ] [ 41 ]
sl
~
s
=
−
d
d
s
R
(
s
)
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,s=-{\frac {\mathrm {d} }{\mathrm {d} s}}R(s)\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
cl
~
s
=
d
d
s
1
−
R
(
s
)
2
,
|
Re
s
−
ϖ
2
|
<
ϖ
2
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\frac {\mathrm {d} }{\mathrm {d} s}}{\sqrt {1-R(s)^{2}}},\quad \left|\operatorname {Re} s-{\frac {\varpi }{2}}\right|<{\frac {\varpi }{2}},\,\left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
и
R
(
s
)
=
1
1
+
sl
2
s
,
|
Im
s
|
<
ϖ
2
.
{\displaystyle R(s)={\frac {1}{\sqrt {1+\operatorname {sl} ^{2}s}}},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}.}
Для
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
[ 42 ]
∫
0
∞
e
−
t
z
2
cl
t
d
t
=
1
/
2
z
+
a
1
z
+
a
2
z
+
a
3
z
+
⋱
,
a
n
=
n
2
4
(
(
−
1
)
n
+
1
+
3
)
{\displaystyle \int _{0}^{\infty }e^{-tz{\sqrt {2}}}\operatorname {cl} t\,\mathrm {d} t={\cfrac {1/{\sqrt {2}}}{z+{\cfrac {a_{1}}{z+{\cfrac {a_{2}}{z+{\cfrac {a_{3}}{z+\ddots }}}}}}}},\quad a_{n}={\frac {n^{2}}{4}}((-1)^{n+1}+3)}
∫
0
∞
e
−
t
z
2
sl
t
cl
t
d
t
=
1
/
2
z
2
+
b
1
−
a
1
z
2
+
b
2
−
a
2
z
2
+
b
3
−
⋱
,
a
n
=
n
2
(
4
n
2
−
1
)
,
b
n
=
3
(
2
n
−
1
)
2
{\displaystyle \int _{0}^{\infty }e^{-tz{\sqrt {2}}}\operatorname {sl} t\operatorname {cl} t\,\mathrm {d} t={\cfrac {1/2}{z^{2}+b_{1}-{\cfrac {a_{1}}{z^{2}+b_{2}-{\cfrac {a_{2}}{z^{2}+b_{3}-\ddots }}}}}},\quad a_{n}=n^{2}(4n^{2}-1),\,b_{n}=3(2n-1)^{2}}
Несколько методов расчета
sl
x
{\displaystyle \operatorname {sl} x}
π
x
=
ϖ
x
~
{\displaystyle \pi x=\varpi {\tilde {x}}}
sl
(
ϖ
x
~
/
π
)
.
{\displaystyle \operatorname {sl} (\varpi {\tilde {x}}/\pi ).}
рядов Метод гиперболических : [ 45 ] [ 46 ] [ 47 ]
sl
(
ϖ
π
x
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
cosh
(
x
−
(
n
+
1
/
2
)
π
)
,
x
∈
C
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\cosh(x-(n+1/2)\pi )}},\quad x\in \mathbb {C} }
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sinh
(
x
−
n
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sin
(
x
−
n
π
i
)
,
x
∈
C
{\displaystyle {\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{{\sinh }{\left(x-n\pi \right)}}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\sin(x-n\pi i)}},\quad x\in \mathbb {C} }
Метод рядов Фурье : [ 48 ]
sl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
(
−
1
)
n
sin
(
(
2
n
+
1
)
x
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {(-1)^{n}\sin((2n+1)x)}{\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
cl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
cos
(
(
2
n
+
1
)
x
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {\cos((2n+1)x)}{\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
(
1
sin
x
−
4
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
e
(
2
n
+
1
)
π
+
1
)
,
|
Im
x
|
<
π
{\displaystyle {\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\left({\frac {1}{\sin x}}-4\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{e^{(2n+1)\pi }+1}}\right),\quad \left|\operatorname {Im} x\right|<\pi }
Лемнискатные функции можно вычислить быстрее, если
sl
(
ϖ
π
x
)
=
θ
1
(
x
,
e
−
π
)
θ
3
(
x
,
e
−
π
)
,
x
∈
C
cl
(
ϖ
π
x
)
=
θ
2
(
x
,
e
−
π
)
θ
4
(
x
,
e
−
π
)
,
x
∈
C
{\displaystyle {\begin{aligned}\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}&={\frac {{\theta _{1}}{\left(x,e^{-\pi }\right)}}{{\theta _{3}}{\left(x,e^{-\pi }\right)}}},\quad x\in \mathbb {C} \\\operatorname {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}&={\frac {{\theta _{2}}{\left(x,e^{-\pi }\right)}}{{\theta _{4}}{\left(x,e^{-\pi }\right)}}},\quad x\in \mathbb {C} \end{aligned}}}
где
θ
1
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
+
1
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
1
/
2
)
2
sin
(
(
2
n
+
1
)
x
)
,
θ
2
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
)
2
cos
(
(
2
n
+
1
)
x
)
,
θ
3
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
n
2
cos
2
n
x
,
θ
4
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
n
2
cos
2
n
x
{\displaystyle {\begin{aligned}\theta _{1}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }(-1)^{n+1}e^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi (n+1/2)^{2}}\sin((2n+1)x),\\\theta _{2}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }e^{-\pi (n+1/2)^{2}}\cos((2n+1)x),\\\theta _{3}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}\cos 2nx,\\\theta _{4}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }e^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi n^{2}}\cos 2nx\end{aligned}}}
— тэта-функции Якоби . [ 49 ]
Ряд Фурье для логарифма лемнискатного синуса:
ln
sl
(
ϖ
π
x
)
=
ln
2
−
π
4
+
ln
sin
x
+
2
∑
n
=
1
∞
(
−
1
)
n
cos
2
n
x
n
(
e
n
π
+
(
−
1
)
n
)
,
|
Im
x
|
<
π
2
{\displaystyle \ln \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=\ln 2-{\frac {\pi }{4}}+\ln \sin x+2\sum _{n=1}^{\infty }{\frac {(-1)^{n}\cos 2nx}{n(e^{n\pi }+(-1)^{n})}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
Следующие серии личностей были обнаружены Рамануджаном : [ 50 ]
ϖ
2
π
2
sl
2
(
ϖ
x
/
π
)
=
1
sin
2
x
−
1
π
−
8
∑
n
=
1
∞
n
cos
2
n
x
e
2
n
π
−
1
,
|
Im
x
|
<
π
{\displaystyle {\frac {\varpi ^{2}}{\pi ^{2}\operatorname {sl} ^{2}(\varpi x/\pi )}}={\frac {1}{\sin ^{2}x}}-{\frac {1}{\pi }}-8\sum _{n=1}^{\infty }{\frac {n\cos 2nx}{e^{2n\pi }-1}},\quad \left|\operatorname {Im} x\right|<\pi }
arctan
sl
(
ϖ
π
x
)
=
2
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
(
2
n
+
1
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \arctan \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{(2n+1)\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
Функции
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
[ 38 ] [ 41 ] [ 51 ]
sl
~
s
=
2
2
π
2
ϖ
2
∑
n
=
1
∞
n
sin
(
2
n
π
s
/
ϖ
)
cosh
n
π
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,s=2{\sqrt {2}}{\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n=1}^{\infty }{\frac {n\sin(2n\pi s/\varpi )}{\cosh n\pi }},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
cl
~
s
=
2
π
2
ϖ
2
∑
n
=
0
∞
(
2
n
+
1
)
cos
(
(
2
n
+
1
)
π
s
/
ϖ
)
sinh
(
(
n
+
1
/
2
)
π
)
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\sqrt {2}}{\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n=0}^{\infty }{\frac {(2n+1)\cos((2n+1)\pi s/\varpi )}{\sinh((n+1/2)\pi )}},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
sl
~
s
=
π
2
ϖ
2
2
∑
n
∈
Z
sinh
(
π
(
n
+
s
/
ϖ
)
)
cosh
2
(
π
(
n
+
s
/
ϖ
)
)
,
s
∈
C
{\displaystyle {\tilde {\operatorname {sl} }}\,s={\frac {\pi ^{2}}{\varpi ^{2}{\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {\sinh(\pi (n+s/\varpi ))}{\cosh ^{2}(\pi (n+s/\varpi ))}},\quad s\in \mathbb {C} }
cl
~
s
=
π
2
ϖ
2
2
∑
n
∈
Z
(
−
1
)
n
cosh
2
(
π
(
n
+
s
/
ϖ
)
)
,
s
∈
C
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\frac {\pi ^{2}}{\varpi ^{2}{\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\cosh ^{2}(\pi (n+s/\varpi ))}},\quad s\in \mathbb {C} }
Два других метода быстрых вычислений используют следующую сумму и ряд произведений:
Следующие тождества происходят из представлений произведений тэта-функций: [ 52 ]
s
l
(
ϖ
π
x
)
=
2
e
−
π
/
4
sin
x
∏
n
=
1
∞
1
−
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
+
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
x
∈
C
{\displaystyle \mathrm {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2e^{-\pi /4}\sin x\prod _{n=1}^{\infty }{\frac {1-2e^{-2n\pi }\cos 2x+e^{-4n\pi }}{1+2e^{-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi }}},\quad x\in \mathbb {C} }
c
l
(
ϖ
π
x
)
=
2
e
−
π
/
4
cos
x
∏
n
=
1
∞
1
+
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
−
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
x
∈
C
{\displaystyle \mathrm {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2e^{-\pi /4}\cos x\prod _{n=1}^{\infty }{\frac {1+2e^{-2n\pi }\cos 2x+e^{-4n\pi }}{1-2e^{-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi }}},\quad x\in \mathbb {C} }
Аналогичная формула, включающая
sn
{\displaystyle \operatorname {sn} }
[ 53 ]
По той же схеме с помощью теоремы касательного удвоения можно составить следующие формулы сумм:
sl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
sin
x
∑
n
=
1
∞
cosh
[
(
2
n
−
1
)
π
]
cosh
2
[
(
2
n
−
1
)
π
]
−
cos
2
x
)
{\displaystyle {\text{sl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\cos ^{2}x}}{\biggr )}}
cl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
cos
x
∑
n
=
1
∞
cosh
[
(
2
n
−
1
)
π
]
cosh
2
[
(
2
n
−
1
)
π
]
−
sin
2
x
)
{\displaystyle {\text{cl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\cos x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\sin ^{2}x}}{\biggr )}}
где
f
(
x
)
=
tan
(
2
arctan
x
)
=
2
x
/
(
1
−
x
2
)
.
{\displaystyle f(x)=\tan(2\arctan x)=2x/(1-x^{2}).}
Лемниската функционирует как отношение целых функций. [ редактировать ] Поскольку лемнискатный синус является мероморфной функцией во всей комплексной плоскости, его можно записать как отношение целых функций . Гаусс показал, что sl имеет следующее разложение произведения, отражающее распределение его нулей и полюсов: [ 54 ]
sl
z
=
M
(
z
)
N
(
z
)
{\displaystyle \operatorname {sl} z={\frac {M(z)}{N(z)}}}
где
M
(
z
)
=
z
∏
α
(
1
−
z
4
α
4
)
,
N
(
z
)
=
∏
β
(
1
−
z
4
β
4
)
.
{\displaystyle M(z)=z\prod _{\alpha }\left(1-{\frac {z^{4}}{\alpha ^{4}}}\right),\quad N(z)=\prod _{\beta }\left(1-{\frac {z^{4}}{\beta ^{4}}}\right).}
Здесь,
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
sl , находящиеся в квадранте
Re
z
>
0
,
Im
z
≥
0
{\displaystyle \operatorname {Re} z>0,\operatorname {Im} z\geq 0}
[ 54 ] [ 55 ] равномерной сходимости . [ 56 ]
показывать Доказательство бесконечного произведения лемнискатного синуса.
It can be easily seen (using uniform and absolute convergence arguments to justify interchanging of limiting operations ) that
M
′
(
z
)
M
(
z
)
=
−
∑
n
=
0
∞
2
4
n
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
{\displaystyle {\frac {M'(z)}{M(z)}}=-\sum _{n=0}^{\infty }2^{4n}\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<\varpi }
(where
H
n
{\displaystyle \mathrm {H} _{n}}
Lemniscate elliptic functions § Hurwitz numbers ) and
N
′
(
z
)
N
(
z
)
=
(
1
+
i
)
M
′
(
(
1
+
i
)
z
)
M
(
(
1
+
i
)
z
)
−
M
′
(
z
)
M
(
z
)
.
{\displaystyle {\frac {N'(z)}{N(z)}}=(1+i){\frac {M'((1+i)z)}{M((1+i)z)}}-{\frac {M'(z)}{M(z)}}.}
Therefore
N
′
(
z
)
N
(
z
)
=
∑
n
=
0
∞
2
4
n
(
1
−
(
−
1
)
n
2
2
n
)
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {N'(z)}{N(z)}}=\sum _{n=0}^{\infty }2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
It is known that
1
sl
2
z
=
∑
n
=
0
∞
2
4
n
(
4
n
−
1
)
H
4
n
z
4
n
−
2
(
4
n
)
!
,
|
z
|
<
ϖ
.
{\displaystyle {\frac {1}{\operatorname {sl} ^{2}z}}=\sum _{n=0}^{\infty }2^{4n}(4n-1)\mathrm {H} _{4n}{\frac {z^{4n-2}}{(4n)!}},\quad \left|z\right|<\varpi .}
Then from
d
d
z
sl
′
z
sl
z
=
−
1
sl
2
z
−
sl
2
z
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}{\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}=-{\frac {1}{\operatorname {sl} ^{2}z}}-\operatorname {sl} ^{2}z}
and
sl
2
z
=
1
sl
2
z
−
(
1
+
i
)
2
sl
2
(
(
1
+
i
)
z
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\operatorname {sl} ^{2}z}}-{\frac {(1+i)^{2}}{\operatorname {sl} ^{2}((1+i)z)}}}
we get
sl
′
z
sl
z
=
−
∑
n
=
0
∞
2
4
n
(
2
−
(
−
1
)
n
2
2
n
)
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}=-\sum _{n=0}^{\infty }2^{4n}(2-(-1)^{n}2^{2n})\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
Hence
sl
′
z
sl
z
=
M
′
(
z
)
M
(
z
)
−
N
′
(
z
)
N
(
z
)
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}={\frac {M'(z)}{M(z)}}-{\frac {N'(z)}{N(z)}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
Therefore
sl
z
=
C
M
(
z
)
N
(
z
)
{\displaystyle \operatorname {sl} z=C{\frac {M(z)}{N(z)}}}
for some constant
C
{\displaystyle C}
|
z
|
<
ϖ
/
2
{\displaystyle \left|z\right|<\varpi /{\sqrt {2}}}
z
∈
C
{\displaystyle z\in \mathbb {C} }
lim
z
→
0
sl
z
z
=
1
{\displaystyle \lim _{z\to 0}{\frac {\operatorname {sl} z}{z}}=1}
gives
C
=
1
{\displaystyle C=1}
◼
{\displaystyle \blacksquare }
Гаусс предположил, что
ln
N
(
ϖ
)
=
π
/
2
{\displaystyle \ln N(\varpi )=\pi /2}
[ 57 ]
M
{\displaystyle M}
N
{\displaystyle N}
M
{\displaystyle M}
N
{\displaystyle N}
The
M
{\displaystyle M}
The
N
{\displaystyle N}
N
(
z
)
=
M
(
(
1
+
i
)
z
)
(
1
+
i
)
M
(
z
)
,
z
∉
ϖ
Z
[
i
]
{\displaystyle N(z)={\frac {M((1+i)z)}{(1+i)M(z)}},\quad z\notin \varpi \mathbb {Z} [i]}
и
N
(
2
z
)
=
M
(
z
)
4
+
N
(
z
)
4
.
{\displaystyle N(2z)=M(z)^{4}+N(z)^{4}.}
Благодаря некоторой теореме [ 58 ]
z
{\displaystyle z}
[ 59 ] [ 60 ] [ 61 ] [ 62 ]
M
(
z
)
=
z
−
2
z
5
5
!
−
36
z
9
9
!
+
552
z
13
13
!
+
⋯
,
z
∈
C
{\displaystyle M(z)=z-2{\frac {z^{5}}{5!}}-36{\frac {z^{9}}{9!}}+552{\frac {z^{13}}{13!}}+\cdots ,\quad z\in \mathbb {C} }
N
(
z
)
=
1
+
2
z
4
4
!
−
4
z
8
8
!
+
408
z
12
12
!
+
⋯
,
z
∈
C
.
{\displaystyle N(z)=1+2{\frac {z^{4}}{4!}}-4{\frac {z^{8}}{8!}}+408{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} .}
Это можно сравнить со степенным рядом
sl
{\displaystyle \operatorname {sl} }
Мы определяем
S
{\displaystyle S}
T
{\displaystyle T}
S
(
z
)
=
N
(
z
1
+
i
)
2
−
i
M
(
z
1
+
i
)
2
,
T
(
z
)
=
S
(
i
z
)
.
{\displaystyle S(z)=N\left({\frac {z}{1+i}}\right)^{2}-iM\left({\frac {z}{1+i}}\right)^{2},\quad T(z)=S(iz).}
Тогда лемнискатный косинус можно записать как
cl
z
=
S
(
z
)
T
(
z
)
{\displaystyle \operatorname {cl} z={\frac {S(z)}{T(z)}}}
где [ 63 ]
S
(
z
)
=
1
−
z
2
2
!
−
z
4
4
!
−
3
z
6
6
!
+
17
z
8
8
!
−
9
z
10
10
!
+
111
z
12
12
!
+
⋯
,
z
∈
C
{\displaystyle S(z)=1-{\frac {z^{2}}{2!}}-{\frac {z^{4}}{4!}}-3{\frac {z^{6}}{6!}}+17{\frac {z^{8}}{8!}}-9{\frac {z^{10}}{10!}}+111{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} }
T
(
z
)
=
1
+
z
2
2
!
−
z
4
4
!
+
3
z
6
6
!
+
17
z
8
8
!
+
9
z
10
10
!
+
111
z
12
12
!
+
⋯
,
z
∈
C
.
{\displaystyle T(z)=1+{\frac {z^{2}}{2!}}-{\frac {z^{4}}{4!}}+3{\frac {z^{6}}{6!}}+17{\frac {z^{8}}{8!}}+9{\frac {z^{10}}{10!}}+111{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} .}
Кроме того, тождества
M
(
2
z
)
=
2
M
(
z
)
N
(
z
)
S
(
z
)
T
(
z
)
,
{\displaystyle M(2z)=2M(z)N(z)S(z)T(z),}
S
(
2
z
)
=
S
(
z
)
4
−
2
M
(
z
)
4
,
{\displaystyle S(2z)=S(z)^{4}-2M(z)^{4},}
T
(
2
z
)
=
T
(
z
)
4
−
2
M
(
z
)
4
{\displaystyle T(2z)=T(z)^{4}-2M(z)^{4}}
и пифагорейские идентичности
M
(
z
)
2
+
S
(
z
)
2
=
N
(
z
)
2
,
{\displaystyle M(z)^{2}+S(z)^{2}=N(z)^{2},}
M
(
z
)
2
+
N
(
z
)
2
=
T
(
z
)
2
{\displaystyle M(z)^{2}+N(z)^{2}=T(z)^{2}}
держись за всех
z
∈
C
{\displaystyle z\in \mathbb {C} }
Альтернативный способ выражения лемнискатных функций как отношения целых функций включает в себя тета-функции (см. Лемнискатные эллиптические функции § Методы вычислений ; тета-функции и вышеуказанные функции не эквивалентны).
Связь с эллиптическими функциями Вейерштрасса и Якоби. [ редактировать ] Функции лемнискат тесно связаны с эллиптической функцией Вейерштрасса.
℘
(
z
;
1
,
0
)
{\displaystyle \wp (z;1,0)}
g 2 = 1 g 3 = 0
ω
1
=
2
ϖ
,
{\displaystyle \omega _{1}={\sqrt {2}}\varpi ,}
ω
2
=
i
ω
1
{\displaystyle \omega _{2}=i\omega _{1}}
e
1
=
1
2
,
e
2
=
0
,
e
3
=
−
1
2
.
{\displaystyle e_{1}={\tfrac {1}{2}},\ e_{2}=0,\ e_{3}=-{\tfrac {1}{2}}.}
Связанный случай эллиптической функции Вейерштрасса с g 2 = a g 3 = 0 a > 0 a < 0 Параллелограмм представляет собой либо квадрат , либо ромб . Эллиптическая функция Вейерштрасса
℘
(
z
;
−
1
,
0
)
{\displaystyle \wp (z;-1,0)}
[ 64 ]
Квадрат лемнискатного синуса можно представить как
sl
2
z
=
1
℘
(
z
;
4
,
0
)
=
i
2
℘
(
(
1
−
i
)
z
;
−
1
,
0
)
=
−
2
℘
(
2
z
+
(
i
−
1
)
ϖ
2
;
1
,
0
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {i}{2\wp ((1-i)z;-1,0)}}={-2\wp }{\left({\sqrt {2}}z+(i-1){\frac {\varpi }{\sqrt {2}}};1,0\right)}}
где второй и третий аргумент
℘
{\displaystyle \wp }
g 2 g 3 рациональная функция в эллиптической функции Вейерштрасса и ее производной: [ 65 ]
sl
z
=
−
2
℘
(
z
;
−
1
,
0
)
℘
′
(
z
;
−
1
,
0
)
.
{\displaystyle \operatorname {sl} z=-2{\frac {\wp (z;-1,0)}{\wp '(z;-1,0)}}.}
Лемнискатные функции также можно записать через эллиптические функции Якоби . Эллиптические функции Якоби
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
i
sd
{\displaystyle \operatorname {sd} }
cn
{\displaystyle \operatorname {cn} }
1
/
2
{\displaystyle 1/{\sqrt {2}}}
[ 66 ] [ 67 ]
sl
z
=
sn
(
z
;
i
)
=
sc
(
z
;
2
)
=
1
2
sd
(
2
z
;
1
2
)
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;i)=\operatorname {sc} (z;{\sqrt {2}})={{\tfrac {1}{\sqrt {2}}}\operatorname {sd} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
cl
z
=
cd
(
z
;
i
)
=
dn
(
z
;
2
)
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
где вторые аргументы обозначают эллиптический модуль
k
{\displaystyle k}
Функции
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sl
~
z
=
cd
(
z
;
i
)
sd
(
z
;
i
)
=
dn
(
z
;
2
)
sn
(
z
;
2
)
=
1
2
cn
(
2
z
;
1
2
)
sn
(
2
z
;
1
2
)
,
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\operatorname {cd} (z;i)\operatorname {sd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})\operatorname {sn} (z;{\sqrt {2}})={\tfrac {1}{\sqrt {2}}}\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)\operatorname {sn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}
cl
~
z
=
cd
(
z
;
i
)
nd
(
z
;
i
)
=
dn
(
z
;
2
)
cn
(
z
;
2
)
=
cn
(
2
z
;
1
2
)
dn
(
2
z
;
1
2
)
.
{\displaystyle {\tilde {\operatorname {cl} }}\,z=\operatorname {cd} (z;i)\operatorname {nd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})\operatorname {cn} (z;{\sqrt {2}})=\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)\operatorname {dn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right).}
Лемнискатный синус можно использовать для вычисления значений модульной лямбда-функции :
∏
k
=
1
n
sl
(
2
k
−
1
2
n
+
1
ϖ
2
)
=
λ
(
(
2
n
+
1
)
i
)
1
−
λ
(
(
2
n
+
1
)
i
)
8
{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}
Например:
sl
(
1
14
ϖ
)
sl
(
3
14
ϖ
)
sl
(
5
14
ϖ
)
=
λ
(
7
i
)
1
−
λ
(
7
i
)
8
=
tan
(
1
2
arccsc
(
1
2
8
7
+
21
+
1
2
7
+
1
)
)
=
2
2
+
7
+
21
+
8
7
+
2
14
+
6
7
+
455
+
172
7
sl
(
1
18
ϖ
)
sl
(
3
18
ϖ
)
sl
(
5
18
ϖ
)
sl
(
7
18
ϖ
)
=
λ
(
9
i
)
1
−
λ
(
9
i
)
8
=
tan
(
π
4
−
arctan
(
2
2
3
−
2
3
−
2
2
−
3
3
+
3
−
1
12
4
)
)
{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1-\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )}\\[7mu]&\quad {}={\frac {2}{2+{\sqrt {7}}+{\sqrt {21+8{\sqrt {7}}}}+{\sqrt {2{14+6{\sqrt {7}}+{\sqrt {455+172{\sqrt {7}}}}}}}}}\\[18mu]&{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\[-3mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}={\tan }{\Biggl (}{\frac {\pi }{4}}-{\arctan }{\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}\end{aligned}}}
Обратная функция лемнискатного синуса - это лемнискатный арксинус, определяемый как
arcsl
x
=
∫
0
x
d
t
1
−
t
4
.
{\displaystyle \operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
Его также можно представить гипергеометрической функцией :
arcsl
x
=
x
2
F
1
(
1
2
,
1
4
;
5
4
;
x
4
)
.
{\displaystyle \operatorname {arcsl} x=x\,{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{4}};{\tfrac {5}{4}};x^{4}\right).}
Обратная функция лемнискатного косинуса — это лемнискатный арккосинус. Эта функция определяется следующим выражением:
arccl
x
=
∫
x
1
d
t
1
−
t
4
=
1
2
ϖ
−
arcsl
x
{\displaystyle \operatorname {arccl} x=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\tfrac {1}{2}}\varpi -\operatorname {arcsl} x}
Для x
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
sl
arcsl
x
=
x
{\displaystyle \operatorname {sl} \operatorname {arcsl} x=x}
cl
arccl
x
=
x
{\displaystyle \operatorname {cl} \operatorname {arccl} x=x}
Для уменьшения вдвое длины дуги лемнискаты справедливы следующие формулы:
sl
(
1
2
arcsl
x
)
=
sin
(
1
2
arcsin
x
)
sech
(
1
2
arsinh
x
)
sl
(
1
2
arcsl
x
)
2
=
tan
(
1
4
arcsin
x
2
)
{\displaystyle {\begin{aligned}{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}&={\sin }{\bigl (}{\tfrac {1}{2}}\arcsin x{\bigr )}\,{\operatorname {sech} }{\bigl (}{\tfrac {1}{2}}\operatorname {arsinh} x{\bigr )}\\{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}^{2}&={\tan }{\bigl (}{\tfrac {1}{4}}\arcsin x^{2}{\bigr )}\end{aligned}}}
Кроме того, существуют так называемые функции площади гиперболической лемнискаты:
aslh
(
x
)
=
∫
0
x
1
y
4
+
1
d
y
=
1
2
F
[
2
arctan
(
x
)
;
1
2
2
]
{\displaystyle \operatorname {aslh} (x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}
aclh
(
x
)
=
∫
x
∞
1
y
4
+
1
d
y
=
1
2
F
[
2
arccot
(
x
)
;
1
2
2
]
{\displaystyle \operatorname {aclh} (x)=\int _{x}^{\infty }{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\operatorname {arccot}(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}
aclh
(
x
)
=
ϖ
2
−
aslh
(
x
)
{\displaystyle \operatorname {aclh} (x)={\frac {\varpi }{\sqrt {2}}}-\operatorname {aslh} (x)}
aslh
(
x
)
=
2
arcsl
[
x
(
x
4
+
1
+
1
)
−
1
/
2
]
{\displaystyle \operatorname {aslh} (x)={\sqrt {2}}\operatorname {arcsl} {\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}
arcsl
(
x
)
=
2
aslh
[
x
(
1
+
1
−
x
4
)
−
1
/
2
]
{\displaystyle \operatorname {arcsl} (x)={\sqrt {2}}\operatorname {aslh} {\bigl [}x(1+{\sqrt {1-x^{4}}})^{-1/2}{\bigr ]}}
Выражение с использованием эллиптических интегралов [ редактировать ] Лежниската-арксинус и лемниската-аркосинус также могут быть выражены формой Лежандра:
Эти функции можно отобразить непосредственно, используя неполный эллиптический интеграл первого рода:
arcsl
x
=
1
2
F
(
arcsin
2
x
1
+
x
2
;
1
2
)
{\displaystyle \operatorname {arcsl} x={\frac {1}{\sqrt {2}}}F\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)}
arcsl
x
=
2
(
2
−
1
)
F
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
{\displaystyle \operatorname {arcsl} x=2({\sqrt {2}}-1)F\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)}
Длины дуг лемнискаты также можно выразить, используя только длины дуг эллипсов (вычисленные с помощью эллиптических интегралов второго рода):
arcsl
x
=
2
+
2
2
E
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
−
E
(
arcsin
2
x
1
+
x
2
;
1
2
)
+
x
1
−
x
2
2
(
1
+
x
2
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}
Лемниската арккосинус имеет следующее выражение:
arccl
x
=
1
2
F
(
arccos
x
;
1
2
)
{\displaystyle \operatorname {arccl} x={\frac {1}{\sqrt {2}}}F\left(\arccos x;{\frac {1}{\sqrt {2}}}\right)}
Лемниската-арксинус можно использовать для объединения многих функций. Вот список важных интегралов (константы интегрирования опущены):
∫
1
1
−
x
4
d
x
=
arcsl
x
{\displaystyle \int {\frac {1}{\sqrt {1-x^{4}}}}\,\mathrm {d} x=\operatorname {arcsl} x}
∫
1
(
x
2
+
1
)
(
2
x
2
+
1
)
d
x
=
arcsl
x
x
2
+
1
{\displaystyle \int {\frac {1}{\sqrt {(x^{2}+1)(2x^{2}+1)}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {x}{\sqrt {x^{2}+1}}}}
∫
1
x
4
+
6
x
2
+
1
d
x
=
arcsl
2
x
x
4
+
6
x
2
+
1
+
x
2
+
1
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}}}
∫
1
x
4
+
1
d
x
=
2
arcsl
x
x
4
+
1
+
1
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}}}
∫
1
(
1
−
x
4
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
4
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}}
∫
1
(
x
4
+
1
)
3
4
d
x
=
arcsl
x
x
4
+
1
4
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {x}{\sqrt[{4}]{x^{4}+1}}}}
∫
1
(
1
−
x
2
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
2
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{1+{\sqrt {1-x^{2}}}}}}
∫
1
(
x
2
+
1
)
3
4
d
x
=
2
arcsl
x
x
2
+
1
+
1
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{{\sqrt {x^{2}+1}}+1}}}
∫
1
(
a
x
2
+
b
x
+
c
)
3
4
d
x
=
2
2
4
a
2
c
−
a
b
2
4
arcsl
2
a
x
+
b
4
a
(
a
x
2
+
b
x
+
c
)
+
4
a
c
−
b
2
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}}
∫
sech
x
d
x
=
2
arcsl
tanh
1
2
x
{\displaystyle \int {\sqrt {\operatorname {sech} x}}\,\mathrm {d} x={2\operatorname {arcsl} }\tanh {\tfrac {1}{2}}x}
∫
sec
x
d
x
=
2
arcsl
tan
1
2
x
{\displaystyle \int {\sqrt {\sec x}}\,\mathrm {d} x={2\operatorname {arcsl} }\tan {\tfrac {1}{2}}x}
Гиперболический лемнискатный синус (красный) и гиперболический лемнискатный косинус (фиолетовый) применяются к вещественному аргументу по сравнению с тригонометрическим тангенсом (бледно-пунктирный красный). Гиперболический лемнискатный синус в комплексной плоскости. Темные области представляют собой нули, а светлые области представляют собой полюса. Сложный аргумент представлен различным оттенком. Для удобства пусть
σ
=
2
ϖ
{\displaystyle \sigma ={\sqrt {2}}\varpi }
σ
{\displaystyle \sigma }
π
{\displaystyle \pi }
σ
{\displaystyle \sigma }
3.7081
…
{\displaystyle 3.7081\ldots }
[ 68 ] [ 69 ]
Гиперболический лемнискатный синус ( slh ) и косинус ( clh ) можно определить как обратные эллиптическим интегралам следующим образом:
z
=
∗
∫
0
slh
z
d
t
1
+
t
4
=
∫
clh
z
∞
d
t
1
+
t
4
{\displaystyle z\mathrel {\overset {*}{=}} \int _{0}^{\operatorname {slh} z}{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{\operatorname {clh} z}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}}
где в
(
∗
)
{\displaystyle (*)}
z
{\displaystyle z}
{
σ
/
2
,
σ
i
/
2
,
−
σ
/
2
,
−
σ
i
/
2
}
{\displaystyle \{\sigma /2,\sigma i/2,-\sigma /2,-\sigma i/2\}}
Полный интеграл имеет значение:
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
σ
2
=
1.85407
46773
01371
…
{\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\sigma }{2}}=1.85407\;46773\;01371\ldots }
Таким образом, две определенные функции имеют следующее отношение друг к другу:
slh
z
=
clh
(
σ
2
−
z
)
{\displaystyle \operatorname {slh} z={\operatorname {clh} }{{\Bigl (}{\frac {\sigma }{2}}-z{\Bigr )}}}
Произведение гиперболического лемнискатного синуса и гиперболического лемнискатного косинуса равно единице:
slh
z
clh
z
=
1
{\displaystyle \operatorname {slh} z\,\operatorname {clh} z=1}
Функции
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
{
σ
,
σ
i
}
{\displaystyle \{\sigma ,\sigma i\}}
Гиперболические лемнискатные функции можно выразить через лемнискатный синус и лемнискатный косинус:
slh
(
2
z
)
=
(
1
+
cl
2
z
)
sl
z
2
cl
z
{\displaystyle \operatorname {slh} {\bigl (}{\sqrt {2}}z{\bigr )}={\frac {(1+\operatorname {cl} ^{2}z)\operatorname {sl} z}{{\sqrt {2}}\operatorname {cl} z}}}
clh
(
2
z
)
=
(
1
+
sl
2
z
)
cl
z
2
sl
z
{\displaystyle \operatorname {clh} {\bigl (}{\sqrt {2}}z{\bigr )}={\frac {(1+\operatorname {sl} ^{2}z)\operatorname {cl} z}{{\sqrt {2}}\operatorname {sl} z}}}
Но существует также связь с эллиптическими функциями Якоби с эллиптическим модулем, равным квадратному корню из двух:
slh
z
=
sn
(
z
;
1
/
2
)
cd
(
z
;
1
/
2
)
{\displaystyle \operatorname {slh} z={\frac {\operatorname {sn} (z;1/{\sqrt {2}})}{\operatorname {cd} (z;1/{\sqrt {2}})}}}
clh
z
=
cd
(
z
;
1
/
2
)
sn
(
z
;
1
/
2
)
{\displaystyle \operatorname {clh} z={\frac {\operatorname {cd} (z;1/{\sqrt {2}})}{\operatorname {sn} (z;1/{\sqrt {2}})}}}
Гиперболический лемнискатный синус имеет следующее мнимое отношение к лемнискатному синусу:
slh
z
=
1
−
i
2
sl
(
1
+
i
2
z
)
=
sl
(
−
1
4
z
)
−
1
4
{\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}
Это аналогично взаимосвязи между гиперболическим и тригонометрическим синусом:
sinh
z
=
−
i
sin
(
i
z
)
=
sin
(
−
1
2
z
)
−
1
2
{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}}
На этом изображении показана стандартизированная суперэллиптическая прямоугольная кривая Ферма четвертой степени:
Суперэллипс с соотношением
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
В кривой Ферма четвертой степени
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
белкой ) гиперболические лемнискатные синус и косинус аналогичны функциям тангенса и котангенса в единичном круге.
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
L L
x
=
1
{\displaystyle x=1}
[ 70 ]
π
{\displaystyle \pi }
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
σ
{\displaystyle \sigma }
M
(
1
,
1
/
2
)
=
π
σ
{\displaystyle M(1,1/{\sqrt {2}})={\frac {\pi }{\sigma }}}
где
M
{\displaystyle M}
среднее арифметико-геометрическое .
Гиперболический лемнискатный синус удовлетворяет тождеству сложения аргументов:
slh
(
a
+
b
)
=
slh
a
slh
′
b
+
slh
b
slh
′
a
1
−
slh
2
a
slh
2
b
{\displaystyle \operatorname {slh} (a+b)={\frac {\operatorname {slh} a\operatorname {slh} 'b+\operatorname {slh} b\operatorname {slh} 'a}{1-\operatorname {slh} ^{2}a\,\operatorname {slh} ^{2}b}}}
Когда
u
{\displaystyle u}
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
d
d
u
slh
(
u
)
=
1
+
slh
(
u
)
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {slh} (u)={\sqrt {1+\operatorname {slh} (u)^{4}}}}
d
d
u
clh
(
u
)
=
−
1
+
clh
(
u
)
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {clh} (u)=-{\sqrt {1+\operatorname {clh} (u)^{4}}}}
d
d
u
1
2
arsinh
[
slh
(
u
)
2
]
=
slh
(
u
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {slh} (u)^{2}{\bigr ]}=\operatorname {slh} (u)}
d
d
u
−
1
2
arsinh
[
clh
(
u
)
2
]
=
clh
(
u
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}-\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {clh} (u)^{2}{\bigr ]}=\operatorname {clh} (u)}
Существуют также гиперболический лемнискатный тангенс и гиперболический лемнискатный тангенс, а также дополнительные функции:
Функции tlh и ctlh удовлетворяют тождествам, описанным в упомянутом дифференциальном уравнении:
tlh
(
2
u
)
=
sin
4
(
2
u
)
=
sl
(
u
)
cl
2
u
+
1
sl
2
u
+
cl
2
u
{\displaystyle {\text{tlh}}({\sqrt {2}}\,u)=\sin _{4}({\sqrt {2}}\,u)=\operatorname {sl} (u){\sqrt {\frac {\operatorname {cl} ^{2}u+1}{\operatorname {sl} ^{2}u+\operatorname {cl} ^{2}u}}}}
ctlh
(
2
u
)
=
cos
4
(
2
u
)
=
cl
(
u
)
sl
2
u
+
1
sl
2
u
+
cl
2
u
{\displaystyle {\text{ctlh}}({\sqrt {2}}\,u)=\cos _{4}({\sqrt {2}}\,u)=\operatorname {cl} (u){\sqrt {\frac {\operatorname {sl} ^{2}u+1}{\operatorname {sl} ^{2}u+\operatorname {cl} ^{2}u}}}}
Функциональное обозначение sl обозначает лемнискатический синус, а обозначение cl — лемнискатический косинус.
Кроме того, эти отношения к эллиптическим функциям Якоби действительны:
tlh
(
u
)
=
sn
(
u
;
1
2
2
)
cd
(
u
;
1
2
2
)
4
+
sn
(
u
;
1
2
2
)
4
4
{\displaystyle {\text{tlh}}(u)={\frac {{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}
ctlh
(
u
)
=
cd
(
u
;
1
2
2
)
cd
(
u
;
1
2
2
)
4
+
sn
(
u
;
1
2
2
)
4
4
{\displaystyle {\text{ctlh}}(u)={\frac {{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}
Когда
u
{\displaystyle u}
tlh
{\displaystyle \operatorname {tlh} }
ctlh
{\displaystyle \operatorname {ctlh} }
d
d
u
tlh
(
u
)
=
ctlh
(
u
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {tlh} (u)=\operatorname {ctlh} (u)^{3}}
d
d
u
ctlh
(
u
)
=
−
tlh
(
u
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {ctlh} (u)=-\operatorname {tlh} (u)^{3}}
∫
0
ϖ
/
2
tlh
(
u
)
d
u
=
ϖ
2
{\displaystyle \int _{0}^{\varpi /{\sqrt {2}}}\operatorname {tlh} (u)\,\mathrm {d} u={\frac {\varpi }{2}}}
∫
0
ϖ
/
2
ctlh
(
u
)
d
u
=
ϖ
2
{\displaystyle \int _{0}^{\varpi /{\sqrt {2}}}\operatorname {ctlh} (u)\,\mathrm {d} u={\frac {\varpi }{2}}}
По отношению к кривой Ферма четвертой степени
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
sin
4
{\displaystyle \sin _{4}}
cos
4
{\displaystyle \cos _{4}}
[ 71 ] Горизонтальные и вертикальные координаты этого суперэллипса зависят от удвоенной замкнутой площади w = 2A, поэтому должны быть выполнены следующие условия:
x
(
w
)
4
+
y
(
w
)
4
=
1
{\displaystyle x(w)^{4}+y(w)^{4}=1}
d
d
w
x
(
w
)
=
−
y
(
w
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}x(w)=-y(w)^{3}}
d
d
w
y
(
w
)
=
x
(
w
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}y(w)=x(w)^{3}}
x
(
w
=
0
)
=
1
{\displaystyle x(w=0)=1}
y
(
w
=
0
)
=
0
{\displaystyle y(w=0)=0}
Решения этой системы уравнений следующие:
x
(
w
)
=
cl
(
1
2
2
w
)
[
sl
(
1
2
2
w
)
2
+
1
]
1
/
2
[
sl
(
1
2
2
w
)
2
+
cl
(
1
2
2
w
)
2
]
−
1
/
2
{\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}
y
(
w
)
=
sl
(
1
2
2
w
)
[
cl
(
1
2
2
w
)
2
+
1
]
1
/
2
[
sl
(
1
2
2
w
)
2
+
cl
(
1
2
2
w
)
2
]
−
1
/
2
{\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}
Таким образом, к фактору применимо следующее:
y
(
w
)
x
(
w
)
=
sl
(
1
2
2
w
)
[
cl
(
1
2
2
w
)
2
+
1
]
1
/
2
cl
(
1
2
2
w
)
[
sl
(
1
2
2
w
)
2
+
1
]
1
/
2
=
slh
(
w
)
{\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}}=\operatorname {slh} (w)}
Функции x(w) и y(w) называются котангенсным гиперболическим лемнискатом и гиперболическим тангенсом .
x
(
w
)
=
ctlh
(
w
)
{\displaystyle x(w)={\text{ctlh}}(w)}
y
(
w
)
=
tlh
(
w
)
{\displaystyle y(w)={\text{tlh}}(w)}
На эскизе также показано, что вывод гиперболической лемнискатной функции Areasinus равен обратной величине квадратного корня из наследника четвертой степенной функции.
Первое доказательство: сравнение с производной арктангенса [ редактировать ] На эскизе, показанном справа, есть черная диагональ. Длину отрезка, идущего перпендикулярно от пересечения этой черной диагонали с красной вертикальной осью до точки (1|0), следует назвать s. А длина участка черной диагонали от точки начала координат до точки пересечения этой диагонали с голубой изогнутой линией суперэллипса имеет следующее значение в зависимости от значения slh:
D
(
s
)
=
(
1
s
4
+
1
4
)
2
+
(
s
s
4
+
1
4
)
2
=
s
2
+
1
s
4
+
1
4
{\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}
Эта связь описывается теоремой Пифагора .
Аналогичный единичный круг дает арктангенс тригонометрического круга с описанным распределением площади.
Для этого применяется следующий вывод:
d
d
s
arctan
(
s
)
=
1
s
2
+
1
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s)={\frac {1}{s^{2}+1}}}
Чтобы определить вывод площадей sinus lemniscatus Hyperbolicus, ниже приведено сравнение бесконечно малых треугольных площадей для одной и той же диагонали в суперэллипсе и единичном круге. Потому что сумма бесконечно малых треугольных площадей описывает размеры площади. В случае суперэллипса на рисунке половина рассматриваемой области показана зеленым цветом. Из-за квадратичного отношения площадей к длинам треугольников с одинаковым бесконечно малым углом в начале координат применима следующая формула:
d
d
s
aslh
(
s
)
=
[
d
d
s
arctan
(
s
)
]
D
(
s
)
2
=
1
s
2
+
1
D
(
s
)
2
=
1
s
2
+
1
(
s
2
+
1
s
4
+
1
4
)
2
=
1
s
4
+
1
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^{4}+1}}}}
На изображении, касательно площади lemniscatus Hyperbolicus, высота пересечения диагонали и изогнутой линии соответствует удвоенной зеленой области. Сама зеленая область создается как разностный интеграл функции суперэллипса от нуля до соответствующего значения высоты за вычетом площади соседнего треугольника:
atlh
(
v
)
=
2
(
∫
0
v
1
−
w
4
4
d
w
)
−
v
1
−
v
4
4
{\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}}
d
d
v
atlh
(
v
)
=
2
1
−
v
4
4
−
(
d
d
v
v
1
−
v
4
4
)
=
1
(
1
−
v
4
)
3
/
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}}-{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}}}
Применяется следующее преобразование:
aslh
(
x
)
=
atlh
(
x
x
4
+
1
4
)
{\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}}
Итак, согласно правилу цепочки , этот вывод имеет место:
d
d
x
aslh
(
x
)
=
d
d
x
atlh
(
x
x
4
+
1
4
)
=
(
d
d
x
x
x
4
+
1
4
)
[
1
−
(
x
x
4
+
1
4
)
4
]
−
3
/
4
=
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=}
=
1
(
x
4
+
1
)
5
/
4
[
1
−
(
x
x
4
+
1
4
)
4
]
−
3
/
4
=
1
(
x
4
+
1
)
5
/
4
(
1
x
4
+
1
)
−
3
/
4
=
1
x
4
+
1
{\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{-3/4}={\frac {1}{\sqrt {x^{4}+1}}}}
В этом списке точно показаны значения гиперболического лемнискатного синуса . Напомним,
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
ϖ
2
=
σ
2
=
1.85407
…
{\displaystyle \int _{0}^{\infty }{\frac {\operatorname {d} t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\varpi }{\sqrt {2}}}={\frac {\sigma }{2}}=1.85407\ldots }
тогда как
1
2
B
(
1
2
,
1
2
)
=
π
2
,
{\displaystyle {\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}={\tfrac {\pi }{2}},}
slh
(
ϖ
2
2
)
=
slh
(
σ
4
)
=
1
{\displaystyle {\operatorname {slh} }{\bigl (}{\tfrac {\varpi }{2{\sqrt {2}}}}{\bigr )}={\operatorname {slh} }{\bigl (}{\tfrac {\sigma }{4}}{\bigr )}=1}
sin
(
π
2
)
=
1
{\displaystyle {\sin }{\bigl (}{\tfrac {\pi }{2}}{\bigr )}=1}
slh
(
ϖ
2
2
)
=
1
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{2{\sqrt {2}}}}\right)=1}
slh
(
ϖ
3
2
)
=
1
3
4
2
3
−
3
4
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}}
slh
(
2
ϖ
3
2
)
=
2
3
+
3
4
{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt {3}}+3}}}
slh
(
ϖ
4
2
)
=
1
2
4
(
2
+
1
−
1
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}-1)}
slh
(
3
ϖ
4
2
)
=
1
2
4
(
2
+
1
+
1
)
{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}+1)}
slh
(
ϖ
5
2
)
=
1
8
4
5
−
1
20
4
−
5
+
1
=
2
5
−
2
4
sin
(
1
20
π
)
sin
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}
slh
(
2
ϖ
5
2
)
=
1
2
2
4
(
5
+
1
)
20
4
−
5
+
1
=
2
5
+
2
4
sin
(
1
20
π
)
sin
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}
slh
(
3
ϖ
5
2
)
=
1
8
4
5
−
1
20
4
+
5
+
1
=
2
5
−
2
4
cos
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
slh
(
4
ϖ
5
2
)
=
1
2
2
4
(
5
+
1
)
20
4
+
5
+
1
=
2
5
+
2
4
cos
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
slh
(
ϖ
6
2
)
=
1
2
(
2
3
+
3
+
1
)
(
1
−
2
3
−
3
4
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1-{\sqrt[{4}]{2{\sqrt {3}}-3}})}
slh
(
5
ϖ
6
2
)
=
1
2
(
2
3
+
3
+
1
)
(
1
+
2
3
−
3
4
)
{\displaystyle \operatorname {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}
В этой таблице показаны наиболее важные значения функций гиперболического лемнискатного тангенса и котангенса :
z
{\displaystyle z}
clh
z
{\displaystyle \operatorname {clh} z}
slh
z
{\displaystyle \operatorname {slh} z}
ctlh
z
=
cos
4
z
{\displaystyle \operatorname {ctlh} z=\cos _{4}z}
tlh
z
=
sin
4
z
{\displaystyle \operatorname {tlh} z=\sin _{4}z}
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
1
{\displaystyle 1}
0
{\displaystyle 0}
1
4
σ
{\displaystyle {\tfrac {1}{4}}\sigma }
1
{\displaystyle 1}
1
{\displaystyle 1}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
1
2
σ
{\displaystyle {\tfrac {1}{2}}\sigma }
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
1
{\displaystyle 1}
3
4
σ
{\displaystyle {\tfrac {3}{4}}\sigma }
−
1
{\displaystyle -1}
−
1
{\displaystyle -1}
−
1
/
2
4
{\displaystyle -1{\big /}{\sqrt[{4}]{2}}}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
σ
{\displaystyle \sigma }
∞
{\displaystyle \infty }
0
{\displaystyle 0}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
В сочетании с гиперболическим лемнискатным ареазином можно установить следующие тождества:
tlh
[
aslh
(
x
)
]
=
ctlh
[
aclh
(
x
)
]
=
x
x
4
+
1
4
{\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}}
ctlh
[
aslh
(
x
)
]
=
tlh
[
aclh
(
x
)
]
=
1
x
4
+
1
4
{\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}}
Квадрат касательной гиперболической лемнискаты является пифагорейским аналогом квадрата котангенса гиперболической лемнискаты, поскольку сумма четвертых степеней
tlh
{\displaystyle \operatorname {tlh} }
ctlh
{\displaystyle \operatorname {ctlh} }
Теорема о биссектрисе гиперболического синуса lemniscatus гласит:
slh
[
1
2
aslh
(
x
)
]
=
2
x
x
2
+
1
+
x
4
+
1
+
x
4
+
1
−
x
2
+
1
{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2}}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}}
Эту формулу можно представить как комбинацию следующих двух формул:
a
s
l
h
(
x
)
=
2
arcsl
[
x
(
x
4
+
1
+
1
)
−
1
/
2
]
{\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}
arcsl
(
x
)
=
2
aslh
(
2
x
1
+
x
2
+
1
−
x
2
)
{\displaystyle {\text{arcsl}}(x)={\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}}
Кроме того, следующие формулы действительны для всех действительных значений
x
∈
R
{\displaystyle x\in \mathbb {R} }
slh
[
1
2
aclh
(
x
)
]
=
x
4
+
1
+
x
2
−
2
x
x
4
+
1
+
x
2
=
(
x
4
+
1
−
x
2
+
1
)
−
1
/
2
(
x
4
+
1
+
1
−
x
)
{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}
clh
[
1
2
aclh
(
x
)
]
=
x
4
+
1
+
x
2
+
2
x
x
4
+
1
+
x
2
=
(
x
4
+
1
−
x
2
+
1
)
−
1
/
2
(
x
4
+
1
+
1
+
x
)
{\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}
Эти тождества следуют из последней упомянутой формулы:
tlh
[
1
2
aclh
(
x
)
]
2
=
1
2
2
−
2
2
x
x
4
+
1
−
x
2
=
(
2
x
2
+
2
+
2
x
4
+
1
)
−
1
/
2
(
x
4
+
1
+
1
−
x
)
{\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}
ctlh
[
1
2
aclh
(
x
)
]
2
=
1
2
2
+
2
2
x
x
4
+
1
−
x
2
=
(
2
x
2
+
2
+
2
x
4
+
1
)
−
1
/
2
(
x
4
+
1
+
1
+
x
)
{\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}
Следующие формулы для лемнискатического синуса и лемнискатического косинуса тесно связаны между собой:
sl
[
1
2
2
aclh
(
x
)
]
=
cl
[
1
2
2
aslh
(
x
)
]
=
x
4
+
1
−
x
2
{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}
sl
[
1
2
2
aslh
(
x
)
]
=
cl
[
1
2
2
aclh
(
x
)
]
=
x
(
x
4
+
1
+
1
)
−
1
/
2
{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]=x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}}
Аналогично определению несобственного интеграла в функции колоколообразной кривой Гаусса , преобразование координат общего цилиндра можно использовать для вычисления интеграла от 0 до положительной бесконечности в функции
f
(
x
)
=
exp
(
−
x
4
)
{\displaystyle f(x)=\exp(-x^{4})}
Это преобразование цилиндрических координат в функции колоколообразной кривой Гаусса:
[
∫
0
∞
exp
(
−
x
2
)
d
x
]
2
=
∫
0
∞
∫
0
∞
exp
(
−
y
2
−
z
2
)
d
y
d
z
=
{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{2}-z^{2})\,\mathrm {d} y\,\mathrm {d} z=}
=
∫
0
π
/
2
∫
0
∞
det
[
∂
/
∂
r
r
cos
(
ϕ
)
∂
/
∂
ϕ
r
cos
(
ϕ
)
∂
/
∂
r
r
sin
(
ϕ
)
∂
/
∂
ϕ
r
sin
(
ϕ
)
]
exp
{
−
[
r
cos
(
ϕ
)
]
2
−
[
r
sin
(
ϕ
)
]
2
}
d
r
d
ϕ
=
{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos(\phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}
=
∫
0
π
/
2
∫
0
∞
r
exp
(
−
r
2
)
d
r
d
ϕ
=
∫
0
π
/
2
1
2
d
ϕ
=
π
4
{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }r\exp(-r^{2})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\pi /2}{\frac {1}{2}}\,\mathrm {d} \phi ={\frac {\pi }{4}}}
А это аналогичное преобразование координат для лемнискатного случая:
[
∫
0
∞
exp
(
−
x
4
)
d
x
]
2
=
∫
0
∞
∫
0
∞
exp
(
−
y
4
−
z
4
)
d
y
d
z
=
{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{4}-z^{4})\,\mathrm {d} y\,\mathrm {d} z=}
=
∫
0
ϖ
/
2
∫
0
∞
det
[
∂
/
∂
r
r
ctlh
(
ϕ
)
∂
/
∂
ϕ
r
ctlh
(
ϕ
)
∂
/
∂
r
r
tlh
(
ϕ
)
∂
/
∂
ϕ
r
tlh
(
ϕ
)
]
exp
{
−
[
r
ctlh
(
ϕ
)
]
4
−
[
r
tlh
(
ϕ
)
]
4
}
d
r
d
ϕ
=
{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\,{\text{ctlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{tlh}}(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}
=
∫
0
ϖ
/
2
∫
0
∞
r
exp
(
−
r
4
)
d
r
d
ϕ
=
∫
0
ϖ
/
2
π
4
d
ϕ
=
ϖ
π
4
2
{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }r\exp(-r^{4})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\varpi /{\sqrt {2}}}{\frac {\sqrt {\pi }}{4}}\,\mathrm {d} \phi ={\frac {\varpi {\sqrt {\pi }}}{4{\sqrt {2}}}}}
В последней строке этой эллиптически аналогичной цепочки уравнений снова находится исходная колоколообразная кривая Гаусса, интегрированная с квадратичной функцией в качестве внутренней замены в соответствии с Цепным правилом инфинитезимальной аналитики (анализа).
В обоих случаях определитель матрицы Якоби умножается на исходную функцию в области интегрирования.
Полученные в результате новые функции в области интеграции затем интегрируются в соответствии с новыми параметрами.
В алгебраической теории чисел каждое конечное абелево расширение гауссовых рациональных чисел
Q
(
i
)
{\displaystyle \mathbb {Q} (i)}
подполем
Q
(
i
,
ω
n
)
{\displaystyle \mathbb {Q} (i,\omega _{n})}
n
{\displaystyle n}
[ 23 ] [ 72 ] теореме Кронекера–Вебера для рациональных чисел.
Q
{\displaystyle \mathbb {Q} }
Q
{\displaystyle \mathbb {Q} }
Q
(
ζ
n
)
{\displaystyle \mathbb {Q} (\zeta _{n})}
n
{\displaystyle n}
двенадцатой проблемой Гильберта .
Поле
Q
(
i
,
sl
(
ϖ
/
n
)
)
{\displaystyle \mathbb {Q} (i,\operatorname {sl} (\varpi /n))}
n
{\displaystyle n}
Q
(
i
)
{\displaystyle \mathbb {Q} (i)}
x
{\displaystyle x}
y
{\displaystyle y}
(
1
+
i
)
n
{\displaystyle (1+i)n}
точки кручения на эллиптической кривой
y
2
=
4
x
3
+
x
{\displaystyle y^{2}=4x^{3}+x}
[ 72 ]
Числа Бернулли
B
n
{\displaystyle \mathrm {B} _{n}}
B
n
=
lim
z
→
0
d
n
d
z
n
z
e
z
−
1
,
n
≥
0
{\displaystyle \mathrm {B} _{n}=\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}{\frac {z}{e^{z}-1}},\quad n\geq 0}
и появиться в
∑
k
∈
Z
∖
{
0
}
1
k
2
n
=
(
−
1
)
n
−
1
B
2
n
(
2
π
)
2
n
(
2
n
)
!
=
2
ζ
(
2
n
)
,
n
≥
1
{\displaystyle \sum _{k\in \mathbb {Z} \setminus \{0\}}{\frac {1}{k^{2n}}}=(-1)^{n-1}\mathrm {B} _{2n}{\frac {(2\pi )^{2n}}{(2n)!}}=2\zeta (2n),\quad n\geq 1}
где
ζ
{\displaystyle \zeta }
дзета-функция Римана .
Числа Гурвица
H
n
,
{\displaystyle \mathrm {H} _{n},}
Адольфа Гурвица , являются «лемнискатными аналогами» чисел Бернулли. Они могут быть определены по [ 73 ] [ 74 ]
H
n
=
−
lim
z
→
0
d
n
d
z
n
z
ζ
(
z
;
1
/
4
,
0
)
,
n
≥
0
{\displaystyle \mathrm {H} _{n}=-\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}z\zeta (z;1/4,0),\quad n\geq 0}
где
ζ
(
⋅
;
1
/
4
,
0
)
{\displaystyle \zeta (\cdot ;1/4,0)}
дзета-функция Вейерштрасса с инвариантами решетки
1
/
4
{\displaystyle 1/4}
0
{\displaystyle 0}
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
n
=
H
4
n
(
2
ϖ
)
4
n
(
4
n
)
!
=
G
4
n
(
i
)
,
n
≥
1
{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4n}}}=\mathrm {H} _{4n}{\frac {(2\varpi )^{4n}}{(4n)!}}=G_{4n}(i),\quad n\geq 1}
где
Z
[
i
]
{\displaystyle \mathbb {Z} [i]}
гауссовскими целыми числами и
G
4
n
{\displaystyle G_{4n}}
ряд Эйзенштейна по весу
4
n
{\displaystyle 4n}
∑
n
=
1
∞
n
k
e
2
π
n
−
1
=
{
1
24
−
1
8
π
if
k
=
1
B
k
+
1
2
k
+
2
if
k
≡
1
(
m
o
d
4
)
and
k
≥
5
B
k
+
1
2
k
+
2
+
H
k
+
1
2
k
+
2
(
ϖ
π
)
k
+
1
if
k
≡
3
(
m
o
d
4
)
and
k
≥
3.
{\displaystyle \displaystyle {\begin{array}{ll}\displaystyle \sum _{n=1}^{\infty }{\dfrac {n^{k}}{e^{2\pi n}-1}}={\begin{cases}{\dfrac {1}{24}}-{\dfrac {1}{8\pi }}&{\text{if}}\ k=1\\{\dfrac {\mathrm {B} _{k+1}}{2k+2}}&{\text{if}}\ k\equiv 1\,(\mathrm {mod} \,4)\ {\text{and}}\ k\geq 5\\{\dfrac {\mathrm {B} _{k+1}}{2k+2}}+{\dfrac {\mathrm {H} _{k+1}}{2k+2}}\left({\dfrac {\varpi }{\pi }}\right)^{k+1}&{\text{if}}\ k\equiv 3\,(\mathrm {mod} \,4)\ {\text{and}}\ k\geq 3.\\\end{cases}}\end{array}}}
Числа Гурвица также можно определить следующим образом:
H
4
=
1
/
10
{\displaystyle \mathrm {H} _{4}=1/10}
H
4
n
=
3
(
2
n
−
3
)
(
16
n
2
−
1
)
∑
k
=
1
n
−
1
(
4
n
4
k
)
(
4
k
−
1
)
(
4
(
n
−
k
)
−
1
)
H
4
k
H
4
(
n
−
k
)
,
n
≥
2
{\displaystyle \mathrm {H} _{4n}={\frac {3}{(2n-3)(16n^{2}-1)}}\sum _{k=1}^{n-1}{\binom {4n}{4k}}(4k-1)(4(n-k)-1)\mathrm {H} _{4k}\mathrm {H} _{4(n-k)},\quad n\geq 2}
и
H
n
=
0
{\displaystyle \mathrm {H} _{n}=0}
n
{\displaystyle n}
4
{\displaystyle 4}
[ 75 ] [ 73 ]
H
8
=
3
10
,
H
12
=
567
130
,
H
16
=
43
659
170
,
…
{\displaystyle \mathrm {H} _{8}={\frac {3}{10}},\,\mathrm {H} _{12}={\frac {567}{130}},\,\mathrm {H} _{16}={\frac {43\,659}{170}},\,\ldots }
Также [ 76 ]
denom
H
4
n
=
2
∏
(
p
−
1
)
|
4
n
p
{\displaystyle \operatorname {denom} \mathrm {H} _{4n}=2\prod _{(p-1)|4n}p}
где
p
∈
P
{\displaystyle p\in \mathbb {P} }
p
≡
1
(
mod
4
)
,
{\displaystyle p\equiv 1\,({\text{mod}}\,4),}
denom
B
2
n
=
∏
(
p
−
1
)
|
2
n
p
{\displaystyle \operatorname {denom} \mathrm {B} _{2n}=\prod _{(p-1)|2n}p}
где
p
∈
P
{\displaystyle p\in \mathbb {P} }
теореме фон Штаудта–Клаузена ).
Фактически, теорема фон Штаудта – Клаузена утверждает, что
B
2
n
+
∑
(
p
−
1
)
|
2
n
1
p
∈
Z
,
n
≥
1
{\displaystyle \mathrm {B} _{2n}+\sum _{(p-1)|2n}{\frac {1}{p}}\in \mathbb {Z} ,\quad n\geq 1}
(последовательность A000146 OEIS ), где
p
{\displaystyle p}
a
∈
Z
{\displaystyle a\in \mathbb {Z} }
b
∈
Z
{\displaystyle b\in \mathbb {Z} }
p
{\displaystyle p}
p
≡
1
(
m
o
d
4
)
{\displaystyle p\equiv 1\,(\mathrm {mod} \,4)}
p
=
a
2
+
b
2
{\displaystyle p=a^{2}+b^{2}}
теорему Ферма о суммах двух квадратов ) и
a
≡
b
+
1
(
m
o
d
4
)
{\displaystyle a\equiv b+1\,(\mathrm {mod} \,4)}
p
{\displaystyle p}
a
=
a
p
{\displaystyle a=a_{p}}
[ 73 ]
H
4
n
−
1
2
−
∑
(
p
−
1
)
|
4
n
(
2
a
p
)
4
n
/
(
p
−
1
)
p
=
def
G
n
∈
Z
,
n
≥
1
,
{\displaystyle \mathrm {H} _{4n}-{\frac {1}{2}}-\sum _{(p-1)|4n}{\frac {(2a_{p})^{4n/(p-1)}}{p}}\mathrel {\overset {\text{def}}{=}} \mathrm {G} _{n}\in \mathbb {Z} ,\quad n\geq 1,}
sl
z
=
∑
n
=
0
∞
k
4
n
+
1
z
4
n
+
1
(
4
n
+
1
)
!
,
|
z
|
<
ϖ
2
⟹
k
p
≡
2
a
p
(
mod
p
)
.
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }k_{4n+1}{\frac {z^{4n+1}}{(4n+1)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}\implies k_{p}\equiv 2a_{p}\,({\text{mod}}\,p).}
Последовательность целых чисел
G
n
{\displaystyle \mathrm {G} _{n}}
0
,
−
1
,
5
,
253
,
…
.
{\displaystyle 0,-1,5,253,\ldots .}
[ 73 ]
Позволять
n
≥
2
{\displaystyle n\geq 2}
4
n
+
1
{\displaystyle 4n+1}
G
n
≡
1
(
m
o
d
4
)
{\displaystyle \mathrm {G} _{n}\equiv 1\,(\mathrm {mod} \,4)}
4
n
+
1
{\displaystyle 4n+1}
G
n
≡
3
(
m
o
d
4
)
{\displaystyle \mathrm {G} _{n}\equiv 3\,(\mathrm {mod} \,4)}
[ 77 ]
Вместо этого некоторые авторы определяют числа Гурвица как
H
n
′
=
H
4
n
{\displaystyle \mathrm {H} _{n}'=\mathrm {H} _{4n}}
Числа Гурвица появляются в нескольких разложениях рядов Лорана, связанных с функциями лемнискат: [ 78 ]
sl
2
z
=
∑
n
=
1
∞
2
4
n
(
1
−
(
−
1
)
n
2
2
n
)
H
4
n
4
n
z
4
n
−
2
(
4
n
−
2
)
!
,
|
z
|
<
ϖ
2
sl
′
z
sl
z
=
1
z
−
∑
n
=
1
∞
2
4
n
(
2
−
(
−
1
)
n
2
2
n
)
H
4
n
4
n
z
4
n
−
1
(
4
n
−
1
)
!
,
|
z
|
<
ϖ
2
1
sl
z
=
1
z
−
∑
n
=
1
∞
2
2
n
(
(
−
1
)
n
2
−
2
2
n
)
H
4
n
4
n
z
4
n
−
1
(
4
n
−
1
)
!
,
|
z
|
<
ϖ
1
sl
2
z
=
1
z
2
+
∑
n
=
1
∞
2
4
n
H
4
n
4
n
z
4
n
−
2
(
4
n
−
2
)
!
,
|
z
|
<
ϖ
{\displaystyle {\begin{aligned}\operatorname {sl} ^{2}z&=\sum _{n=1}^{\infty }{\frac {2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-2}}{(4n-2)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}\\{\frac {\operatorname {sl} 'z}{\operatorname {sl} {z}}}&={\frac {1}{z}}-\sum _{n=1}^{\infty }{\frac {2^{4n}(2-(-1)^{n}2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-1}}{(4n-1)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}\\{\frac {1}{\operatorname {sl} z}}&={\frac {1}{z}}-\sum _{n=1}^{\infty }{\frac {2^{2n}((-1)^{n}2-2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-1}}{(4n-1)!}},\quad \left|z\right|<\varpi \\{\frac {1}{\operatorname {sl} ^{2}z}}&={\frac {1}{z^{2}}}+\sum _{n=1}^{\infty }{\frac {2^{4n}\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-2}}{(4n-2)!}},\quad \left|z\right|<\varpi \end{aligned}}}
Аналогично, в терминах чисел Бернулли:
1
sinh
2
z
=
1
z
2
−
∑
n
=
1
∞
2
2
n
B
2
n
2
n
z
2
n
−
2
(
2
n
−
2
)
!
,
|
z
|
<
π
.
{\displaystyle {\frac {1}{\sinh ^{2}z}}={\frac {1}{z^{2}}}-\sum _{n=1}^{\infty }{\frac {2^{2n}\mathrm {B} _{2n}}{2n}}{\frac {z^{2n-2}}{(2n-2)!}},\quad \left|z\right|<\pi .}
Позволять
p
{\displaystyle p}
p
≡
1
(
mod
4
)
{\displaystyle p\equiv 1\,({\text{mod}}\,4)}
остаток (мод.
p
{\displaystyle p}
(
a
p
)
4
{\displaystyle \left({\tfrac {a}{p}}\right)_{4}}
1
{\displaystyle 1}
a
{\displaystyle a}
p
{\displaystyle p}
−
1
{\displaystyle -1}
a
{\displaystyle a}
p
{\displaystyle p}
Если
a
{\displaystyle a}
p
{\displaystyle p}
p
′
∈
Z
[
i
]
{\displaystyle p'\in \mathbb {Z} [i]}
[ 79 ] [ 80 ]
(
a
p
)
4
=
∏
p
′
sl
(
2
ϖ
a
p
′
/
p
)
sl
(
2
ϖ
p
′
/
p
)
.
{\displaystyle \left({\frac {a}{p}}\right)_{4}=\prod _{p'}{\frac {\operatorname {sl} (2\varpi ap'/p)}{\operatorname {sl} (2\varpi p'/p)}}.}
Эта теорема аналогична
(
a
p
)
=
∏
n
=
1
p
−
1
2
sin
(
2
π
a
n
/
p
)
sin
(
2
π
n
/
p
)
{\displaystyle \left({\frac {a}{p}}\right)=\prod _{n=1}^{\frac {p-1}{2}}{\frac {\sin(2\pi an/p)}{\sin(2\pi n/p)}}}
где
(
⋅
⋅
)
{\displaystyle \left({\tfrac {\cdot }{\cdot }}\right)}
символ Лежандра .
«Мир в квинкунциальной проекции» Пирса (1879) . , Квинкунциальная проекция Пирса разработанная Чарльзом Сандерсом Пирсом из Службы береговой службы США в 1870-х годах, представляет собой картографическую проекцию мира , основанную на обратном лемнискате синуса стереографически проецируемых точек (рассматриваемых как комплексные числа). [ 81 ]
Когда линии постоянной действительной или мнимой части проецируются на комплексную плоскость через гиперболический лемнискатный синус, а затем стереографически проецируются на сферу (см. Сфера Римана ), полученные кривые представляют собой сферические коники , сферический аналог плоских эллипсов и гипербол . [ 82 ] эллиптические функции Якоби ) обеспечивают параметризацию сферических коник.
Конформная картографическая проекция глобуса на 6 квадратных граней куба также может быть определена с помощью функций лемнискаты. [ 83 ] уравнения в частных производных можно эффективно решить с помощью конформного отображения, такое отображение сферы в куб удобно для моделирования атмосферы . [ 84 ]
^ Фаньяно (1718–1723) ; Эйлер (1761 г.) ; Гаусс (1917) ^ Гаусс (1917) с. 199 использовали символы sl и cl для обозначения лемнискатного синуса и косинуса соответственно, и это обозначение наиболее распространено сегодня: см., например, Cox (1984), с. 316, Эймар и Лафон (2004), с. 204, и Леммермейер (2000), с. 240. Аюб (1984) использует синлем и кослем . Уиттакер и Уотсон (1920) используют символы sin lemn и cos lemn . В некоторых источниках используются общие буквы s c Прасолов и Соловьев (1997) используют букву φ φ' ^ Круг
x
2
+
y
2
=
x
{\displaystyle x^{2}+y^{2}=x}
(
1
2
,
0
)
{\textstyle {\bigl (}{\tfrac {1}{2}},0{\bigr )}}
r
=
cos
θ
,
{\displaystyle r=\cos \theta ,}
клевер по определению Кокса и Шурмана (2005) . Это не единичного радиуса круг
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}}
^ Основные периоды
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
^ Робинсон (2019a) исходит из этого определения и отсюда выводит другие свойства лемнискатных функций. ^ Эта карта была первым изображением отображения Шварца – Кристоффеля в книге Шварца (1869), с. 113 .
^ Шаппахер (1997) . Последовательность OEIS A062539 перечисляет десятичные цифры константы лемнискаты. ^ Левин (2006) ^ Тодд (1975) ^ Кокс (1984) ^ Темные области представляют собой нули, а светлые области представляют собой полюса. В аргумента качестве
sl
z
{\displaystyle \operatorname {sl} z}
−
π
{\displaystyle -\pi }
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
Arg
≈
0
)
{\displaystyle (\operatorname {Arg} \approx 0)}
(
Arg
≈
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx \pi /2)}
(
Arg
≈
π
)
{\displaystyle (\operatorname {Arg} \approx \pi )}
^ Объединение первого и четвертого тождества дает
sl
z
=
−
i
/
sl
(
z
−
(
1
+
i
)
ϖ
/
2
)
{\displaystyle \operatorname {sl} z=-i/\operatorname {sl} (z-(1+i)\varpi /2)}
Eymard & Lafon (2004), с. 226, без знака минус спереди справа.
^ Чётные гауссовы целые числа — это класс вычетов 0 по модулю 1 + i , чёрные квадраты на шахматной доске .
↑ Prasolov & Solovyev (1997) ; Robinson (2019a) ^ Перейти обратно: а б Кокс (2012) ^ Рейнхардт и Уокер (2010a) §22.12.6 , §22.12.12 ^ Аналогично,
1
sin
z
=
∑
n
∈
Z
(
−
1
)
n
z
+
n
π
.
{\displaystyle {\frac {1}{\sin z}}=\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{z+n\pi }}.}
^ Линдквист и Пеэтре (2001) обобщают первую из этих форм. ^ Ayoub (1984) ; Prasolov & Solovyev (1997) ^ Эйлер (1761) §44 с. 79 , §47 стр. 80–81 ^ Перейти обратно: а б Эйлер (1761) §46 с. 80 ^ На самом деле,
i
ε
=
sl
β
ϖ
2
{\displaystyle i^{\varepsilon }=\operatorname {sl} {\tfrac {\beta \varpi }{2}}}
^ Перейти обратно: а б с Кокс и Хайд (2014) ^ Гомес-Молледа и Ларио (2019) ^ четвертый корень с наименьшим положительным главным аргументом . Выбирается
^ Ограничение на положительные и нечетные
β
{\displaystyle \beta }
deg
Λ
β
=
|
(
O
/
β
O
)
×
|
{\displaystyle \operatorname {deg} \Lambda _{\beta }=\left|({\mathcal {O}}/\beta {\mathcal {O}})^{\times }\right|}
^ Кокс (2013) с. 142, пример 7.29(в) ^ Розен (1981) ^ Эймар и Лафон (2004), с. 200 ^ Эйлер (1761) ; Сигел (1969) . Прасолов и Соловьев (1997) используют представление лемнискаты в полярных координатах для определения дифференциальной длины дуги, но результат тот же. ^ Рейнхардт и Уокер (2010a) §22.18.E6 ^ Сигел (1969) ; Шаппахер (1997) ^ Такие номера представляют собой последовательность OEIS A003401 .
↑ Abel (1827–1828) ; Rosen (1981) ; Prasolov & Solovyev (1997) ^ Эйлер (1786) ; Шридхаран (2004) ; Левиен (2008) ^ «А104203» . Электронная энциклопедия целочисленных последовательностей . ^ Ломонт, Дж.С.; Бриллхарт, Джон (2001). Эллиптические полиномы . ЦРК Пресс. стр. 12, 44. ISBN. 1-58488-210-7 ^ Перейти обратно: а б с д «А193543 — Оайс» . ^ Ломонт, Дж.С.; Бриллхарт, Джон (2001). Эллиптические полиномы . ЦРК Пресс. ISBN 1-58488-210-7 ^ Ломонт, Дж.С.; Бриллхарт, Джон (2001). Эллиптические полиномы . ЦРК Пресс. ISBN 1-58488-210-7 ^ Перейти обратно: а б «А289695 — Оайс» . ^ Уолл, HS (1948). Аналитическая теория цепных дробей . Издательская компания Челси. стр. 374–375. ^ Рейнхардт и Уокер (2010a) §22.20(ii) ^ Карлсон (2010) §19.8 ^ Дикманн, Андреас. «Коллекция бесконечных произведений и серий» . ^ Рейнхардт и Уокер (2010a) §22.12.12 ; Вигрен и Дикманн (2020), с. 7 ^ В общем,
sinh
(
x
−
n
π
)
{\displaystyle \sinh(x-n\pi )}
sin
(
x
−
n
π
i
)
=
−
i
sinh
(
i
x
+
n
π
)
{\displaystyle \sin(x-n\pi i)=-i\sinh(ix+n\pi )}
^ Рейнхардт и Уокер (2010a) §22.11 ^ Рейнхардт и Уокер (2010a) §22.2.E7 ^ Берндт (1994) с. 247, 248, 253 ^ Рейнхардт и Уокер (2010a) §22.11.E1 ^ Уиттакер и Ватсон (1927) ^ Борвейн и Борвейн (1987) ^ Перейти обратно: а б Эймар и Лафон (2004), с. 227. ^ Картан, Х. (1961). Элементарная теория аналитических функций одной или нескольких комплексных переменных (на французском языке). Германн. стр. 160–164. ^ Точнее, предположим
{
a
n
}
{\displaystyle \{a_{n}\}}
S
{\displaystyle S}
∑
|
a
n
(
z
)
|
{\textstyle \sum \left|a_{n}(z)\right|}
S
{\displaystyle S}
{
n
1
,
n
2
,
n
3
,
…
}
{\displaystyle \{n_{1},n_{2},n_{3},\ldots \}}
перестановка любая
{
1
,
2
,
3
,
…
}
{\displaystyle \{1,2,3,\ldots \}}
∏
n
=
1
∞
(
1
+
a
n
(
z
)
)
=
∏
k
=
1
∞
(
1
+
a
n
k
(
z
)
)
{\textstyle \prod _{n=1}^{\infty }(1+a_{n}(z))=\prod _{k=1}^{\infty }(1+a_{n_{k}}(z))}
z
∈
S
{\displaystyle z\in S}
биекция между натуральными числами и
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
^ Боттаццини и Грей (2013), с. 58 ^ Точнее, если для каждого
k
{\displaystyle k}
lim
n
→
∞
a
k
(
n
)
{\textstyle \lim _{n\to \infty }a_{k}(n)}
∑
k
=
1
∞
M
k
{\textstyle \sum _{k=1}^{\infty }M_{k}}
|
a
k
(
n
)
|
≤
M
k
{\displaystyle \left|a_{k}(n)\right|\leq M_{k}}
n
∈
N
{\displaystyle n\in \mathbb {N} }
1
≤
k
≤
n
{\displaystyle 1\leq k\leq n}
lim
n
→
∞
∑
k
=
1
n
a
k
(
n
)
=
∑
k
=
1
∞
lim
n
→
∞
a
k
(
n
)
.
{\displaystyle \lim _{n\to \infty }\sum _{k=1}^{n}a_{k}(n)=\sum _{k=1}^{\infty }\lim _{n\to \infty }a_{k}(n).}
^ Альтернативно можно сделать вывод, что эти разложения существуют только из аналитичности
M
{\displaystyle M}
N
{\displaystyle N}
∑
α
1
α
4
=
−
the coefficient of
z
5
{\textstyle \sum _{\alpha }{\frac {1}{\alpha ^{4}}}=-\,{\text{the coefficient of}}\,z^{5}}
M
{\displaystyle M}
^ Гаусс, CF (1866). Сочинения (Том III)
φ
17
{\displaystyle \varphi ^{17}}
107
7
410
154
752
000
{\displaystyle {\tfrac {107}{7\,410\,154\,752\,000}}}
107
207
484
333
056
000
{\displaystyle {\tfrac {107}{207\,484\,333\,056\,000}}}
^
M
{\displaystyle M}
M
(
z
)
M
⁗
(
z
)
−
4
M
′
(
z
)
M
‴
(
z
)
+
{\displaystyle M(z)M''''(z)-4M'(z)M'''(z)+}
+
3
M
″
(
z
)
2
−
2
M
(
z
)
2
=
0
{\displaystyle +3M''(z)^{2}-2M(z)^{2}=0}
N
{\displaystyle N}
(
N
″
(
z
)
N
(
z
)
−
N
′
(
z
)
2
)
2
−
M
(
z
)
4
=
0.
{\displaystyle (N''(z)N(z)-N'(z)^{2})^{2}-M(z)^{4}=0.}
^ Если
M
(
z
)
=
∑
n
=
0
∞
a
n
z
n
+
1
{\textstyle M(z)=\sum _{n=0}^{\infty }a_{n}z^{n+1}}
a
n
{\displaystyle a_{n}}
a
n
+
1
=
−
1
n
+
1
∑
k
=
0
n
2
n
−
k
+
1
a
k
H
n
−
k
+
1
(
n
−
k
+
1
)
!
{\textstyle a_{n+1}=-{\frac {1}{n+1}}\sum _{k=0}^{n}2^{n-k+1}a_{k}{\frac {\mathrm {H} _{n-k+1}}{(n-k+1)!}}}
a
0
=
1
{\displaystyle a_{0}=1}
H
n
{\displaystyle \mathrm {H} _{n}}
эллиптических функциях Лемнискаты § числа Гурвица .
^ Zhuravskiy, A. M. (1941). Spravochnik po ellipticheskim funktsiyam (in Russian). Izd. Akad. Nauk. U.S.S.R. ^ Робинсон (2019a) ^ Эймар и Лафон (2004), с. 234 ^ Армитидж, СП; Эберлейн, ВФ (2006). Эллиптические функции . Издательство Кембриджского университета. п. 49. ИСБН 978-0-521-78563-1 ^ Личность
cl
z
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
Гринхилла (1892), с. 33 .
^ http://oeis.org/A175576 [ только URL ^ Берндт, Брюс К. (1989). Записные книжки Рамануджана, часть II . Спрингер. ISBN 978-1-4612-4530-8 ^ Левин (2006) ; Робинсон (2019б) ^ Левин (2006) с. 515 ^ Перейти обратно: а б Кокс (2012) с. 508, 509 ^ Перейти обратно: а б с д Аракава, Цунео; Ибукияма, Томойоши; Числа и дзета-функции . Бернулли 978-4-431-54918-5 ^ Эквивалентно,
H
n
=
−
lim
z
→
0
d
n
d
z
n
(
(
1
+
i
)
z
/
2
sl
(
(
1
+
i
)
z
/
2
)
+
z
2
E
(
z
2
;
i
)
)
{\displaystyle \mathrm {H} _{n}=-\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}\left({\frac {(1+i)z/2}{\operatorname {sl} ((1+i)z/2)}}+{\frac {z}{2}}{\mathcal {E}}\left({\frac {z}{2}};i\right)\right)}
n
≥
4
{\displaystyle n\geq 4}
E
(
⋅
;
i
)
{\displaystyle {\mathcal {E}}(\cdot ;i)}
эпсилон-функция Якоби с модулем
i
{\displaystyle i}
^ Числа Бернулли можно определить с помощью аналогичной рекуррентности:
B
2
n
=
−
1
2
n
+
1
∑
k
=
1
n
−
1
(
2
n
2
k
)
B
2
k
B
2
(
n
−
k
)
{\displaystyle \mathrm {B} _{2n}=-{\frac {1}{2n+1}}\sum _{k=1}^{n-1}{\binom {2n}{2k}}\mathrm {B} _{2k}\mathrm {B} _{2(n-k)}}
n
≥
2
{\displaystyle n\geq 2}
B
2
=
1
/
6
{\displaystyle \mathrm {B} _{2}=1/6}
^ Кац, Николас М. (1975). «Сравнения Клаузена — фон Штаудта и Куммера для чисел Бернулли-Гурвица» . Математические летописи . 216 (1): 1–4. ^ Гурвиц, Адольф (1963). Математические труды: Том II (на немецком языке). Шпрингер Базель АГ. ^ Аракава и др. (2014) определить
H
4
n
{\displaystyle \mathrm {H} _{4n}}
1
/
sl
2
.
{\displaystyle 1/\operatorname {sl} ^{2}.}
^ Эйзенштейн, Г. (1846). «Вклад в теорию эллиптических функций» . Журнал чистой и прикладной математики (на немецком языке). 30 .
φ
=
sl
{\displaystyle \varphi =\operatorname {sl} }
ω
=
2
ϖ
{\displaystyle \omega =2\varpi }
^ Огава, Такума (2005). «Сходства между тригонометрической функцией и функцией лемнискаты с точки зрения арифметики» . Математический журнал Цукуба . 29 (1). ^ Пирс (1879) . Гую (1887) и Адамс (1925) ввели соответственно поперечный и косой аспекты одной и той же проекции. См. также Ли (1976) . Эти авторы записывают свои формулы проекции в терминах эллиптических функций Якоби с квадратной решеткой. ^ Адамс (1925) ^ Адамс (1925) ; Ли (1976) . ^ Ранчич, Персер и Мезингер (1996) ; МакГрегор (2005) .
Абель, Нильс Хенрик (1827–1828) «Исследование эллиптических функций» (на французском языке). Журнал Крелля Часть 1 . 1827. 2 (2): 101–181. дои : 10.1515/crll.1827.2.101 . Часть 2 . 1828. 3 (3): 160–190. дои : 10.1515/crll.1828.3.160 . Адамс, Оскар Шерман (1925). Эллиптические функции, примененные к конформным картам мира (PDF) . Типография правительства США. Аюб, Раймонд (1984). «Вклад лемнискаты и Фаньяно в эллиптические интегралы». Архив истории точных наук . 29 (2): 131–149. дои : 10.1007/BF00348244 . Берндт, Брюс К. (1994). Записные книжки Рамануджана, часть IV (первое изд.). Спрингер. ISBN 978-1-4612-6932-8 Борвейн, Джонатам М .; Борвейн, Питер Б. (1987). «2.7 Преобразование Ландена». Пи и годовое общее собрание . Уайли-Интерсайенс. п. 60. Боттаццини, Умберто ; Грей, Джереми (2013). Скрытая гармония – геометрические фантазии: возникновение теории комплексных функций . Спрингер. дои : 10.1007/978-1-4614-5725-1 . Карлсон, Билли К. (2010). «19. Эллиптические интегралы» . В Олвере, Фрэнк ; и др. (ред.). Справочник NIST по математическим функциям Кокс, Дэвид Арчибальд (январь 1984 г.). «Среднее арифметико-геометрическое Гаусса» . L'Enseignement Mathématique . 30 (2): 275–330. Кокс, Дэвид Арчибальд; Шурман, Джерри (2005). «Геометрия и теория чисел на клевере» (PDF) . Американский математический ежемесячник . 112 (8): 682–704. дои : 10.1080/00029890.2005.11920241 . Кокс, Дэвид Арчибальд (2012). «Лемниската». Теория Галуа . Уайли. стр. 463–514. дои : 10.1002/9781118218457.ch15 . Кокс, Дэвид Арчибальд (2013). Простые числа формы x 2 + 2 Кокс, Дэвид Арчибальд; Хайд, Тревор (2014). «Теория Галуа о лемнискате» (PDF) . Журнал теории чисел . 135 : 43–59. arXiv : 1208.2653 дои : 10.1016/j.jnt.2013.08.006 . Эннепер, Альфред (1890) [1-е изд. 1876 г.]. «Примечание III: Исторические заметки о геометрических применениях эллиптических интегралов». [Исторические заметки о геометрических приложениях эллиптических интегралов]. Эллиптические функции, теория и история (на немецком языке). Неберт. стр. 524–547. Эйлер, Леонард (1761). «Наблюдения о сравнении дуг необратимых кривых» . Новые комментарии Императорской Петрополитанской академии наук (на латыни) 6 : 58–84. Е 252 ( Цифры ) Эйлер, Леонард (1786). «О странных свойствах упругой кривой при уравнении
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
[Об удивительных свойствах упругих кривых, содержащихся в уравнении
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
Известия Петрополитанской Императорской Академии наук (на латыни). 1782 (2): 34–61. 605 Эймар, Пьер; Лафон, Жан-Пьер (2004). Число Пи . Перевод Уилсона, Стивена. Американское математическое общество. ISBN 0-8218-3246-8 Фаньяно, Джулио Карло (1718–1723) «Метод измерения лемнискаты». Журнал итальянских писателей (на итальянском языке). «Schediasma primo» [Часть 1]. 1718. 29 : 258–269. «Достиг первой скедиазмы» [Приложение к части 1]. 1723. 34 : 197–207. «Скедиазма по» [Часть 2]. 1718. 30 : 87–111. Фаньяно (1850 г.). «32–34. Метод измерения лемнискаты» . Математические труды, вып. 2 . Аллериги и Сегати. стр. 293–313. Цифры ) Гаусс, Карл Фридрих (1917). Сочинения (том X, раздел I) Гомес-Молледа, Массачусетс; Ларио, Джоан-К. (2019). «Конструкции линейки и циркуля равностороннего треугольника и пятиугольника в лемнискатной кривой». Математический интеллект . 41 (4): 17–21. дои : 10.1007/s00283-019-09892-w . Гринхилл, Альфред Джордж (1892). Приложения эллиптических функций Гюю, Эмиль (1887). «Новая система проекции сферы: Обобщение проекции Меркатора» [Новая система проекции сферы]. Гидрографические летописи . Серия 2 (на французском языке). 9 :16–35. Хаузель, Кристиан (1978). «Эллиптические функции и абелевы интегралы». В Дьедонне, Жан (ред.). Конспект истории математики 1700–1900 гг. II (на французском языке). Германн. стр. 1–113. Хайд, Тревор (2014). «Продукт Уоллиса на клевере» (PDF) . Американский математический ежемесячник . 121 (3): 237–243. doi : 10.4169/amer.math.monthly.121.03.237 . Кубота, Томио (1964). «Некоторые арифметические применения эллиптической функции». Журнал Крелля . 214/215 : 141–145. дои : 10.1515/crll.1964.214-215.141 . Лангер, Джоэл К.; Певец, Дэвид А. (2010). «Размышления о лемнискате Бернулли: сорок восемь граней математической жемчужины» (PDF) . Миланский математический журнал . 78 (2): 643–682. дои : 10.1007/s00032-010-0124-5 . Лангер, Джоэл К.; Певец, Дэвид А. (2011). «Лемнискатическая шахматная доска» . Форум Геометрикорум . 11 : 183–199. Лоуден, Дерек Франк (1989). Эллиптические функции и приложения . Прикладные математические науки. Том. 80. Шпрингер-Верлаг. дои : 10.1007/978-1-4757-3980-0 . Ли, LP (1976). Конформные проекции на основе эллиптических функций Картографические монографии . Том. 16. Торонто: Б.В. Гуцелл, Йоркский университет. ISBN 0-919870-16-3 «Канадскому картографу» 13 Леммермейер, Франц (2000). Законы взаимности: от Эйлера до Эйзенштейна . Спрингер. ISBN 3-540-66957-4 Левиен, Раф (2008). Эластика: математическая история (PDF) (Технический отчет). Калифорнийский университет в Беркли. UCB/EECS-2008-103. Левин, Аарон (2006). «Геометрическая интерпретация бесконечного произведения константы лемнискаты». Американский математический ежемесячник . 113 (6): 510–520. дои : 10.2307/27641976 . Линдквист, Питер; Пеэтре, Яак (2001). «Два замечательных тождества, называемые двойками, для обратных к некоторым абелевым интегралам» (PDF) . Американский математический ежемесячник . 108 (5): 403–410. дои : 10.1080/00029890.2001.11919766 . Маркушевич, Алексей Иванович (1966). Замечательные синусоидальные функции Маркушевич, Алексей Иванович (1992). Введение в классическую теорию абелевых функций . Переводы математических монографий. Том. 96. Американское математическое общество. дои : 10.1090/ммоно/096 . МакГрегор, Джон Л. (2005). C-CAM: геометрические аспекты и динамическая формулировка CSIRO Исследования атмосферы . 70. Маккин, Генри ; Молл, Виктор (1999). Эллиптические кривые: теория функций, геометрия, арифметика . Кембридж. ISBN 9780521582285 Милн-Томсон, Луи Мелвилл (1964). «16. Эллиптические функции Якоби и тэта-функции» . В Абрамовице, Милтон ; Стегун, Ирен Энн (ред.). Справочник по математическим функциям Нойман, Эдвард (2007). «О лемнискатных функциях Гаусса и лемнискатическом среднем» (PDF) . Математика Панноника . 18 (1): 77–94. Нисимура, Ре (2015). «Новые свойства функции лемниската и ее преобразование» . Журнал математического анализа и приложений . 427 (1): 460–468. дои : 10.1016/j.jmaa.2015.02.066 Огава, Такума (2005). «Сходства между тригонометрической функцией и функцией лемнискаты с точки зрения арифметики» . Математический журнал Цукуба . 29 (1). Пирс, Чарльз Сандерс (1879). «Квинкунциальная проекция сферы» . Американский журнал математики . 2 (4): 394–397. дои : 10.2307/2369491 . Попеску-Пампу, Патрик (2016). Что такое Род? . Конспект лекций по математике. Том. 2162. Спрингер. дои : 10.1007/978-3-319-42312-8 . Прасолов Виктор; Соловьев, Юрий (1997). «4. Теорема Абеля о делении лемнискаты». Эллиптические функции и эллиптические интегралы . Переводы математических монографий. Том. 170. Американское математическое общество. дои : 10.1090/ммоно/170 . Ранчич, Миодраг; Персер, Р. Джеймс; Мезингер, Федор (1996). «Глобальная модель мелководья с использованием расширенного сферического куба: гномонические и конформные координаты». Ежеквартальный журнал Королевского метеорологического общества . 122 (532): 959–982. дои : 10.1002/qj.49712253209 . Рейнхардт, Уильям П.; Уокер, Питер Л. (2010a). «22. Эллиптические функции Якобиана» . В Олвере, Фрэнк; и др. (ред.). Справочник NIST по математическим функциям Рейнхардт, Уильям П.; Уокер, Питер Л. (2010b). «23. Эллиптические и модульные функции Вейерштрасса» . В Олвере, Фрэнк; и др. (ред.). Справочник NIST по математическим функциям Робинсон, Пол Л. (2019a). «Лемнискатические функции». arXiv : 1902.08614 Робинсон, Пол Л. (2019b). «Эллиптические функции в системе первого порядка». arXiv : 1903.07147 Розен, Майкл (1981). «Теорема Абеля о лемнискате». Американский математический ежемесячник . 88 (6): 387–395. дои : 10.2307/2321821 . Рой, Ранджан (2017). Эллиптические и модульные функции от Гаусса до Дедекинда и Гекке . Издательство Кембриджского университета. п. 28. ISBN 978-1-107-15938-9 Шаппахер, Норберт (1997). «Некоторые вехи лемнискатомии» (PDF) . В Сертёзе, С. (ред.). Алгебраическая геометрия (Материалы летней школы Билкент, 7–19 августа 1995 г., Анкара, Турция). Марсель Деккер. стр. 257–290. Шнайдер, Теодор (1937). «Арифметические исследования эллиптических интегралов». Математические анналы (на немецком языке). 113 (1): 1–13. дои : 10.1007/BF01571618 . Шварц, Герман Амандус (1869). «О некоторых проблемах картографии». Журнал Крелля (на немецком языке). 70 :105-120. дои : 10.1515/crll.1869.70.105 . Сигел, Карл Людвиг (1969). «1. Эллиптические функции». Темы теории комплексных функций, Vol. Я. Уайли-Интерсайенс. стр. 1–89. ISBN 0-471-60844-0 Снейп, Джейми (2004). «Лемниската Бернулли» . Приложения эллиптических функций в классической и алгебраической геометрии (Диссертация). Университет Дарема. стр. 50–56. Саутард, Томас Х. (1964). «18. Эллиптические и родственные функции Вейерштрасса» . В Абрамовице, Милтон ; Стегун, Ирен Энн (ред.). Справочник по математическим функциям Шридхаран, Рамайенгар (2004) «От физики к математике: от Линтеарии до лемнискаты». Резонанс . «Часть I» . 9 (4): 21–29. дои : 10.1007/BF02834853 . «Часть II: Работа Гаусса и Ландена» . 9 (6): 11–20. дои : 10.1007/BF02839214 . Тодд, Джон (1975). «Лемнискатные константы» . Коммуникации АКМ . 18 (1): 14–19. дои : 10.1145/360569.360580 Вигрен, Эрик; Дикманн, Андреас (21 июня 2020 г.). «Простые решения решеточных сумм для электрических полей из-за бесконечного числа параллельных линейных зарядов» . Симметрия . 12 (6): 1040. дои : 10.3390/sym12061040 Уиттакер, Эдмунд Тейлор ; Уотсон, Джордж Невилл (1920) [1-е изд. 1902]. «22.8 Функции лемнискат» . Курс современного анализа Уиттакер, Эдмунд Тейлор ; Уотсон, Джордж Невилл (1927) [4-е изд. 1927]. «21 Тета-функция». Курс современного анализа

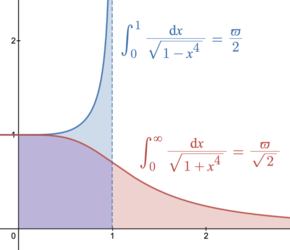






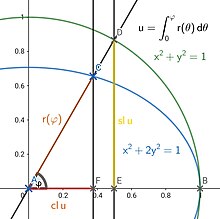


































![{\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\[6mu]\operatorname {sl} (-z)&=-\operatorname {sl} z\ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aad32bc5f3459b050ff3c535a0b2182c24c4410)


![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr)}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr ) }&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3960242e95aeb8d86d7c6666d4887c160fbac91c)



![{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi)&=\operatorname {cl} (z+i\varpi)=-\operatorname {cl} z\\[4mu]\operatorname {sl } (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4add8875fadf39f2e07fd34c565655b2e2b236)


![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+( 1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d7545373f396158c72d1b376d96364cedff009)
![{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z }}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cee565bde6b2129ca509f1e6fe214975ad634ae)












![{\displaystyle \mathbb {Z} [я]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)












![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-{\bigl (}1 +\operatorname {cl^{2}} z{\bigr )}\operatorname {sl} z=-{\frac {2\operatorname {sl} z}{\operatorname {sl} ^{2}z+1}}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\ frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&={\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\operatorname {cl} z={\frac {2\operatorname {cl} z}{\operatorname {cl} ^{2}z+1}}\\\ имя_оператора {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c432d8908a6d28872330b4474cf5c1564bf7cfd)







![{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v = {\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (uv) &=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (uv)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30e48fbafa5e12f8a952c1f0b8e279f0f9cf5fc)
![{\displaystyle {\begin{aligned}\cos(u\pm v) &=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v) &=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f19808c18b020503e6fc6074aa10141883d798)
![{\displaystyle {\begin{aligned}\operatorname {cl} (x+iy)&={\frac {\operatorname {cl} xi\operatorname {sl} x\,\operatorname {sl} y\,\operatorname { cl} y}{\operatorname {cl} y+i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {cl} x\,\operatorname {cl} y\left(1-\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}-i{\frac {\operatorname {sl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2 }x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\\[12mu]\operatorname {sl} (x+iy)&={\ frac {\operatorname {sl} x+i\operatorname {cl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} yi\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {sl} x\,\operatorname {cl} y \left(1-\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}+i{\frac {\operatorname { cl} x\,\operatorname {sl} y\left(\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^ {2}y}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f317fcc9868809494dddb639b23ec4606697f76)













![{\displaystyle {\mathcal {O}}=\mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edfff4716e70e74e7d5cd33765682964d204350a)








![{\displaystyle P_{\beta }(x),Q_{\beta }(x)\in {\mathcal {O}}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15b4185e4f3e8e88d5267f62df83d2fb3c5ac76)


![{\displaystyle \Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3324adba1f2af9b24673838187cdbe185a69d4b)



![{\displaystyle [\delta _ {\beta }]\in (1/\beta)L/L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcd7c658068f96d8253e40d98ca73fa28cc21068)




![{\displaystyle \Lambda _{\beta }(x)\in {\mathcal {O}}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96abdb3c8466ca26c4e6f40898b4d2e0415cf31)

![{\displaystyle \Phi _{k}(x)=\prod _{[a]\in (\mathbb {Z} /k\mathbb {Z})^{\times }}(x-\zeta _{k }^{а}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8960e92721c9f81175d4208b04391e3389bf0fa4)


![{\displaystyle K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9)





![{\displaystyle \omega _{5}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6252486e1b91a9d7bdff3ad78a174cb9ea5e19c3)
![{\displaystyle {\tilde {\omega }}_{5}={\sqrt[{4}]{-13-6{\sqrt {5}}+2{\sqrt {85+38{\sqrt {5 }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4a18e0684094b21749e757b9054fe4b1bad8d2)



![{\displaystyle K[x].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/455d0a9ea26acd4c13a8dc113f6ec1bce8c3ee52)











![{\displaystyle -{\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83cce63fb13a05291d0fb2671c2ab3a62f001fd3)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1- {\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c74fc1a430f5e7bb0244a281a1d4f1d0647ca67)




![{\displaystyle -{\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1- {\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce3bc2572b97070b5ca4642620aaa0552dcabf6c)
![{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e7446bf7046ae049852dbd22d5dc78e374b060)





![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}} \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({ \tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b71f8bb130fb48ab5bf0d0cb3dcfd26c827e6a7b)

![{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{ \sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}-1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52ae25f386dc661dee14e43dd108891a2d9dc43d)
![{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{ \sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}+1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df32229dfa090f41bbafb8ef91fdbc6ff2c5e0f6)

![{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1){\bigl (}{\sqrt {{\sqrt {5}}+2}}- 1{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9439c6c235f300cf2d5281aace54d0fef0255289)
![{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {3}{20}}\pi)\cos ({\tfrac {1}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01c7e40b20b6ca6e6c287c1462d16287e165d056)

![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt { 2+{\sqrt {2}}}}{\bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37780dec3f688806cfed0c5bc96b323e7b4b0799)
![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt { 2+{\sqrt {2}}}}{\bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1084c53e1335a7f8522eeaa4df85eae4f09b949)

![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}} \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({ \tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4e94e7593da5994b86a8d00b41d1a995a271de3)

![{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {1}{20}}\pi)\cos ({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e7d8ad6ab6e7245cb9d5c25babd2569853dc19)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\bigl (}{\sqrt {{\sqrt { 5}}+2}}+1{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b34cf55bf836000ca5e342d34a0ec6afea26924)

![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}} \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({ \tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1417b1975f846d4d0b927f839420a78462a5801)





















![{\displaystyle r\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d4a8acea9f5c4e59d8f5fd0ea3c695efa7252fe)

![{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2( 1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm { d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49646481c38b1e3eb1ab582491a98c24fb78c899)

![{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951483e802c58ce9f682e50c2662b425002a37aa)





























































































![{\displaystyle {\text{sl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\ varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\cos ^{2}x}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea0fd8fcd22500f4a1005dc9da044065b9b13891)
![{\displaystyle {\text{cl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\ varpi }}\cos x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\sin ^{2}x}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b7ebedb88c23dbd7dfa5aa905767ab525b63562)





















![{\displaystyle N(z)={\frac {M((1+i)z)}{(1+i)M(z)}},\quad z\notin \varpi \mathbb {Z} [i] }](https://wikimedia.org/api/rest_v1/media/math/render/svg/574d3a65c19e7513f2031d645101f7043784ce55)
































![{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi } 2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb5d4df31aa6a387b048c66646e6f722f3b5f4)
![{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\ bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1 -\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\ Bigr )}\\[7mu]&\quad {}={\frac {2}{2+{\sqrt {7}}+{\sqrt {21+8{\sqrt {7}}}}+{\sqrt {2{14+6{\sqrt {7}}+{\sqrt {455+172{\sqrt {7}}}}}}}}}\\[18mu] &{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi { \bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\[-3mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}={\tan }{\ Biggl (}{\frac {\pi }{4}}-{\arctan }{\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{ 12}}}{\Biggr )}{\Biggr )}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb84aa465ba4cb805b8389f18ca3bc3482ea2b5)







![{\displaystyle \operatorname {aslh} (x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={ \frac {1}{2}}F{\bigl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4450a96a5aea12b8d6f6c62c03d3069521d772)
![{\displaystyle \operatorname {aclh} (x)=\int _{x}^{\infty }{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y= {\frac {1}{2}}F{\bigl [}2\operatorname {arccot}(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4187488347c3b003b4517d3ff8a364a4a4b5ec39)

![{\displaystyle \operatorname {aslh} (x)={\sqrt {2}} \operatorname {arcsl} {\bigl [}x({\sqrt {x^{4}+1}}+1)^{- 1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e31916e0c226f571375b21b813f8d7698f7384f0)
![{\displaystyle \operatorname {arcsl} (x)={\sqrt {2}} \operatorname {aslh} {\bigl [}x(1+{\sqrt {1-x^{4}}})^{- 1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a10b910274a983a4ef695bd0e51357c26e9284a)


![{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {( {\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+ x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f119a40d6612bf47dcb0933374839dd5372e26)





![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt { 2}}\operatorname {arcsl} }{\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d45c585bd9e4ea8c08b7b4a057cec3c98f322bb)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl } {\frac {x}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6942aa471710bbe06a43e659e55a798e1d72023)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname { arcsl} }{\frac {x}{1+{\sqrt {1-x^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45cfc4fa0bf6650e1422d8807eda434011da954)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname { arcsl} }{\frac {x}{{\sqrt {x^{2}+1}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dd004729e1ee0cee73ec93ba8f6d70c47fb019e)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\ frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d352d10b445bbc88a208fc3d9c759830f8d945)



















![{\displaystyle \operatorname {slh} z = {\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}} z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56dd44181c73fe6b48af847f7fb236e52b7816a2)
![{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}] {-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc66d9221d4e85075dc6e4e7eda93fb76745fb63)






![{\displaystyle {\frac {\mathrm {d} {\mathrm {d} u}}\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {slh} ( u)^{2}{\bigr ]}=\operatorname {slh} (u)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e51b6288ac0c7a354ecb3c2868e7553a851c8de8)
![{\displaystyle {\frac {\mathrm {d} {\mathrm {d} u}}-\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {clh} (u)^{2}{\bigr ]}=\operatorname {clh} (u)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/049ec4e8f4e9f40da5061d070f3a5c5d0c662fba)


![{\displaystyle {\text{tlh}}(u)={\frac {{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt [{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{ \tfrac {1}{2}}{\sqrt {2}})^{4}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac149fa68d6fcb0114534181fb5d7e24d78da610)
![{\displaystyle {\text{ctlh}}(u)={\frac {{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt [{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{ \tfrac {1}{2}}{\sqrt {2}})^{4}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a686f87f398e6df8bfc3835f2c39e82473348e0)













![{\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2)} {\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d13d90f0552a5b231cde7c29fcc622ea0c529b6)
![{\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2)} {\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f62bdd6ed9198c38cf475156efcd304aeb75f9)
![{\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[ \operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2} +1]^{1/2}}}=\operatorname {slh} (w)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bb2e7b64a1654bd7915da2f2ee24c36ea102c4d)


![{\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2 }+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/272cd249cacaf1fb7d3d32aa042602b618e4b78d)

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\ mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt { s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^ {4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc65177ebceb89021d3d58fb66b072ba8792393)
![{\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cb551ee1709a503d81e9cec4c2b83f7a555bd67)
![{\displaystyle {\frac {\mathrm {d} {\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4} }}-{\biggl (}{\frac {\mathrm {d} {\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0442203ff4791d46aa1b08d567063c6384a60807)
![{\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}} }{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a38a1d2985a6df92ef7e4a9e6a5e0769401e0d0)
![{\displaystyle {\frac {\mathrm {d} {\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x }}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1} }}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3366b6e0eca62cd33f2e2e9c7c6e4e34383630c)
![{\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[ {4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{- 3/4}={\frac {1}{\sqrt {x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e4816f6d18a3634e785fa8f89e118ba67ab3465)





![{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{ 3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3771b99819f3ade1a833abb09b3fdf307a92bb6)
![{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt { 3}}+3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c26a538dd5ef43ca0c05bec9c37438ebc47fee4b)
![{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{ 2}}}({\sqrt {{\sqrt {2}}+1}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15cd9e1066b6c30c7a5bdbf2b6808844d2f74495)
![{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}] {2}}}({\sqrt {{\sqrt {2}}+1}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d66a35bc4c583c71edf481945e61d079c0d536b)
![{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{ 8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{ 20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87e3cc8738d396091259d97acda2eed94a65c512)
![{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4 }]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{ 20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ed83d6f4ad6eba22ae9e99f2c85c2c4a8145daf)
![{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}] {8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{ 20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af3c2916c1b8aac3a7dffd384036480a0ec32c4a)
![{\displaystyle \operatorname {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4 }]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\ пи )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daba02aa44534c3cc6e7a38c0535f31e75d9ab63)
![{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt { 2{\sqrt {3}}+3}}+1)(1- {\sqrt[{4}]{2{\sqrt {3}}-3}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1235f91589de192f4d5ba4cd436fc5f628ec5a6c)
![{\displaystyle \operatorname {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f98f8f7f5f76843782189dec5e908a7d35c6d6a6)






![{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b95bf2960a1ef78ea3b786b655b45a578835df)


![{\displaystyle -1{\big /}{\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a31b674ac78a5a7b3b44666fc5bb8e646d8de17e)
![{\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}} (x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8332beb95c769a3a02b081fe7cb6952fe061134a)
![{\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}} (x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e792d8ef543c8092c0ebf91002610e1b870ad46)
![{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2 }}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a52e10d08d095a4528b4d3edc8f445388a33fa)
![{\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\, {\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1 )^{-1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcbfa061953d1525d7eceb793ec5b9d4ff3d6786)


![{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x ^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af856ee0c86e4392d104a519e6a3e4e6dedf2196)
![{\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x ^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ed8dda6f6934c99333688d836ecb33384489c9b)
![{\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x ^{4}+1}}+1}}-x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/526683177df0d4b806ad6ea30226bc7286f39846)
![{\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x ^{4}+1}}+1}}+x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92f02c5717e1cef246c52819409059208d17659)
![{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\, {\text{aclh}}(x)]={\text{cl}}[ {\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b544f5a5f0814402638d89811e6be1e665ca5d3)
![{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\, {\text{aslh}}(x)]={\text{cl}}[ {\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]=x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63dce5dab60dff656a75daf045976e8f212d3662)

![{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _ {0}^{\infty }\int _{0}^{\infty }\exp(-y^{2}-z^{2})\,\mathrm {d} y\,\mathrm {d} z=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b51d2740c2198519c7753838241d8bd82ca6b2)
![{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos( \phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9b620bdfd0a0d029022ce5e0e1cce5781d232c)

![{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _ {0}^{\infty }\int _{0}^{\infty }\exp(-y^{4}-z^{4})\,\mathrm {d} y\,\mathrm {d} z=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0742118348484c98e4d359b6a93ac2843fd6349e)
![{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\, \,r\,{\text{ctlh}}(\phi ) &\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi ) &\partial /\partial \phi \,\,r\,{\text{tlh}}( \phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\ ,\mathrm {d} \phi =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6a3f5d46d9ca50219760fdf00282b8c3949165)


















![{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4n}}}=\mathrm {H} _{4n} {\frac {(2\varpi )^{4n}}{(4n)!}}=G_{4n}(i),\quad n\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efdff7133fad5cdcaf38afc18fa194e5029ce05a)

































![{\displaystyle p'\in \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3159bf62df44731a1592ff4d718a9b988b83f6ab)




















































